Mathematica 數學軟件與函數極限和導數教學

王景艷 李凱敏

（保山學院數學學院 云南·保山 678000）

本文主要借助高等數學教材，討論Mathematica數學軟件輔助高等數學函數極限和導數教學的研究，主要研究一元和二元函數的極限及一元函數的導數和二元函數的偏導數，通過Mathematica數學軟件的簡單實例教學，提高教學效率和學生學習高等數學的積極性。

1 一元函數極限的實例教學

極限在高等數學中占非常重要的位置，是高等數學的理論基礎，高等數學里的很多內容都和極限有關，比如說連續、導數和定積分，所以學生們學好函數極限是非常重要的。因此，借助Mathematica 數學軟件的符號計算功能，讓學生很好的理解和掌握極限，為后續課程內容打下基礎。

解：分別求它們的數值解，因為它們都是偶函數，所以 的值只取正的，輸入輸出分別如下：

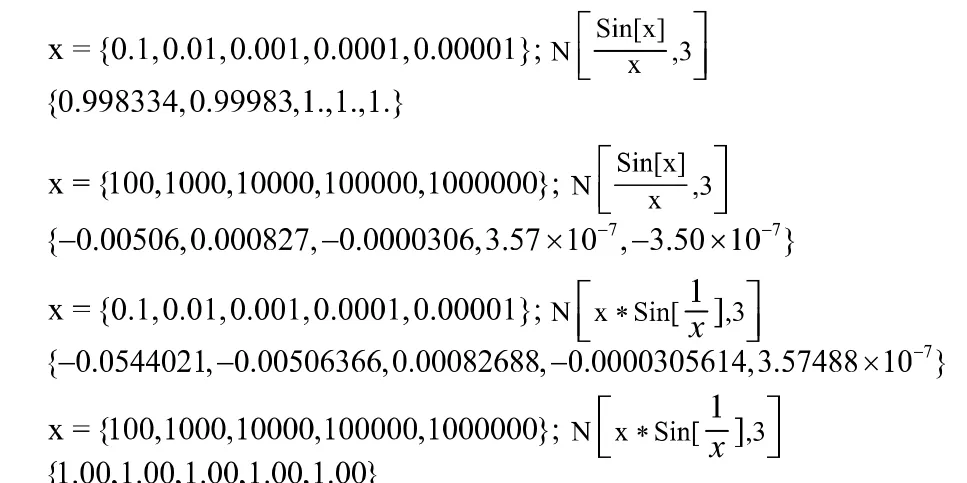
輸出：如圖1 所示。

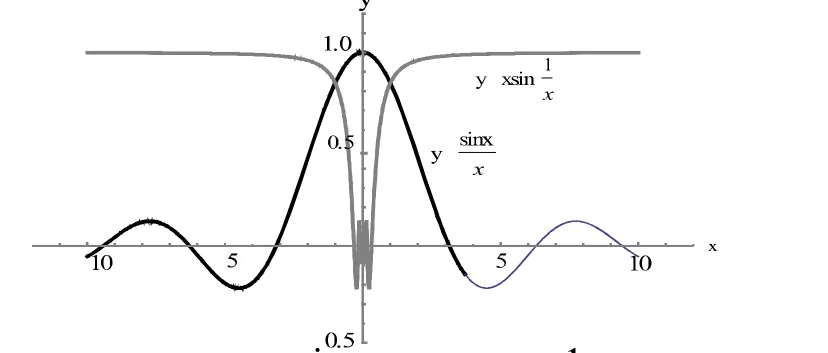
圖1 函數的圖形

2 二元函數極限的實例教學

二元函數與一元函數的極限定義和求解是相似的，但二元函數的極限比一元函數的極限要復雜些。

3 一元函數導數及其應用的實例教學

導數是高等數學中重要的基礎概念，在高等數學中占有重要位置。學生們往往記不住導數公式，或是在求導過程中不注重方法。

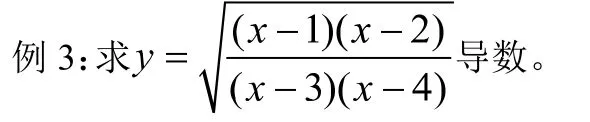
分析：這個題如果不注重求導的方法和化簡，那么過程繁瑣，計算量大，但學生往往忘記了對數求導法，直接求解，但不知道結果是否正確。那么通過 Mathematica 數學軟件的多項式運算，對其化簡，分項，通分，輸入輸出：

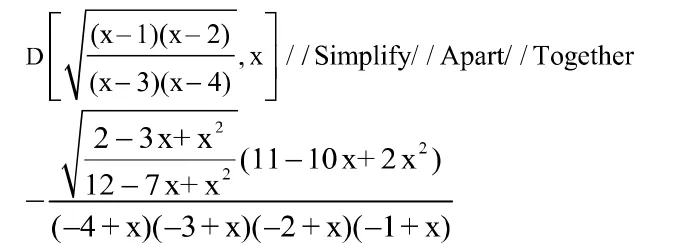
但這個題最簡單的方法是對數求導法，但結果形式上不一樣，那么是不是對的呢？可以進行驗證，把對數求導法的結果進行通分，故輸入輸出：

4 二元函數偏導數及其應用的實例教學

二元函數的偏導數往往比一元函數的導數復雜，因為它有兩個自變量，學生在學習和求解中出現畏難情緒，有時求解出來了，但不知道對不對，還有些函數看似簡單，但求解復雜，因此借助Mathematica 數學軟件的符號計算功能，可以求解，并進行驗證。

分析：先求一階偏導，再求二階偏導，Mathematica 數學軟件求偏導數的命令和一元函數的類似，輸入輸出，有

還可以演示求解更高階導數的偏導數，來激發學生的學習積極性。

5 結論

本文主要探討了 Mathematica 數學軟件輔助一元和二元函數的極限及一元函數的導數和二元函數的偏導數及其應用的幾個典型實例。那么在實際教學中，還可以不斷的研究和改進命令，不斷的實驗，不僅幫助學生掌握知識和發現規律，提高教學效率，還可以提高學生學習高等數學的積極性，培養他們自主學習的良好習慣。