一類非線性波動(dòng)方程的孤波解

楊 潔， 肖 冰， 張 寧

（新疆師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院，烏魯木齊 830017）

隨著科學(xué)技術(shù)的發(fā)展，越來越多的復(fù)雜問題都可以用非線性偏微分方程來描述，例如在流體力學(xué)、等離子物理學(xué)、光電通信、固態(tài)物理學(xué)以及交通等領(lǐng)域應(yīng)用廣泛. 但是由于線性微分方程的一些基本性質(zhì)在非線性微分方程中不再成立，很難用一個(gè)統(tǒng)一的方法來求解后者，所以長(zhǎng)期以來，求解非線性偏微分方程的精確解一直是數(shù)學(xué)家和物理學(xué)家研究的熱點(diǎn)問題［1-3］.

目前已發(fā)現(xiàn)越來越多的具有重要物理意義的非線性偏微分方程，如Korteweg-deVries方程、Huxley方程、Fitzhugh-Nagumo方程等都具有各種類型的孤立波解［4-5］. 孤立子正在流體物理學(xué)、基本粒子物理學(xué)、生物醫(yī)學(xué)等許多領(lǐng)域找到了應(yīng)用，并對(duì)一些過去難以解釋的現(xiàn)象做了說明. 隨著孤立子理論的發(fā)展，人們提出了許多求解非線性偏微分方程的有效方法，如齊次平衡法［6］、G/G′展開法［7］、雙曲正切函數(shù)展開法［8］、Jacobi橢圓函數(shù)展開法［9］、試探函數(shù)法［10］等一系列的方法.

最近，王明亮等［11］用齊次平衡法求出了一個(gè)1+1維非線性波動(dòng)方程

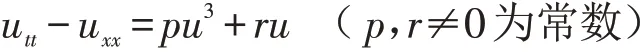
的精確解. 張衛(wèi)國(guó)［12］用待定系數(shù)法求出了非線性波動(dòng)方程

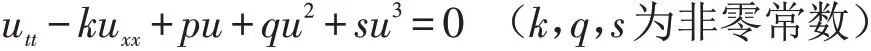
的鐘狀和扭狀孤波解. 范恩貴等［13］用齊次平衡法求出了一類非線性波動(dòng)方程

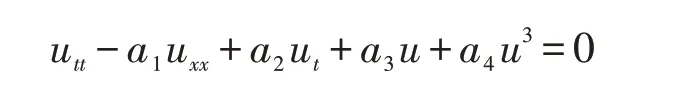
的孤立波解. 尚亞東［14］用結(jié)合假設(shè)方法求出了非線性波動(dòng)方程

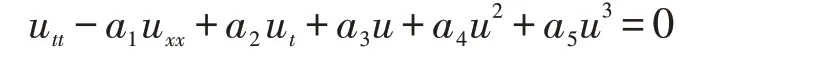
的一些顯式精確行波解.

基于他們的研究，本文利用最近引入的首次積分法的思想［15-16］，來求解如下一類應(yīng)用較廣泛的非線性波動(dòng)方程

的孤波解，其中a1，a2，a3，a4，a5均……