NORM STRUCTURES OF A FUZZY NORMED SPACE

LI Xin-xin,WU Jian-rong

(School of Mathematics and Physics,Suzhou University of Science and Technology,Suzhou 215009,China)

Abstract:In this paper,the problem of norm structures in the fuzzy normed space is studied.By using the ”cut” method and introducing K function,we discuss the norm structures existing in the fuzzy normed space with continuous t-norm in a broader sense,and give the relations between these norm structures.The obtained results generalize the existing conclusions and provide a new way for the further research of the fuzzy normed space.

Keywords:fuzzy analysis;fuzzy normed space;norm structure;topology

1 Introduction

Inspired by the notion of probabilistic metric spaces,Kramosil and Michalek[1]in 1975 introduced the notion of fuzzy metric,a fuzzy set in the Cartesian productX×X×(-∞+∞)satisfying certain conditions.Later,George and Veeramani[2]used the concept of continuoust-norm to modify this definition of fuzzy metric space and showed that every fuzzy metric space generates a Hausdorff first countable topology.In 1994,Cheng and Mordeson[3]introduced an idea of a fuzzy norm on a linear space in such a manner that the corresponding fuzzy metric is of Kramosil and Michalek type[1].Following Cheng and Mordeson,Bag and Samanta[4]introduced a similar definition of fuzzy norm.The novelty of this definition is the validity of a decomposition theorem for a special type of fuzzy norm into a family of crisp norms.This concept was used in fuzzy functional analysis and its applications[5–8].In[9],Sadeqi and Kia proved that a separating family of seminorms introduces a fuzzy norm in general but it is not true in classical analysis.In[10],Alegre and Romaguera also dealt with fuzzy normed spaces in the sense of[3],characterized fuzzy norms in terms of a nondecreasing and separating family of seminorms,and generalized the classical Hahn-Banach extension theorem for normed spaces.In addition to this,Bag and Samanta established some principles of functional analysis in fuzzy settings,which represent a foundation for the development of fuzzy functional analysis.Some other conclusions can be found in[11–16].

In this paper,we introduce the concept ofr-norm and show some norm structures in a fuzzy normed space.Moreover,we investigate the relationships between the normed topology and the topology induced by these norm structures.The structure of the paper is as follows.In the next section,we give the preliminaries on a fuzzy normed space.In Section 3,we show our main results.

In this paper,Ris the set of all real numbers,R+is the set of all positive real numbers,Xis a real linear space.

2 Preliminaries

In this section,we first recall some basic concepts of fuzzy normed spaces.

definition 2.1(see[17])A binary operation*:[0,1]×[0,1]→[0,1]is a continuoust-norm,if*satisfies the following conditions:?a,b,c,d∈[0,1],

(1)commutativea*b=b*a;

(2)associative(a*b)*c=a*(b*c);

(3)a*b≤c*dwhenevera≤candb≤d;

(4)a*1=a;

(5)*is continuous.

Lemma 2.1(see[17])Let*:[0,1]×[0,1]→[0,1]be a continuoust-norm.

(1)If 1＞r1＞r2＞0,then there existsr3∈(0,1)such thatr1*r3≥r2;

(2)Ifr4∈(0,1),then there existsr5∈(0,1)such thatr5*r5≥r4.

We can strengthen Lemma 2.1 to the following form.

Lemma 2.2Let*:[0,1]×[0,1]→[0,1]be a continuoust-norm.

(1)If 1＞r1＞r2＞0,then there existsr3∈(0,1)such thatr1*r3＞r2;

(2)Ifr4∈(0,1),then there existsr5∈(r4,1),such thatr5*r5＞r4.

Proof(1)Let 1＞r1＞r2＞0.Taker∈(r2,r1).From Lemma 2.1(1),there existsr3∈(0,1)such thatr1*r3≥r.Thusr1*r3＞r2.

(2)Letr4∈(0,1).Taker∈(r4,1).From Lemma 2.1(2),there existsr5∈(0,1)such thatr5*r5≥r.Thusr5*r5＞r4.

In this paper,the definition of a fuzzy normed linear space in[4]is changed accordingly,and the following definition is given.

definition 2.2LetXbe a linear space,*be a continuoust-norm,Nbe a fuzzy subset ofX×(0,+∞).Nis called a fuzzy norm onXif the following conditions are satisfied:for allx,y∈X,

(1)?t＞0,N(x,t)＞0;

(2)(?t＞0 ,N(x,t)=1)iffx=θ,whereθis the zero element ofX;

(3)?t＞0 ,

(4)?t,s＞0,N(x,t)*N(y,s)≤N(x+y,t+s);

(5)N(x,·):(0+∞)→( 0,1]is continuous.

The 3-tuple(X,N,*)is said to be a fuzzy normed linear space.Obviously,ifNis a fuzzy norm,thenN(x,·)is non-decreasing for allx∈X.

Remark 2.1If(1)and(5)are replaced by

(N1)?t∈Rwitht≤0 ,N(x,t)=0;

(N5)N(x,·)is a non-decreasing function ofRandrespectively,thenNis a fuzzy norm in the sense of[4].

Example 2.1LetXbe a linear normed space,N:X×(0,+∞)→(0,1]is defined bythenNis a fuzzy norm onX.

In the rest of this paper,we always suppose the functionK:[0,1]→[0,1]satisfies the following conditions:K(0)=0,K(t)/≡0,Kis increasing and continuous at 0.

Theorem 2.1Let(X,N,*)be a fuzzy normed linear space.Forx∈X,r∈(0,1),t＞0,we define

Then{BN(x,r,t):r∈(0,1),t＞0}is a base of neighborhoods atx.

Proof(1)?x∈X,t＞0,r∈(0,1),x∈BN(x,r,t).

(2)?x∈X,0＜r1,r2＜1,t1,t2＞0,there existsr3=min{r1,r2},t3={t1,t2},from the non-decreasing ofN(x,·),we haveBN(x,r3,t3)?BN(x,r2,t2),BN(x,r3,t3)?BN(x,r1,t1),soBN(x,r3,t3)?BN(x,r2,t2)∩BN(x,r1,t1).

(3)For anyBN(x,r,t),from Lemma 2.2,we have 0＜r1＜rsuch that(1-K(r1))*(1-K(r1))＞1-K(r).Lety∈BN(x,r1,t)?BN(x,r,t),we knowN(x-y,t)+K(r1)＞1.SinceN(x-y,·)is continuous,we can takeδ＞0 such thatN(x-y,t-δ)+K(r1)＞1 .Therefore,for anyz∈BN(y,r1,δ),we haveN(y-z,δ)+K(r1)＞1 and

Thus,z∈BN(x,r,t).From the arbitrariness ofz,we knowBN(y,r1,δ)?BN(x,r,t).From(1)–(3),we can conclude that{BN(x,r,t):x∈X,r∈( 0,1),t＞0}forms a base of neighborhoods atx∈X.

Based on the{BN(x,r,t):x∈X,r∈( 0,1),t＞0},we have a topologyτNwhich is said to be the topology generated by the fuzzy normN.It is easy to see the topologyτNis the first countable.In fact,the countable collection of balls{BN(x,1/n,1/n):x∈X,n=2,3,...}forms a base of neighborhoods atx∈X.

3 Main Results

In this section,we shall introduce norm structures in a fuzzy normed space,and investigate the relationships between the fuzzy topologyτNand the topologies induced by these norm structures.For simplicity,we always suppose a fuzzy normed space(X,N,*)satisfies the regular condition:?x∈X,there existst＞0 such thatN(x,t)=1.

Theorem 3.1Let(X,N,*)be a fuzzy normed space.define a function‖·‖0onXas follows

then‖·‖0is a norm onX.

ProofObviously,for allx∈X,‖x‖0≥0 ,‖x‖0=0 if and only ifx=θ.Now,for anyx,y∈X,ε＞0 ,from the definition of‖·‖0,we get that

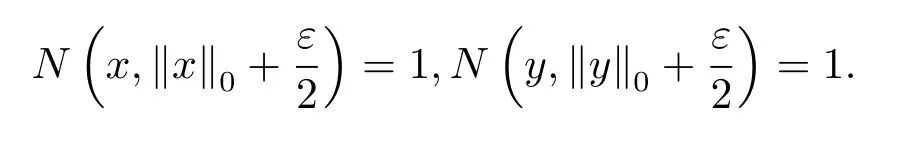
Therefore

and hence‖x+y‖0≤‖x‖0+‖y‖0+ε.From the arbitrariness ofε＞0 ,we have

Additionally,?α∈R{0},we have

Obviously,‖αx‖0=|α|‖x‖0ifα= 0.Thus‖·‖0is a norm onX.

Theorem 3.2(X,N,*)is a fuzzy normed space,‖·‖0is the norm defined by(3.1).Letr∈(0,1],x∈X,

Then,for a fixed pointx∈X,‖x‖ris a decreasing function with respect tor∈( 0,1],and

ProofGivenx∈X,r1,r2∈(0,1)withr1≥r2,we have

hence‖x‖r1≤‖x‖r2,which means‖x‖ris decreasing with respect tor∈( 0,1].Soexists and

Moreover,for anyε＞0 ,x∈X,N(x,‖x‖0+ε)=1.From(3.2),we obtain

From the arbitrariness ofε＞0 ,we know

On the other hand,for anyε＞0 ,we knowt＞‖x‖0-εwheneverN(x,t)=1 from the definition of‖·‖0.That is,N(x,t)＜1 on(0,‖x‖0-ε].Recalling thatKis increasing and continuous at 0,there existsr0=r0(ε)such thatN(x,t)+K(r0)＜1 on(0,‖x‖0-ε].That is,t＞‖x‖0-εwheneverN(x,t)+K(r0)≥1.Then we have

which together with the arbitrariness ofεimplies that

Inequalities(3.4)and(3.5)imply the equation(3.3).

Remark 3.1In[4],‖x‖rwas defined as inf{t＞0:N(x,t)≥r}.Therefore,the definition(3.2)of‖x‖ris a generalization of that in[4].We call‖·‖rther-norm in a fuzzy normed space(X,N,*).

Lemma 3.1Let(X,N,*)be a fuzzy normed space,x∈X.IfN(x,·)is strictly increasing,then

ProofFor anyr∈(0,1),lett0=inf{t＞0:N(x,t)+K(r)＞1}.From(3.2),we get‖x‖r≤t0.If‖x‖r＜t0,then there is 0＜t2＜t0such thatN(x,t2)+K(r)≥1.SinceN(x,·)is strictly increasing,thenN(x,t0)+K(r)＞1.From the continuity ofN(x,·),there isδ＞0 such thatN(x,t0-δ)+K(r)＞1 which conflicts with the definition oft0.Thus,‖x‖r=t0=inf{t＞0:N(x,t)+K(r)＞1}.

Lemma 3.2(X,N,*)is a fuzzy normed space.N(x,·)is strictly increasing for the fixed pointx∈X.Lett＞0 andr∈(0,1).Then‖x-y‖r＜tif and only ifN(x-y,t)+K(r)＞1,that isBN(x,r,t)=Nr(x,t),where

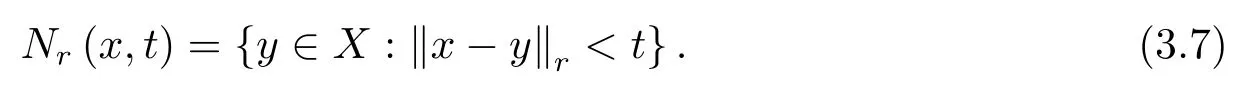
ProofSuppose‖x-y‖r＜t.From Lemma 3.1,there exists 0＜t0＜tsuch thatN(x-y,t0)+K(r)＞1.Hence,N(x-y,t)+K(r)＞N(x-y,t0)+K(r)＞1.SoBN(x,r,t)?Nr(x,t).

Now,we supposeN(x-y,t)+K(r)＞1.SinceN(x-y,·)is continuous,there exists 0＜t1＜tsuch thatN(x-y,t1)+K(r)＞1.From(3.6),we know‖x-y‖r≤t1＜t.SoBN(x,r,t)?Nr(x,t).This completes the proof.

Theorem 3.3(X,N,*)is a fuzzy normed space,N(x,·)is strictly increasing for the fixed pointx∈X.Then‖x‖r=‖x‖0forr∈(0,1]if and only ifNsatisfies the following condition:for allt＞0,

ProofThe sufficiency is obvious.

To prove the necessity,we suppose that‖x‖r=‖x‖0andN(x,t)+K(r)＞1.From the definition of‖x‖r,‖x‖r≤t,that is‖x‖0≤t.For anyε＞0,from the definition of‖·‖0,we gett′＞0 such thatt+ε＞t′andN(x,t′)=1.Therefore,N(x,t+ε)=1,which together with the continuity ofN(x,·)implies thatN(x,t)=1.

Theorem 3.4If(X,N,*)is a fuzzy normed space,then

(i)the topologyτ0generated by‖·‖0is stronger than the topologyτN;

(ii)τ0=τNif and only ifNsatisfies the following condition:for eachx∈X,t＞0 andy∈N0(x,t),there existr′∈(0,1),t′＞0 and 0＜s′＜tsuch that

where

Proof(i)To proveτ0?τN,it is sufficient to prove{xn}is convergent tox0with respect toτNwhenever{xn}is convergent tox0with respect toτ0.In fact,if{xn}is convergent tox0with respect toτ0,then for anyε＞0,there existsNsuch thatfor alln≥N.Therefore,for anyr∈(0,1],we have‖xn-x0‖r＜εfor alln≥N.From Lemma 3.2,we haveN(xn-x0,ε)+K(r)＞1 for alln≥N.That is,xn∈BN(x0,r,ε)for alln≥N.Thus,{xn}is convergent tox0with respect toτN.

(ii)NecessityWe suppose thatτ0=τN.Then,for eachx∈Xandt＞0,N0(x,t)∈τ0?τN. Hence,for eachy∈N0(x,t),there existr′∈(0,1)andt′＞0 such thatBN(y,r′,t′)?N0(x,t),that is,‖x-z‖0＜twheneverN(y-z,t′)+K(r′)＞1 for anyz∈X.Obviously,‖x-z‖0＜tis equivalent to that there exists 0＜s′＜tsuch thatN(x-z,s′)=1.

SufficiencyFrom(i),we only have to proveτ0?τN.To do that,it is sufficient to proveN0(x,t)∈τNfor eachx∈X,t＞0.In fact,for anyy∈N0(x,t),by the supposition,there existr′∈(0,1),t′＞0 and 0＜s′＜tsuch that(3.9)holds,Which means thatBN(y,r′,t′)?N0(x,t).ThusN0(x,t)∈τN.

Corollary 3.1(X,N,*)is a fuzzy normed space.N(x,·)is strictly increasing for the fixed pointx∈X.IfNsatisfies the following condition:there existsr′∈(0,1)such that for anyt＞0,x∈X,

Thenτ0=τN.

ProofLetx∈X,t＞0 andy∈N0(x,t)arbitrarily,by the definition ofN0(x,t),there exists 0＜s*＜tsuch thatN(x-y,s*)=1.Takes*＜s′＜t,t′=s′-s*.By the supposition,whenN(z-y,t′)+K(r′)＞1,we haveN(z-y,t′)=1,and hence

From Theorem 3.4(ii),we knowτ0=τN.

Theorem 3.5(X,N,*)is a fuzzy normed space,N(x,·)is strictly increasing for the fixed pointx∈X.‖·‖ris defined by(3.2)for anyr∈(0,1).Then‖·‖ris a pseudonorm onXif and only ifNsatisfies the following condition:for anyx,y∈X,t1,t2＞0,N(x-z,t1)+K(r)＞1 andN(z-y,t2)+K(r)＞1 imply thatN(x-y,t1+t2)+K(r)＞1.

Proof SufficiencyIt is easy to see that‖x‖r≥0,‖x‖r=0 ifx=θ.

For anyε＞0,we obtain

By the supposition,we obtain

Therefore

From the arbitrariness ofε＞0,we know

Now,we prove‖αx‖r=|α|‖x‖r.In fact,?α∈R{0},we have

Obviously,‖αx‖r=|α|‖x‖rifα=0.

NecessitySuppose thatN(x-z,t1)+K(r)＞1 andN(z-y,t2)+K(r)＞1.By the continuity ofN(x,·),there existsδ＞0 such thatN(x-z,t1-δ)+K(r)＞1 andN(z-y,t2-δ)+K(r)＞1.So‖x-z‖r≤t1-δand‖z-y‖r≤t2-δ.Since‖x-y‖r≤‖x-z‖r+‖z-y‖r,we have‖x-y‖r≤t1+t2-2δ＜t1+t2.By(3.2),there existst0＜t1+t2such thatN(x-y,t0)+K(r)≥1.SinceN(x-y,·)is strictly increasing,we getN(x-y,t1+t2)+K(r)＞1.