基于魯棒H∞控制的多機協同編隊

王 平，羅 陽，于均杰

(海鷹航空通用裝備有限責任公司，北京 100074)

0 引言

近年來,多無人機系統的協同編隊控制問題受到廣泛關注。多機協同能夠充分發揮單機的功能、提高任務的完成率、拓寬使用范圍等[1]，在民生和軍事等領域均具有巨大的應用潛力。編隊保持作為協同編隊控制方面的基本問題，是編隊有效執行任務的基本保障。在協同偵察和協同定位等任務中，由于載荷特性對無人機編隊保持和相對位置精度提出了較高的要求。然而,在大氣環境中環境風會對編隊隊形的保持產生很大的干擾，并且相比有人機等大飛機，無人機普遍體型較小、抗風干擾能力差。因此，風干擾情況下提高無人機協同編隊的保持精度成為亟待解決的問題。

目前，編隊保持和控制的方法主要包括領航-跟隨法[2]、虛擬結構法[3]、行為控制法[4]以及一致性控制方法[5-6]。Ren在文獻[7]中論證了領航-跟隨法、虛擬結構法以及行為控制法都可以歸入一致性的統一框架內。現有的無人機編隊控制研究主要集中在通信時滯和控制受限等情況下的編隊保持問題。針對干擾情況下的無人機編隊保持，侯海平等[8]基于領航-跟隨法提出了一種高階滑模編隊控制方法，克服了未知干擾的影響；王曉燕等[9]基于領航-跟隨法設計了無人機編隊魯棒控制器，克服了模型不確定性與外部干擾的影響；Islam等[10]考慮多無人機系統模型存在的非線性和不確定性，依據鄰域位置信號，提出了一種基于分布式一致性的魯棒自適應控制方法。針對風干擾的情況，Wu等[11]研究了風干擾下長僚機編隊的軌跡跟蹤控制方法，利用反步法結合干擾觀測器實現軌跡跟蹤控制；陳俠等[12]針對風干擾下多無人機編隊的航跡跟蹤問題，提出了一種基于Kalman濾波的一致性跟蹤算法;Kukreti等[13]針對風干擾下的軌跡跟蹤,提出了一種遺傳最優的無人機導航算法；Zhang等[14]針對風干擾下多旋翼無人機的時變編隊，設計了一種一致性協議，并通過試驗驗證了其有效性。

在上述研究的基礎上，本文針對環境風干擾情況下無人機編隊保持精度差的問題，設計了基于鄰居無人機相對狀態的編隊保持控制協議。通過選取適當的被控輸出來量化環境風干擾對固定翼多機編隊的影響，將受擾多機編隊控制問題轉化為魯棒H∞控制問題。對于僚機之間通信拓撲為有向圖和無向圖的兩種情形，均以線性矩陣不等式的形式給出滿足期望H∞干擾抑制指標的多機編隊條件，控制參數求解簡單。仿真結果表明，該方法能夠有效提高多機協同編隊的魯棒性，抑制風干擾對編隊保持的影響。

1 編隊的通信拓撲

采用拓撲圖來表示無人機群之間的通信關系，將每架無人機看作拓撲圖中的一個節點，將無人機之間的信息交互看作拓撲圖的邊。

顯然L=D-A。基于長機無鄰居這一事實，可將Laplacian矩陣L寫成如下分塊矩陣的形式

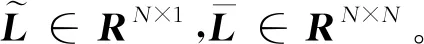
2 無人機編隊數學模型

2.1 2個常用坐標系

多無人機編隊運動需要以坐標系為參考標準，選取適當的坐標系可以更加方便地描述無人機的運動情況，常用的坐標系有如下兩種：

1)大地坐標系

大地坐標系是固定在地球表面的一種坐標系。在地面上任意選取一點作為坐標原點O，Ox軸指向北，Oy軸指向東，Oz軸鉛垂向下。

2)航跡坐標系

航跡坐標系是描述無人機編隊飛行的基礎。選取無人機質心為原點O′，與飛行速度V重合的方向為O′x′軸，與O′x′軸在同一水平平面且垂直于O′x′軸的方向為O′y′軸，O′z′垂直于O′x′y′平面，且滿足右手法則。

2.2 隊形的幾何描述

以正五邊形編隊為例給出無人機編隊的表示方法，如圖1所示。假設無人機已組成預期編隊，Δi,Δj分別表示第i架無人機和第j架無人機相對于長機的距離差向量，ξ0、ξi、ξj分別為虛擬長機，第i架無人機和第j架無人機的位置，它們之間的關系如下：ξi=ξ0+Δi，ξj=ξ0+Δj。

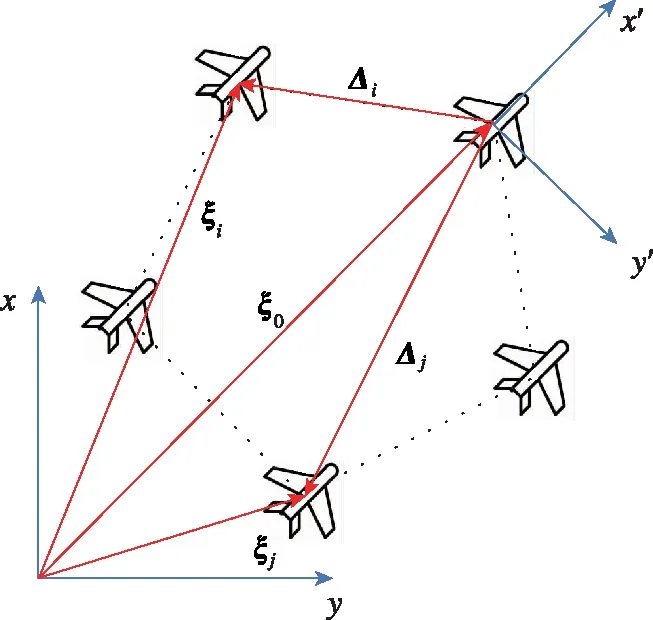
圖1 編隊的表示方法Fig.1 Formation representation

2.3 無人機動力學模型

假設無人機無側滑飛行且不受地球曲率影響，編隊中第i架無人機的三維質點模型為

(1)

其中，g為重力加速度；Vi、χi、γi分別為無人機i的線速度、航跡傾斜角和航跡方位角；di=[d1i,d2i,d3i]T為無人機i受到的風干擾；a1i、a2i、a3i分別為無人機i的切向加速度、法向加速度的水平分量和法向加速度的垂直分量。

3 無人機編隊控制器設計

3.1 模型轉化

記ξi=[xi,yi,zi]T為無人機i在三維空間中的慣性位置，ai=[a1i,a2i,a3i]T為控制輸入，則

(2)

其中

則系統(2)可以簡寫為

(3)

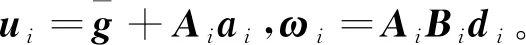
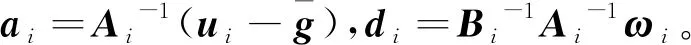
3.2 問題轉化

本文研究了系統(3)的編隊控制問題，即設計了分布式控制協議ui，使得系統中所有無人機形成期望編隊。也就是說

(4)

其中，ξi、ζi分別為第i架無人機的位置和速度狀態；ξ0、ζ0分別為長機的位置和速度狀態；Δi、Rgklead(Δi)k分別表示第i架無人機相對于長機在航跡坐標系和大地坐標系下的位移。

(5)

因此，多無人機系統對風干擾的衰減抑制能力，可由從風干擾ω到被控輸出z的閉環傳遞函數矩陣的H∞范數進行度量，其定義為

(6)

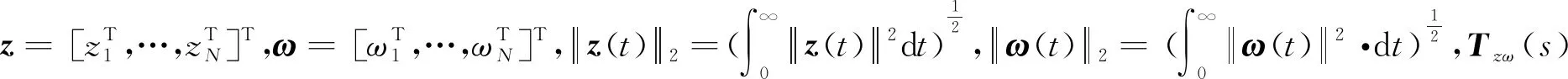
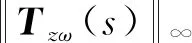
至此，風干擾的無人機系統的編隊控制問題就轉化為H∞控制問題。

3.3 控制協議設計

為解決上述的H∞控制問題，設計如下無人機編隊控制協議

Rgklead(Δj)k)+ai0(ξi-Rgklead(Δi)k-ξ0)]-

(7)

其中，k1,k2>0為待定的反饋增益。

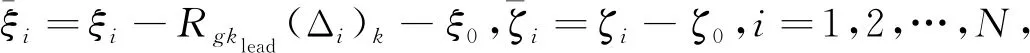
(8)

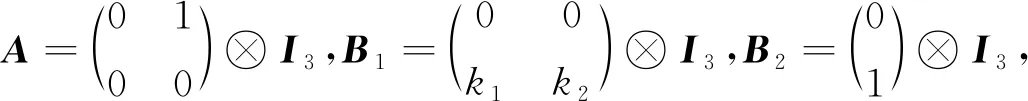
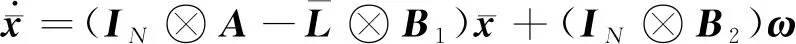
(9)

3.4 多無人機H∞編隊條件

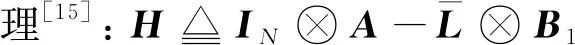
(10)

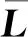
定理：若控制增益k1、k2滿足式(10)，并且存在正定矩陣P∈R6N×6N滿足

(11)

證明：考慮如下的Lyapunov函數

(12)

其中，P∈R6N×6N是正定矩陣。

首先，在沒有外界干擾的情況下，討論系統(9)的穩定性問題。對V(t)求導可得

(13)

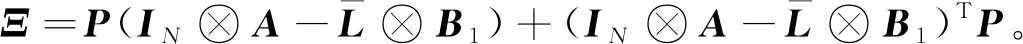
其次，在干擾ω(t)非零情況下，討論系統(9)的魯棒H∞性能。與上述穩定性分析類似，得到

(14)

其中

對任意的T>0，考慮下列代價函數

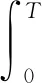
(15)

在零初始條件下，此時V(0)=0，有

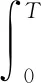
(16)

其中,Ψ=Θ+diag{I6N,-γ2I3N}。

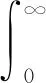
對于僚機之間的通信拓撲圖為無向圖的情形，給出下面的推論。

推論：若控制增益k1、k2滿足式(10)，并且存在正定矩陣P∈R6×6滿足

(17)

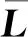
4 仿真實例

本節以1架長機和4架僚機組成的正五邊形平面編隊突遇陣風為例，通過仿真分析，驗證所提出的方法。

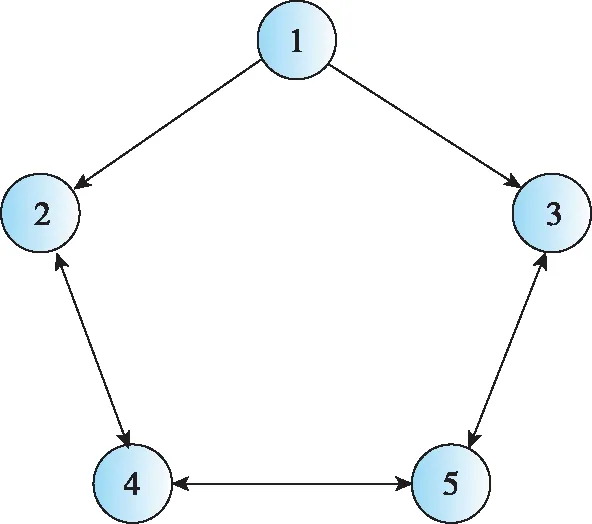
圖2 通信拓撲Fig.2 Communication topology

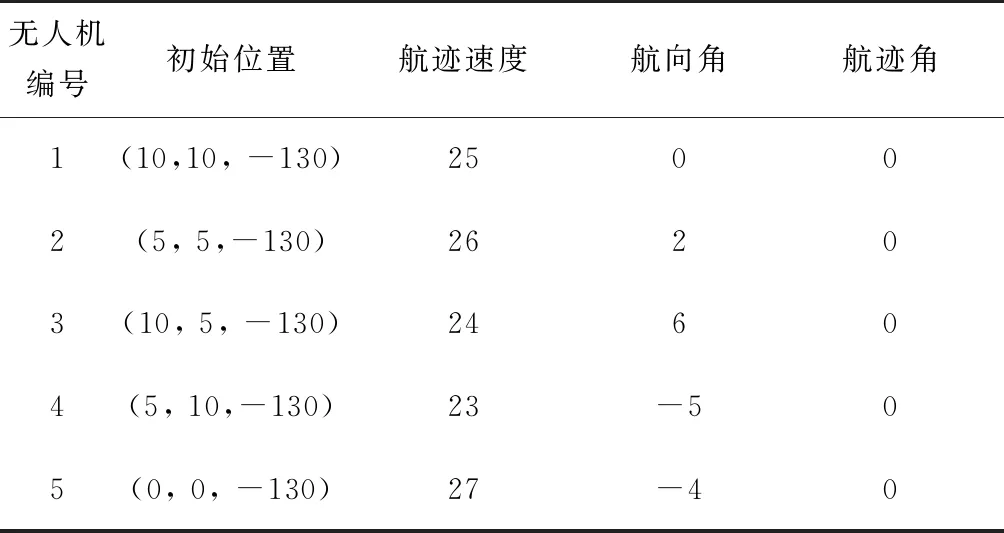
表1 無人機初始狀態信息

本文采用三維質點模型，考慮到無人機的實際機動能力，在仿真過程中對控制量a1i、a2i、a3i進行了限幅

a1i∈[-0.5g,g];

a2i∈[-tan(80°)g,tan(80°)g];

a3i∈[-2g,1.5g]

以1號長機為原點，航跡坐標系為參考坐標系，設置2～5號僚機在長機坐標系中的期望相對位置為

仿真步長為0.01s，在100s時施加持續ΔT=5s的陣風干擾模擬對編隊的影響，陣風干擾的模型如下

(18)

其中，t∈[0,ΔT)為陣風持續的時間。圖 3所示為仿真過程中僚機相對長機的位置變化；圖 4、圖5和圖6分別為X軸、Y軸、Z軸3個方向的相對位置變化在95～150s時間內的局部放大圖；圖 7所示為t1= 105s,t2=115s,t3=150s這3個時刻所保持的編隊隊形。

圖3 在長機坐標系下的相對位置Fig.3 Relative positions in the leader’s coordinate

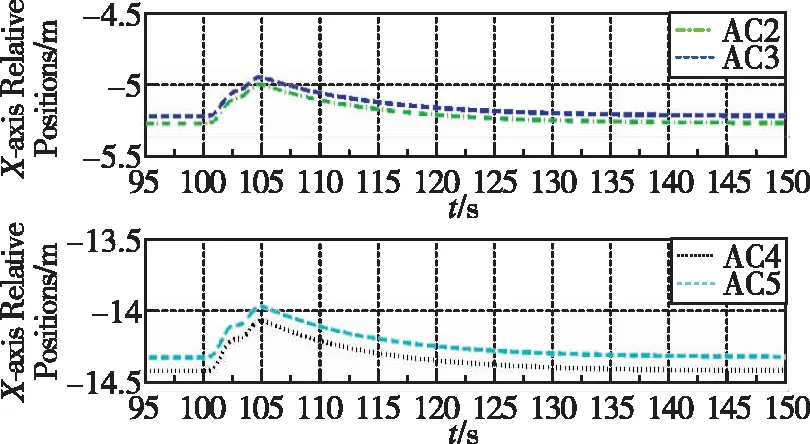
圖4 X軸方向相對位置Fig.4 X-axis relative positions

圖5 Y軸方向相對位置Fig.5 Y-axis relative positions

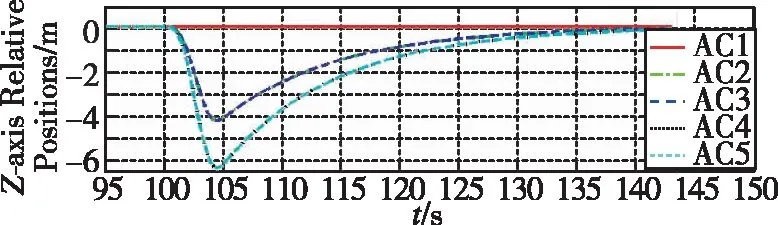
圖6 Z軸方向相對位置Fig.6 Z-axis relative positions

圖7 編隊隊形(t1= 105s, t2=115s, t3=150s)Fig.7 Formation patterns(t1= 105s, t2=115s, t3=150s)

5 結論

本文針對環境風干擾情況下無人機編隊保持精度差的問題，設計了基于鄰居無人機相對狀態的編隊控制協議。理論分析與仿真結果表明：

1)采用一致性編隊控制方法，避免了領航-跟隨法缺少隊形反饋、不適合大規模編隊的問題，擴展性更強；

2)以線性矩陣不等式的形式給出了滿足期望抑制指標的多機編隊條件，對于僚機之間的通信拓撲圖為無向圖的情形，僅通過求解2個線性不等式確定控制協議，控制參數求解簡單、可離線計算，并且不需要單獨設計各通道。

3)本文所提方法能夠有效提高多機協同編隊的魯棒性，抑制風干擾對編隊保持的影響。