基于夜間燈光數據的中國城市電力消費模擬影響因素

張莉，謝亞楠，屈辰陽，汪鳴泉，王茂華

(1.上海大學 特種光纖與光接入網重點實驗室，上海 201210；2.中國科學院上海高等研究院 上海碳數據與碳評估中心，上海 201210；3.中國科學院低碳轉化科學與工程重點實驗室，上海 201210)

0 引言

電力是現代社會發展不可或缺的數據源，是反映經濟走勢的重要風向標。而電力消費也是經濟發展的先行指標[1]。及時準確地估算城市電力消費量(electric power consumption，EPC)，對于合理制定發展政策、調配電力資源具有重要意義。傳統EPC數據通過每年統計獲得，其更新速度慢，存在數據缺失等缺點，制約了該數據的實用性發展。

美國國防氣象衛星(defense meteorological satellite program，DMSP)搭載的業務型線掃描傳感器(operational linescan system，OLS)和美國新一代Suomi對地觀測衛星(national polar-orbiting partnership，NPP)搭載的可見光紅外成像輻射儀(visible infrared imaging radiometer suite，VIIRS)能夠記錄城市的低強度夜間燈光，數據更新時間快，可以作為檢測城市電力消費量的理想數據源[2]。NOAA在其官網發布了1992—2013年DMSP-OLS衛星年度穩定夜間燈光(nighttime light，NTL)影像以及2013—2018年NPP-VIIRS衛星月度穩定NTL影像。2種衛星影像都記錄了2013年的夜間燈光。

自20世紀80年代以來，國內外學者對利用DMSP-OLS和NPP-VIIRS衛星NTL影像進行包括EPC在內的各種社會經濟參量的模擬開展了大量的研究[2-3]。結果顯示，在國家[4-6]、省份[1，6-8]、城市[9-11]甚至更小尺度[12-16]使用線性模型[9-10]，對數模型[1，4，6，14]以及二次[5]回歸模型進行模擬，NTL與EPC均表現出良好的相關性。其中，對數模型是當前最常使用的模型。自1997年，Elvidge等[4]以21個國家為研究對象，建立了DMSP-OLS夜間燈光與電力消費量(NTL-EPC)的對數模型后，文獻[7，15]分別建立了中國省級和縣級尺度的NTL-EPC對數模型。

為減小模擬誤差，有學者建立了更為復雜的模型：馬忠玉等[1]構建了加入地理時空模型的NTL-EPC對數模型，利用DMSP-OLS衛星NTL影像，對中國省級EPC關系模擬，并取得了很好的效果，但該模型復雜度高，不適用于中國城市層面的研究。有學者通過控制城市范圍，減小DMSP-OLS衛星對微弱燈光不敏感帶來的誤差：Xie等[17]通過閾值法提取城市區域的NTL，對EPC進行模擬，其模擬精度受閾值選取影響。有學者通過在燈光不敏感地區加入其他因素來提高模擬效果：文獻[18-19]在夜間燈光不敏感的農村貧困地區引入地區生產總值(gross regional product，GDP)和人口因素對NTL-EPC模型進行修正，修正后NTL與EPC表現出更好的相關性。

綜合前人研究發現，在一些農村貧困地區，引入其他因素對NTL-EPC模型進行修正是必須的，但也會增加計算復雜度。所以，適當選擇引入因素，是在復雜度和精度之間取得平衡的關鍵。這就需要對NTL影像在不同因素影響下作為EPC模擬指標的能力進行全面的檢驗，并確定其主要的影響因素。2016年，Xie等[20]基于1995—2001的DMSP-OLS衛星NTL影像建立了簡單的因素對數評估模型，評估了不同地區國家的人口城鎮化、富裕程度、技術水平、溫度和NTL分布模式對NTL-EPC關系的影響。結果表明，NTL與EPC之間存在較強的相關性，如果NTL保持穩定，國家EPC將隨人口城鎮化率、人均GDP和高科技出口的升高而增加。在東亞及太平洋地區，國家EPC將隨溫度的升高而減少，隨人類活動的集結而增加，且對各地區NTL-EPC關系造成關鍵影響的因素也不盡相同。在利用NTL對某些不太富裕的國家進行EPC模擬時，人均GDP和人口城鎮化率這些關鍵因素不可忽視。

而目前很少有研究在城市層面評估不同因素對NTL-EPC關系的貢獻度，并探討其主要的影響因素。IPAT方程是西方學者經過反復驗證的定量計算不同指標對環境影響的公式，常應用于CO2排放等領域，本文參照Xie等[20]的研究，將EPC也視為人類活動對環境的一種影響，根據IPAT公式將社會因素分為富裕指標、人口指標和技術指標，同時考慮燈光分布模式和城市年均溫度，探討以上各因素的加入對NTL-EPC關系的影響；同時，提出NTL-EPC模型可能的改進方向，以更加適合中國城市的電力消費模擬。

1 數據來源及處理

本研究使用的數據如表1所示，包含2013年DMSP-OLS衛星NTL影像、NPP-VIIRS衛星NTL影像、地級市人口城鎮化率、市轄區人口、年末總人口、人均GDP、地區GDP、第三產業占GDP的比重、科學技術支出、年均溫度以及城市邊界文件。

表1 數據來源及簡述

1.1 NPP-VIIRS數據的處理

NPP-VIIRS影像為每月發布，存在有噪聲、短時化學光源等問題，需要進行校正。參考文獻[21-22]的研究，NPP-VIIRS影像的校正主要解決以下2個問題：①影像中存在負值，且沒有關于負值像元的描述，假設像元的負DN值是由背景噪聲和數據處理的異常值引起，將其恢復為0；②影像中存在噪聲點或異常點。Shi等[6]提出，在中國國內，可以認為沒有比北京、上海和深圳三大城市最大亮度更高的亮度值。

結合前人方法，本文提出一種新的校正方案。使用2013年各月數據來計算年均數據。我們認為同一年中出現時間較多的、沒有異常突變升高或者降低的像素點為穩定的衛星NTL數據，值得保留。而那些出現次數很少或者亮度值突變的地方，可以認為是噪聲點或是由于火山、化學燃燒、天氣等原因產生的異常點，應該去除。利用這種理論，使用各月數據進行相互校正，過程如下。

1)計算北京、上海、深圳地區的最大亮度值DNmax，如果有DN>DNmax，將其置為DNmax。

2)將各月亮度值非負點設為1，負值和0點設為0，提出一個掩模，12個月掩膜相加得到全年掩模矩陣A，當A中的像素點值小于3時，認為它是異常點，將其歸零。

3)將各月圖像疊加，點除矩陣A，得到年均圖像。

(1)

1.2 研究區域

到2013年年底，中國內地共包含地級市290個。去除電力消費量未統計城市，本文研究城市共278個。參考李通等[15]的研究，為研究區域差異，如表2所示，將城市按省份經濟分區分為東部、中部、西部和東北地區，各包括84、81、84和29個地級市。對溫度因素進行研究時，將城市按是否集中供暖分為119個供暖城市和159個非供暖城市。

表2 按照經濟分區的城市劃分

2 模型構建

前人研究已經證明了衛星夜間燈光與電力消費量(NTL-EPC)之間的冪指數模型[23-25]，表達如式(2)所示。

EPC=a×NTLb

(2)

式中：EPC為城市的市轄區全社會用電量；NTL為城市的像元亮度DN值總和；b為系數；a為NTL之外的變量因素。IPAT方程是西方學者經過反復驗證的公式，如式(3)所示。

I=P×A×T

(3)

式中：I指環境影響；P、A和T分別代表對環境影響造成影響的人口指標、富裕指標和技術指標3種社會經濟因素[26]。

在馬忠玉等[1]的研究中，將人口密度和地區GDP加入NTL-EPC模型。在Xie等[17,20]的研究中，將人口城鎮化率作為人口指標，人均GDP作為富裕指標，高科技出口作為科技指標進行研究。本研究根據IPAT方程，將EPC視為人類活動對環境的一種影響，考慮前人研究中選取的社會經濟因素，以及《中國城市統計年鑒》中數據的完整性，選取人口城鎮化率和市轄區人口比例作為人口指標，地區GDP和人均GDP作為富裕指標，第三產業GDP占比和科學技術支出作為技術指標，研究以上指標對NTL-EPC關系的影響。前人研究指出，城市溫度和人類活動空間分布對電力消費量存在影響[27-28]。將年均溫度和燈光離散系數作為變量因素，研究其對NTL-EPC關系的影響。

將系數a分解[29]，其表達如式(4)所示。

a=k+SEα+eβ(CV)+eγ(AT)

(4)

式中：SE代表社會經濟因素；CV是燈光離散系數，用NTL的標準差除以平均值計算，CV越大，表示燈光分布越分散，往往也代表著人類活動越分散；AT表示年均溫度；k為常數；α、β、γ為系數。

為便于計算，將式(1)和式(3)變換為對數模型，如式(5)所示。

ln(EPC)=C0ln(NTL)+C1

C1=k+αln(SE)+β(CV)+γ(AT)

(5)

式中：C0為系數；C1為ln(NTL)之外的變量。其余參數含義與式(4)中一樣。

2.1 CV和AT對NTL-EPC關系的影響模型

僅考慮燈光離散系數CV對NTL-EPC關系的影響，其模型如式(6)所示。

ln(EPC)=kCV+C0ln(NTL)+βCV(CV)

(6)

式中：kCV為常數；C0、βCV為ln(NTL)和CV的系數。

僅考慮年均溫度對NTL-EPC關系的影響，其模型如式(7)所示。

ln(EPC)=kAT+C0ln(NTL)+γAT(AT)

(7)

式中：kAT為常數；C0、γAT為ln(NTL)和AT的系數。

2.2 不同社會經濟因素對NTL-EPC關系的影響模型

單一社會經濟因素對NTL-EPC關系的影響模型如式(8)所示。

ln(EPC)=k+βCV(CV)+γAT(AT)+

C0ln(NTL)+αln(SE)

(8)

式中：k為常數；βCV、γAT和C0分別為CV、AT和ln(NTL)的系數；SE代表社會經濟因素；α為ln(SE)的系數。

將式(8)中SE分別用人口指標P、富裕指標A和技術指標T替代，建立人口指標P對NTL-EPC關系的影響模型，如式(9)所示。

ln(EPC)=kP+βCV(CV)+γAT(AT)+

C0ln(NTL)+αPln(P)

(9)

式中：kP為常數；P為人口指標；αP為ln(P)系數。同理，富裕指標A對NTL-EPC關系的影響模型如式(10)所示。

ln(EPC)=kA+βCV(CV)+γAT(AT)+

C0ln(NTL)+αAln(A)

(10)

式中：kA為常數；A為富裕指標；αA為ln(A)系數。科技指標T對NTL-EPC關系的影響模型如式(11)所示。

ln(EPC)=kT+βCV(CV)+γAT(AT)+

C0ln(NTL)+αTln(T)

(11)

式中：kT為常數；T為科技指標；αT為ln(T)系數。

2.3 多因素影響下的NTL-EPC模擬模型

多因素影響下的NTL-EPC模擬模型如式(12)所示。

ln(EPC)=k+βCV(CV)+γAT(AT)+C0ln(NTL)+

αPln(P)+αAln(A)+αTln(T)

(12)

式中：k為常數；βCV、γAT和C0表示的含義與式(8)相同；P和αP含義與式(9)相同；A和αA含義與式(10)相同；T和αT含義與式(11)相同。

3 實驗與分析

學者們在研究NTL-EPC模擬模型時，通常將可決系數R2和模擬誤差作為模型的評估指標[1，5，15，20]。相比于模擬誤差，可決系數R2是一個無量綱系數，便于不同回歸模型之間的比較。R2有確定的取值范圍[0，1]，R2越接近1，說明回歸模型對觀測值的擬合程度越好。

本文參考文獻[15，20]的研究，選取R2作為評估指標，以此評估不同因素對NTL-EPC關系的貢獻度。另外參考經濟學中的討論方法，將通過顯著性檢驗的自變量系數視作偶然情況。

3.1 不同衛星的NTL-EPC相關關系

不添加任何影響因素的情況下，使用式(4)進行NTL-EPC對數模型模擬，結果如表3所示。表3中，未加粗數據為DMSP-OLS衛星模型回歸結果，加粗數據為NPP-VIIRS衛星模型回歸結果。a表示通過1%顯著性檢驗；b表示通過5%顯著性檢驗；c表示通過10%顯著性檢驗。全文所有表格皆采用此表示。DMSP-OLS衛星各地區模型中僅有中部模型R2(0.719)高于全國模型(0.477)，東北模型效果最差(R2=0.281)。NPP-VIIRS衛星地區模型中，東部和中部模型的R2都高于全國模型(0.768)，其中，中部模型R2最高，達到了0.833。

表3 不同衛星NTL-EPC對數模型

另外，NPP-VIIRS衛星全國和地區模型R2都高于DMSP-OLS衛星模型，相較于DMSP-OLS衛星，NPP-VIIRS衛星的NTL-EPC模型效果更好。

3.2 人口指標(P)對NTL-EPC關系的影響

人口城鎮化率表示城鎮人口占常住人口比例，國內數據在東北地區存在嚴重缺失。將其作為人口指標，根據式(9)進行模擬，結果如表4所示。除東北地區數據缺失外，相較于表3，2類衛星所有模型的R2都有提高。DMSP-OLS衛星擬合效果最好的是中部模型(R2=0.889)；NPP-VIIRS衛星中擬合效果最好的是東部模型(R2=0.904)。

另外，加入人口城鎮化率后，DMSP-OLS衛星全國和東部模型的R2都提高了1倍左右，分別為0.836和0.864，與NPP-VIIRS衛星模型效果相差甚小。中部和西部模型的R2甚至高于NPP-VIIRS衛星模型。

2類衛星的所有模型中，人口指標系數αP均為正數且通過顯著性檢驗，即NTL保持穩定時，城市EPC都隨人口城鎮化率的升高而增加。

人口城鎮化率數據在東北地區有所缺失，尋找更加全面的人口指標用以替代。在《中國城市統計年鑒》中發布了各地級市市轄區人口和全市人口數據，用市轄區人口除以全市人口獲得市轄區人口比例，將市轄區人口比例作為人口指標帶入模型，其模擬結果如表5所示。

表5中所有模型的R2都高于表4中人口城鎮化率作為人口指標時的模型，NPP-VIIRS衛星擬合效果最好的是東部模型(R2=0.922)；DMSP-OLS衛星擬合效果最好的是中部模型(R2=0.897)。與人口城鎮化率作為人口指標時一樣，加入市轄區人口比例后，DMSP-OLS衛星中部和西部模型R2比NPP-VIIRS衛星模型更高。

表4 人口城鎮化率對NTL-EPC關系的影響模型

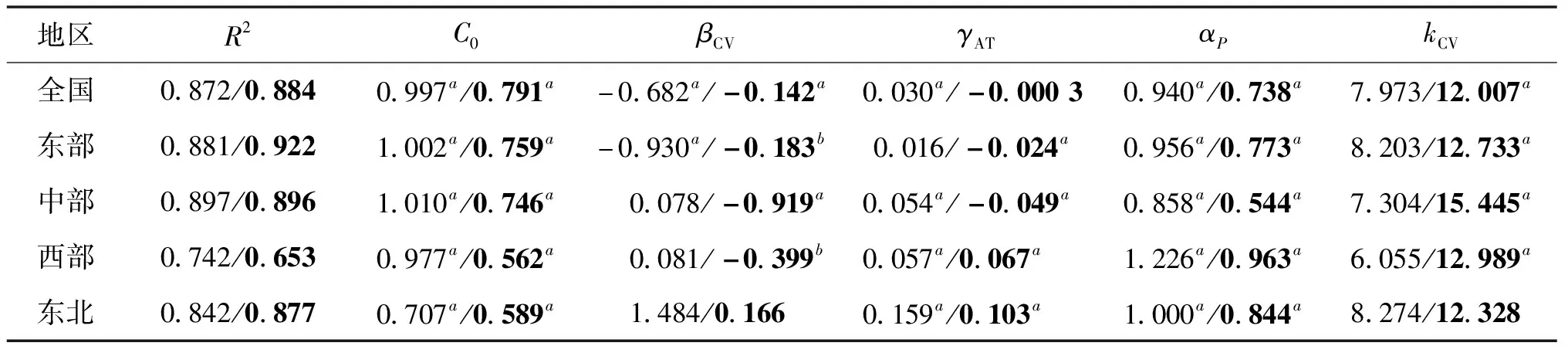
表5 市轄區人口比例對NTL-EPC關系的影響模型

在所有模型中，人口指標系數αP均為正數，即NTL保持穩定時，城市EPC都隨市轄區人口比例的升高而增加。

3.3 富裕指標(A)對NTL-EPC關系的影響

選取人均GDP作為富裕指標，根據式(10)進行模擬，結果如表6所示。相較于表2，2類衛星所有模型的R2都有提高。DMSP-OLS和NPP-VIIRS衛星擬合效果最好的都是中部模型，R2分別達到了0.831和0.849。加入人均GDP后，DMSP-OLS衛星的中部和西部模型R2與NPP-VIIRS衛星模型相差不大。2類衛星擬合效果最差的都是西部模型，R2均未達到0.6。

通過顯著性檢驗的富裕指標系數中，除西部模型外，所有模型的富裕指標系數αA均為正數，即NTL保持穩定時，城市EPC隨人均GDP的升高而增加。

由于人均GDP指標與人口指標有所關聯，另選地區GDP作為富裕指標進行模擬，以消除人均GDP作為富裕指標時引入的人口指標對模型的影響，結果如表7所示。從表7可見，所有模型的R2都高于表6中人均GDP作為富裕指標時的各模型。DMSP-OLS和NPP-VIIRS衛星擬合效果最好的都是東部模型，R2分別達到了0.927和0.933。加入地區GDP之后，DMSP-OLS衛星擬合效果提升明顯，全國和東北模型的R2更是高于NPP-VIIRS衛星模型，其他模型的R2也與NPP-VIIRS衛星模型相差不大。

表6 人均GDP對NTL-EPC關系的影響模型

表7 地區GDP對NTL-EPC關系的影響模型

所有模型的富裕指標系數αA均為正數且通過顯著性檢驗，即NTL保持穩定時，城市EPC隨地區GDP的升高而增加。

3.4 科技指標(T)對NTL-EPC關系的影響

選取第三產業GDP占比作為科技指標，根據式(11)進行模擬，結果如表8所示。相較于表2，2類衛星所有模型R2都有提高。DMSP-OLS衛星擬合效果最好的是東部模型(R2=0.758)，NPP-VIIRS衛星擬合效果最好的是東北模型(R2=0.850)。加入第三產業GDP占比之后，DMSP-OLS衛星全國和東部模型R2提高1倍左右，東北模型R2提高2以上，中部模型R2與NPP-VIIRS衛星模型相差甚小。

2類衛星東部和中部模型中的科技指標系數αT均為正數且通過顯著性檢驗，即NTL保持穩定時，東部和中部城市EPC隨第三產業GDP占比的升高而增加。而在東北地區，科技指標系數αT未通過顯著性檢驗。2類衛星全國和西部模型中αT的符號不一致。

第三產業GDP占比會受到第三產業GDP、第二產業GDP和地區GDP的影響，而第二產業也是影響EPC的一大因素。另外選取科學技術支出作為科技指標，以消除第三產業GDP比例作為科技指標時引入的富裕指標對模型的影響，結果如表9所示。從表9可見，所有模型的R2都高于表8中第三產業GDP占比作為科技指標時的各模型。DMSP-OLS衛星擬合效果最好的是中部模型(R2=0.897)；NPP-VIIRS衛星擬合效果最好的是東部模型(R2=0.895)。加入科學技術支出后，DMSP-OLS衛星模型R2提高明顯，全國和東部模型R2與NPP-VIIRS衛星模型相差不大。中部和西部模型R2甚至超過了NPP-VIIRS衛星模型。

表8 第三產業GDP占比對NTL-EPC關系的影響模型

表9 科學技術支出對NTL-EPC關系的影響模型

所有模型的科技指標系數αT均為正數，即NTL保持穩定時，城市EPC隨科學技術支出的升高而增加。

3.5 多因素影響下的NTL-EPC模型

考慮指標的完整性和表2～表9中不同指標對NTL-EPC關系的影響，選取市轄區人口比例作為人口指標，地區GDP作為富裕指標，科學技術支出作為科技指標，根據式(12)建立多因素影響模型。模型回歸結果如表10所示。

表10 多因素影響下的的NTL-EPC模型

DMSP-OLS和NPP-VIIRS衛星模型的擬合效果相差不大。單獨考慮人口指標、富裕指標和科技指標，通過顯著性檢驗的系數中，除東部地區的科技指標系數外，都為正數，與前文描述相符，即當NTL不變時，城市EPC隨社會經濟的發展而增加。

對于東部模型，富裕指標系數最大，即地區GDP的增加對城市EPC的促進作用大于市轄區人口比例的上升，而城市科學技術支出的增加對EPC有抑制作用。中部地區，市轄區人口比例上升對城市EPC的促進作用更加明顯。西部地區，地區GDP增加對城市EPC的促進作用大于市轄區人口比例上升和科學技術支出增加。東北地區，地區GDP增加對EPC的促進作用大于市轄區人口比例增加，而科學技術支出系數沒有通過顯著性檢驗，不具有代表性意義。

3.6 離散燈光系數(CV)和溫度(AT)對EPC影響

表4至表10的NPP-VIIRS衛星和DMSP-OLS衛星模型中，所有通過顯著性檢驗的βCV均為負，即NTL保持穩定時，EPC隨人類活動的聚集而增加，而溫度系數γAT隨地區和社會經濟因素的變化而變化。可能不同因素的加入導致的樣本變化會影響2個系數。

僅考慮CV對NTL-EPC關系的影響，根據式(6)進行模擬，結果如表11所示。表中所有模型CV系數βCV均為負值，即NTL保持穩定時，EPC隨人類活動的聚集而增加。

表11 燈光離散系數對NTL-EPC關系的影響模型

僅考慮溫度對NTL-EPC關系EPC的影響，根據式(7)進行模擬，結果如表12所示。所有模型溫度系數γT均為正值，即NTL保持穩定時，EPC隨溫度的升高而增加。

表12 溫度對NTL-EPC關系的影響模型

研究供暖城市和非供暖城市溫度對NTL-EPC關系的影響，結果如表13所示。在供暖和非供暖區域，NTL保持穩定時，城市EPC隨年均氣溫的升高而增加。

表13 溫度對供暖城市和非供暖城市NTL-EPC關系的影響模型

4 討論

4.1 不同衛星的NTL-EPC相關關系

不添加任何因素情況下，NPP-VIIRS衛星模型擬合效果優于DMSP-OLS衛星(表3)。2016年，江威等[30]對比了2種夜間燈模擬社會經濟參量的潛力，也提出NPP-VIIRS衛星在對全社會用電總量的模擬中占有優勢。前人研究中提到，DMSP-OLS衛星NTL影像有以下2個缺點[3，15-17]。

1)在城市中心區域存在像元飽和現象，這可能是造成表3中東部地區擬合效果不理想的原因。

2)貧困、人口稀少地區的大量EPC未被NTL影像捕捉，這可能是表3中西部地區擬合效果不理想的原因。對于東北地區而言，工業產生的EPC是東北地區EPC不可忽視的組成部分，而這部分的EPC并未表現在夜間燈光影像上，這可能是造成表3中東北地區擬合效果不理想的原因。

相較于DMSP-OLS衛星影像，NPP-VIIRS衛星影像不存在城市中心像元飽和問題，所以其模型擬合結果優于DMSP-OLS衛星。但NPP-VIIRS衛星影像依然未捕捉到西部貧困地區的大量EPC和東北地區工業產生的EPC，所以表3中NPP-VIIRS衛星的西部和東北模型R2依然低于全國水平。

加入一些社會經濟因素指標后，DMSP-OLS的某些地區模型擬合效果反而高于NPP-VIIRS衛星模型，但相差不大。

4.2 社會經濟因素不可忽視

如表4至表9所示，加入不同社會經濟因素之后，會提高NTL-EPC模型的擬合效果。特別是西部貧困地區和東北地區，大量EPC未被燈光捕捉，加入社會經濟因素會對模型效果有明顯提升。

在利用DMSP-OLS衛星的NTL對EPC進行城市模擬時，貧困地區的社會經濟因素不可被忽略。文獻[18-19]在國家層面和地區層面的研究也證明了這一結論。同樣，工業為主的地區的社會經濟因素也不可忽略。

4.3 燈光離散系數(CV)、年均溫度(AT)和社會經濟因素對EPC的影響

1)燈光離散系數(CV)對EPC的影響。CV指燈光的離散程度，在一定程度上也可以反映人類活動的聚集程度。CV越大，燈光越分散，人類活動越分散。Xie等[20]的研究中指出，在東亞及太平洋地區，人類活動越聚集(CV小)的國家EPC越小。在本研究中也有城市EPC隨人類活動的聚集而增加的情況，與Xie等對國家層面的研究結果保持一致。

2)溫度對EPC的影響。溫度的加入對NTL-EPC模型的模擬結果有一定的提升。這是由于溫度變化，空調制冷、取暖產生的EPC并未被衛星NTL影像所記錄。

Xie等[20]的研究中指出，國家EPC隨溫度的升高而減少。而本研究結果與其不同，城市EPC隨溫度的升高而增加。這是因為Xie等的研究在東亞即太平洋地區，年均溫度更高，更靠近赤道的國家，大部分為東南亞發展中國家，這類國家的EPC更低，更大的原因是因為其國家發展程度不高，而Xie等在研究中并沒有剔除國家的社會經濟因素對EPC的影響。

由于我國冬季有部分地區集中供暖的特殊國情，在研究溫度對EPC的影響時，供暖與非供暖城市的EPC并不能單純進行比較。集中供暖地區冬季供暖以燒煤為主，不用耗費大量電力，其EPC受溫度影響主要體現在夏季制冷，所以EPC隨溫度的升高而增加。而非供暖城市EPC受溫度影響在夏季制冷和冬季取暖都有體現，但冬季取暖也有燒煤等方法，還是夏季制冷的影響更加明顯，所有EPC也隨溫度的升高而增加。

3)社會經濟因素對EPC的影響。表4至表9中，各社會經濟因素的加入對模型的擬合效果均有提升。因為隨著城市人口、富裕程度和科技水平的發展，城市交通發展，服務業發展和電子產品使用等產生的EPC未被衛星NTL影像記錄。

人口城鎮化率數據在東北地區嚴重缺失。人均GDP將人口數據作為分母進行模擬時會引入人口指標對EPC的影響。第三產業GDP占比作為科技指標進行模擬時會引入富裕指標和工業對EPC的影響。考慮全面數據對模擬結果的提升和獨立性，市轄區人口比例、地區GDP和科學技術支出是更加理想的人口指標、富裕指標和科技指標。

Xie等[20]研究中指出，NTL保持穩定時，國家EPC隨人口城鎮化率、人均GDP和高科技出口的升高而增加。本文得出結論為：NTL保持穩定時，城市EPC隨市轄區人口比例、地區GDP和科學技術支出的升高而增加，除東北地區數據不完整外，城市EPC也隨人口城鎮化率的升高而增加，這一結果與Xie等對國家層面的研究保持一致。除西部地區外，城市EPC隨人均GDP的升高而增加。Xie等研究中南非這類貧困地區，城市的EPC隨人均GDP的升高而減小，與我國西部地區模型表現一致。在西部和東北地區，城市的EPC隨第三產業占比的升高而減小，東北地區以工業為主，第三產業的升高反而造成第二產業的降低，減小了工業產生的EPC。

4)不同社會經濟因素對EPC的影響程度。從表10可以看出，對于東部地區，地區GDP的增加對城市EPC的促進作用大于市轄區人口比例的上升，而城市科學技術支出的增加對EPC有抑制作用。可以解釋為東部地區城市幾乎是發達城市，城市人口急劇增加帶來城市發展的階段已經基本過去，所以人口的增加不會太大程度影響城市的發展，進而影響城市EPC。而對于發達城市，更多科學技術支出的城市有更雄厚的資金來研發新型能源，從而減小城市EPC。

對于中部地區，市轄區人口比例上升對城市EPC的促進作用更加明顯。中部城市處于發展中階段，這一階段城市的發展必然會伴隨著市轄區人口比例的上升，地區GDP和科學技術支出的增加，而城市EPC也會增加。

對于西部貧困地區，地區發展以GDP的增加為首要任務，地區GDP增加對城市EPC的促進作用大于市轄區人口比例上升和科學技術支出增加。

對于全國模型，當NTL一定時，地區GDP的增加對城市EPC的促進作用大于市轄區人口比例的增加；而科學技術支出對于城市EPC的影響不具有代表性意義。

對比幾類模型可以得出，城市的發展可以分為以下幾個階段：第一階段，城市屬于貧困城市，城市的發展以發展經濟為主，此時城市對于人才的吸引力并不大，所以城市EPC增加的主要影響因素為富裕因素；第二階段，城市發展經濟到一定階段，對于人才具備一定吸引力，此時有大量人口涌入城市，人口指標成為影響城市EPC的最主要因素；第三階段，城市發展到一定規模，人口基本飽和，此時影響城市EPC的主要因素又回歸到地區GDP，而在此階段，城市有能力投入更多資金進行研發以減少城市的EPC、CO2排放等。在城市發展過程中，科技指標對城市EPC排放的作用是先促進，后抑制。

4.4 模型改進方向

可以發現，對于NTL-EPC的模擬，在加入不同因素后都會有所提升，但還是存在誤差。其原因可能有以下幾個方面。

1)數據本身存在缺陷。燈光數據無法探測到一些室內耗電如空調、電子產品等，且衛星影像對貧困地區的大量EPC未能捕捉。

2)模型本身過于簡化。不同的社會經濟因素、溫度和燈光分布等都能捕捉到部分燈光未捕捉的EPC。所以，僅將NTL作為EPC模擬的唯一數據源是不夠的。

3)分類方式不合理。城市發展模式多種多樣，按經濟分區只是其中一種，還有南北劃分、城市等級劃分等更加多樣的劃分方法。例如單對于溫度因素來說，供暖和非供暖城市的劃分方法顯然比經濟分區劃分更加具有解釋性。

另外，本研究建議在進行NTL-EPC模擬時，應考慮富裕程度、城市化、技術水平、溫度和NTL分布等因素作為輔助變量。但模型也不適宜太過復雜，因為作為城市的估算模型，需要考慮到城市本身的樣本基數不同于省域，太過復雜的樣本會大大增加其計算復雜性。

最后，在統計數據中還有很多指標與電力消費有關，例如城市綠地面積、工業產值等，在模型復雜度允許的情況下，可以盡量多地加入一些其他指標來提高模型精度。

5 結束語

本研究基于前人提出的NTL-EPC對數模型，加入人口城鎮化率、市轄區人口比例、地區GDP、人均GDP、第三產業占GDP的比重、科學技術支出，年均溫度和燈光分散系數等指標。考察富裕程度、人口、技術水平、溫度和燈光分布對NTL-EPC關系的影響，探討了影響NTL-EPPC關系的關鍵因素。

結果表示，相較于DMSP-OLS衛星，NPP-VIIRS衛星的NTL與EPC具有更好的相關性。當城市NTL保持穩定時，城市EPC隨人類活動的聚集和溫度的升高而增加；隨市轄區人口比例、地區GDP，科學技術支出的升高而增加；除西部和東北地區，城市EPC隨人均GDP和第三產業GDP占比的升高和而增加。

針對城市層面的電力消費模擬，在以后的研究中，可以適當加入社會經濟因素，尋找更為合理的城市分類方法來優化NTL-EPC模型。另外，還可以建立更為復雜的多因素影響模型，但要考慮優化效果和復雜度之間的取舍。