一種快速有效的正弦波信號頻率估計方法?

溫兵會 毛衛寧

(1 東南大學網絡空間安全學院 南京 210096)

(2 東南大學信息科學與工程學院 南京 210096)

0 引言

正弦波信號的頻率估計是數字信號處理領域的一個值得研究的經典課題，在聲吶、雷達等領域應用廣泛。采用離散傅里葉變換(Discrete Fourier transform,DFT)譜估計方法估計正弦波信號的頻率是一種常用方法，由于快速傅里葉變換(Fast Fourier transform,FFT)算法的高效性，該方法在工程上得到廣泛應用[1?3]。利用FFT 譜估計法進行正弦波信號頻率估計的方法很多，大體上可以分為兩類。一類是需要判別頻率修正方向的算法，如Rife算法[4?5]、M-Rife算法[6]和I-Rife算法[7]。Rife算法是正弦信號頻域頻率估計的經典算法，通過頻譜插值對實際頻率相對于譜線最大值頻率的偏移量進行估計，計算量小，但是存在兩個問題：一是當實際頻率在譜線最大值頻率附近時，頻率估計誤差相對較大；二是，其頻率估計精度易受噪聲的影響，低信噪比(Signal-to-noise ratio,SNR)時估計性能下降。M-Rife算法解決了Rife算法的第一個問題，但增加了運算量。I-Rife算法解決了Rife算法的兩個問題，但進一步增加了計算量。Rife算法、M-Rife算法和I-Rife算法存在的共同問題是需要判別頻率修正方向，再計算頻率偏差。另一類，基于FFT的頻率估計方法，不需要判別頻率修正方向，直接計算頻率偏差，如Candan算法[8]、Fang算法[9]和改進的Fang算法[10?12]。Candan算法計算簡單，但當信噪比較低時，容易出現插值方向錯誤，導致誤差較大。Fang算法通過對信號在時域補等信號長度的零，采用FFT頻譜中最大譜線相鄰的兩根譜線幅度估計頻率偏差，提高了頻率估計性能，但增加了計算量。改進的Fang算法在Fang算法基礎上提高了頻率估計性能，減少了計算量。Candan算法和Fang算法及其改進算法存在的共同問題是涉及到非線性函數的計算，增加了算法的復雜度。為此，本文提出了一種新的頻率估計算法，在N點FFT運算基礎上，利用兩點細化的頻譜值估計頻率偏移量，分析了頻偏估計的偏差和算法的復雜度。相比于I-Rife和改進的Fang算法，本文不需要判別頻率修正方向，降低了算法計算量和復雜度。

1 問題描述

含有噪聲的復正弦信號為

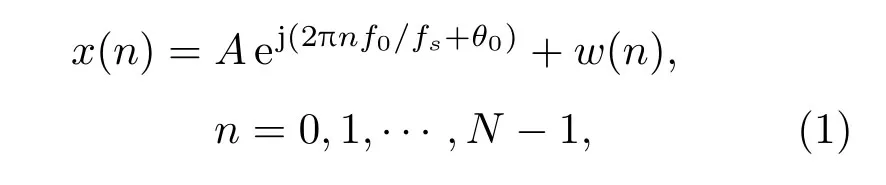
其中，f0=(k0+δ)·?f為信號頻率，?f=fs/N為頻率分辨率，δ為數字頻率偏差，取值范圍在?0.5～0.5之間，fs為采樣頻率，k0為數字頻率；w(n)為高斯白噪聲，均值為0，方差為A和θ0分別為信號幅度和初相；N為信號長度。

對式(1)所示的信號進行N點DFT得到

式(2)中，W(k)表示高斯白噪聲的DFT，在不考慮噪聲的情況下信號傅里葉變換的幅值為

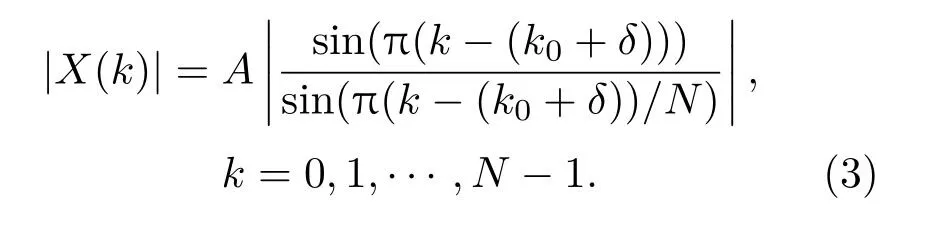
當信號的真實頻率不等于頻率分辨率?f的整數倍時，利用FFT 估計頻率存在頻率偏差，數字頻率偏差δ取值范圍在?0.5～0.5之間，信號的真實頻率位于譜線最大值與次大值對應的頻率之間。

假設信號經過N點FFT 運算后，頻譜幅度最大值為|Xk0|，對應的數字頻率為k0，次大值為|Xk0+α|。Rife算法利用頻譜幅度的最大值和次大值估計頻率偏差，頻率估計公式為[4]

其中，頻率修正方向α=±1。當|Xk0+1| >|Xk0?1|時，α=+1；當|Xk0+1|<|Xk0?1|時，α=?1。

Rife算法計算量小，但在頻偏較小時，頻率估計誤差增大，此外，低信噪比時估計性能下降；I-Rife算法[7]是對Rife算法的改進，利用頻譜細化技術計算譜值|X(k0±0.5)|作為頻率修正方向的判據，利用頻移技術將被估計頻率移至兩相鄰數字頻率的中心處，以確保Rife算法能夠準確估計頻率。I-Rife算法在一定程度上克服了Rife算法的不足，但增加了計算量；改進Fang算法(I-Fang)[10]利用DFT計算6個頻點的譜值來估計數字頻率偏差，避免了Fang算法中對信號補等長度的零進行2N點FFT運算，減少了計算量，但利用I-Fang算法進行頻率估計同樣涉及到非線性函數的計算，算法復雜度較高。I-Fang算法性能與I-Rife算法接近，但計算量進一步增大，兩者在很低信噪比時，依然存在性能下降和不穩定問題。

2 本文算法和偏差分析

2.1 本文算法

為了提高低信噪比時的頻率估計性能，同時減小計算量，本文提出一種快速有效的頻率估計方法，運用頻譜細化方法計算頻譜值|X(k0±0.5)|，利用這兩點譜值估計數字頻偏，不需要判別頻率修正方向，提高了頻率估計的穩定性。

根據式(3)，k0點左右相鄰兩點頻譜幅度的比值為

式(5)中由于(π(k?δ)+π(k+δ))/2 =kπ，則|sin(π(k?δ))|=|sin(π(k+δ))|，假設π(k?δ)?N和π(k+δ)?N，則由公式(5)可得數字頻率偏差估計值：

當k=1時，即利用FFT 頻譜中的|X(k0?1)|和|X(k0+1)|值來估計數字頻偏δ，對應的表達式如下：

式(7)利用頻譜值|X(k0?1)|和|X(k0+1)|計算數字頻偏易受噪聲的影響，為了提高低信噪比下的頻率估計精度，利用頻譜細化獲得頻譜值|X(k0?0.5)|和|X(k0+0.5)|，代入式(6)得到

信號頻率的估計值為

本文提出的頻率估計算法的流程如下：

步驟1 對采樣信號進行N點FFT 運算，尋找幅度譜最大值對應的數字頻率k0。

步驟2 利用頻譜細化方法計算|X(k0±0.5)|兩點譜值。

步驟3 利用式(8)和式(9)估計信號頻率。

2.2 偏差分析

本文算法得到的數字頻率偏差表示式簡單，計算量小，進一步分析表明，還可以得到無噪聲情況下頻偏的偏差閉合表示式，可用于頻率偏差校正，以進一步提高測頻精度。

數字頻偏δ估計的偏差定義為

根據式(9)和式(10)，頻率估計的偏差為

因為數字頻率偏差的偏差bδ與頻率偏差bf之間的關系是線性的，因此只需分析數字頻偏的偏差bδ。

sin(π(0.5+δ)/N)和sin(π(0.5?δ)/N)是關于δ的函數，對其進行泰勒級數展開，在無噪聲情況下，根據式(8)和式(10)可得

有噪聲時，定義與信噪比有關的數字頻偏的偏差為

可以證明，至少存在一個SNR值γ滿足bδ(γ)=0。證明過程如下：

根據式(8)和式(13)可得

其中，

根據公式(2)可得

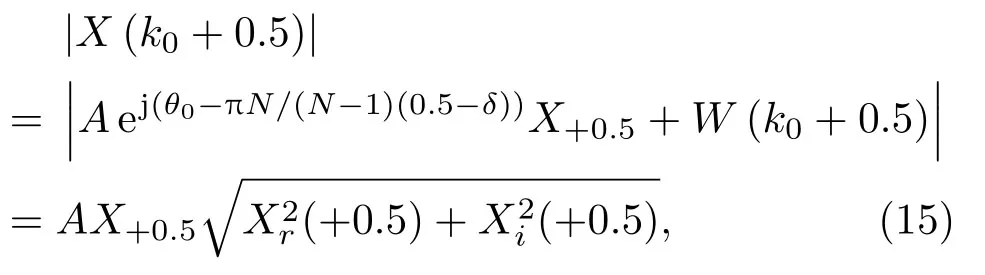
其中，X+0.5=sin(π(0.5?δ))/sin(π(0.5?δ)/N)，W(k0+0.5)表示復高斯噪聲。

Wr(k0+0.5)～N(0,1)和Wi(k0+0.5)～N(0,1)，因此，可以得到包含高斯隨機變量的|X(k0+0.5)|的形式為

其中，K=cos(θ0?π(N?1)/N(0.5?δ))Wr(k0+0.5)+sin(θ0?π(N?1)/N(0.5?δ))Wi(k0+0.5)。

當SNR滿足γ →0時，根據式(16)可得

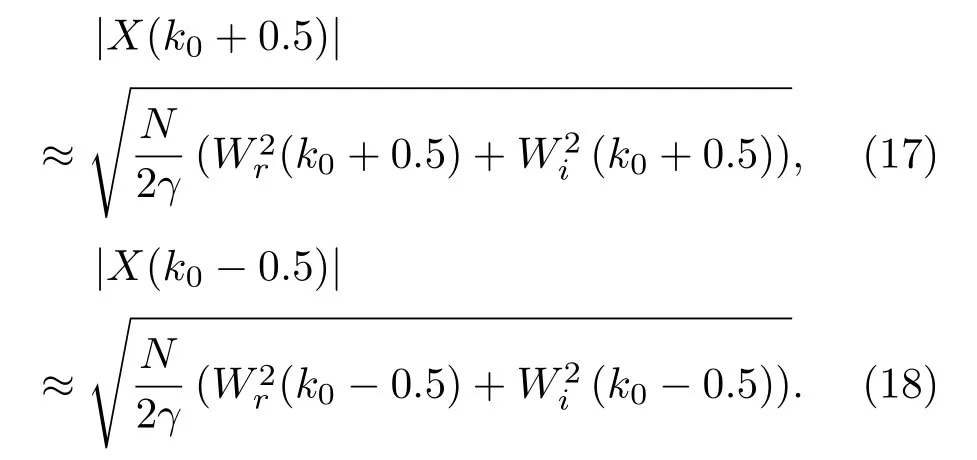
可以證明W(k0+0.5)和W(k0?0.5)是不相關的。Wr(k0+0.5)、Wi(k0+0.5)、Wr(k0?0.5)和Wi(k0?0.5)不相關，且具有相同的分布，則根據式(17)和式(18)可得

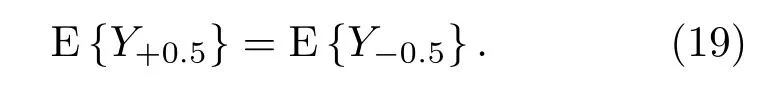
另一方面，當SNR取值滿足γ →+∞時，它將近似于無噪聲的情況，根據公式(12)，偏差bδ(+∞)和δ有相同的符號。

其中，sgn(·)表示符號函數。如上所述，高SNR和低SNR情況下，偏差的正負號是相反的。因此，存在至少一個SNR值γ0滿足bδ(γ0)=0。

3 計算量與性能分析

3.1 仿真實驗及性能分析

信噪比定義為SNR =采樣頻率fs=48 kHz，信號長度N=4800，頻率分辨率?f=fs/N=10?f=fs/N=10 Hz，信號頻率為f0=(256+0.10)?f/2。對于復正弦信號，在頻率、幅度、相位參數均未知的情況下頻率估計的克拉美羅界(Cramer-Rao lower bound,CRLB)[9]為

為了驗證本文算法的頻率估計性能，把本文算法與Rife算法[5]、I-Rife算法[7]、Candan算法[8]和I-Fang算法[10]進行頻率估計性能比較。1000次Monte Carlo仿真，信噪比變化范圍為?22～20 dB，數字頻偏δ=0.1，本文算法及以上幾種算法的頻率估計均方根誤差和頻率估計偏差隨信噪比的變化如圖1和圖2所示。

圖1和圖2表明，當信噪比大于10 dB時，5種算法頻率估計性能接近；信噪比小于10 dB時，Rife算法的頻率估計性能最差，Candan算法性能次之，I-Rife算法、I-Fang算法和本文算法估計性能接近。

圖1 頻率估計均方根誤差隨信噪比變化Fig.1 Frequency estimation root mean square error varies with SNR

圖2 頻率估計偏差隨信噪比變化Fig.2 Frequency estimation bias varies with SNR

取信噪比SNR =?22 dB，數字頻率偏差變化范圍為?0.5～0.5，比較5種算法頻率估計的均方根誤差隨數字頻偏的變化，結果如圖3所示。本文算法頻率估計均方根誤差基本上不隨頻偏變化，較Rife算法有很大的改善，性能與I-Rife算法和I-Fang算法相當。

圖3 頻率估計均方根誤差隨數字頻偏δ 變化(SNR=?22 dB)Fig.3 Frequency estimation root mean square error varies with digital frequency offset(SNR =?22 dB)

3.2 計算量分析

I-Rife算法除需要一次N點FFT 運算外，還要利用DFT計算4個頻點的譜值。I-Rife算法共需要進行(N/2·log2N+ 4N)次復數乘法和(N·log2N+4(N?1))次復數加法。Fang算法共需要進行N·log2(2N)次復數乘法和2N·log2(2N)次復數加法。本文算法要計算一次N點FFT和2個頻點的譜值，共需要進行(N/2·log2N+2N)次復數乘法和(N·log2N+2(N?1))次復數加法。改進的Fang算法[10]要計算一次N點FFT和6個頻點的譜值，共需要進行(N/2·log2N+6N)次復數乘法和(N·log2N+6(N?1))次復數加法。當N取不同值時，4種算法計算量如圖4所示。

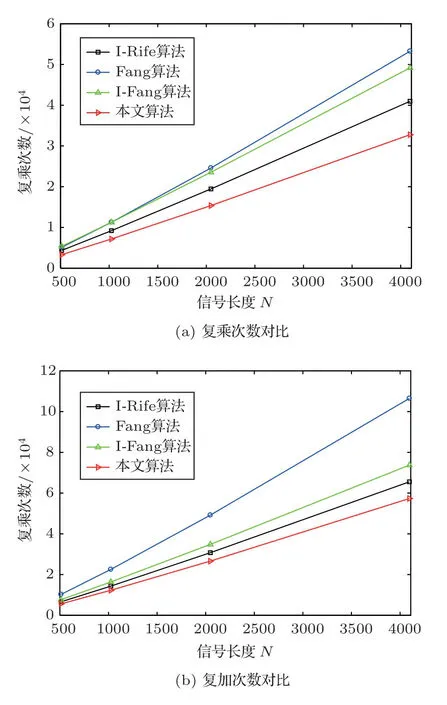
圖4 4種算法計算量隨信號長度變化Fig.4 The calculation amount of the four algorithms varies with the signal length

圖4表明，Fang算法的計算量最大，I-Fang算法的計算量次之，I-Rife算法的計算量再次之，本文算法的計算量最小。隨著N取值的不斷增大，本文算法的計算量相比I-Rife算法和I-Fang算法更小，更有優勢。

4 結論

本文提出了一種利用一次N點FFT和兩點細化的頻譜值|X(k0±0.5)|精確估計正弦信號頻率的方法，分析了頻偏估計的偏差和算法計算量。相比于I-Rife和I-Fang算法，本文算法不需要判別頻率修正方向，算法復雜度低，計算量小，在保證性能的同時，提高了算法的穩定性和實用性。綜上，本文算法的整體性能優于I-Rife算法和I-Fang算法，是一種快速有效的頻率估計方法。