基于模糊信息粒化和優化支持向量機的氧化鋁陶瓷超聲磨削力趨勢預測

趙明利 袁一鳴 李博涵 聶立新

（河南理工大學機械與動力工程學院，焦作 454000）

文 摘 為實現超聲磨削氧化鋁陶瓷中磨削力變化趨勢的預測，提出了一種基于模糊信息粒化和支持向量機相結合的方法。首先進行氧化鋁陶瓷超聲磨削試驗，然后利用模糊信息粒化方法對試驗獲得的磨削力進行粒化處理，并將人工免疫系統算法和粒子群算法進行并聯混編構成人工免疫系統粒子群算法（AISPSO），接著建立非線性回歸支持向量機預測模型并對模糊粒子進行預測，并通過AISPSO 算法優化支持向量機預測模型，最后獲得超聲磨削氧化鋁陶瓷中磨削力的變化趨勢和變化范圍。結果表明：該方法可以有效實現超聲磨削中磨削力的變化趨勢及變化范圍預測，且預測未來5 組數據變化范圍的誤差在10%以內，這為通過磨削力變化調整工藝參數以獲得更好的加工表面提供了新的思路。

0 引言

陶瓷材料因其抗腐蝕、耐高溫、耐磨損等優異性能，目前已廣泛應用于汽車行業、機械行業以及航空航天等領域［1］。隨著陶瓷材料的廣泛應用，對其表面質量提出了更高的要求。由于超聲磨削可以有效降低陶瓷加工中的磨削力［2］。同時磨削力也是表征磨削狀態的重要加工參數，是影響被加工零件精度和表面質量的關鍵因素，所以通過對磨削力變化趨勢進行預測，可以即時反饋調節加工參數，進而降低磨削力［3］，獲得更好的表面質量。

目前切削力預測方面常用的預測方法包括有限元仿真［4-5］、BP神經網絡［6-7］、支持向量機［8-9］等。如黃智［4］等基于磨削單位面積有效磨粒的砂帶磨削力計算模型，通過有限元仿真模型實現對磨削力的預測；秦娜等［6］通過遺傳算法優化BP神經網絡建立磨削力預測模型，利用工藝參數對磨削力進行預測；張海鷹等［8］利用最小二乘支持向量機建立振動切削力軟測量模型，并驗證了該模型具有較高的建模精度和較強的泛化能力。但是這些預測方法大多采用經驗公式建立仿真模型，或根據工藝參數來預測磨削力，然而實際磨削過程存在多種不確定因素，難以實現精確預測，而磨削力的變化趨勢和范圍的預測方法鮮有報道。本文提出一種基于模糊信息粒化（Fuzzy information granulation，FIG）和支持向量機（Support vector machines，SVM）在氧化鋁陶瓷超聲磨削中的磨削力變化趨勢預測算法。

1 超聲磨削的磨削力變化趨勢預測原理

1.1 模糊信息粒化

模糊信息粒化就是用模糊集的方法對時間序列進行模糊粒化處理，最早由L.A.Zadeh 教授［10］提出，其中信息粒化就是將整體分解為一個個部分進行研究，每個部分為一個信息粒。采用W.Pedrycz的粒化方法［11］，其模糊粒子有高斯型、梯型、三角形和拋物型等。本文采用三角形模糊粒子，其隸屬函數如下：

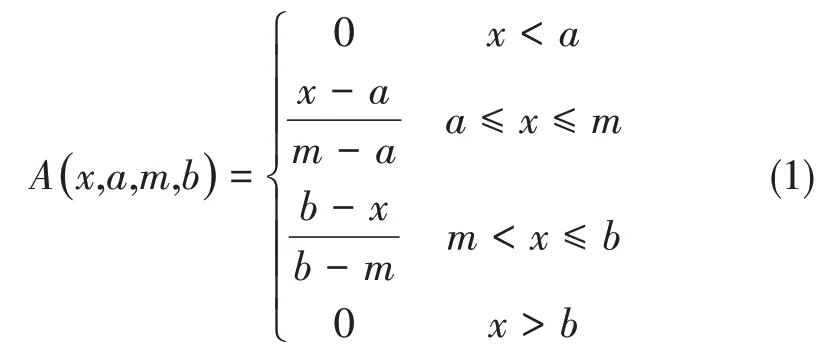
式中，x是論域中的變量，a、m、b為三角形模糊粒子的參數，a表示一個模糊窗口的最小值，m反映平均水平，b代表最大值。

1.2 非線性回歸支持向量機預測模型

支持向量機［12］是一種基于統計學習理論的機器學習方法，具有完備的數學基礎，且能夠很好地應用于小樣本、非線性、高維度等問題。其回歸預測模型的基本原理就是利用非線性變換（核函數）將低維空間映射至高維空間，并在該高維空間中找到一種輸入、輸出間的線性關系［13］。

在支持向量機回歸問題中，對于給定訓練集樣本D=｛（xi，yi）｝，i=1，2，3，…，l，其中xi∈Rn，yi∈R。可得到非線性回歸函數：

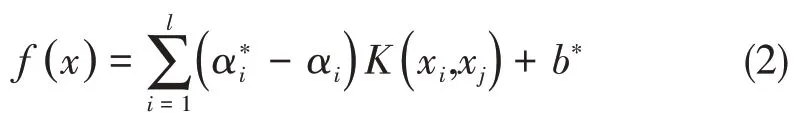
式中，αi表示第i個x的系數，αi*表示最優解，b*表示偏置函數，K（xi，xj）表示核函數。

在支持向量機應用過程中，核函數及其參數選擇至關重要。常用的核函數有多項式核函數、線性核函數、RBF 核函數和Sigmoid 核函數等。本文選取泛化性較強的RBF核函數，其公式如下：

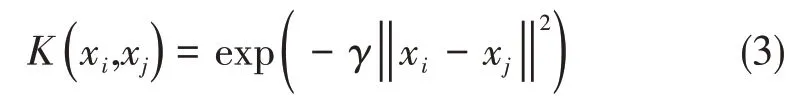
式中，γ為核參數，且γ＞0。

在非線性回歸支持向量機預測模型中，懲罰參數C和核參數γ對預測效果影響較大，且沒有固定的參數選擇方法。因此，本文通過智能優化算法對懲罰參數C和核參數γ進行選擇。

1.3 人工免疫系統粒子群優化算法

人工免疫系統粒子群算法（Artificial immune system particle swarm optimization，AISPSO）由粒子群算法（Particle swarm optimization，PSO）和人工免疫系統（Artificial immune system，AIS）進行并聯混編構成。通過親和力評價算子、抗體濃度算子、激勵度算子對粒子質量進行評價，并通過免疫選擇算子、克隆增殖算子、變異算子對質量相對較差的粒子進行變異，保持種群粒子的速度，以保證粒子的多樣性，改善了PSO算法易陷入局部收斂的情況，使之具有高效的尋優能力。

在AIS算法中，免疫選擇策略是使高激勵度粒子進入免疫操作、低激勵度粒子消亡并初始化更新，其目的為保持并提高AIS 算法中的粒子質量。本文提出一種與之相反的選擇策略，該策略使激勵度相對較低的小部分粒子進入免疫操作，激勵度相對較高的大部分粒子進入粒子群操作，并對閾值進行了改進，保證質量相對較好的粒子進入粒子群操作，質量相對較差的粒子進入免疫操作進行變異，保持種群的多樣性，使種群陷入局部收斂后具有快速跳出的能力，其公式如下：

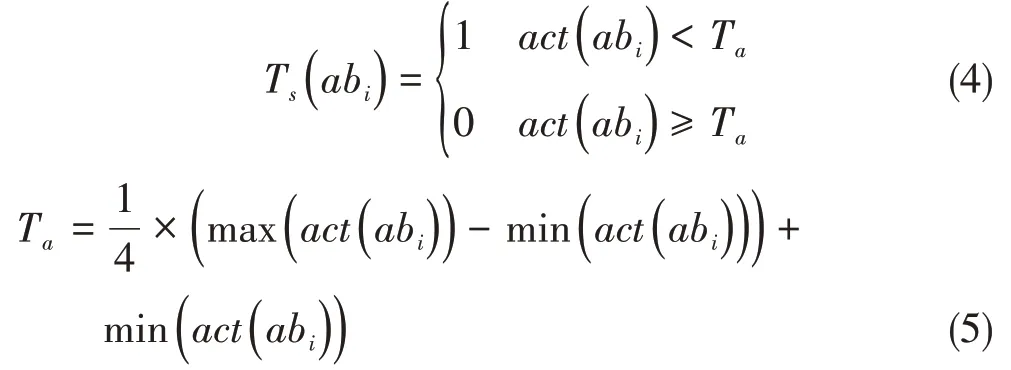
式中，Ta為閾值，abi表示粒子位置，act表示激勵度。

為改善AIS 算法的變異策略有一定概率覆蓋不到理論最優位置的問題，本文將最優位置轉移至邊界公式上［14］，并采用Tent混沌映射函數代替rand函數，采用的變異方案如下：

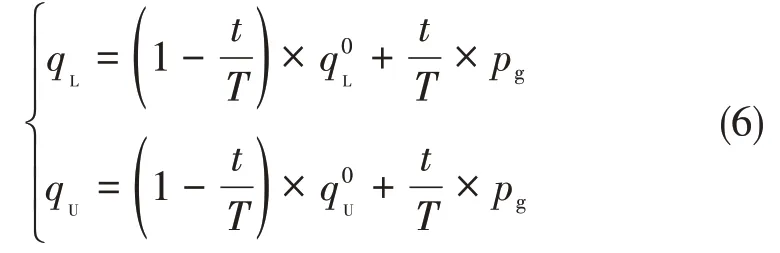
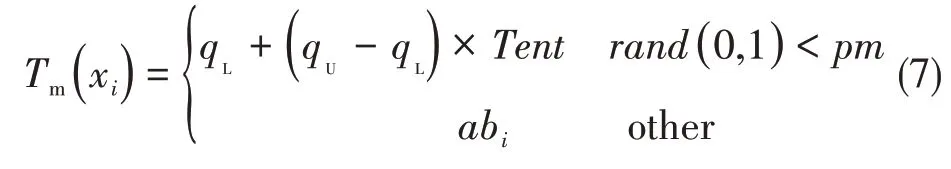
式（6）中，qL為當前搜索空間下限、qU為當前搜索空間上限，T為最大迭代次數，pg為當前全局最優。式（7）中，pm為變異閾值。

1.4 預測模型的評價標準

支持向量機回歸預測模型的訓練精度由均方誤差MSE和平方相關系數r2評價，其公式如下所示：

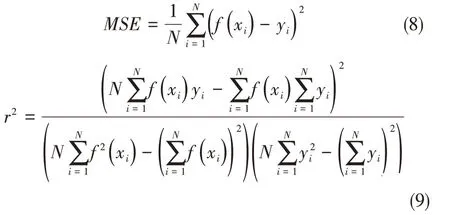
式中，N表示訓練集個數，yi表示實測值，f（xi）表示預測值。MSE越接近于0，r2越接近于1 說明模型的訓練精度越高。

磨削力變化趨勢預測模型的預測精度由相對誤差E衡量，由模糊粒子描述變化范圍，若磨削力的實際變化范圍為［a，m，b］，模型預測變化范圍為［ya，ym，yb］，則誤差E的公式為：

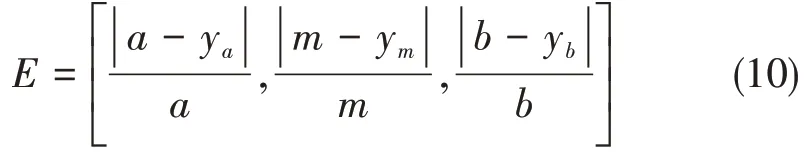
1.5 磨削力變化趨勢預測流程

將模糊信息粒化方法與人工免疫系統粒子群算法優化支持向量機回歸預測模型相結合，對超聲磨削氧化鋁陶瓷的磨削力變化趨勢進行預測，其原理如圖1所示。

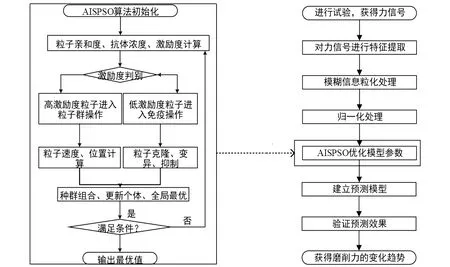
圖1 磨削力變化趨勢預測原理圖Fig.1 Schematic diagram of prediction of grinding force change trend

2 超聲磨削氧化鋁陶瓷實驗

2.1 裝置與方案

為獲得超聲磨削氧化鋁陶瓷中的磨削力變化趨勢，采用VMC850E 立式加工中心和聲學系統為主要設備搭建磨削試驗平臺，其中聲學系統由超聲波發生器、換能器、變幅桿及試件組成。試驗時，磨削力信號通過Kistle9257b 測力儀傳感器采集，測力儀的采樣頻率設置為30 kHz，超聲振幅由KEYENCE 激光位移傳感器測量儀測定，試件沿著變幅桿方向做縱向振動，砂輪對試件端面進行平面磨削，工藝參數及其他試驗條件如表1所示。

2.2 結果分析

對測力儀采集的磨削力信號進行處理，從中提取出砂輪切入至砂輪完全切出這一時段的磨削力信號，信號中包含有時間、切向力、法向力以及徑向力，本文選取時間和法向磨削力（下文簡稱磨削力）作為研究對象。

表1 超聲磨削試驗條件Tab.1 Conditions of ultrasonic grinding test

因磨削力信號的采集頻率較高，導致采集的點數較多，不利于磨削力變化趨勢分析，所以根據砂輪轉速計算出砂輪旋轉一周所需要的時間，以砂輪旋轉一周的時間為采樣周期，取每個周期的平均值作為磨削力的時間序列，則共有85 組數據。提取的磨削力時間序列如圖2所示。

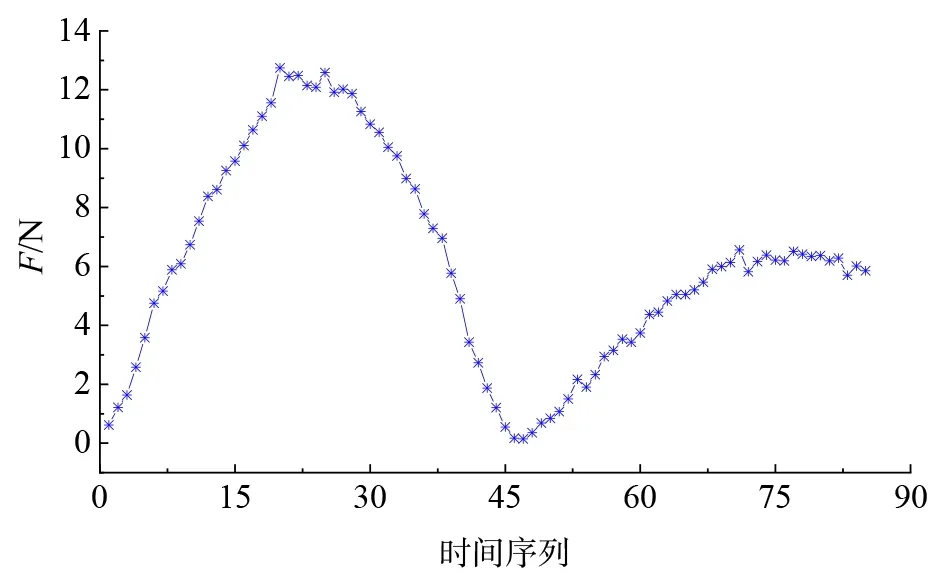
圖2 磨削力的時間序列Fig.2 Series of grinding force time

從圖2可知，磨削力呈現兩段先增大后減小的變化趨勢，且第二段增長趨勢變緩。這是因為試驗采用碗形砂輪，當砂輪運動到中間時會與試件分離，導致磨削力降到最低，接著砂輪再次磨削試件，但試件已經經過多次磨削，表面較為平整，再次磨削時磨削力會大幅減低。

3 超聲磨削氧化鋁陶瓷的磨削力變化趨勢預測

3.1 磨削力的模糊信息粒化

將85組磨削力數據進行劃分，前80組作為訓練集，后5組作為測試集，并根據三角形模糊粒子對訓練集進行信息粒化處理，粒化窗口大小設置為5，共有16個窗口。磨削力的模糊信息粒化結果如圖3所示。第16個窗口由模糊粒子描述的磨削力變化范圍為［6.175 1 6.366 7 6.502 3］。由圖3可以看出，三角形模糊粒子很好地模擬了磨削力的變化趨勢。。

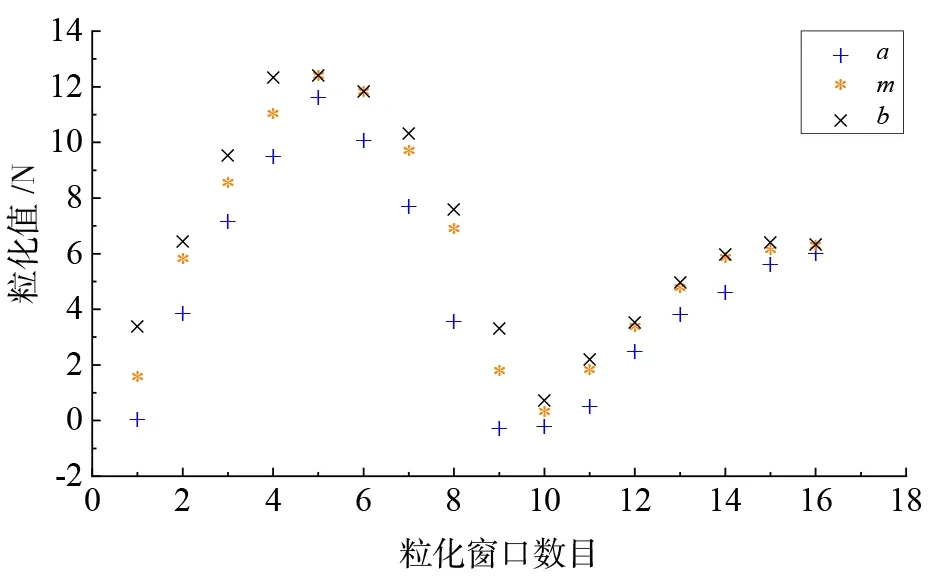
圖3 磨削力的粒化結果圖Fig.3 Graph of grinding force granulation results

3.2 SVM回歸預測模型的參數優化及其評價

將AISPSO 算法進行初始化，并對SVM 的懲罰參數C和核參數γ進行迭代尋優，其適應度設置為k折交叉驗證誤差最小，其中k折交叉驗證指將數據分為k組，每次將k-1 組作為訓練集，剩余一組作為測試集，循環k次，將這k組模型的預測精度的平均值作為訓練精度，本文k取5。

為使AISPSO 算法的尋優精度更高，將算法的進化代數設置為500，種群最大數量設置為50，SVM 的懲罰參數C和核參數γ的尋優范圍設置為［2-7，210］，其他參數設置如表2 所示。三個模糊粒子參數的SVM回歸預測模型參數優化結果如表3所示。

將上述通過AISPSO 算法優化的最優懲罰參數C和核參數γ用于SVM 模型訓練，得到的訓練結果如圖4所示，使用均方誤差MSE和平方相關系數r2對模型進行評價，其結果如表4所示。從表4可知，a，m，b三個參數的SVM 回歸預測模型精度較高，模型均方誤差MSE最小可達0.013 513，平方相關系數r2最大可達0.999 857；從圖4中可以看出，預測模型能夠實現對訓練樣本的精確模擬。

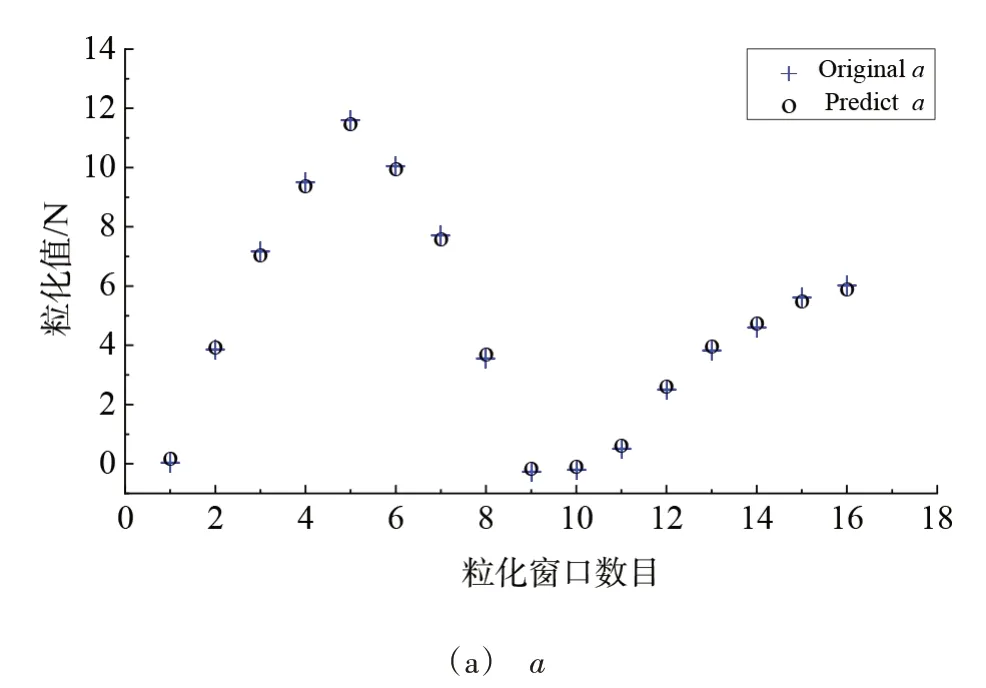
表2 AISPSO算法參數設置Tab.2 AISPSO algorithm parameter settings

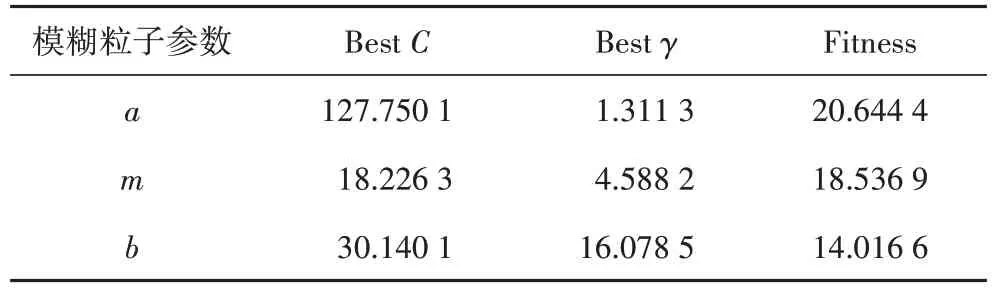
表3 SVM模型參數優化結果Tab.3 Results of SVM model optimization

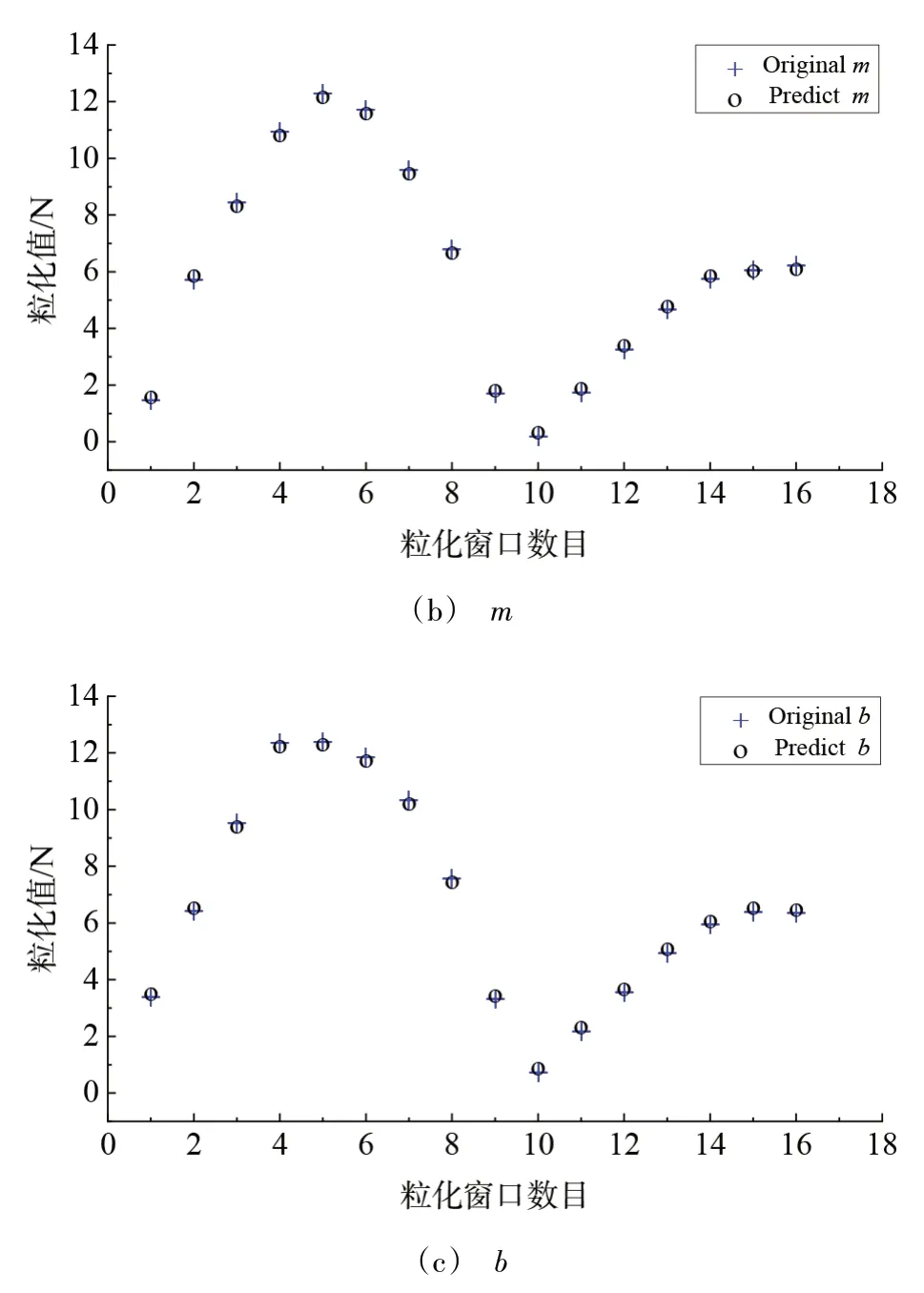
圖4 SVM模型訓練結果Fig.4 Results of SVM model training

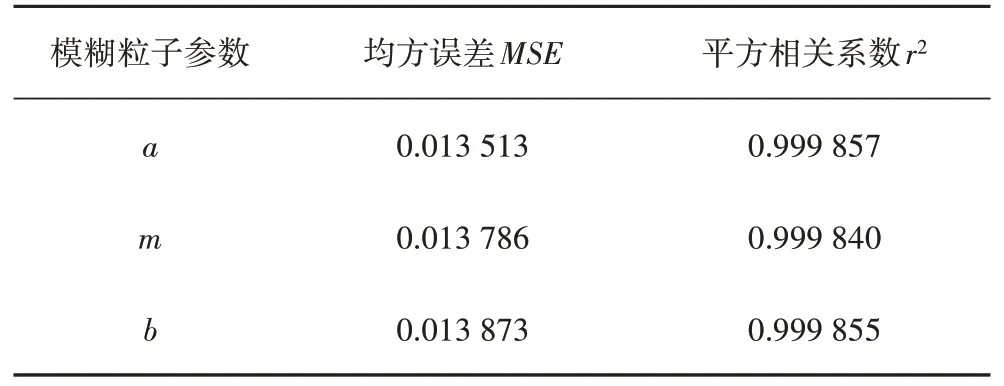
表4 模型均方誤差和平方相關系數Tab.4 Model mean square error and square correlation coefficient

3.3 基于SVM回歸模型的磨削力變化趨勢預測

使用測試集對優化后的SVM 預測模型進行驗證，將訓練優化后的SVM 回歸預測模型用于預測未來一個模糊窗口（窗口大小為5），其結果如表5 所示，其中實測范圍值由編號為81～85的實測磨削力模糊信息粒化獲得；預測范圍值由表3 得到的SVM 模型預測獲得；預測相對誤差E由公式（10）獲得。

從表5 中可以看出，預測的未來5 組磨削力變化范圍誤差在10%以內，與前5組（圖3第16窗口）磨削力數據相比，磨削力有變小的趨勢。加工時可根據磨削力變化趨勢即時對工藝參數進行調整，以獲得更好的表面質量。

3.4 改變周期大小

探究在磨削力信號特征提取時周期大小對模型精度的影響。分別選取砂輪旋轉1周、2周、3周、4周的時間作為采樣周期，粒化窗口大小設置為3，其他條件不變，不同周期大小預測模型的相對誤差如表6所示，其中預測相對誤差E由公式（10）獲得。

從表6 中可以發現，當周期逐漸變大時，預測相對誤差變大，預測精度逐漸降低，3 周之后精度則無法保證，這是由于周期變大提取特征中有效信息嚴重丟失，使算法預測效果變差。

4 結論

（1）基于模糊信息粒化方法和人工免疫系統粒子群算法優化支持向量機回歸預測模型，實現了對超聲磨削氧化鋁陶瓷的磨削力變化趨勢及變化范圍預測，且預測的磨削力變化趨勢相對誤差在10%以內。

（2）采用改進的人工免疫系統粒子群算法優化支持向量機回歸預測模型，提高了預測模型的訓練精度，其模型均方誤差MSE最小可達0.013 513，平方相關系數r2最大可達0.999 857。

（3）對磨削力信號特征提取時的周期大小選擇進行了討論，得到以砂輪旋轉1周的時間作為采樣周期時，能獲得較高精度。

表5 磨削力的變化趨勢及變化范圍Tab.5 Change trend and range of grinding force

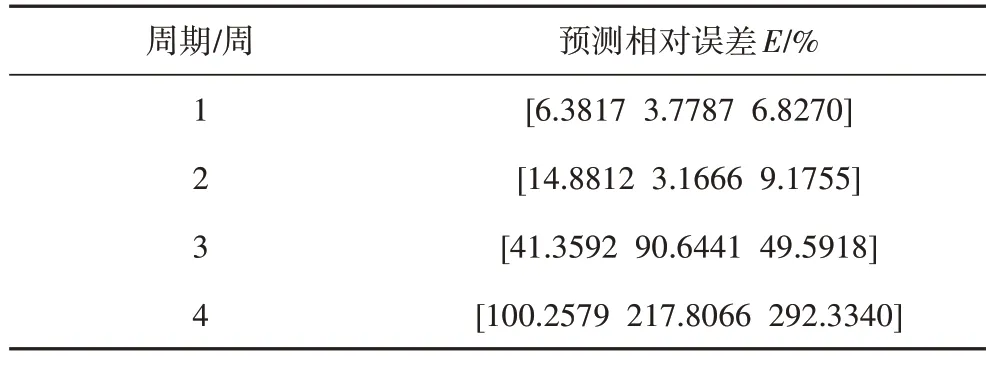
表6 磨削力不同周期的預測相對誤差Tab.6 Relative error of grinding force prediction in different periods