港池長周期波浪振蕩模態研究

劉遠超,袁博博,于 倩

(1.河海大學 港口海岸與近海工程學院，南京 210098； 2.中國港灣工程有限責任公司，北京 100027； 3.華北水利水電大學 環境與市政工程學院，鄭州 450046)

在港口的建設中，往往修建防波堤對港域水體進行掩護。然而當外海波浪周期較長時，其掩護效果并不直觀。并且當外海長周期波浪的頻率與港口自身固有頻率比較接近時，港域水體易發生強迫振動，港域波高幅值將劇烈上升，其振幅可達到入射波浪振幅的數倍，從而發生港口共振[1]，進而危害港域泊穩條件。

20世紀50年代開普敦港口發生嚴重的假潮振蕩事故，國外學者開始針對港口的長波和假潮開展研究。Botes[2]等人根據南非港口20世紀70年代末和20世紀80年代初的數據，對長波的起源和產生機制進行研究，并根據經驗得出長波與熱帶氣旋之間的關系。Hwang和Tuck[3]通過求解奇異積分方程，研究了恒定水深任意形狀與尺度港口的港池振蕩。Heneik[4]等人利用物理模型試驗模擬貝魯特港內波浪分布及破碎情況，并用非線性Boussinesq模型研究港內長波增長及空間變化，結果發現物理模型與數值模型結果吻合良好，港內長波能量主要集中在50～80 s和6～7 min，二者分別對應于港池的自然模態和赫爾姆霍茨模態，該方法可為后續風浪和涌浪作用下的港池低頻振蕩研究提供參考。Duncan Stuart[5]基于恩瓜拉港(Port of Ngqura)船舶劇烈運動和系泊事故，基于實測數據和MIKE21-BW模型研究了港內長波的產生、侵入和共振現象。王崗[6]基于線性假定，給出了狹長矩形港灣縱向振蕩的解析表達。史力生和潘軍寧[7]基于濱海核電站取水口工程的波浪整體模型試驗，分析了取水明渠內長周期波動產生的條件及影響因素。馬小舟、劉嬪[8-9]等人采用Boussinesq波浪數值模型模擬了孤立波，模擬了不同波高的孤立波分別對常水深和變水深細長港作用時港內的響應。史宏達、徐國棟[10-11]等人利用Boussinesq波浪數值模型針對理想地形下的港池不同入射波周期的港內波高進行計算，預測港內振蕩的發生，進而提出預防措施。馮海暴[12]、喬吉平[13]等人結合實測資料，研究了長周期波作用下港域長周期波浪分布規律和打樁船作業存在的問題，并提出相應的防治措施。盡管很多學者針對長周期波浪開展了研究，但是很多研究尚停留在特定理想港池的長波振蕩情況，因此本文采用數值模擬方法，研究某核電港域的長周期波浪振蕩頻率，并對港內長周期波浪的振蕩模態進行了分析。

1 模型驗證

1.1 模型簡介

MIKE21-BW波浪數值模擬模型由丹麥水利研究所開發，該模型基于Madsen和S?rensen[14-15]提出的改進頻散關系和變淺性能的Boussinesq方程，采用交替方向隱格式(ADI)進行時域內的求解。經過長期發展，BW模型不僅可以較好地描述近岸水域波浪傳播過程中發生的折射、繞射、反射和非線性波-波相互作用，而且還可以推廣至研究破碎區和上爬區的波浪現象。其控制方程和數值計算方法可參見文獻[14-15]。

1.2 模型驗證

本文結合某核電廠局部波浪整體物理模型試驗，驗證數值模型的合理性，圖1和表1分別為試驗中模型布置圖和波浪要素，測點具體布置參見圖2。核電廠海工工程規劃方案的平面布置包括取水明渠、排水明渠、大件碼頭、護岸和干施工圍堰，各分項工程平面規劃方案如下：取水明渠由南北兩條取水堤環抱而成，口門朝向NNE，兩堤堤頭相距240 m，取水南堤堤頂高程為12 m。排水明渠分兩期建設，其中一期工程包括東西兩條排水堤，口門朝向SSE，兩堤堤頭相距190 m，排水東堤高程為11 m。北部護岸擋浪墻頂高程為16 m。SE和SSE方向參見圖1。

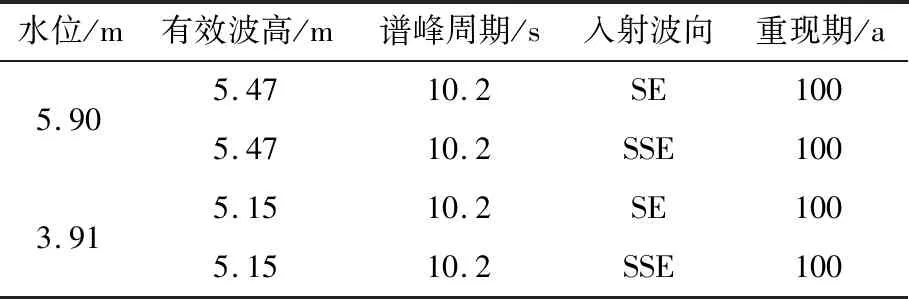
表1 試驗波要素Tab.1 Wave element in physical model test

物理模型試驗在40 m×60 m×1.5 m的波浪港池中進行，港池一端裝有多向不規則波造波機系統，可按要求模擬規則波和各種譜型的不規則波，港池四周裝有消浪設施以減小波浪的二次反射，波高采用DJ-800型多功能數據采集、處理及分析，實驗比尺為1：80。

數值模型完全參照物理模型平面布置(圖1)設定，將物理模型試驗的平面布置以及試驗水池按照試驗比尺1：80進行同比放大，得到港域地形數值模型圖。波浪數學模型的計算范圍是1 600 m×5 000 m，地形設置與物理模型完全相同，即港外高程-11 m、港內高程-9 m，模型的空間步長采用10 m。波浪完全采用物理模型試驗的波要素，按試驗比尺1：80同比放大后，生成造波文件，輸入到造波線，波浪的時間步長和模擬時間與物理模型試驗一致。為確保波浪傳播穩定，對模型兩側固壁邊界采用全反射。由于港域所有防波堤型式均是斜坡式結構，扭王字塊進行護岸，采用部分反射，從而較好地模擬扭王字塊的消波作用。由于模型主要模擬港域的長周期波浪振蕩情況，故而在海綿層的設置中注重吸收長周期波浪。在模型的開邊界海綿層的厚度均設置了100層，即海綿層的厚度達到1 000 m，從而最大程度吸收長周期波浪。

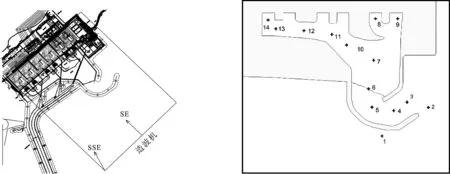
圖1 模型布置圖 圖2 測點布置圖Fig.1 The model layout Fig.2 The measuring point layout

由于本文的研究重點是長周期波浪，因此著重驗證MIKE21-BW模型對長周期波浪的模擬情況，分別對港池內長周期波浪的波高與周期進行驗證。利用傅立葉變換進行濾波處理，低通濾波器的截止頻率為0.033 Hz(對應波浪周期為30 s)，即30 s以上的波浪定義為長周期波浪。

1.2.1 波浪波高驗證

利用傅立葉變換分離長周期波浪序列，將長周期波浪的有效波高與物理模型試驗中的長周期波浪有效波高進行對比，得到如圖3所示港域測點數值模型與物理模型波高對比圖。可見，各測點總波高和長周期波高數值模擬結果和物理模型試驗結果吻合度較高，總體驗證結果良好。

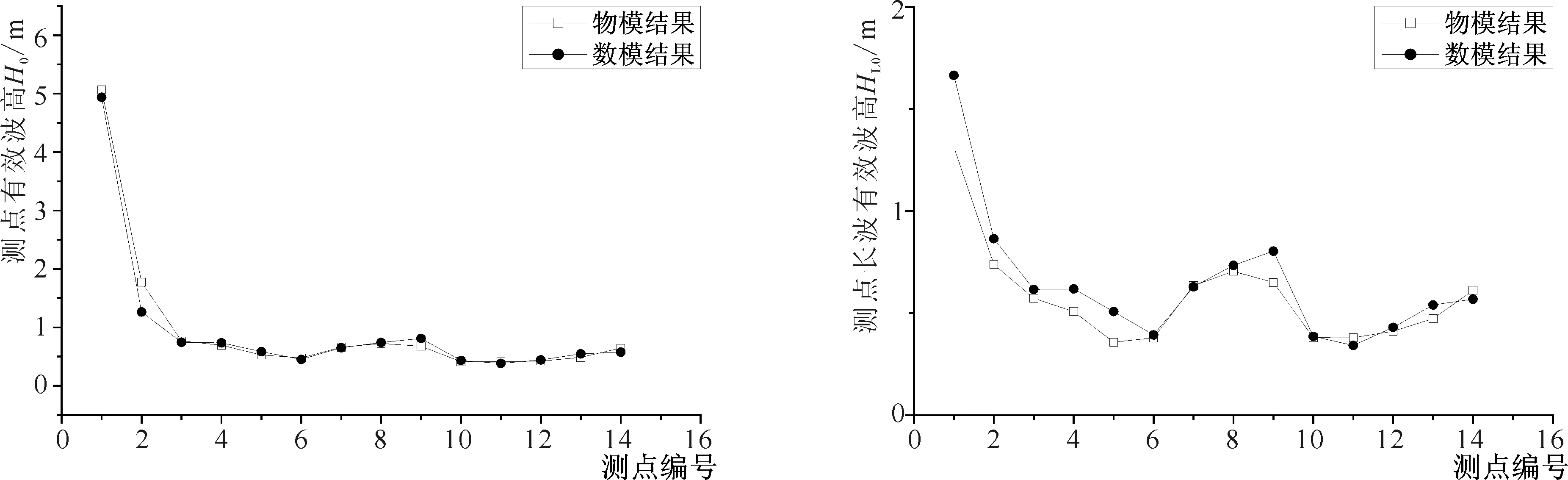
3-a 入射波向SE，HS=5.15 m

1.2.2 波浪周期驗證

利用傅立葉變換分離出各測點的長周期波浪，統計長周期波浪的振幅頻率圖，其對比結果參見圖4。鑒于測點數量較多，本文選取8和13兩個典型測點的波浪進行對比。在各組工況下，港內各測點波浪周期的數值模擬結果和物理模型試驗結果吻合度較高，總體驗證結果良好，即數值模擬計算結果可以較好模擬港池長周期波浪振蕩情況。

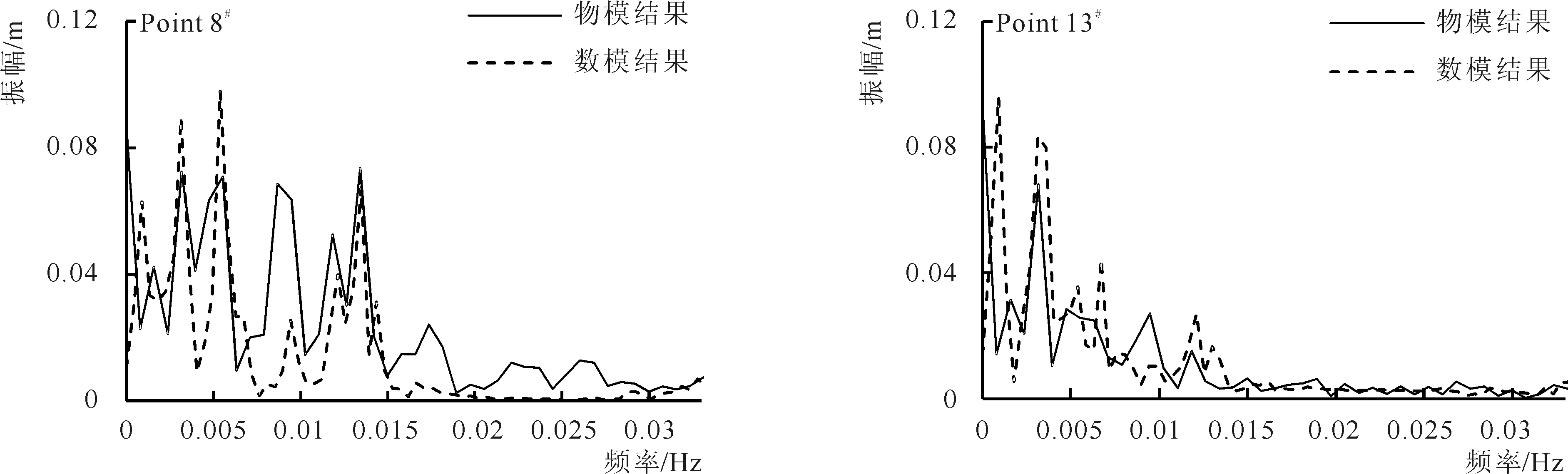
4-a 入射波向SE，HS=5.15 m

2 港池的固有頻率

為進一步了解港池的共振模態和對應頻率，本文采用白噪聲進行研究。本文白噪聲的時間序列共模擬10 000 s，時間步長取0.1 s。入射波向為SE向，波浪以單向波的形式傳入港域，各個頻率下波浪的振幅均為0.000 5 m。計算結果統計不同測點的波面時間過程，將30 s以上的波浪定義為長周期波浪，對應頻率為0.001～0.033 Hz。

圖5展示了港內測點和入射白噪聲波序列的幅頻對比圖，在港內選取特征點9和14進行對比分析。在白噪聲波序列的作用下，港池發生了明顯的長周期振蕩，港內測點9在600～850 s、250～320 s、130～170 s、66～72 s、53～55 s所對應的頻率下均發生了明顯的港灣共振，在600～850 s的長周期波浪振蕩幅度為0.002 4 m，達到入射波浪振幅的5倍。測點14在600～850 s、250～320 s、130～170 s、77～80 s、36～39 s所對應的頻率下均發生了明顯的港灣共振。在600～850 s的長周期波浪振蕩幅度為0.003 3 m，達到入射波浪振幅的6.6倍。由于測點9和14在600～850 s、250～320 s、 130～170 s區間均發生明顯的波能放大現象，因此該部分區間對應于港池的固有頻率。而在測點9出現了66～72 s、53～55 s的長周期波浪振蕩，測點14出現了77～80 s、36～39 s的長周期波浪振蕩，這可能是由于港池的不規則導致，屬于港池內部的局部長波振蕩。

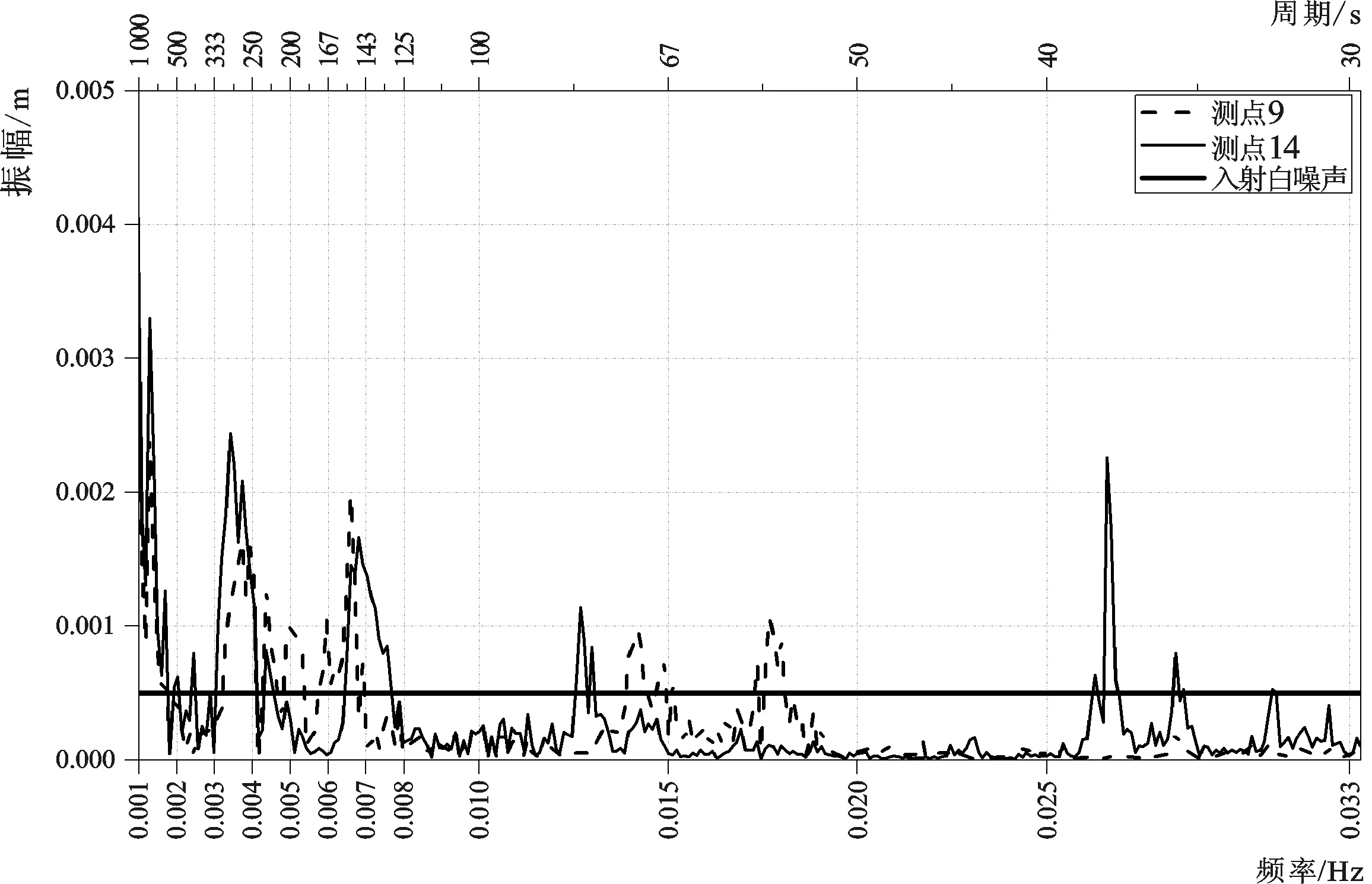
圖5 白噪聲誘導下長波振幅頻率圖Fig.5 The long-period wave amplitude-frequency under white noise

3 港池長波振蕩模態

根據白噪聲的探測結果，可以找到港池長周期振蕩的頻率區間以及放大倍數，然而對于港池的固有頻率的具體值和長周期波浪振蕩模態尚不清晰，因此本文設置一系列規則波，研究各個規則波作用下港池的長周期振蕩模態，入射波向采用SSE向，規則波的波高均設置0.01 m，周期取值采用白噪聲計算結果中發生長周期振蕩的對應區間，即600～850 s、250～320 s、130～170 s對應區間。

3.1 600～850 s波浪振蕩模態

入射波要素采用600～850 s區間內的一系列規則波，計算時長取80 000 s，探測長周期波浪振蕩的最大幅值，從而鎖定港池固有頻率。在830 s附近時港池長周期振蕩波高顯著，對830 s附近周期進行局部加密后輸入到模型中，發現833 s的長周期波浪計算結果最大，因此833 s對應于港池的固有頻率。在833 s的長周期規則波作用下，港內波高明顯被放大，最大波高達到0.053 m，超過入射波高的5倍，計算結果見圖6。根據圖6-a的計算結果，從港池左側取水口到港池外部口門，即圖中的A-B斷面，波浪的波面高度逐漸減小，即833 s長周期波浪振蕩模式是以口門B為波節，港域內部邊界A為波腹的長周期振蕩，此時長周期波浪的1/4波長與港域的尺度相當，該振蕩模式稱為Helmholtz模式。該模式引起的波浪振幅放大幅度最為劇烈，為港池振蕩的第一模態。

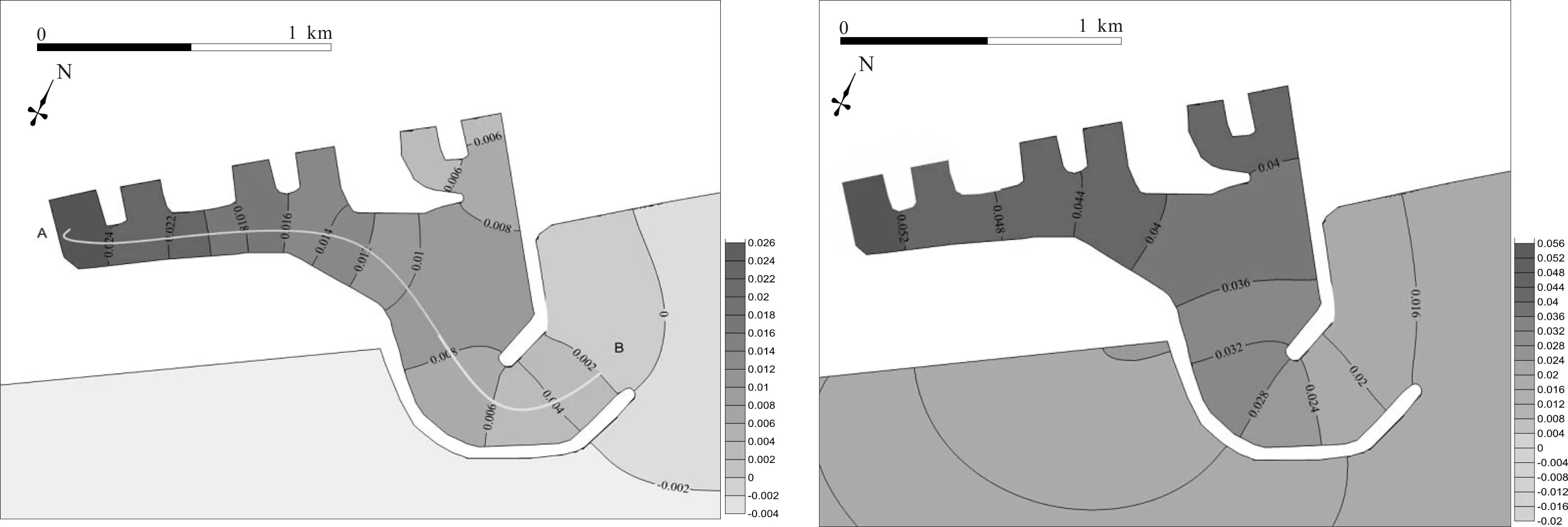
6-a t=40 000 s波面高度 6-b 港內波高計算結果

3.2 250～320 s波浪振蕩模態

在250～320 s區間內設置一系列周期的波浪輸入到模型中，計算時長為30 000 s，發現在300 s時港內的長周期波浪振蕩尤為顯著，因此300 s對應于港池的固有頻率。計算結果見圖7，可以看到港內波高明顯被放大，最大波高達到0.046 m，達到入射波高的4.6倍。根據圖7-a的計算結果，從港池左側取水口到港池右部邊界，即圖中的A-B斷面，A處波面位于最高位置時，B處波面位于最低位置，A、B兩處均是波腹，即波浪的振蕩模式是以港池內部A和B為波腹，C處為波節的長周期振蕩，此時長周期波浪的1/2波長與港域的橫向尺度AB相當，其對應于港池長周期波浪振蕩的第二模態。

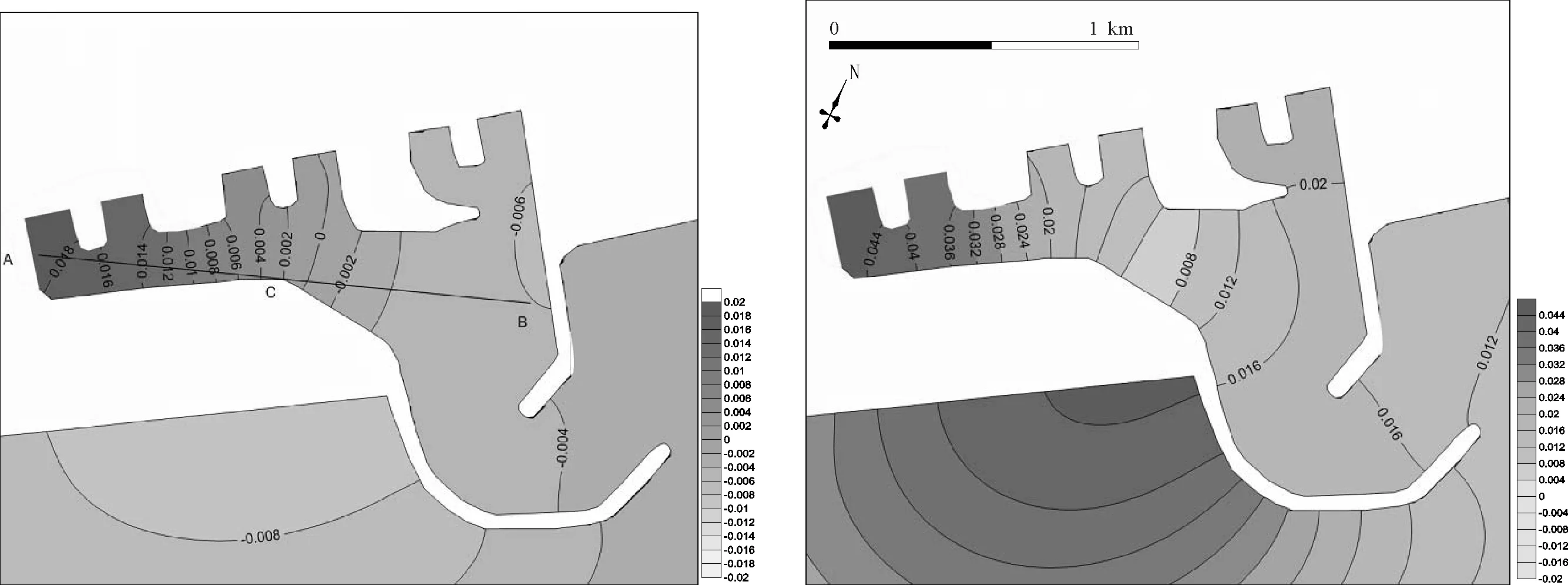
7-a t=18 000 s波面高度 7-b 港內波高計算結果

3.3 130～160 s波浪振蕩模態

入射波要素采用130～160 s區間內的一系列規則波，計算時長取30 000 s，探測長周期波浪振蕩的最大幅值，從而鎖定港池固有頻率。在150 s附近時港池長周期振蕩波高顯著，對150 s附近周期進行局部加密后輸入到模型中，發現151 s的長周期波浪計算結果最大，因此151 s對應于港池的固有頻率。計算結果參見圖8，港內左側取水口A處和中部取水口C處波高均明顯被放大，最大波高分別達到0.045 m和0.046 m，達到入射波高的4.5倍和4.6倍。根據圖8-a的計算結果，從港池左側取水口到港池右側，即圖中的A-B斷面， A處波面位于最低位置時，D處波面正好處于水平位置，C處波面正好位于最高位置，港池右側B處波面位于水平位置，其振蕩模式是以港池內部A和C為波腹，B和D為波節的長周期振蕩，此時長周期波浪的3/4波長與港域的橫向尺度AB相當，對應于港池第三模態。

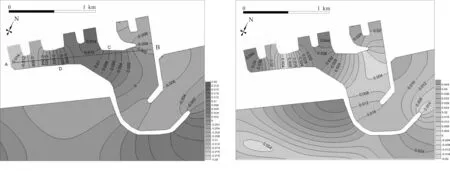
8-a t=24 000 s波面高度 8-b 港內波高計算結果

4 小結

本文依據某核電港池物理模型項目的試驗結果，驗證BW數值模型的合理性。基于數值模型利用白噪聲波浪信號探測港池的固有頻率，并分別利用微幅規則波研究港內各水域的波面變化情況和港域長周期波浪的振蕩模態。具體結論如下：

(1)基于MIKE21-BW模型計算港域長周期波浪的波高分布和頻率分布情況，并與整體物理模型試驗結果進行對比分析，二者吻合良好，驗證了BW模型計算港內波浪的合理性。

(2)在白噪聲波序列的作用下，港池發生了明顯的長周期振蕩，在600～850 s、250～320 s、130～160 s幾個主要頻率區間內均發生了明顯的港灣共振，其中600～850 s對應的長周期波浪振蕩幅度最大達到0.003 3 m，為入射波浪振幅的6.6倍。

(3)600～850 s、250～320 s、130～170 s幾個主頻下分別對應于港池的第一、第二、第三模態，港域的尺度分別與600～850 s波浪的1/4波長、250～320 s波浪的1/2波長、130～170 s波浪的3/4波長趨于一致。