基于粒子群優(yōu)化算法的碳纖維紗線用編織錠子結(jié)構(gòu)參數(shù)的優(yōu)化
楊曉東,孫志軍,杜誠(chéng)杰,葉 超
(東華大學(xué) 機(jī)械工程學(xué)院,上海 201620)
碳纖維作為一種新型高分子無(wú)機(jī)材料,因其耐腐蝕、耐高溫、高強(qiáng)度、可編織和輕量化,常與編織工藝相結(jié)合制成碳纖維預(yù)制件[1]。隨著復(fù)合材料的發(fā)展,通過現(xiàn)代工藝獲得的碳纖維增強(qiáng)預(yù)成型件被廣泛應(yīng)用于航空航天、汽車制造等領(lǐng)域,由于碳纖維增強(qiáng)預(yù)成型件的廣闊應(yīng)用前景,許多專家學(xué)者對(duì)碳纖維編織進(jìn)行了相關(guān)研究[2-3]。編織錠子作為碳纖維編織機(jī)中的重要組成部分,在編織過程中,編織錠子通過自身補(bǔ)償碳纖維紗線長(zhǎng)度,以確保碳纖維紗線張力穩(wěn)定并滿足加工要求。編織過程中碳纖維紗線張力波動(dòng)對(duì)于碳纖維編織件品質(zhì)影響非常大,碳纖維紗線會(huì)因紗線張力波動(dòng)大,導(dǎo)致碳纖維單絲在變應(yīng)力作用下發(fā)生斷裂產(chǎn)生編織起毛問題。
為了降低編織錠子放紗階段紗線張力波動(dòng),使碳纖維紗線在合適的編織張力下完成編織,需要對(duì)編織錠子的結(jié)構(gòu)參數(shù)進(jìn)行優(yōu)化,但國(guó)內(nèi)關(guān)于編織錠子方面的研究較少。王晗等[4]分析了影響紗線張力波動(dòng)的因素,提出修改棘輪棘爪制動(dòng)為摩擦制動(dòng)以降低放紗階段紗線張力波動(dòng);李榮林[5]為了提高鋼絲編織膠管的品質(zhì),設(shè)計(jì)了鋼絲編織摩擦錠子;扈昕瞳等[6]研究了不同放線速度對(duì)紗線張力波動(dòng)的影響,證明了編織錠子快速放線可以縮小紗線張力波動(dòng)范圍;邢圓圓[7]、李宗迎[8]、賀辛亥等[9]都針對(duì)變截面三維編織方面進(jìn)行了研究,并設(shè)計(jì)出了主動(dòng)增減紗攜紗器用于生產(chǎn)變截面三維編織預(yù)制件。 MA等[10]分析并建立了杠桿式編織錠子的紗線張力模型,同時(shí)研究了不同彈簧剛度條件下的紗線張力波動(dòng)變化情況。ZHANG等[11]針對(duì)普通曲折法編織錠子進(jìn)行了局部?jī)?yōu)化,并根據(jù)多剛體動(dòng)力學(xué)理論建立了相應(yīng)的紗線張力模型,所得仿真結(jié)果紗線張力波動(dòng)優(yōu)于普通曲折法編織錠子。
本文以自主設(shè)計(jì)的碳纖維紗線用編織錠子為基礎(chǔ),首先介紹花柱編織工藝和碳纖維紗線用編織錠子結(jié)構(gòu),并分階段建立紗線張力模型;其次介紹粒子群優(yōu)化算法原理,根據(jù)優(yōu)化目標(biāo)選擇結(jié)構(gòu)參數(shù)和優(yōu)化目標(biāo)函數(shù)并確定結(jié)構(gòu)參數(shù)優(yōu)化范圍;最后確定粒子群優(yōu)化算法參數(shù),使用MatLab軟件完成碳纖維紗線用編織錠子結(jié)構(gòu)參數(shù)優(yōu)化,并將優(yōu)化結(jié)果與優(yōu)化前和單補(bǔ)償編織錠子實(shí)驗(yàn)結(jié)果比較,從而探求編織錠子結(jié)構(gòu)參數(shù)優(yōu)化對(duì)于紗線張力波動(dòng)的影響。
1 碳纖維紗線用編織錠子紗線模型
1.1 花柱編織工藝與編織錠子結(jié)構(gòu)
1.1.1 花柱編織工藝
在編織機(jī)底盤平面上有8個(gè)轉(zhuǎn)度盤,每個(gè)轉(zhuǎn)度盤有4個(gè)撥槽,編織錠子按照1F1E(2個(gè)編織錠子之間間隔1個(gè)空位)的方式安裝在底盤平面上。在編織過程中,編織機(jī)驅(qū)動(dòng)16個(gè)編織錠子隨著轉(zhuǎn)度盤沿著“8”字路徑運(yùn)動(dòng),根據(jù)編織錠子的運(yùn)動(dòng)方向一般分為2組,一組順時(shí)針運(yùn)動(dòng),一組逆時(shí)針運(yùn)動(dòng),2組編織錠子釋放的紗線重疊纏繞在芯模表面形成編織件。花柱編織工藝圖見圖1。
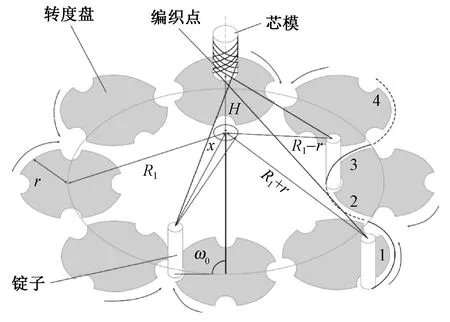
圖1 花柱編織工藝圖
在編織過程中,編織錠子出紗口與編織點(diǎn)之間紗線段長(zhǎng)度隨編織錠子運(yùn)動(dòng)不斷變化,為準(zhǔn)確求出編織錠子每個(gè)時(shí)刻出紗口紗線速度,以位置3作為編織錠子運(yùn)動(dòng)起點(diǎn)為例,根據(jù)編織機(jī)基本參數(shù)和轉(zhuǎn)度盤角速度可得編織錠子出紗口與編織點(diǎn)之間紗線段長(zhǎng)度變化表達(dá)式:
(1)
式中:R1為轉(zhuǎn)度盤圓心到芯模圓心之間的水平距離,m;r為撥盤半徑,m;r0為芯模半徑,m;ω0為撥盤角速度,rad/s;t為時(shí)間,s;H為編織點(diǎn)與出紗口之間高度差,m;lc為出紗口到編織點(diǎn)之間紗線段長(zhǎng)度,m。
編織錠子出紗口與編織點(diǎn)之間紗線段長(zhǎng)度隨時(shí)間的導(dǎo)數(shù)可通過式(2)求得出紗口與編織點(diǎn)之間紗線長(zhǎng)度變化速度vc(m/s)。
(2)
由于編織錠子出紗口紗線速度與芯模移動(dòng)速度有關(guān),為了保證碳纖維紗線在芯模上以恒定的編織角纏繞,芯模的移動(dòng)速度與轉(zhuǎn)度盤的轉(zhuǎn)動(dòng)角速度之間存在一定關(guān)系,可根據(jù)芯模半徑(r0)和碳纖維紗線寬度dt(m)求得紗線覆蓋率100%條件下的編織角度β(rad)繼而求得芯模移動(dòng)速度v0(m/s)。
(3)
(4)
根據(jù)芯模移動(dòng)速度v0,可以求出纏繞在芯模表面的碳纖維紗線運(yùn)動(dòng)速度vx(m/s),綜合出紗口到編織點(diǎn)之間紗線段長(zhǎng)度變化速度vc,編織錠子出紗口紗線速度v(m/s)。出紗口紗線速度圖如圖2所示。可知,出紗口紗線速度的變化主要與編織錠子從最近端到最遠(yuǎn)端再到最近端這個(gè)機(jī)器循環(huán)的時(shí)間有關(guān),即轉(zhuǎn)度盤的轉(zhuǎn)速有關(guān),本文根據(jù)碳纖維編織機(jī)轉(zhuǎn)度盤轉(zhuǎn)速范圍選擇轉(zhuǎn)度盤轉(zhuǎn)速為π rad/s。
(5)
v=vc+vx
(6)
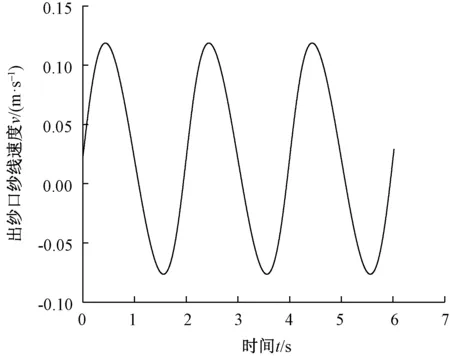
圖2 出紗口紗線速度圖
1.1.2 編織錠子結(jié)構(gòu)
碳纖維紗線用編織錠子結(jié)構(gòu)的出紗口、收放紗、紗線張力調(diào)控和紗線路徑與普通杠桿式編織錠子不同,是對(duì)碳纖維材料做的針對(duì)性優(yōu)化。編織錠子殼體上裝有橫軸1、2固定線墜,在線墜的另一端裝有滑輪4,在橫軸1下方有提桿與線墜一體。在橫軸2的上方安裝有彈簧3,利用彈力來(lái)限制橫軸2的運(yùn)動(dòng)。當(dāng)紗線被牽引出出紗口時(shí),線墜順時(shí)針旋轉(zhuǎn),彈簧1、2、3被壓縮,滑輪1、2分別向右、向左移動(dòng),提桿同時(shí)順時(shí)針旋轉(zhuǎn),最終提桿下端會(huì)與棘爪桿接觸并將其抬起,實(shí)現(xiàn)放紗。碳纖維紗線用編織錠子三維結(jié)構(gòu)軸測(cè)圖見圖3。
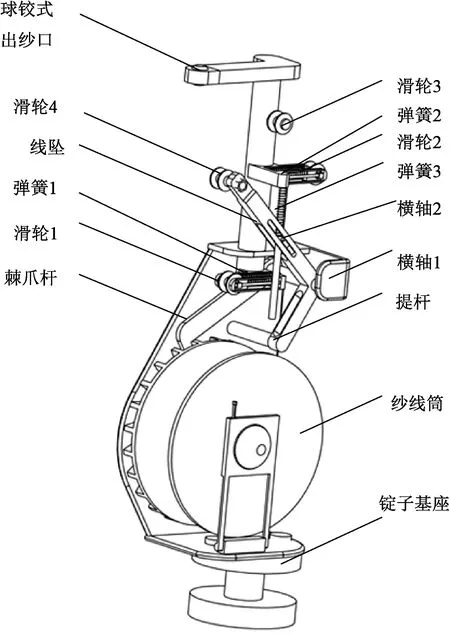
圖3 碳纖維紗線用編織錠子三維結(jié)構(gòu)軸測(cè)圖
1.2 編織錠子中紗線長(zhǎng)度計(jì)算
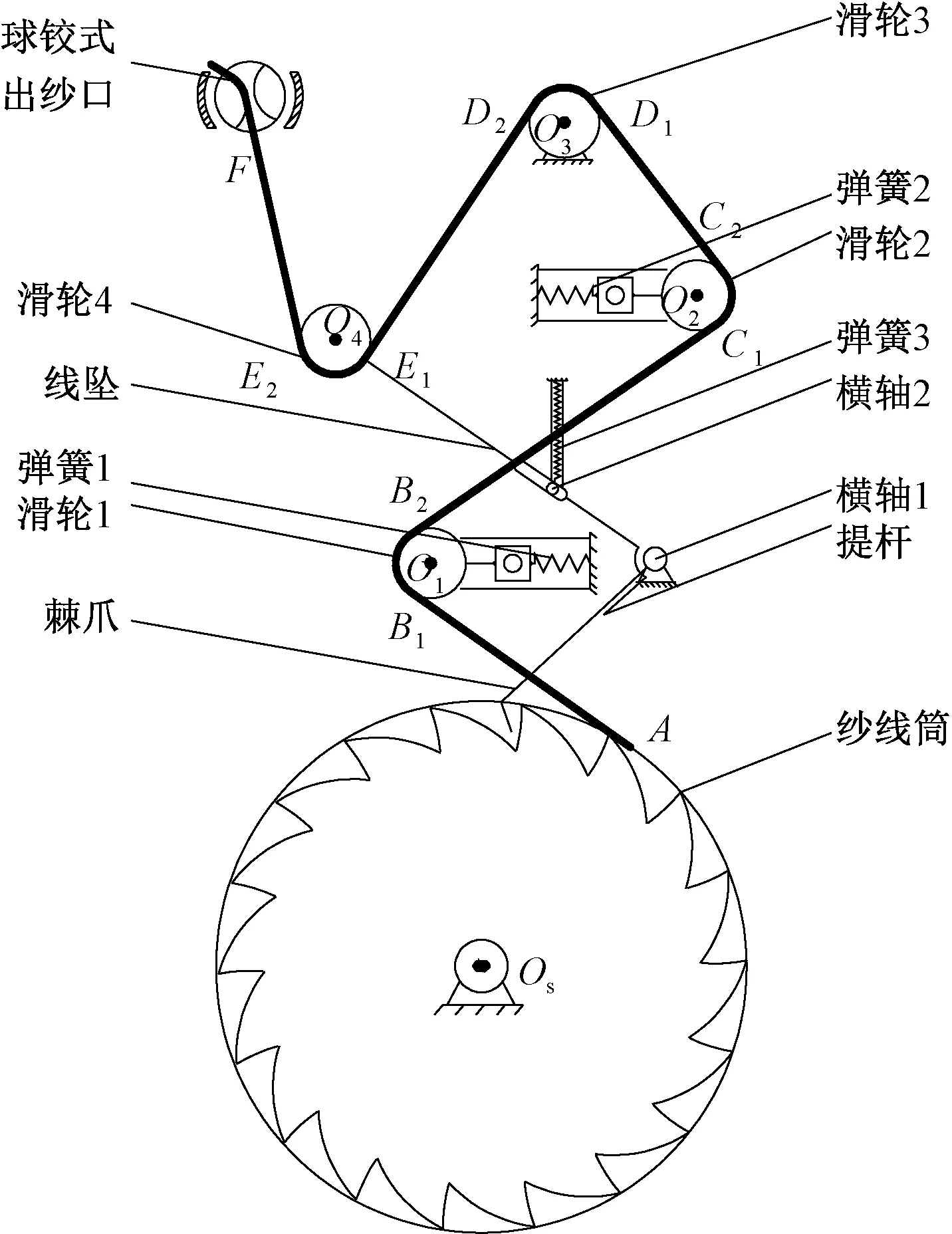
圖4 碳纖維紗線路徑圖
為了分析碳纖維紗線用編織錠子中紗線張力變化,首先需根據(jù)編織錠子結(jié)構(gòu),計(jì)算編織錠子中碳纖維紗線長(zhǎng)度變化。碳纖維紗線路徑圖見圖4。可以看出,A點(diǎn)為碳纖維紗線退繞點(diǎn);B1B2是纏繞在滑輪1上的碳纖維弧線段;C1C2是纏繞在滑輪2上的碳纖維弧線段;D1D2是纏繞在滑輪3上的碳纖維弧線段;E1E2是纏繞在滑輪4上的碳纖維弧線段;OS是紗線筒圓心;O1、O2、O3、O4分別是滑輪1、2、3、4的圓心;F為編織錠子出紗點(diǎn)。根據(jù)花柱編織工藝,在編織錠子運(yùn)動(dòng)過程中,出紗口與編織點(diǎn)之間紗線段與水平面之間的夾角隨著編織錠子的位置變化而變化,從而導(dǎo)致紗線與出紗口之間的包角隨之快速往復(fù)變化。為了改善該情況,碳纖維紗線用編織錠子中采用球鉸式出紗口調(diào)節(jié)紗線與出紗口之間的包角使其變化較小,減少其對(duì)紗線張力波動(dòng)的影響。為了準(zhǔn)確求出紗線與球鉸式出紗口之間的包角,需根據(jù)式(1)求出出紗口與編織點(diǎn)之間紗線段在水平面的投影距離lt,繼而求出紗線與球鉸式出紗口之間的包角φ(rad)。由于紗線與球鉸式出紗口之間包角隨時(shí)間變化不大,故假設(shè)球鉸式出紗口處紗線段長(zhǎng)度不變。為了簡(jiǎn)化模型計(jì)算,故將出紗點(diǎn)設(shè)為定點(diǎn)F。
(7)
(8)
在考慮紗線與碳纖維紗線用編織錠子路徑中各構(gòu)件之間包角變化的條件下,為了便于后續(xù)計(jì)算,將碳纖維紗線在退繞點(diǎn)A與出紗點(diǎn)F之間分為l1、l2和l3,以及紗線筒放紗量lf。當(dāng)線墜處于初始狀態(tài)時(shí)線墜旋轉(zhuǎn)角度為θmin。當(dāng)線墜旋轉(zhuǎn)角度為θmid時(shí),提桿與棘爪相接觸。當(dāng)線墜旋轉(zhuǎn)角度為θmax時(shí),棘爪桿離開棘輪,紗線筒開始放紗。當(dāng)線墜旋轉(zhuǎn)角度θmin<θ<θmax時(shí),l1、l2和l3的長(zhǎng)度發(fā)生變化。當(dāng)線墜旋轉(zhuǎn)角度θ>θmax時(shí),紗線筒釋放紗線并且l1、l2、l3和lf的長(zhǎng)度發(fā)生變化。因此,碳纖維紗線編織錠子工作過程分為2個(gè)階段,即紗線張力調(diào)節(jié)階段和紗線筒放紗階段,紗線張力調(diào)節(jié)階段又分為并聯(lián)彈簧作用和并聯(lián)彈簧與棘爪桿共同作用階段。
l1=lC1C2+lC2D1
(9)
l2=lAB1+lB1B2+lB2C1
(10)
l3=lD1D2+lE1E2+lD2E1+lE2F
(11)
(12)
式中:γ為紗線筒紗線纏繞角度,rad;α為紗線筒轉(zhuǎn)動(dòng)角度,rad;Rs為紗線筒半徑,m。
根據(jù)編織錠子幾何形狀、滑輪1、2、3、4圓心坐標(biāo)、紗線筒圓心坐標(biāo)和出紗點(diǎn)坐標(biāo),運(yùn)用勾股定理和2點(diǎn)之間距離公式得l1、l2、l3表達(dá)式為:
(13)
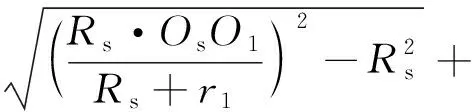
(15)
其中
(16)
式中:Oh為O2水平線與O3垂直線之間的交點(diǎn);r1為滑輪半徑,m;K為OhO2與OhO3的夾角,rad。
根據(jù)式(9)~(16)可求得l1、l2、l3和ls的變化。
(17)
1.3 編織錠子紗線張力模型
1.3.1 并聯(lián)彈簧作用階段
當(dāng)紗線逐漸被牽引出出紗口時(shí),線墜順時(shí)針旋轉(zhuǎn),線墜角度θmin<θ<θmid,屬于并聯(lián)彈簧作用階段,線墜受到滑輪4兩端作用于線墜的紗線張力分力T33(N)、T44(N),滑輪4重力G1(N),線墜重力G0(N)和彈簧3彈簧力F3(N)作用。其中T33為滑輪右側(cè)作用于線墜的紗線張力分力,T44為滑輪左側(cè)作用于線墜的紗線張力分力。當(dāng)線墜處于平衡狀態(tài)時(shí),T33與T44相等。并聯(lián)彈簧作用階段線墜受力分析圖見圖5。
(18)
F3=k3[Δs3+S3(tanθ-tanθmin)]
(19)
式中:l0為橫軸1圓心與滑輪4圓心之間的距離,m;lr為橫軸1圓心與線墜質(zhì)心之間距離,m;S3為橫軸1圓心與彈簧3之間的水平距離,m;k3為彈簧3的彈簧剛度,N/m;Δs3為彈簧3的預(yù)壓縮長(zhǎng)度,m;θ0為l0與lr之間的夾角,rad。
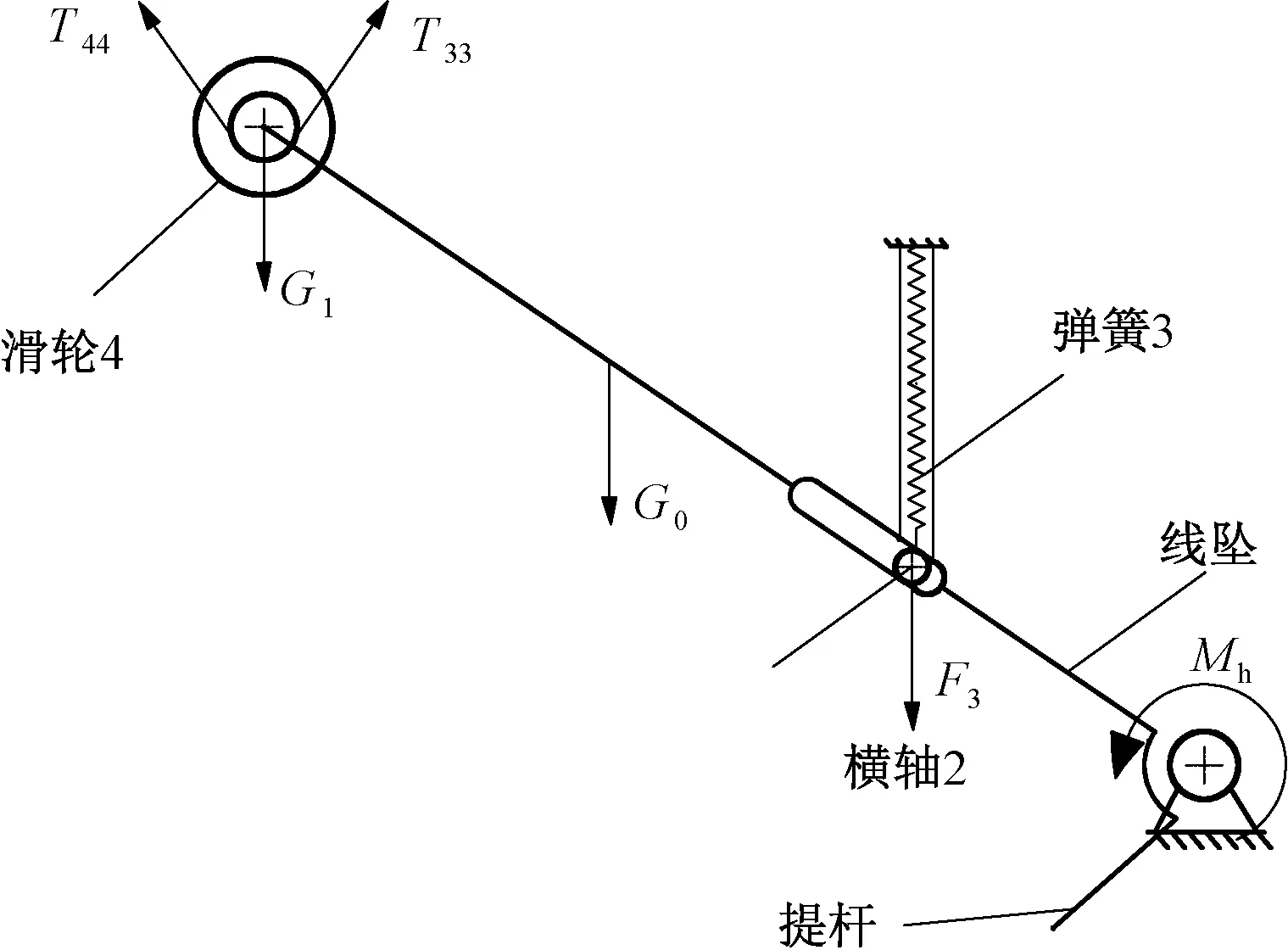
圖5 并聯(lián)彈簧作用階段線墜受力分析圖
根據(jù)式(9)~(17)采用微元法可得線墜轉(zhuǎn)動(dòng)的角速度和角加速度為:
(20)
(21)
由于橫軸1處線墜旋轉(zhuǎn)過程中會(huì)因摩擦產(chǎn)生摩擦力矩,故根據(jù)線墜構(gòu)件受力分析將線墜所受的所有力分解到水平和垂直2個(gè)方向,同時(shí)根據(jù)T33和T44與水平方向的夾角可得式(22)和式(23):
(22)
(23)
式中:Fhx為橫軸1施加在線墜上的水平分力,N;Fhy為橫軸1施加在線墜上的垂直分力,N;T44x為T44的水平分力,N;T44y為T44的垂直分力,N;T33x為T33的水平分力,N;T33y為T33的垂直分力,N;E0為滑輪4圓心O4的豎直線與滑輪4邊緣的交點(diǎn)。
繼而可根據(jù)式(18)~(23)建立線墜動(dòng)力學(xué)方程:
(24)
式中:Mh為橫軸1處摩擦力矩,N·m;J為線墜的轉(zhuǎn)動(dòng)慣量,kg·m2。
橫軸1處摩擦力矩為
(25)
式中:r3為橫軸1半徑,m;μh為橫軸1處摩擦因數(shù)。
線墜的轉(zhuǎn)動(dòng)慣量為
(26)
式中:ml為線墜的質(zhì)量,kg。
由于滑輪4兩端紗線張力還由彈簧1、2的彈簧力提供紗線張力分力,故需要對(duì)滑輪1、2進(jìn)行受力分析。滑輪1、2處受力分析圖如圖6所示,在紗線張力調(diào)節(jié)階段,紗線筒不放紗。根據(jù)式(27)、(28)可求得滑輪1下端紗線力Ttan1。
F1=k1[Δs1+S3tanθ-tanθmin]
(27)
(28)
式中:k1為彈簧1的彈簧剛度,N/m;Δs1為彈簧1的預(yù)壓縮長(zhǎng)度,m;F1為彈簧1施加的彈簧力,N。彈簧1、2受力分析圖見圖6。
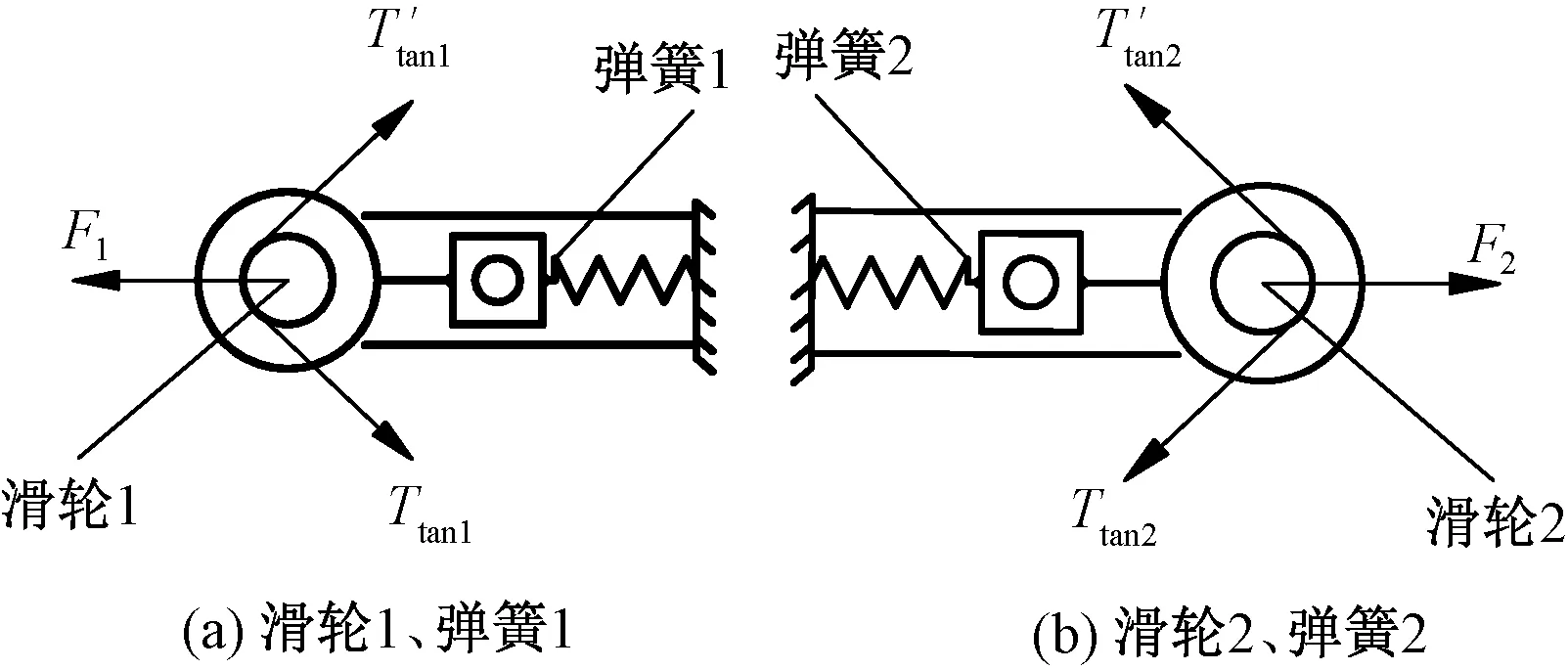
圖6 滑輪1、2和彈簧1、2受力分析圖
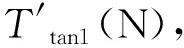
(29)
F2=k2[Δs2+S3(tanθ-tanθmin)]
(30)
(31)
式中:k2為彈簧2的彈簧剛度,N/m;Δs2為彈簧2的預(yù)壓縮長(zhǎng)度,m;F2為彈簧2施加的彈簧力,N;Tz為紗線輸出張力,N;Ts為紗線輸入張力,N;B為紗線彎曲剛度,N/m;μ為紗線與構(gòu)件之間的摩擦因數(shù);φ為紗線與構(gòu)件之間的包角,rad;Rq1為紗線在滑輪上的曲率半徑,m-1;μh為紗線與滑輪之間的摩擦因數(shù);kh為滑輪半徑與紗線在滑輪上曲率半徑的比值。
紗線繞過滑輪2和滑輪3后紗線張力變化可根據(jù)式(29)求得,結(jié)合線墜構(gòu)件受力分析中的T33,由式(33)求得滑輪4右側(cè)的紗線張力T3(N),繼而根據(jù)式(29),由式(34)(35)分別求得滑輪4左側(cè)紗線張力T4(N)和出紗口紗線張力T5(N)。
(35)
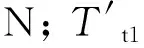
1.3.2 并聯(lián)彈簧與棘爪桿共同作用階段
當(dāng)紗線繼續(xù)被牽引出出紗口時(shí),線墜繼續(xù)順時(shí)針旋轉(zhuǎn),提桿逐漸帶動(dòng)棘爪桿離開棘輪,此時(shí)θmid<θ<θmax,并聯(lián)彈簧與棘爪桿共同作用階段線墜受力分析圖如圖7所示,圖中Fj為棘爪桿重力G2作用在提桿處的作用力,此時(shí)線墜構(gòu)件在多力作用下處于平衡狀態(tài)可得:
(36)
式中:lj為橫軸1圓心與棘爪桿質(zhì)心之間的距離,m;θj為提桿與線墜之間的夾角,rad;lt為橫軸1圓心與提桿與棘爪桿的接觸點(diǎn)之間的距離,m。
根據(jù)式(20)、(21)可得該階段線墜旋轉(zhuǎn)的角速度和角加速度,同時(shí)根據(jù)式(23)、(36)可得該階段線墜構(gòu)件的動(dòng)力學(xué)方程(37)(38)。并聯(lián)彈簧與棘爪桿共同作用階段線墜受力分析圖見圖7。
(37)
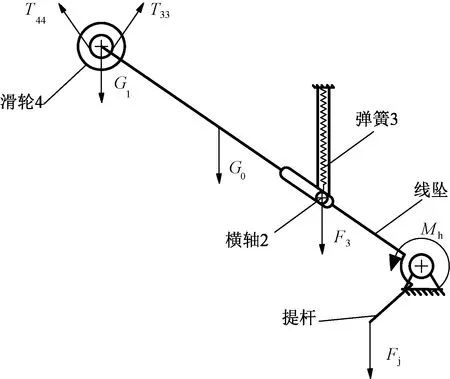
圖7 并聯(lián)彈簧與棘爪桿共同作用階段線墜受力分析圖
(38)
繼而根據(jù)式(27)~(35)求得T5。
1.3.3 紗線筒放紗階段
隨著紗線繼續(xù)被牽引出出紗口,此時(shí)線墜角度θ>θmax,棘爪桿離開棘輪,紗線筒開始旋轉(zhuǎn)放紗,隨后紗線張力迅速下降,棘爪桿同時(shí)逆時(shí)針旋轉(zhuǎn),當(dāng)線墜角度θ<θmax時(shí)棘爪桿迅速卡入下1個(gè)卡槽停止紗線筒旋轉(zhuǎn)。根據(jù)并聯(lián)彈簧與棘爪桿共同作用階段中求出的T5,根據(jù)式(29)可依次求出T4、T3、T2、T1和紗線筒處紗線張力T0,根據(jù)對(duì)紗線筒進(jìn)行受力分析可得紗線筒的動(dòng)力學(xué)方程為:
(39)
(40)
式中:ms為紗線筒質(zhì)量,kg;Is為紗線筒轉(zhuǎn)動(dòng)慣量,kg·m2;μs為紗線筒與軸摩擦因數(shù);Gs為紗線筒重力,N;Rr為紗線筒內(nèi)徑,m;Rs為紗線筒的外徑,m。
根據(jù)式(40)可求得紗線筒的角加速度,該階段碳纖維紗線長(zhǎng)度可根據(jù)微元法進(jìn)行計(jì)算。
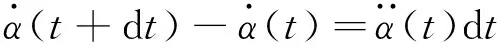
(41)
(42)
(43)
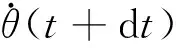
2 粒子群優(yōu)化算法
粒子群優(yōu)化算法是根據(jù)鳥類的飛行空間作為算法的解空間,根據(jù)種群中個(gè)體間的信息交流和共享不斷更新種群中個(gè)體的飛行方向,朝著優(yōu)化目標(biāo)的方向飛行。由于粒子群優(yōu)化算法中的粒子僅包含速度和位置信息,故需要通過對(duì)粒子本身速度和位置的不斷更新來(lái)逐漸向全局最優(yōu)解方向運(yùn)動(dòng)。粒子群優(yōu)化算法通過跟蹤解空間中個(gè)體和群體的歷史最優(yōu)解作為全局最優(yōu)解的數(shù)據(jù)集[12-13]。
根據(jù)粒子群優(yōu)化算法的基本原理,總結(jié)出算法所用到的參數(shù)如下:
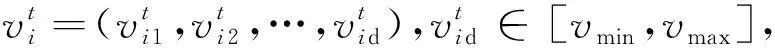
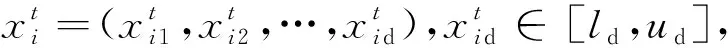
其中1≤i≤M,1≤d≤D,M為算法中種群粒子個(gè)數(shù),D為優(yōu)化目標(biāo)函數(shù)中變量維數(shù)。
粒子在t+1時(shí)刻關(guān)于速度和位置更新公式如下:
(44)
(45)
式中:r1和r2為(0,1)之間隨機(jī)數(shù);c1和c2為因子。
為了能夠更加準(zhǔn)確地控制粒子開發(fā)和探索的比重,提升粒子群優(yōu)化算法的全局尋優(yōu)能力,一些學(xué)者在原有算法基礎(chǔ)上通過在更新上增加慣性權(quán)重系數(shù),原有粒子飛行速度更新公式轉(zhuǎn)化為:
(46)
慣性權(quán)重系數(shù)ω用于調(diào)節(jié)種群中的粒子保持目前速度影響權(quán)重,根據(jù)實(shí)際經(jīng)驗(yàn)ω的取值一般選取0.12~0.90為宜[14]。為了更加直觀地了解粒子群優(yōu)化算法的流程,粒子群優(yōu)化算法流程見圖8。
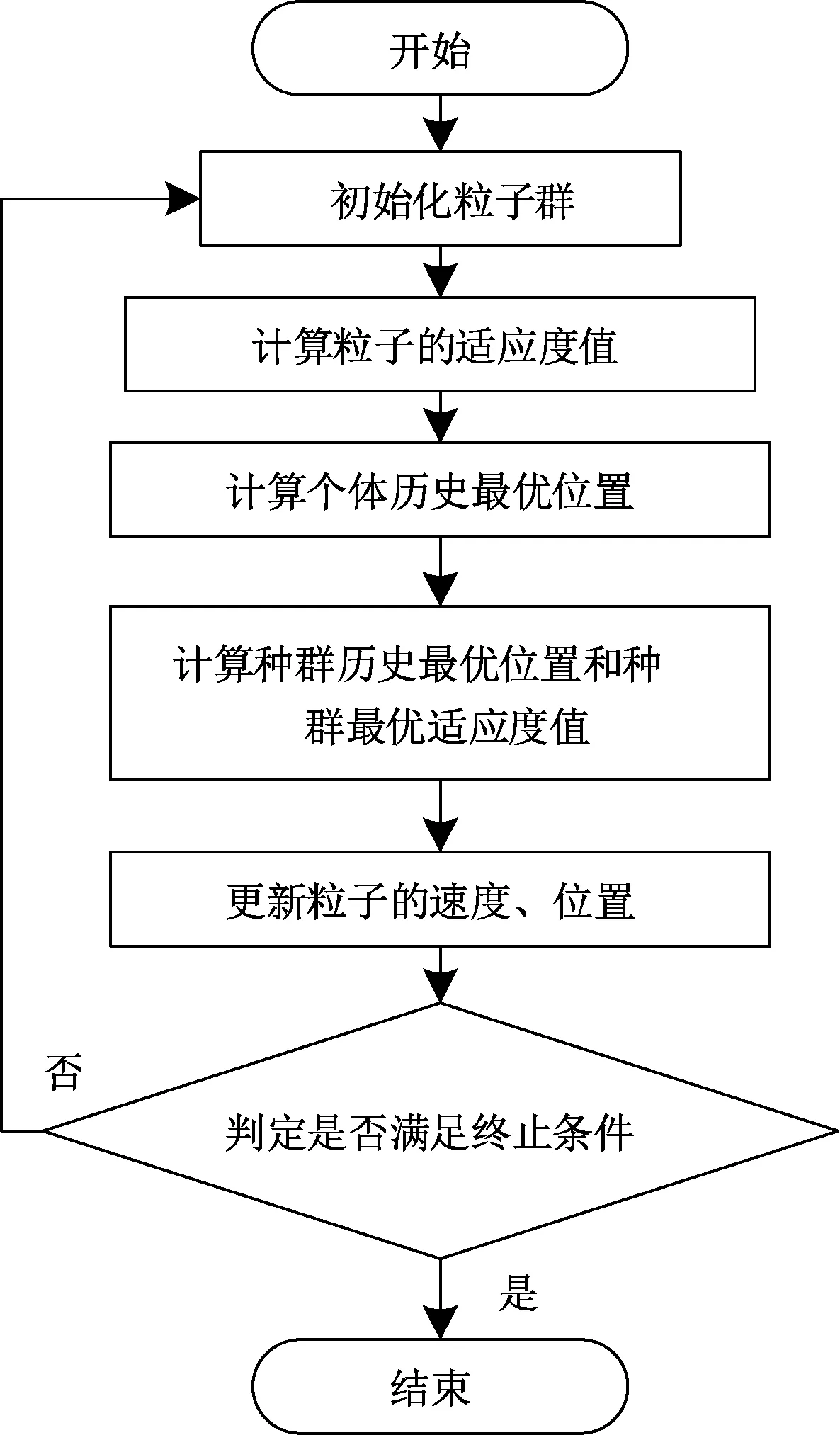
圖8 粒子群優(yōu)化算法流程
3 基于粒子群優(yōu)化算法結(jié)構(gòu)參數(shù)優(yōu)化
3.1 初始結(jié)構(gòu)參數(shù)仿真結(jié)果及分析
根據(jù)1.1中出紗口紗線速度表達(dá)式、1.2中碳纖維紗線用編織錠子中紗線長(zhǎng)度變化的計(jì)算和1.3中建立的紗線張力模型,使用MatLab軟件完成碳纖維紗線用編織錠子的紗線張力模型仿真,線墜角度變化圖和出紗口紗線張力變化圖分別如圖9、10所示。
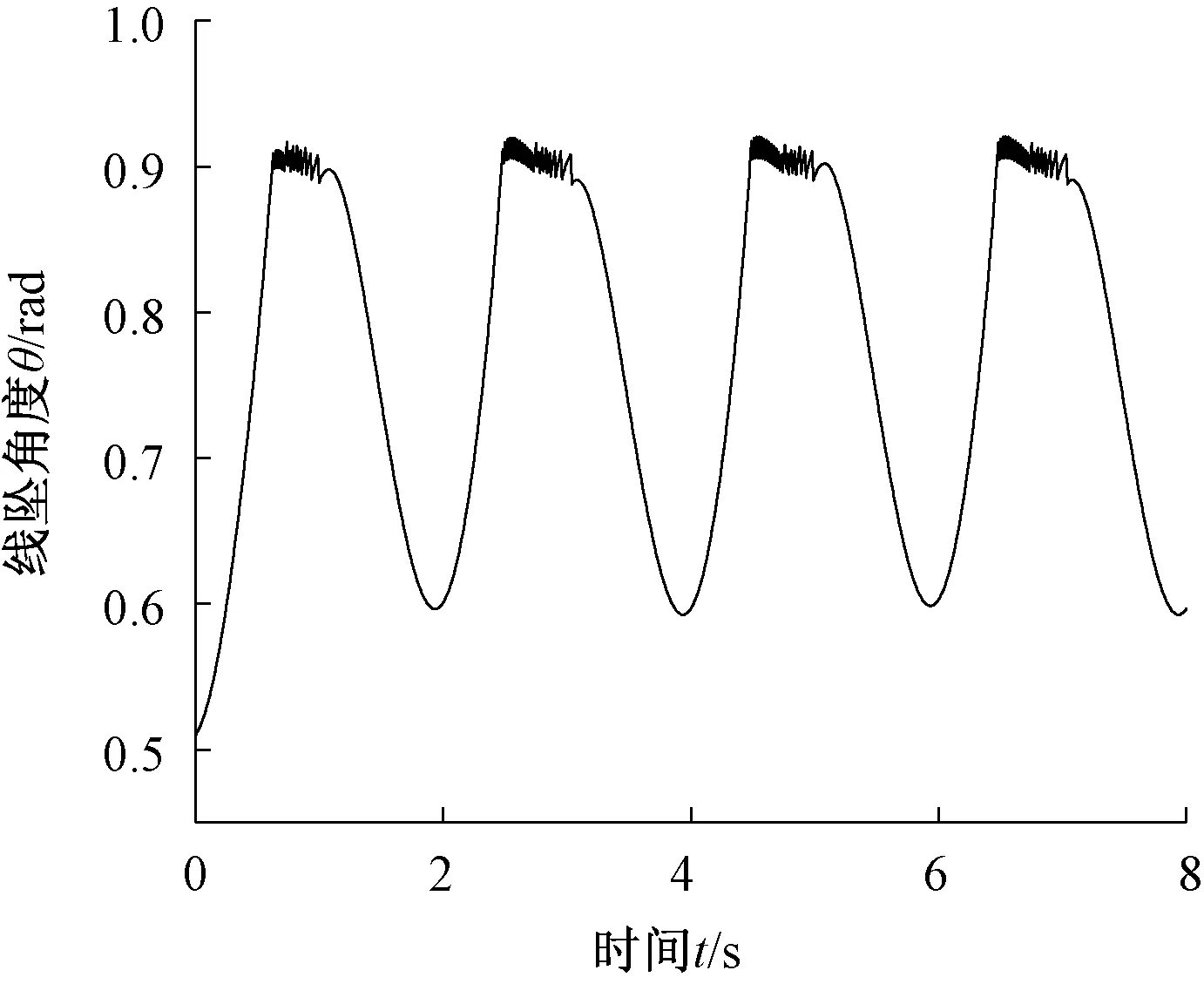
圖9 線墜角度變化圖
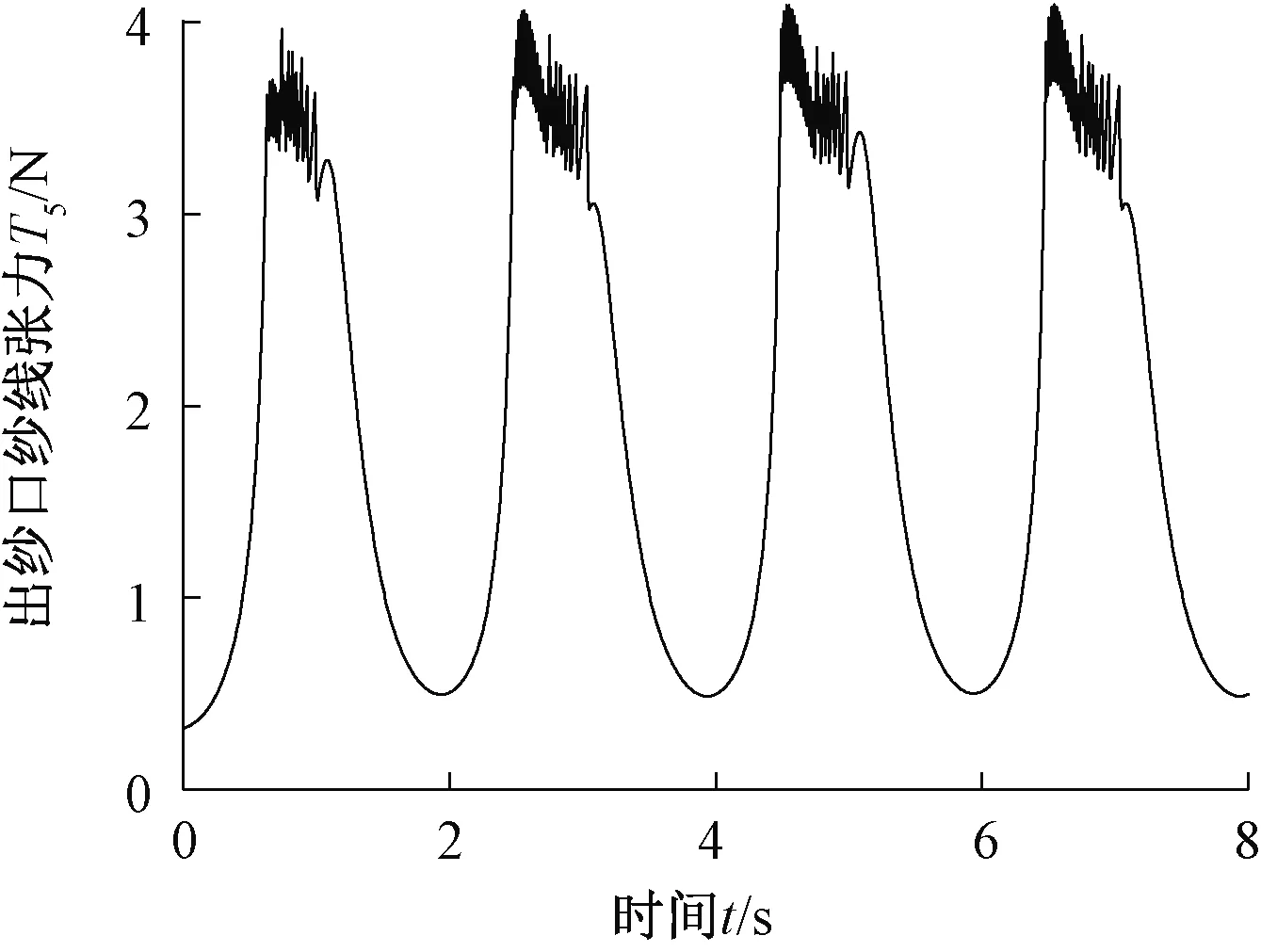
圖10 出紗口紗線張力變化圖
從圖10可以看出,編織錠子在6 s后進(jìn)入穩(wěn)定工作階段,出紗口紗線張力T5基本呈現(xiàn)周期性變化,因此詳細(xì)分析6~8 s之間的碳纖維紗線張力仿真結(jié)果。在編織過程中碳纖維紗線用編織錠子放紗階段紗線張力在3~4 N之間波動(dòng),波動(dòng)范圍較大且波動(dòng)不夠平穩(wěn)。同時(shí)在6~8 s時(shí)間范圍內(nèi),出紗口紗線張力T5會(huì)因出紗口與編織點(diǎn)之間紗線段長(zhǎng)度變化而發(fā)生大張力變化即大波動(dòng)。放紗階段碳纖維紗線處于較大紗線張力階段,由于放紗階段紗線張力的大范圍波動(dòng)會(huì)導(dǎo)致碳纖維單絲在大變應(yīng)力作用下發(fā)生斷裂,從而嚴(yán)重影響編織產(chǎn)品質(zhì)量和力學(xué)性能,因此有必要優(yōu)化碳纖維紗線用編織錠子結(jié)構(gòu)參數(shù)。同時(shí)還可以針對(duì)不同編織任務(wù)調(diào)整碳纖維紗線張力的波動(dòng)范圍,計(jì)算出合適的碳纖維紗線用編織錠子結(jié)構(gòu)參數(shù),從而提高編織產(chǎn)品合格率。
3.2 優(yōu)化目標(biāo)及優(yōu)化目標(biāo)函數(shù)
3.2.1 優(yōu)化目標(biāo)
碳纖維紗線用編織錠子通過線墜旋轉(zhuǎn)、滑輪1、2運(yùn)動(dòng)和紗線筒放紗來(lái)調(diào)節(jié)碳纖維紗線張力。但碳纖維紗線張力波動(dòng)會(huì)導(dǎo)致編織成品產(chǎn)生缺陷。為了獲得更緊湊的編織產(chǎn)品,可以通過設(shè)定碳纖維紗線用編織錠子的優(yōu)化目標(biāo),使用粒子群優(yōu)化算法優(yōu)化碳纖維紗線用編織錠子結(jié)構(gòu)參數(shù)來(lái)實(shí)現(xiàn)。優(yōu)化目標(biāo)如下:①使碳纖維紗線張力在所需值附近波動(dòng);②降低放紗階段的平均紗線張力波動(dòng);③降低編織過程中大張力變化。
3.2.2 優(yōu)化目標(biāo)函數(shù)
根據(jù)工廠實(shí)際編織情況選擇適合碳纖維紗線編織的編織張力為5 N,結(jié)合優(yōu)化目標(biāo)和碳纖維紗線用編織錠子初始結(jié)構(gòu)參數(shù)的仿真結(jié)果,選擇優(yōu)化的時(shí)間區(qū)間為6~8 s,可得優(yōu)化目標(biāo)函數(shù)的表達(dá)式如下:
(47)
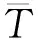
3.3 結(jié)構(gòu)參數(shù)選擇及優(yōu)化范圍確定
根據(jù)對(duì)1.2和1.3中紗線長(zhǎng)度計(jì)算和紗線張力模型分析可知,編織過程中碳纖維紗線張力主要受彈簧1、2、3的影響。彈簧1、2、3的工作時(shí)間主要由以下因素決定:θmin、θmid、θmax和l0。因此選擇以下碳纖維紗線用編織錠子結(jié)構(gòu)參數(shù)進(jìn)行優(yōu)化:彈簧1的預(yù)壓縮量Δs1、彈簧2的預(yù)壓縮量Δs2、彈簧3的預(yù)壓縮量Δs3、彈簧1的彈簧剛度k1、彈簧2的彈簧剛度k2、彈簧3的彈簧剛度k3、線墜初始角度θmin、提桿與棘爪桿接觸角度θmid、棘爪桿離開棘輪角度θmax、線墜長(zhǎng)度l0。
根據(jù)對(duì)碳纖維紗線用編織錠子初始結(jié)構(gòu)參數(shù)的仿真結(jié)果進(jìn)行分析后發(fā)現(xiàn),為了獲得最優(yōu)的編織錠子結(jié)構(gòu)參數(shù)必須擴(kuò)大和調(diào)整線墜的旋轉(zhuǎn)角度范圍。如圖3所示,θmin、θmid和θmax的取值范圍與碳纖維紗線用編織錠子的結(jié)構(gòu)有關(guān),根據(jù)碳纖維紗線用編織錠子的結(jié)構(gòu)選取的最小值θmin和最大值θmax。線墜長(zhǎng)度l0的取值范圍與碳纖維紗線用編織錠子的結(jié)構(gòu)尺寸和零部件之間的干涉有關(guān),需要根據(jù)這2個(gè)因素進(jìn)行參數(shù)范圍的選取。k1、k2、k3、Δs1、Δs2和Δs3的值需要根據(jù)碳纖維紗線用編織錠子初始結(jié)構(gòu)參數(shù)適當(dāng)增加選擇范圍,綜上所述碳纖維紗線用編織錠子初始結(jié)構(gòu)參數(shù)如表1所示,碳纖維紗線用編織錠子的結(jié)構(gòu)參數(shù)優(yōu)化范圍如表2所示。
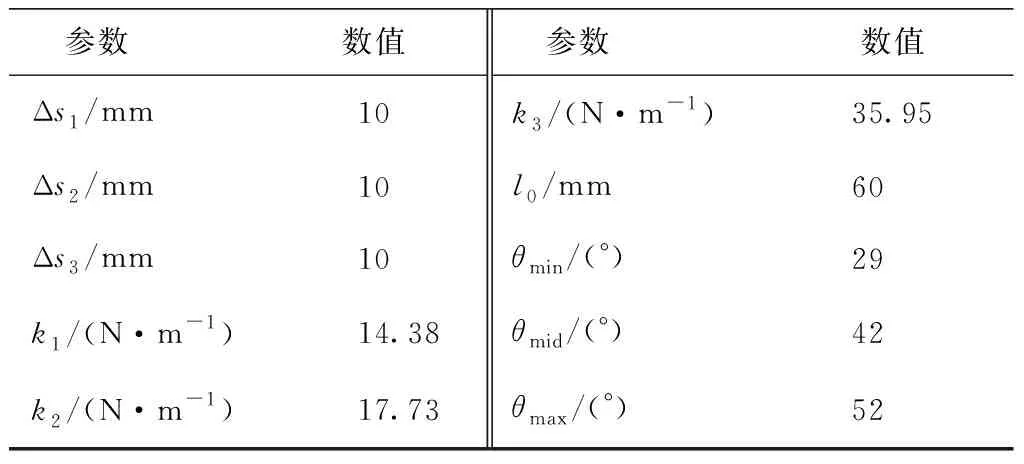
表1 碳纖維紗線用編織錠子初始結(jié)構(gòu)參數(shù)

表2 碳纖維紗線用編織錠子結(jié)構(gòu)參數(shù)優(yōu)化范圍
3.4 編織錠子結(jié)構(gòu)參數(shù)優(yōu)化結(jié)果及分析
根據(jù)優(yōu)化目標(biāo)函數(shù)和編織錠子結(jié)構(gòu)參數(shù)優(yōu)化范圍,完成粒子群優(yōu)化算法中參數(shù)設(shè)置,粒子群優(yōu)化算法優(yōu)化前后出紗口紗線張力變化圖見圖11。
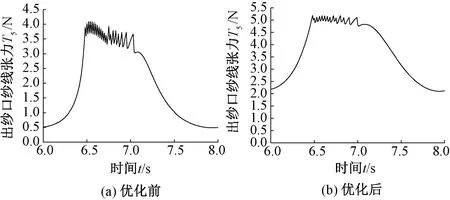
圖11 粒子群優(yōu)化算法優(yōu)化前后出紗口紗線張力變化圖
圖11(a)所示為碳纖維紗線用編織錠子初始結(jié)構(gòu)參數(shù)條件下在6~8 s時(shí)間范圍內(nèi)出紗口紗線張力T5隨時(shí)間變化的曲線圖,可以看出,在放紗階段出紗口處紗線張力約在3.5 N附近波動(dòng),且波動(dòng)幅度范圍變化較大,波動(dòng)不夠平穩(wěn),不利于碳纖維紗線的編織。如圖11(b)所示,為使用粒子群優(yōu)化算法優(yōu)化后的出紗口紗線張力T5隨時(shí)間變化的曲線圖,在放紗階段出紗口紗線張力在5 N附近波動(dòng),相比于優(yōu)化前放紗階段紗線張力波動(dòng)更加平穩(wěn),且波動(dòng)范圍變化不大,符合優(yōu)化目標(biāo)。粒子群優(yōu)化算法優(yōu)化前后的紗線張力比較如表3所示。
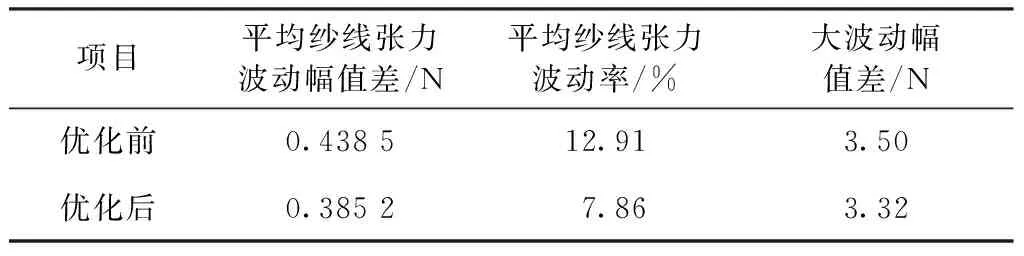
表3 粒子群優(yōu)化算法優(yōu)化前后的紗線張力比較
由表3可知,編織錠子結(jié)構(gòu)參數(shù)優(yōu)化后放紗階段平均紗線張力波動(dòng)率相比于優(yōu)化前下降了5.05%,大波動(dòng)幅值差相比于優(yōu)化前下降了0.18 N。證明使用粒子群優(yōu)化算法優(yōu)化編織錠子結(jié)構(gòu)參數(shù)對(duì)于降低紗線張力波動(dòng)是有效果的。粒子群優(yōu)化算法優(yōu)化前后結(jié)構(gòu)參數(shù)如表4所示。
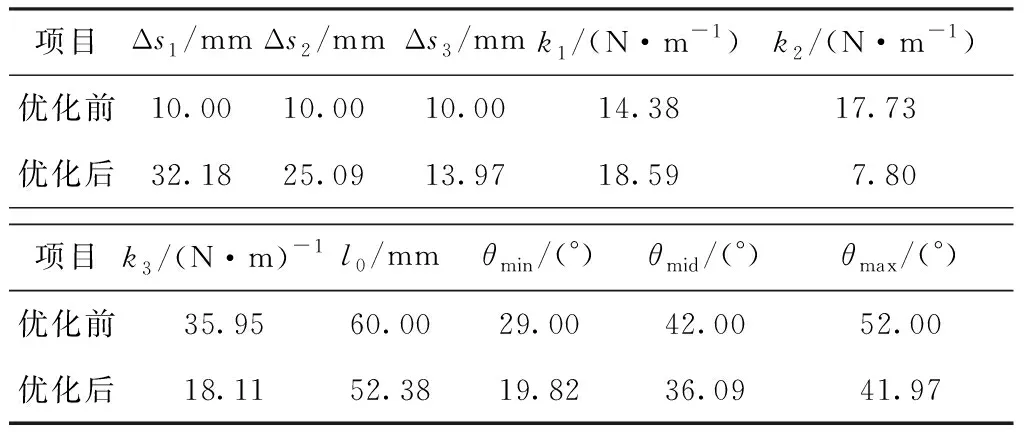
表4 粒子群優(yōu)化算法優(yōu)化前后結(jié)構(gòu)參數(shù)
為了驗(yàn)證碳纖維紗線用編織錠子結(jié)構(gòu)參數(shù)優(yōu)化后結(jié)果更適合碳纖維紗線編織,需要與其他類型編織錠子實(shí)驗(yàn)結(jié)果進(jìn)行比較。文獻(xiàn)[15]中通過電壓傳感器測(cè)量編織機(jī)編織過程中單補(bǔ)償編織錠子實(shí)時(shí)紗線張力,根據(jù)文獻(xiàn)[15]中單補(bǔ)償編織錠子紗線張力實(shí)測(cè)數(shù)據(jù)和圖11中數(shù)據(jù)分析可知,碳纖維紗線用編織錠子放紗階段平均紗線張力波動(dòng)率相比于單補(bǔ)償編織錠子下降了18.13%,證明碳纖維紗線用編織錠子放紗階段平均紗線張力波動(dòng)更小,更適合碳纖維紗線的編織。
4 結(jié) 論
本文以自主設(shè)計(jì)的碳纖維紗線用編織錠子為基礎(chǔ),結(jié)合花柱編織工藝和編織錠子中紗線長(zhǎng)度計(jì)算表達(dá)式,分階段建立了碳纖維紗線用編織錠子紗線張力模型,得到了結(jié)構(gòu)參數(shù)與碳纖維紗線張力之間的關(guān)系。然后通過MatLab軟件使用粒子群優(yōu)化算法完成碳纖維紗線用編織錠子的結(jié)構(gòu)參數(shù)優(yōu)化,并對(duì)優(yōu)化結(jié)果進(jìn)行比較和分析,得出如下結(jié)論:
①通過分析碳纖維紗線用編織錠子中紗線長(zhǎng)度變化,結(jié)合碳纖維紗線用編織錠子中各構(gòu)件受力分析,建立的紗線張力模型,所得仿真結(jié)果能夠更加直觀地看出編織過程中紗線張力的變化過程。
②通過調(diào)節(jié)彈簧剛度、彈簧預(yù)載荷長(zhǎng)度、線墜擺動(dòng)角度和線墜長(zhǎng)度可以使放紗階段紗線張力保持在所需值附近較小范圍內(nèi)波動(dòng)。
③使用粒子群優(yōu)化算法優(yōu)化碳纖維紗線用編織錠子結(jié)構(gòu)參數(shù)后,放紗階段平均紗線張力波動(dòng)率相比于優(yōu)化前有明顯下降,相比于單補(bǔ)償編織錠子實(shí)驗(yàn)數(shù)據(jù)下降了18.13%,證明使用粒子群優(yōu)化算法優(yōu)化編織錠子結(jié)構(gòu)參數(shù)是有效果且具備可行性的。

