變截面梁單元在任意荷載作用下固端內力的統一計算方法
趙志強,丁婷,丁圣果,李綺文
(1.貴陽市建筑設計院有限公司,貴陽550003;2.貴州大學土木工程學院,貴陽550003;3.貴州大學明德學院,貴陽550003)
1 引言
在桿系有限元編程中,總荷載列陣由各單元的固端力列陣集成:
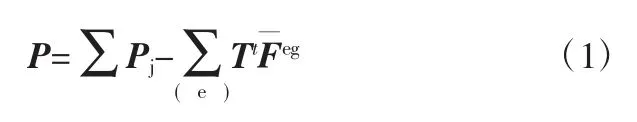
式中,為局部坐標系下的固端力列陣;Tt為坐標轉換陣;Pj為結點荷載列陣。
的計算一般均按結構力學固端彎矩表中的計算式,并根據荷載形式用選擇轉向語句完成計算,對于桿截面變化的單元或較復雜的荷載形式,則存在計算程序的前處理輸入冗繁,若采用實體單元,計算結果為應力,需作剖面將應力再轉換成該剖面內力。采用基于力法的奇異函數方法及高斯求積法,有效解決了這一難題,編程方便簡捷。
2 變截面桿固端內力列陣的統一計算式
2.1 計算固端內力的力法方程
任意變截面桿單元在任意荷載作用下的固端內力計算可用力法導出[1],僅以連續梁單元為例,單元ij(見圖1a)在豎向荷載作用下,計算固端彎矩的基本結構為端部鉸支的靜定梁,如圖1b 所示。

圖1 漸變截面桿元及其基本結構
力法典型方程為:

式中,δij為柔度系數;Xi為x方向的力;ΔiP為荷載系數。
方程中的柔度系數δij(i=1,2;j=1,2)計算式為:

I(x)為桿截面慣性矩:

方程中的自由項:

式(3)和式(6)被積函數是x的分式,很難用一般積分運算完成。可采用高斯求積法進行積分運算。
(1)基坑的周圍具有一個邊界效應,即在基坑外的濕陷量量會迅速的減小,而基坑內部中心點沉降量最大,其沉降量沿半徑方向較為均勻的減小。
2.2 用奇異函數表達的任意荷載作用下基本結構彎矩MP(x)統一公式
基本結構在任意荷載作用下的彎矩MP(x)可采用截面法導出,用奇異函數統一表達為:

該函數在編程中采用條件賦值語句即可實現。
V0為簡支梁右端支反力(見圖2);對于每一個集中力Pk(k=1,…,np),幾何參數akp為集中力所在位置;對于每一段分布力qk,Δqk(k=1,…,nq),幾何參數bskq,bekq分別為分布力的起始位置和終止位置;式(6)已能既括梁上常見的大部分荷載工況(見圖2),當作用均布荷載時,取Δqk=0;當作用有梯形分布荷載時,取q0k>0,Δqk>0 或q0k>0,Δqk<0;三角形分布荷載是梯形分布荷載的特殊情況,取q0k=0,Δqk>0 或q0k>0,Δqk=-q0k。
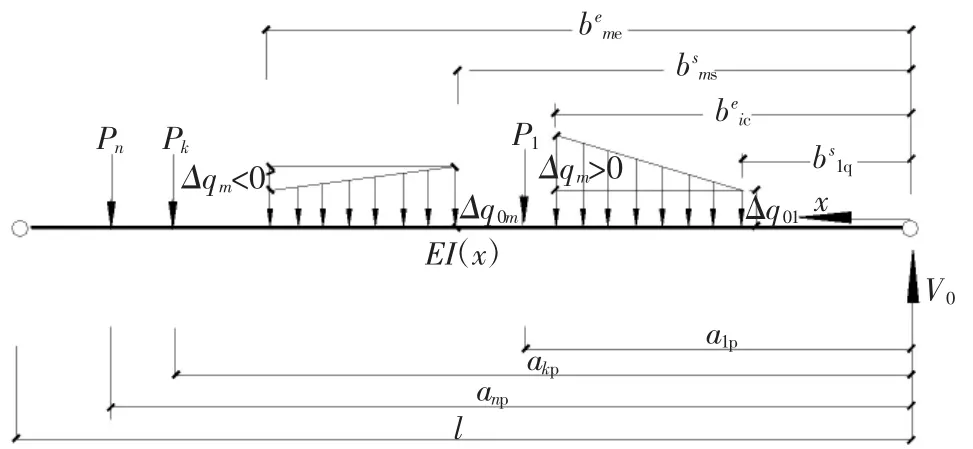
圖2 任意荷載作用下的基本結構
2.3 梁變截面高 的表達形式
當梁截面高連續變化時,h(x)是x的連續函數,例如,梯形變截面高的梁(見圖3a)
由截面尺寸的幾何函數可確定矩形截面梁的截面慣性矩(Ix),如矩形截面


圖3 變截面梁
2.4 計算固端彎矩的高斯求積法


式中,ζi為非等距積分點值,是勒讓德多項式方程的根,Hi為權值,nζ為積分點數,其值如表1 所示。

表1 高斯積分點及權值
原則上積分域范圍[-1,1]的積分點數nζ可取2,3,…,式(3)和式(6)的積分采用高斯求積法完成而不至造成較大誤差的條件是被積函數F(ζ)不存在間斷點,經大量算例計算結果分析對比,對積分點數nζ的取值可按如下原則確定:
1)當MP(x)在(0≤x≤1)為連續函數且梁截面高h(x)也連續時,如分布荷載作用下的漸變截面梁,取nζ=3 已能很好地滿足計算結果的精度要求;
2)當MP(x)的一階導數不連續時,如集中力作用的MP(x)圖,插值點數宜選多些,在后面算例中均取nζ=7;
3)當MP(x)存在第一類間斷點,如梁結間作用有集中力矩時的MP(x)或梁截面分段突變,h(x)存在第一類間斷點時,宜將集中力作用點及截面尺寸突變點設為單元結點。
用式(9)完成式(3)和式(6)的定積分運算后,桿的固端彎矩(方程(2)的解)為:

式中,V0ij,V0ji分別為簡支梁左、右端剪力。
3 算例
表2 中各算例給出的計算結果精度在大量計算中具有典型性,表明采用本文方法計算的固端內力誤差小于1%。
4 結論及討論
1)采用基于力法的高斯求積運算計算桿單元的固端內力,計算結果精度可達99%以上。
2)方法適用于任意結間荷載作用下的梁單元固端內力計算,編程無須逐一根據荷載形式按結構力學固端內力公式計算。事實上,任何結構力學書籍中也不可能將各種荷載分布形式的固端內力計算概括完全。
3)方法適用于任意漸變截面梁單元,這是在現有桿系有限元程序中是難于實現的,當梁截面變化時,常規有限元程序只能用把梁域細分為較多高階實體單元,其計算結果以細小單元應力形式給出,對桿系結構的工程應用中,需截面內力的計算結果并不方便。
4)在形成有限元法荷載列陣的編程中,采用本文的計算模型及方法,編程方便,計算力法方程中的柔度系數δij及自由項ΔiP僅需單層幾次循環,循環數次根據高斯插值點數決定。
5)本文的方法也宜用于漸變截面單元的局部坐標系單剛推導[4]。因此,完成漸變截面桿系結構在任意荷載作用下的有限元編程完全可行,在這方面做的大量工作表明計算結果精確。
6)當梁域結間存在集中力矩或梁截面分段突變時,由于被積函數存在第一類間斷點,將整段梁作為一個單元計算時高斯積分法可能造成較大誤差,這種情況可在集力力矩作用點及截面尺寸突變點劃分單元結點。

表2 固端內力計算值

