集合與函數核心考點綜合演練
劉中亮
一、選擇題
1.已知集合A={x|x-1≥0},B={0,1,2},則A∩B=( )。
A.{0} B.{1}
C.{1,2} D.{0,1,2}
2.已知集合A={x|x2-x-2>0},則?RA=( )。
A.{x|-1<x<2}
B.{x|-1≤x≤2}
C.{x|x<-1}∪{x|x>2}
D.{x|x≤-1}∪{x|x≥2}
3.設全集U=R,集合A={x|x≥3},B={x|0≤x<5},則(?UA)∩B=( )。
A.{x|0<x<3} B.{x|0≤x≤3}
C.{x|0<x≤3} D.{x|0≤x<3}
4.已知集合A={1,2,3},B={x|x2-3x+a=0,a∈A},若A∩B≠?,則a的值為( )。
A.1 B.2
C.3 D.1或2
5.設全集U=R,集合A={x|x2-2x-3<0},B={x|x-1≥0},則圖1中陰影部分所表示的集合為( )。
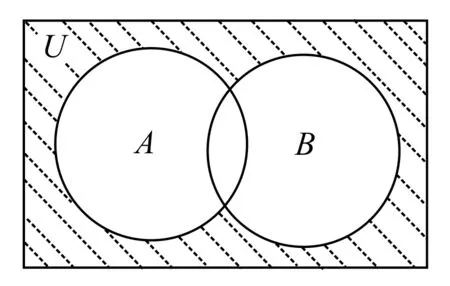
圖1
A.{x|x≤-1或x≥3}
B.{x|x<1或x≥3}
C.{x|x≤1}
D.{x|x≤-1}
6.某班共40 人,其中24 人喜歡籃球運動,16人喜歡乒乓球運動,6人這兩項運動都不喜歡,則喜歡籃球運動但不喜歡乒乓球運動的人數為( )。
A.17 B.18
C.19 D.20
7.已知集合A={0},B={-1,0,1},若A?C?B,則符合條件的集合C的個數為( )。
A.1 B.2
C.4 D.8
8.已知集合A={1,2,3,4,5,6},B={3,4,5,X},若B?A,則X可 以 取 的 值為( )。
A.1,2,3,4,5,6 B.1,2,3,4,6
C.1,2,3,6 D.1,2,6
9.已知a為給定的實數,那么集合M={x|x2-3x-a2+2=0,x∈R}的子集的個數為( )。
A.1 B.2
C.4 D.不確定

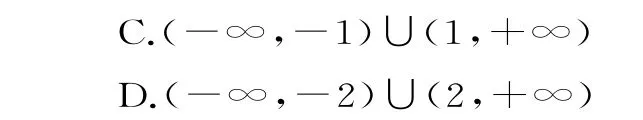
13.已知函數f(x)=x2-2x-3,則該函數的單調遞增區間為( )。
A.(-∞,1] B.[3,+∞)C.(-∞,-1] D.[1,+∞)
14.設f(x)-x2=g(x),x∈R,若函數f(x)為偶函數,則g(x)的解析式可以為( )。
A.g(x)=x3B.g(x)=cosx
C.g(x)=1+xD.g(x)=xex
16.已知函數f(x)為奇函數,當x>0時,f(x)單調遞增,且f(1)=0,若f(x-1)>0,則x的取值范圍為( )。
A.{x|0<x<1或x>2}
B.{x|x<0或x>2}
C.{x|x<0或x>3}
D.{x|x<-1或x>1}
17.已知f(x)在R 上是奇函數,且滿足f(x+4)=f(x),當x∈(0,2)時,f(x)=2x2,則f(7)=( )。
A.-2 B.2
C.-98 D.98
18.定義在R 上的偶函數f(x)滿足f(x)=f(x+2),且在[-1,0]上單調遞減,設a=f(2),b=f(2),c=f(3),則a,b,c的大小關系是( )。
A.b<c<aB.a<b<c
C.b<a<cD.a<c<b
(2)小組在分組進行討論時,教師不是放手讓學生去漫無邊際地討論,而是要發揮好“領路人”的作用,這是中職學生的自我學習能力和自覺性局限性所致。當學生討論的思路偏離或者遇到障礙時,教師要及時提供幫助。


20.已知f(x)是定義在R 上的奇函數,且當x>0 時,f(x)=x2-x,則 不 等 式f(x)>0的解集用區間表示為( )。
A.(-1,1)
B.(-∞,-1)∪(1,+∞)
C.(-∞,-1)∪(0,1)
D.(-1,0)∪(1,+∞)
21.若 函 數f(x)=2|x-a|+3 在 區 間[1,+∞)上不單調,則實數a的取值范圍是( )。
A.[1,+∞) B.(1,+∞)
C.(-∞,1) D.(-∞,1]
22.已知函數f(x)在[0,4]上是增函數,且函數y=f(x+4)是偶函數,則下列結論正確的是( )。
B.f(2)<f(5)<f(4)
C.f(5)<f(4)<f(2)
D.f(4)<f(2)<f(5)
23.已知奇函數f(x)的定義域為R,當x∈(0,2]時,f(x)=x2+1,且函數f(x+1)為偶函數,則f(2018)+f(-2019)的值為( )。
A.7 B.2
C.-7 D.3
24.已知f(x)是定義域為(-1,1)的奇函數,而且f(x)是減函數,如果f(m-2)+f(2m-3)>0,那么實數m的取值范圍是( )。
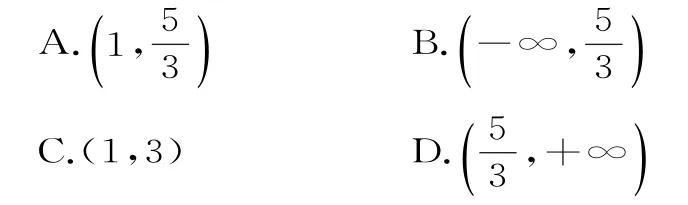
二、填空題
25.已知全集U=R,集合A={x|x<3或x≥7},B={x|x<a}。若(?UA)∩B≠?,則實數a的取值范圍為____。
26.設集合A={x|x+m≥0},B={x|-2<x<4},全集U=R,且(?UA)∩B=?,則實數m的取值范圍為____。
27.對于任意兩個集合A,B,定義AB={x|x∈A且x?B},A*B=(A-B)∪(B-A),記A={y|y≥0},B={x|-3≤x≤3},則A*B=____。

三、解答題
35.若集合A={(x,y)|x2+mx-y+2=0,x∈R},B={(x,y)|x-y+1=0,0≤x≤2},當A∩B≠?時,求實數m的取值范圍。
36.已知集合A={x|x2-3x+2=0},B={x|x2+2(a+1)x+a2-5=0}。
(1)若A∩B={2},求實數a的值。
(2)若A∪B=A,求實數a的取值范圍。
37.已知集合A={x|x<-2或x>3},B={x|4x+m<0},當A?B時,求實數m的取值范圍。
38.設f(x)是(-∞,+∞)上的奇函數,f(x+2)=-f(x),當0≤x≤1 時,函數f(x)=x。
(1)求f(π)的值。
(2)當-4≤x≤4 時,求f(x)的圖像與x軸所圍成圖形的面積。
39.已知函數y=f(x)在定義域[-1,1]上既是奇函數,又是減函數。
(1)求證:對任意x1,x2∈[-1,1],都有[f(x1)+f(x2)](x1+x2)≤0。
(2)若f(1-a)+f(1-a2)<0,求實數a的取值范圍。
40.設f(x)是定義域為(-∞,0)∪(0,+∞)的奇函數且在(-∞,0)上為增函數。
(1)若m·n<0,m+n≤0,求 證:f(m)+f(n)≤0。
(2)若f(1)=0,解關于x的不等式f(x2-2x-2)>0。

一、選擇題
1.提示:由A={x|x-1≥0}={x|x≥1},B={0,1,2},可得A∩B={1,2}。應選C。
2.提示:由x2-x-2>0,可得(x-2)·(x+1)>0,解得x>2或x<-1,所以A={x|x>2 或x<-1},則?RA={x|-1≤x≤2}。應選B。
3.提示:由題意可得,?UA={x|x<3},所以(?UA)∩B={x|0≤x<3}。應選D。
4.提示:當a=1時,x2-3x+1=0,無整數解,則A∩B=?;當a=2時,B={1,2},A∩B={1,2}≠?;當a=3時,B=?,A∩B=?。因此實數a=2。應選B。
5.提示:圖中陰影部分表示的集合為?U(A∪B)。由A={x|-1<x<3},B={x|x≥1},可得A∪B={x|x>-1},所以?U(A∪B)={x|x≤-1}。應選D。
6.提示:記全集U為該班全體同學,喜歡籃球運動的記作集合A,喜歡乒乓球運動的記作集合B,則喜歡籃球但不喜歡乒乓球運動的記作A∩?UB(圖略)。易得人數為18。應選B。
7.提示:由題意可得,含有元素0且是集合B的子集的集合有{0},{0,-1},{0,1},{0,-1,1},即符合條件的集合C共有4個。應選C。
8.提示:由B?A和集合元素的互異性可知,X可以取的值為1,2,6。應選D。
9.提示:由方程x2-3x-a2+2=0,可得Δ=1+4a2>0,所以方程有兩個不相等的實根,所以集合M有2個元素,所以集合M有22=4(個)子集。應選C。


12.提 示:當a≥0 時,不 等 式 可 化 為a(a2+a-3a)>0,即a2+a-3a>0,即a2-2a>0,解得a>2 或a<0(舍去);當a<0時,不等式可化為a(-3a-a2+a)>0,即-3a-a2+a<0,即a2+2a>0,解得a<-2或a>0(舍去)。綜上可知,實數a的取值范圍為(-∞,-2)∪(2,+∞)。應選D。
13.提示:設t=x2-2x-3。由t≥0,可得x2-2x-3≥0,解得x≤-1或x≥3,所以函數f(x)的定義域為(-∞,-1]∪[3,+∞)。因為函數t=x2-2x-3的圖像的對稱軸為x=1,所以函數t在(-∞,-1]上單調遞減,在[3,+∞)上單調遞增。故函數f(x)的單調遞增區間為[3,+∞)。應選B。
14.提示:因為f(x)=x2+g(x),且函數f(x)為偶函數,所以(-x)2+g(-x)=x2+g(x),即g(-x)=g(x),所以g(x)為偶函數。由選項可知,只有B 中的函數為偶函數。應選B。
15.提示:函數f(x)的定義域為[-3,0)∪(0,3],且f(-x)=-f(x),可得f(x)是奇函數,故圖像關于原點對稱。應選B。
16.提示:函數f(x)是奇函數,當x>0時,f(x)單調遞增,f(1)=0。由f(x-1)>0,可得-1<x-1<0或x-1>1,所以0<x<1或x>2。應選A。
17.提示:由f(x+4)=f(x),可得f(7)=f(3)=f(-1)。由f(x)為奇函數,可得f(-1)=-f(1),f(1)=2×12=2。故f(7)=-2。應選A。

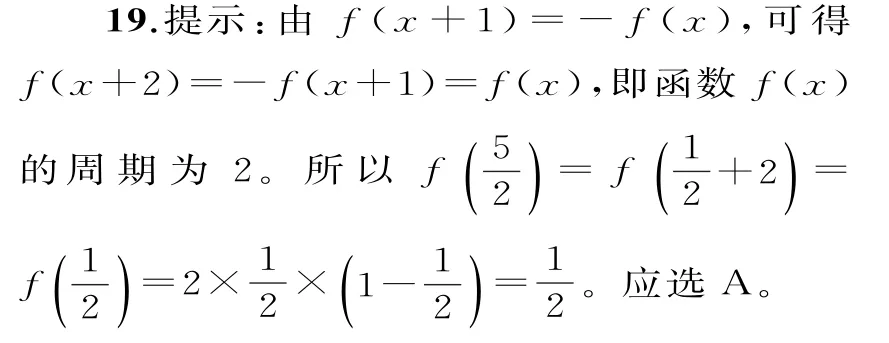
20.提示:由f(x)是定義在R 上的奇函數,可得f(0)=0。設x<0,則-x>0。當x>0時,f(x)=x2-x,可得f(-x)=x2+x。又f(-x)=-f(x),所以f(x)=-x2-x,x<0。當x>0時,由f(x)>0得x2-x>0,解得x>1 或x<0(舍去),此時x>1。當x=0時,f(0)>0不成立。當x<0時,由f(x)>0得-x2-x>0,解得-1<x<0。綜上可得,x∈(-1,0)∪(1,+∞)。應選D。
21.提示:易知函數f(x)=2|x-a|+3的增區間為[a,+∞),減區間為(-∞,a]。因為函數f(x)=2|x-a|+3 在區間[1,+∞)上不單調,所以a>1。應選B。
22.提示:因為y=f(x+4)是偶函數,所以y=f(x+4)的圖像關于直線x=0對稱,所以函數y=f(x)的圖像關于直線x=4對稱,所以f(5)=f(3)。又函數y=f(x)在[0,4]上是增函數,所以f(2)<f(3)<f(4),即f(2)<f(5)<f(4)。應選B。
23.提示:由f(x)為R 上的奇函數,f(x+1)為偶函數,可得f(x)=f(x-1+1)=f(1-x+1)=f(-x+2)=-f(x-2)=f(x-4),可知f(x)是周期為4的周期函數。故f(2018)+f(-2019)=f(2)+f(1)=5+2=7。應選A。

二、填空題
25.提示:因為A={x|x<3 或x≥7},所以?UA={x|3≤x<7}。又(?UA)∩B≠?,則a>3。答案為(3,+∞)。
26.提示:由已知A={x|x≥-m},可得?UA={x|x<-m}。由B={x|-2<x<4},(?UA)∩B=?,可得-m≤-2,即m≥2。故實數m的取值范圍為{m|m≥2}。
27.提示:由題意可知A-B={x|x>3},B-A={x|-3≤x<0},所以A*B=[-3,0)∪(3,+∞)。


30.提示:由f(x)=2x-x2,x∈(-2,2],可知f(-1)=-3,f(0)=0,f(2)=0。又f(x)的周期為4,所以f(2018)+f(2019)+f(2020)=f(2)+f(-1)+f(0)=0-3+0=-3。
31.提示:由f(x)是R 上的奇函數,可得f(0)=0。又對任意x∈R 都有f(x+6)=f(x)+f(3),可得當x=-3時,有f(3)=f(-3)+f(3)=0,可得f(-3)=0,f(3)=0,可得f(x+6)=f(x),可知其周期為6。故f(2019)=f(3)=0。
32.提示:因為f(x)的圖像關于直線x=2對稱,所以f(x)=f(4-x),f(-x)=f(4+x)。又f(-x)=f(x),所以f(x)=f(4+x),可知其周期為4,則f(-1)=f(4-1)=f(3)=3。

三、解答題

故m的取值范圍為(-∞,-1]。
36.提示:(1)由A={x|x2-3x+2=0}={1,2},A∩B={2},可得2∈B,2 是方程x2+2(a+1)x+a2-5=0 的根,所以a2+4a+3=0,即a=-1或a=-3。經檢驗a的取值符合題意,故a=-1或a=-3。
(2)由A∪B=A,可得B?A。
當B=?時,由Δ=4(a+1)2-4(a2-5)<0,解得a<-3。
當B只有一個元素時,Δ=0,即a=-3。同理當B有兩個元素時,a>-3。當B≠? 時,由B={1},利用韋達理可知a∈?;由B={2},利用韋達定理可解得a=-3;由B={1,2},利用韋達定理可知a∈?。
綜上可知,a的取值范圍是(-∞,-3]。

38.提示:(1)由f(x+2)=-f(x),可得f(x+4)=f[(x+2)+2]=-f(x+2)=f(x),所以f(x)是以4 為周期的周期函數,所以f(π)=f(π-4)=-f(4-π)=-(4-π)=π-4。
(2)由f(x)是奇函數且f(x+2)=-f(x),可得f[(x-1)+2]=-f(x-1)=f[-(x-1)],即f(1+x)=f(1-x),故函數y=f(x)的圖像關于直線x=1對稱。
又當0≤x≤1時,f(x)=x,且f(x)的圖像關于原點成中心對稱,據此畫出f(x)的大致圖像,如圖2所示。
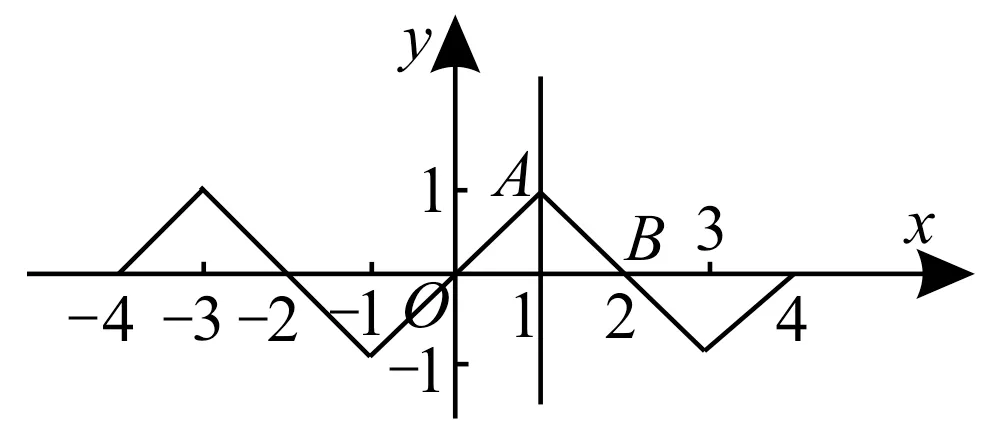
圖2
設當-4≤x≤4時,f(x)的圖像與x軸圍成的圖形面積為S,則S=4S△OAB=4。
39.提示:(1)若x1+x2=0,顯然原不等式成立。
若x1+x2<0,則-1≤x1<-x2≤1。因為f(x)在[-1,1]上是減函數且為奇函數,所以f(x1)>f(-x2)=-f(x2),所以f(x1)+f(x2)>0。所以[f(x1)+f(x2)]·(x1+x2)<0成立。
若x1+x2>0,則-1≤-x2<x1≤1。同理可證f(x1)+f(x2)<0,所以[f(x1)+f(x2)](x1+x2)<0成立。
綜上所述,對任意x1,x2∈[-1,1],都有[f(x1)+f(x2)](x1+x2)≤0恒成立。
(2)f(1-a)+f(1-a2)<0?f(1-a2)<-f(1-a)=f(a-1)。
由f(x)在定義域[-1,1]上是減函數,
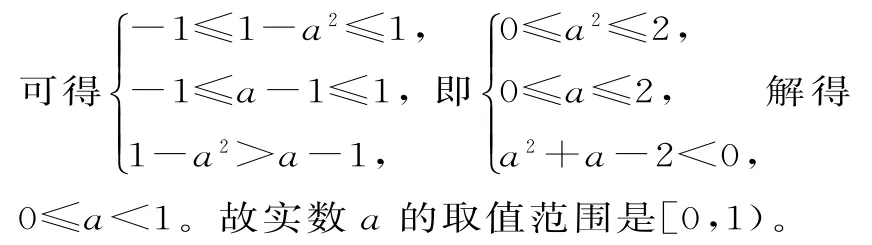
40.提示:(1)因為m·n<0,m+n≤0,所以m,n為一正一負。不妨設m>0,n<0,則n≤-m<0。取n=-m<0,由f(x)在(-∞,0)上為增函數,可得f(n)=f(-m)。取n<-m<0,同理f(n)<f(-m),所以f(n)≤f(-m)。又因為f(x)在(-∞,0)∪(0,+∞)上為奇函數,所以f(-m)=-f(m),所以f(n)+f(m)≤0。


