多個列車輪載作用下鐵路道床結構安定性分析

王康宇，莊妍，張占榮，張升

(1.浙江工業大學土木工程學院，浙江杭州，310014；2.東南大學土木工程學院混凝土及預應力混凝土結構教育部重點實驗室，江蘇南京，211189；3.長沙理工大學公路養護技術國家工程實驗室，湖南長沙，410114；4.中鐵第四勘察設計院集團有限公司，湖北武漢，430063；5.中南大學土木工程學院高速鐵路建造技術國家工程實驗室，湖南長沙，410075)

隨著工業技術和工程建設的快速發展，現代的結構設計理念需要在保證結構安全的前提下，盡可能考慮經濟效益，這就對工程設計和既有工程結構的承載性能評估提出新挑戰。鐵路和道路結構的路面、路基及其以下一定范圍內的地基在交通荷載的長期循環作用下將會產生振動，且隨著交通荷載作用次數增加而出現較大的塑性變形累積現象，其破壞形式往往是由于塑性變形逐漸累積而非突然的崩塌破壞[1]。因此，現有的基于彈性理論和經驗方法的設計與分析理念不能反映其破壞的本質。安定分析能夠有效確定交通荷載作用下結構的長期響應，反映結構破壞的本質及實際的安全程度，因而在交通荷載作用下的結構中得到了廣泛應用。SHARP等[2]將路面結構的破壞形式與安定理論建立了聯系，基于MELAN定理提出了二次曲線法(也稱圓錐曲線法)求解平面情況下單層路面和雙層路面的安定荷載，并總結了各結構層的材料參數對安定荷載的影響規律；YU 等[3]提出了基于Hertz接觸荷載的二維和三維路面結構靜力安定荷載的解析方法，但該方法放松了對殘余應力場滿足屈服條件的限制[4-5]；孫陽等[6]基于靜力安定定理研究了平面應變條件下2層路面結構的安定性，分析了路面材料參數和各結構層厚度等因素對安定荷載的影響規律；王娟等[7]總結了安定理論在道路結構中的應用情況，提出了基于安定下限定理的道路路面結構設計方法。最近，在經典靜力安定理論的基礎上，QIAN 等[8-10]基于有限元模型研究了移動荷載作用下結構中的動應力分布，通過構建穩態動應力條件下結構中的殘余應力場，提出了動力安定性下限值的預測方法，揭示了交通荷載形式和移動速度等對結構安定性的影響規律。目前，安定理論在鐵路工程中的應用多集中于輪軌接觸應力和輪軌磨損等問題，如LANGUEH等[11]考慮車輪材料的循環硬化效應，基于彈性安定和塑性安定概念，提出了基于穩態算法的數值方法，預測實際情況下車輪滾動接觸疲勞裂紋的萌生；PANUNZIO 等[12]基于彈性安定理論，假設列車輪軌服從Dang Van 準則，研究了軌道幾何不平順對輪軌動力相互作用和鋼軌疲勞磨損的影響；HASAN[13]基于von-Mises 屈服準則和Hertz 接觸理論，從輪載和鋼軌的抗拉強度出發，確定了理想的最小接觸面積，優化了輪軌型線；CHEN等[14]在計算輪軌非赫茲接觸特性和輪軌輪廓演化的基礎上，基于安定理論評估了道岔累積表面啟動滾動接觸疲勞(RCF)。同時，現有研究僅考慮了單個列車輪載作用，忽略了多輪載通過軌道結構傳遞的應力疊加作用，不能準確計算鐵路道床結構的應力分布規律[15-16]。為了更全面地了解鐵路道床的安定行為，本文基于列車輪載的傳遞機理，采用Gauss 函數計算軌枕荷載分擔比，結合Melan靜力型安定定理，研究多輪載作用下單層道床結構的安定荷載及其影響因素，以期為鐵路道床結構的優化設計提供借鑒和參考。

1 列車輪載的簡化

1.1 單個列車輪載作用的軌枕荷載分擔比

列車荷載作用于軌道結構上，經過鋼軌、軌枕和道床，最終傳遞到路基結構中。從道床-路基結構承載能力和沉降控制的角度來講，明確列車荷載的分布規律和軌枕荷載分擔比對道床-路基結構中的動應力研究和結構的優化設計具有重要的意義。文獻[17]指出：單軸輪載作用在鋼軌上一般由5 根軌枕承擔，各軌枕分擔輪載的比分別為10%，20%，40%，20%和10%，如圖1所示，由于需要將列車的動力問題考慮在內，圖1中所示的列車輪載應動輪載，可由下式計算：

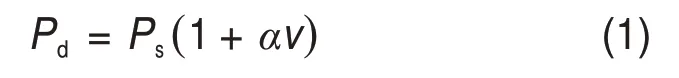
式中：Pd為單個動輪載，kN；Ps為單個靜輪載，kN；α為動力沖擊系數或速度影響系數；v為列車行駛速度，km/h，若v為300～350 km/h，則α=0.003，若v為200～250 km/h，則α=0.004；重載貨車的行駛速度一般為120 km/h，其α可取0.004。

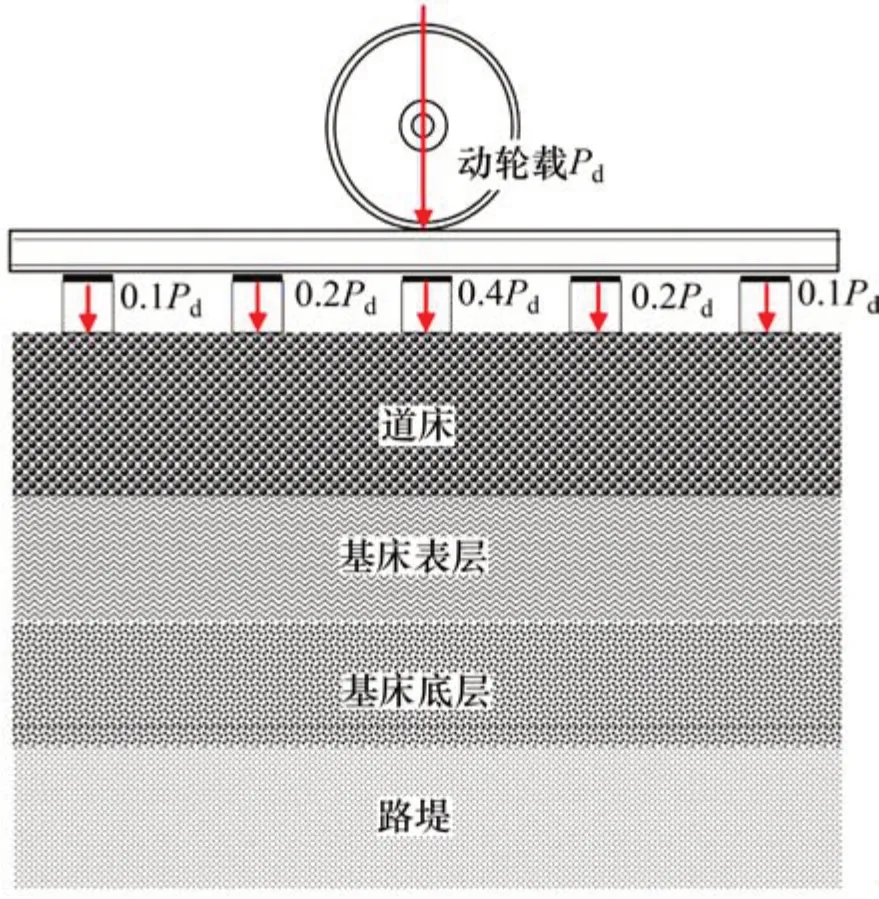
圖1 列車輪載在5根軌枕上分擔的示意圖Fig.1 Distribution of wheel load on five sleepers

盡管文獻[17]給出的方法具有使用方便、易于記憶的優點，且有一定的安全容許度，但應用時通常假設輪載恰好作用于軌枕正上方，而當列車輪載位于其他位置處時，各軌枕所承擔的輪載分擔比的確定較復雜。呂文強等[18]基于Winkler 彈性連續支撐梁模型，假定軌道結構為線彈性連續均勻分布，指出軌枕分擔輪載的比值與Gauss函數曲線形態相似，提出了如式(2)所示的Gauss函數表達的各軌枕分擔輪載比αi近似計算方法：

式中：σ為形狀參數；i為承擔列車輪載的軌枕編號；xi為編號為i的軌枕中點坐標；n為承擔列車輪載的軌枕數量，若列車輪載位于軌枕正上方，則n=5，若列車輪載位于兩相鄰軌枕中間的某一位置處，則n=6。

以列車輪載作用于軌枕正上方為例，采用Gauss 函數法計算軌枕荷載分擔比。假設60 kg/m的標準鋼軌由III 型鋼筋混凝土軌枕支承，其間距為0.65 m，1 km 鋪設1 539 根軌枕，此時n=5，則各軌枕的荷載分擔比計算結果如圖2所示。假定軌道結構為線彈性連續均勻分布，則隨著列車輪載移動，盡管列車輪載的位置發生了改變，但軌枕荷載分擔比的曲線形狀仍保持不變，表現為Gauss函數分布曲線隨著列車輪載的移動而平移。

1.2 多個列車輪載作用的軌枕荷載分擔比

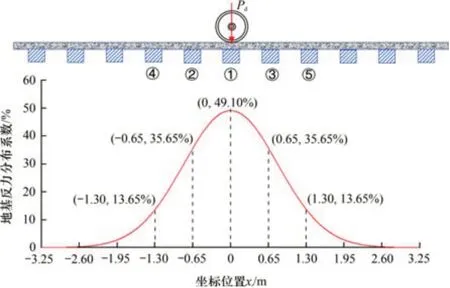
圖2 單列車輪載作用于軌枕正上方時的輪軌荷載分擔比Fig.2 Load sharing ratio of sleepers with single wheel acting above the sleeper

列車荷載由多節列車車廂的軸載組成，可認為是多個輪軸荷載，由于輪軸間距通常不大，道床-路基結構內部的應力場需要考慮各輪軸之間的相互影響。圖3所示為和諧號CRH3型電力動車組車廂結構示意圖，由圖3可見：1 個轉向架中2 個輪軸的間距為2.5 m，前后車廂相鄰轉向架的前后輪軸間距為5.0 m。由于單列車輪載作用于軌枕正上方時由5根軌枕承擔，影響長度為2.60 m；作用于2個相鄰軌枕之間時由6根軌枕承擔，影響長度為3.25 m。因此，1 個轉向架的2 個輪軸荷載存在荷載影響疊加區，而前后車廂2個轉向架之間不存在荷載的相互影響。

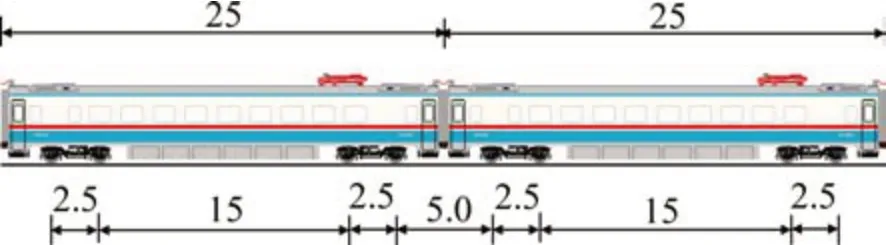
圖3 CRH3車廂結構示意圖Fig.3 Geometry of the CRH3 carriage

基于上述分析，對于CRH3 系列高速列車荷載，僅需研究1 個轉向架的2 個輪軸荷載的作用，本文主要考慮如下的2種情況：1)其中有1個列車輪載位于2個相鄰軌枕的中點處；2)其中有1個列車輪載恰好位于某一軌枕正上方。通過Gauss函數的疊加計算，可以分別計算2種情況下各軌枕的荷載分擔比，計算結果如圖4所示，其中，第1種情況下雙輪軸荷載將由其影響范圍內的10 根軌枕承擔，而第2種情況下的列車輪載將由其影響范圍內的9根軌枕承擔。

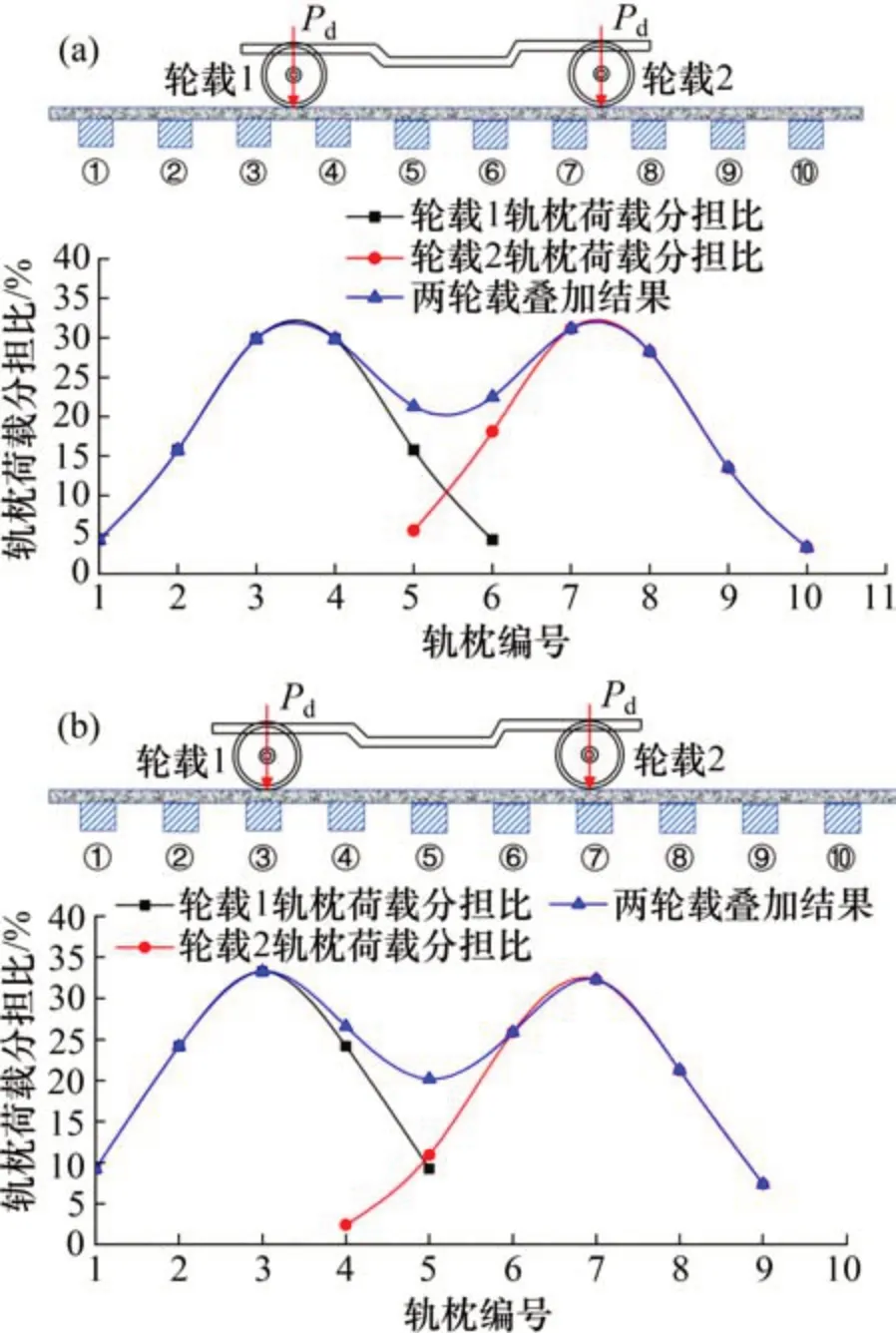
圖4 雙輪載作用于不同位置處的軌枕荷載分擔比Fig.4 Load-sharing ratio of sleepers when two with loads acting on different positions of rail

由圖4可知：在1 個轉向架的2 個列車輪載作用下，軌枕荷載分擔比沿轉向架的中心呈對稱分布，近似為“M”形。由于2 個輪載的相互疊加，導致轉向架之間區域的軌枕所承擔的荷載高于兩側軌枕承擔的荷載，但軌枕分擔比的最大值仍然位于列車輪載所作用的位置，且與單個列車輪載作用下的軌枕荷載分擔比最大值相同，表明基于本文所考慮的列車荷載情況，軌枕荷載分擔比的最大值沒有受到相鄰軸載的影響。同時可以看出，雙輪載作用于不同位置所引起的軌枕荷載分擔比不同，當荷載1位于相鄰軌枕中心時，轉向架之間范圍內軌枕荷載分擔比更為均勻，且最大軌枕荷載分擔比相對較小。由于輪載1作用于軌枕正上方的情況所對應的軌枕荷載分擔比最大，對于路基結構承載力設計更為不利。因此，后續研究將考慮第2種情況所示的雙輪荷載作用位置。

1.3 道床表面的列車輪載分擔規律

列車輪載依次由鋼軌傳遞到軌枕、道床，最終傳遞到路基結構表面的應力在軌枕的有效支承面積內均勻分布[19]，對于本文中的荷載工況，雙輪軸作用下道床表面的荷載分布規律示意圖如圖5所示。圖5中，b為軌枕的平均寬度；e為軌枕單側的平均有效支承長度，一般取為軌枕端部至鋼軌中軸線距離的2 倍，對于長度為2.6 m 的軌枕，軌枕單側的平均有效支承長度e為1.1 m。

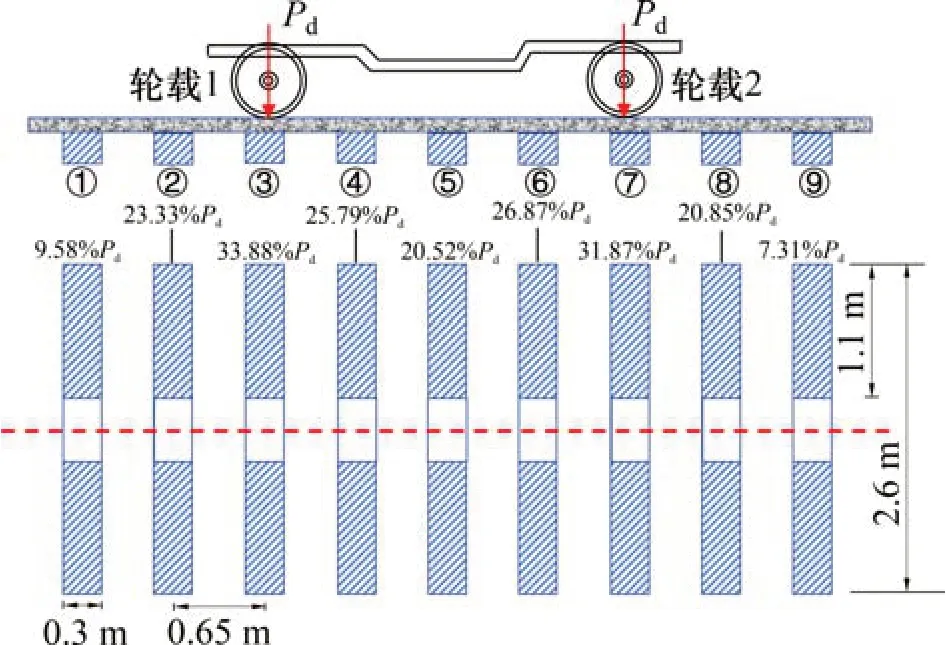
圖5 雙輪軸作用下道床表面的荷載分布規律示意圖Fig.5 Load distribution on the ballast surface under two wheel loads

2 單層道床結構的靜力安定解析方法

2.1 Melan靜力安定定理

Melan安定定理也稱為靜力安定定理：若存在一個與時間無關的自平衡殘余應力場σr ij，它與給定荷載范圍內的任意外荷載λp(p為單位荷載，λ為無量綱因子)所產生的彈性應力場σe ij相疊加后，處處不違反屈服準則f(·)，則結構是安定的，可表述如下：

式中：λSD為靜力安定荷載乘子，其中，第1 個表達式滿足了殘余應力場的自平衡條件，后2個表達式保證了彈性應力場與殘余應力場的疊加滿足屈服方程。

靜力安定荷載求解的關鍵在于準確獲得結構在外荷載作用下的彈性應力場以及構造與時間無關的最佳的自平衡殘余應力場。彈性應力場可以通過彈性力學原理或數值模擬方法求解，而構造理想的殘余應力場則相對較為困難。對于承受交通荷載作用的均質、各向同性半無限空間結構，YU[3]指出，由于其垂直于行車方向的截面受到相同的應力歷史，因此，所有的殘余應力分量均與交通荷載行駛方向(即x方向)無關，同時臨界點始終位于xz平面(即y=常數)，在此平面上，由于殘余應力場的自平衡條件和邊界條件，導致切應力因此，結構中可能存在的殘余應力分量為和，且這2個分量是有關y和z的函數。由此，安定荷載的求解就最終歸結為對殘余應力場的優化和對彈性應力場的精確計算。

2.2 多輪載下半無限空間中彈性應力場解析方法

2.2.1 單個均布荷載產生的角點處彈性應力場

根據BOUSSINESQ 解，假設豎向均布荷載p作用于長和寬分別為A和B的矩形區域，若以矩形荷載的角點O為坐標原點建立直角坐標系，在矩形荷載面上任意取一面積為dxdy的微小單元，則作用于該微小單元上的分布荷載可以用集中力pdxdy表示，通過積分可以求得O點下方任意點M(0，0，z)處由豎向均布荷載所引起的彈性應力分量，如圖6所示。

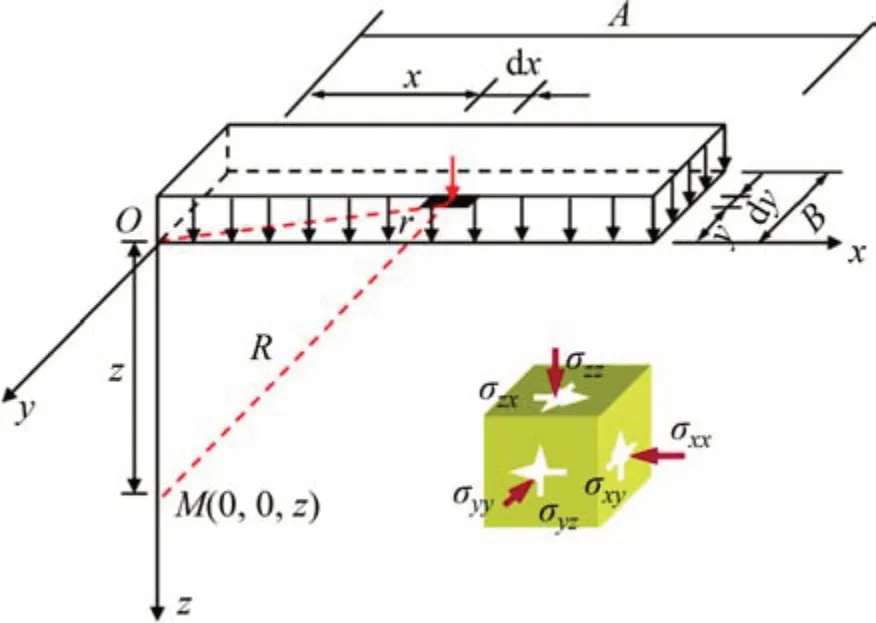
圖6 均布荷載下半無限空間中彈性應力場計算示意圖Fig.6 Elastic stress in half-space under uniform stress

在豎向均布荷載p作用下，沿O點以下任意深度處的彈性應力場推導結果為

由CERRUTI 彈性理論解，同樣可以得到在水平均布荷載q作用下的彈性應力場，推導結果如下：

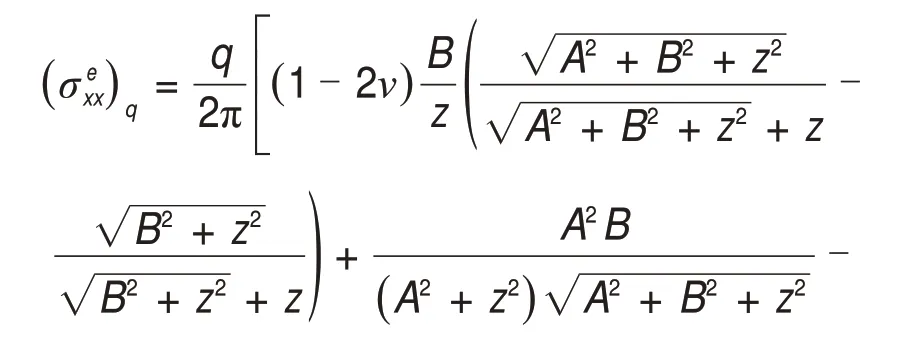
單個矩形均布荷載同時包含豎向荷載p和水平荷載q，且滿足q=μp(假設作用于半無限空間結構中的水平向荷載與豎向荷載呈線性關系，比例系數為μ)，則其在矩形荷載角點處產生的彈性應力場為

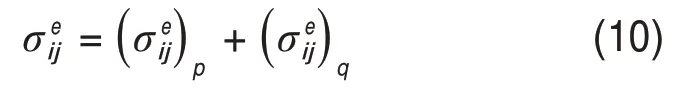
2.2.2 多個矩形均布荷載作用下的彈性應力場

假設第n個矩形荷載在半無限空間表面的角點坐標為(xn，yn,)，則對于表面任意點O(x，y)，根據其相對位置，可能出現如圖7所示的4種情況。在計算中可以通過O點分別作平行于矩形均布荷載長邊和短邊的平行線，將面積劃分成若干個區域，則O點就成為了各個區域的公共角點，分別計算每個矩形區域角點下同一深度z處的彈性應力場，然后，進行代數求和即可得到均布荷載作用于半無限空間任意深度處的彈性應力場。

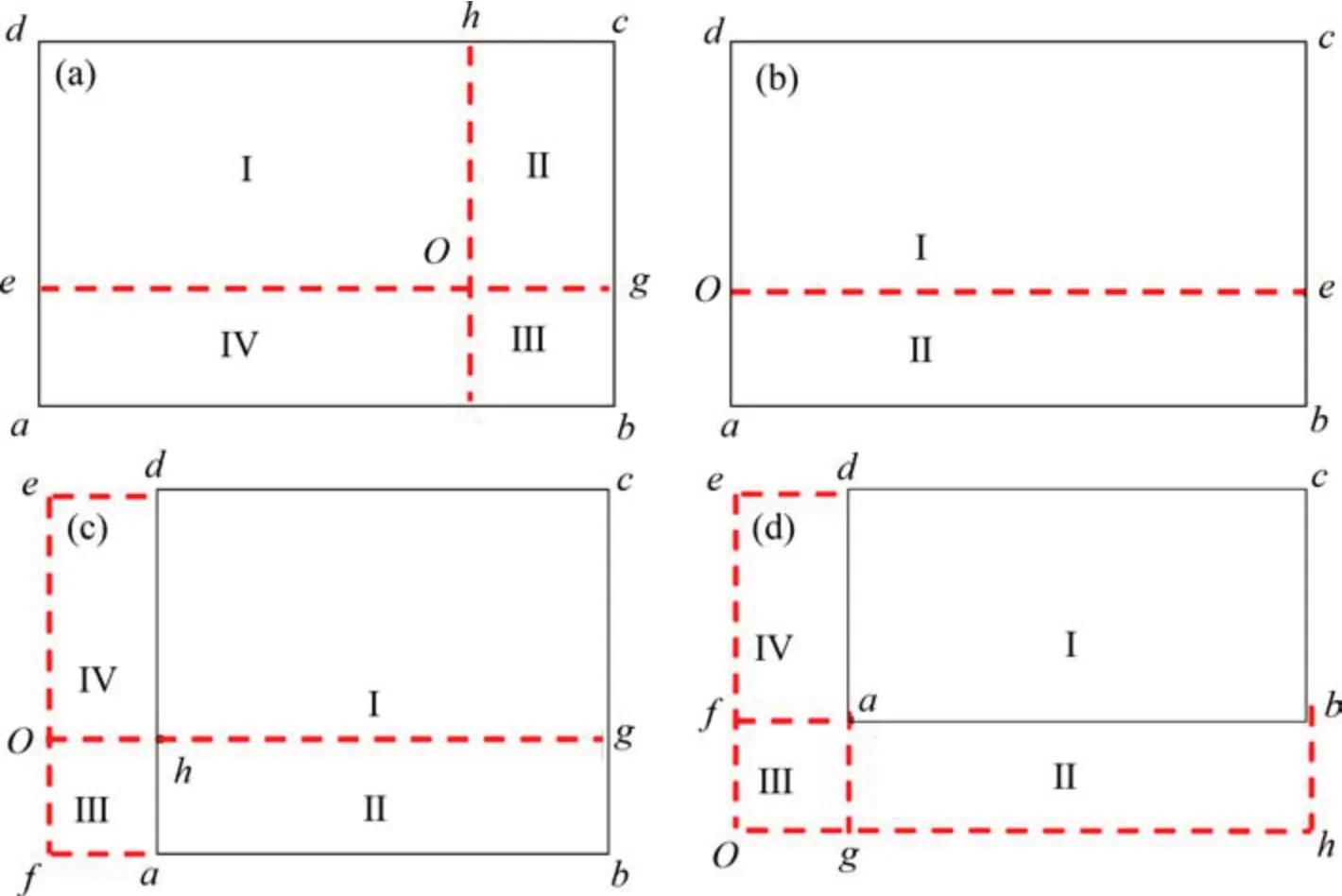
圖7 角點法計算彈性應力場的4種情況Fig.7 Four situations of corner points method for calculation of elastic stress field

對于多個均布荷載作用的情況，若荷載數為m，則由該m個均布荷載在半無限空間體內部任意點處產生的彈性應力場可以由疊加原理得到：

2.3 彈性應力場結果分析

列車輪載由鋼軌和軌枕傳遞到道床表面的應力為均勻分布，且作用面積為軌枕的有效支承面積，單根軌枕的有效支承面積為2個大小相同的矩形荷載，與軌枕中心線呈對稱分布。為簡化分析，僅考慮半根軌枕的有效支承面積，分析彈性應力場。圖8所示為單個軌枕作用于O點的彈性應力場示意圖。考慮半根軌枕的有效支承為0.3 m×1.1 m(圖8中虛影部分)，分別施加100 kPa放入豎向和水平均布荷載，可得到O點以下z深度處的彈性應力場結果如圖9所示。由圖9可見：在單個荷載作用下，本文所推導的豎向應力的計算公式與土力學中的角點法完全一致。在半無限空間表面處，僅荷載作用區域范圍abcd內有荷載存在，其他區域的所有彈性應力分量均為零，隨著荷載向深處擴散，呈現出應力泡現象。因此，豎向應力沿O點先增大，然后減小，逐漸趨于零。

圖8 單個軌枕作用于O點的彈性應力場示意圖Fig.8 Elastic stress filed at point O under stress acting on single sleeper

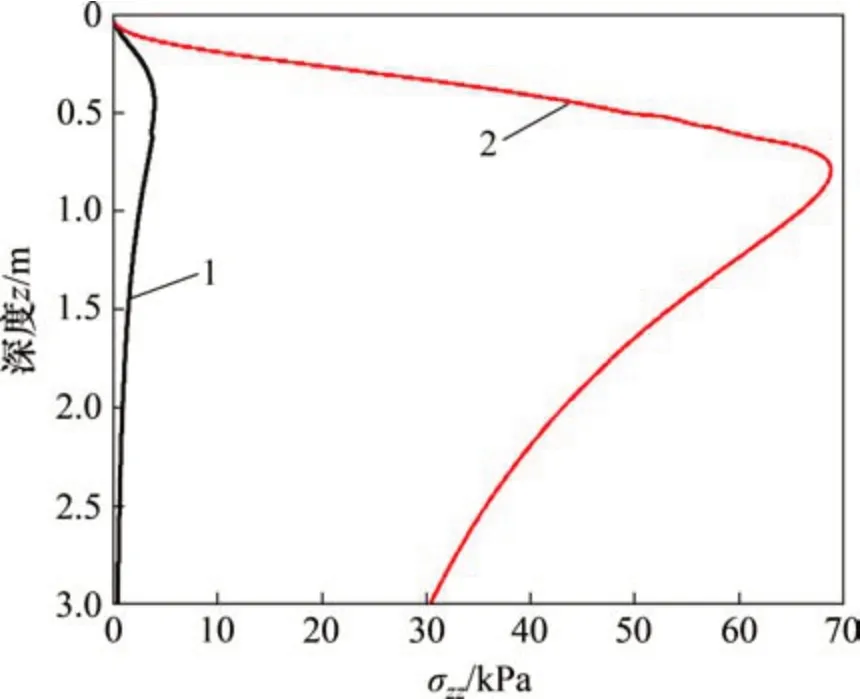
圖9 水平和豎直均布荷載作用下沿O點豎向應力計算結果Fig.9 Vertical stress along point O under horizontal and vertical distributed stress

考慮平面尺寸為3 m×3 m 的半無限空間結構，在其表面的中心區域施加如圖8所示的呈平行分布2 個矩形均布荷載，沿y方向的間距為0.65 m，其中豎直和水平荷載均為100 kPa，則可得到如圖10所示的深度z=0.5 m 處的各彈性應力分量計算結果。由圖10可見：在2 個豎直與均布荷載作用下的彈性應力場相互影響，數值上相互疊加，且相對于2個荷載中軸線呈對稱分布。由此可知：多個荷載作用所引起的彈性應力場必然在半無限空間結構中相互影響，而表現出與單荷載不同的彈性應力分布規律。因此，僅考慮單個荷載作用的安定分析不能準確反映結構的實際承載能力，必須針對結構的受力特點，考慮如圖5所示的更為實際的荷載情況。

3 單層道床結構安定分析

考慮如圖5所示的荷載分布形式，基于式(3)，結合上述推導的均布荷載作用下半無限空間結構中的彈性應力場解析解，通過Matlab 編程可以求得單層道床結構的靜力安定荷載λSD，安定荷載的具體求解過程及殘余應力場的優化過程見文獻[15]。

3.1 安定解析方法的驗證

為了驗證均布荷載作用下解析方法的正確性，本文考慮單個均布荷載作用，以歸一化的靜力安定荷載λSDp0/c作為分析內容，將計算結果與已有研究結果進行對比，結果如圖11所示。由圖11可見：本文的計算與SHIAU[20]基于均布荷載的計算結果規律基本一致，結果也較接近，最大誤差為10%。由于有限元方法的離散性，所得到的安定荷載為精確安定荷載解的近似值[20]，因此，本文存在的誤差具有合理性，驗證了計算方法的合理性與可靠性。

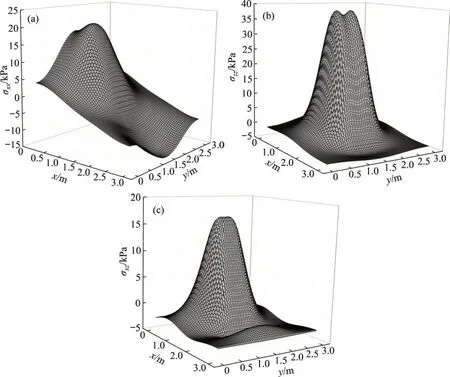
圖10 2組豎直和水平均布荷載共同作用下的彈性應力場(z=0.5 m)Fig.10 Elastic stress field under two uniformly distributed horizontal and vertical stresses(z=0.5 m)

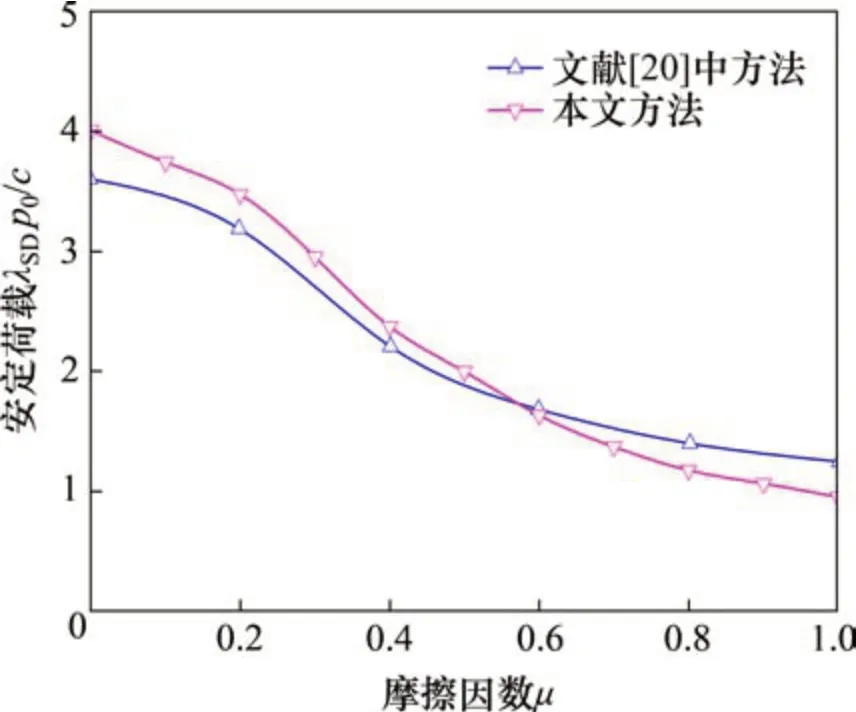
圖11 均布荷載作用下的靜力安定解析方法的驗證結果Fig.11 Validation of the lower-bound shakedown solution under uniform stress

3.2 參數敏感性分析

假設道床材料服從Mohr-Coulomb 屈服準則，基于本文推導的均布荷載作用下的彈性應力場的求解方法可計算單位荷載p0作用下的彈性應力場，由Melan靜力安定分析方法經簡單的數值規劃，可求解得到單層半無限空間結構的靜力安定荷載乘子λSD。需要注意的是，本文中單位荷載p0為作用于圖5的9根軌枕等效作用面積內的荷載總和，通過不同的荷載分擔比計算得到相應軌枕等效作用面積上所承擔的荷載。對于道床材料，在安定計算中考慮內摩擦角φ為45°，黏聚力c為5 kPa，泊松比v為0.3。為了盡可能全面分析道床材料的安定行為，本文分析了安定荷載的參數敏感性，選取道床內摩擦角φ的變化范圍為25°～75°，泊松比v變化范圍為0.10～0.49，歸一化的靜力安定荷載λSDp0/c計算結果如圖12所示。

圖12 道床材料參數對靜力安定荷載的影響規律Fig.12 Influence of material properties of ballast on static shakedown load

由圖12(a)可見：在給定的摩擦因數μ下，隨著道床內摩擦角φ增大，靜力安定荷載λSDp0/c幾乎呈指數函數增長，對于μ=0的情況，道床內摩擦角由25°增大到75°導致道床結構的靜力安定荷載增大了7.25 倍，說明材料內摩擦角增大可明顯提高結構的承載能力。摩擦因數μ與作用在道床表面的切向荷載緊密相關，當μ增大時，結構所承擔的荷載也相應增大，因此，摩擦因數μ降低了結構的靜力安定荷載，當摩擦因數由0 增大到0.5 時，道床結構的靜力安定荷載減小75%～88%。

由圖12(b)可知：當摩擦因數μ≤0.2時，靜力安定荷載隨著泊松比增大而增大，當μ>0.2時，靜力安定荷載隨著泊松比增大而減小，但總體變化幅度均在1%以內，表明盡管泊松比v是彈性應力場的重要參數，但其對道床結構靜力安定荷載的影響相對較小。

4 結論

1)對于CRH3系列高速列車荷載，僅在1個轉向架的2個輪軸荷載之間存在疊加影響，在其影響范圍內軌枕荷載分擔比呈現“M”形分布。

2)通過與已有文獻計算結果的對比，驗證了本文推導的彈性應力場解析方法及靜力安定分析方法的可行性和計算結果的準確性，可為安定理論在具體工程實際中的推廣應用提供參考和理論依據。

3)道床結構的靜力安定荷載隨內摩擦角增大而增大，盡管泊松比是影響結構彈性應力場的重要參數，但其對道床安定荷載的影響較小，在滿足經濟性的前提下，適當選用高強度的材料，能有效提高給定摩擦因數下道床結構的承載能力。