打造開放的小學數學課堂

徐正洲

摘要：學之道在于“悟”，教之道在于“導”。學生學習應該是“教”和“學”的相互滲透、相互促進。小學數學常態課堂開放式教學的實踐過程正是學生“悟”與“行”的研究活動。教師要聚焦開放學習現場，做好“引”和“導”的服務，充分挖掘開放資源，促進學生思維發展。《平均數》一課教學，嘗試開放式教學：讓學生通過套圈比賽生成數據，從“一組數據的整體水平”來認識平均數，感悟意義，構建概念。

關鍵詞：小學數學開放式教學《平均數》

課程改革在不斷深化中持續推進，課堂教學樣態呈現從“教”為中心向“學”為中心、從封閉向開放的積極轉變。對此，我們開展了小學數學常態課堂開放式教學探索：突出學生的主體地位，重視學生主動參與學習內容的建構，強調學生個體潛能的充分發揮，培養學生敢于面對“沒有現成答案的問題”，尋求解決方法和策略，鼓勵學生提出問題并解決問題，發揮學生的個體智慧，發展學生遇到學困之處、學難之處借助團隊智慧合力解決問題的能力，促進學生思維和能力的發展。

“平均數”是發展小學生統計觀念的核心內容之一。從整體上來看，傳統教法偏重讓學生通過計算一組數據的平均數，即從算法的層面理解平均數的意義，片面地將“平均數”學習弱化為一種簡單的技能訓練，忽視了統計學意義上的理解與把握。對此，教學《平均數》一課時，實踐開放式教學：讓學生通過套圈比賽生成數據，從“一組數據的整體水平”來認識平均數，感悟意義，構建概念。具體教學過程如下：

一、比賽導入，認知開放

本節課，蘇教版小學數學教材設置了套圈比賽情境，雖然十分貼近學生的生活，但畢竟只是圖表和文字的呈現，始終會與學生隔著一層膜。對此，采用開放式教學，讓學生親身體驗套圈比賽，生成數據。這樣不僅能點燃學生的學習熱情，還能利用學生的勝負心持續激發他們探究的欲望。切身體驗更容易激發學生的認知共鳴，有時一個學生的發言還能引發一群學生的思考和爭論。

（課始，教師組織學生進行套圈比賽：分成男生組和女生組，每人套10個圈，記錄相關數據。）

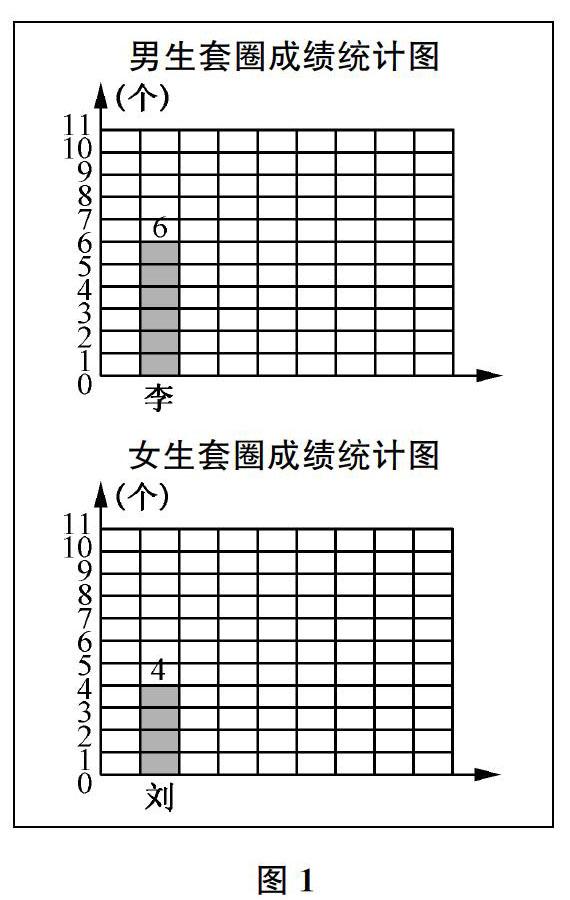
師剛才的套圈比賽非常激烈，老師選取了其中幾組數據。（出示圖1）這是第一個出場的男生和第一個出場的女生的套圈成績，誰套得準？

1

生男生套得準。

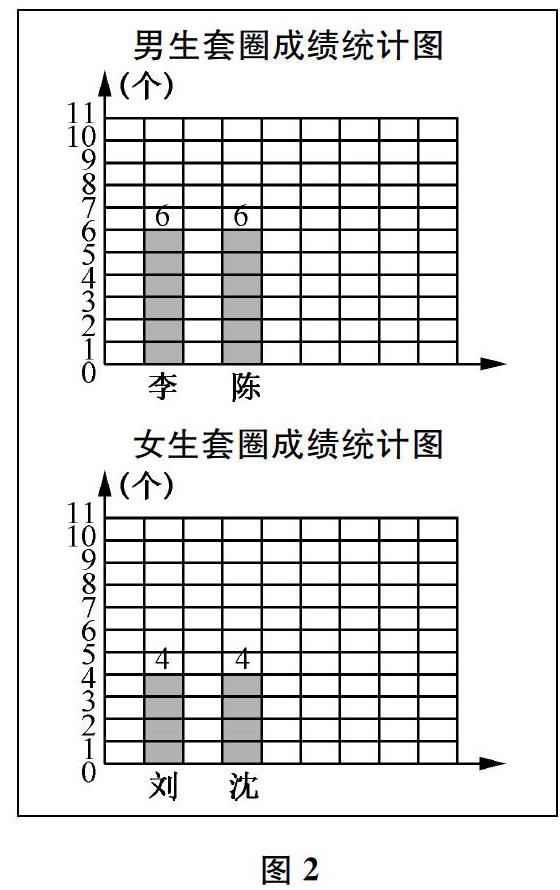
師（出示圖2）繼續看。現在是男生還是女生套得更準一些？

生還是男生。他們一共套了12個，女生一共只有8個。

師你是比男女生兩個人一起套的總數。

生男生每個人套的都是6個，女生每個人套的都是4個，只要比一個人的成績就行了，所以男生準一些。

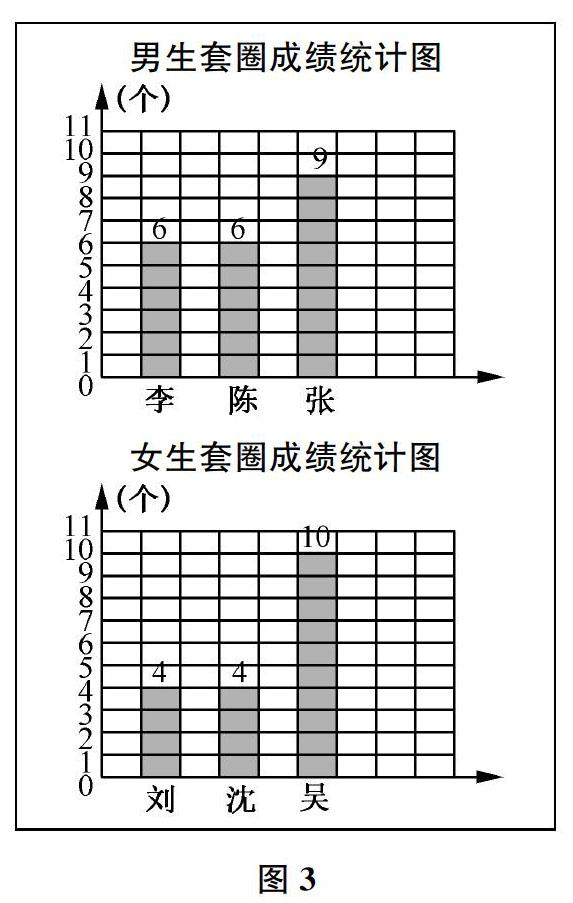
師你是比一個人的套圈成績，因為男女生兩個人的成績相同。（出示圖3）每組都比了三個人，現在男生套得準一些還是女生套得準一些？

生女生最多套中10個，我覺得女生套得準一些。

生我覺得只比每組最多的一個人套中的個數不合理。

生我也覺得不合理。你想想呀，第三個女生就比第三個男生多1個，但兩組前兩個人卻相差更多。

師還有不同的想法嗎？

生他們人數一樣多，我覺得可以比套中的總數。

生我同意他的說法。男生套中了6+6+9=21（個），女生套中了4+4+10=18（個），所以男生準一些。

師是啊，當男生、女生人數相等時，可以直接比較他們套中的總數。

生老師，如果男生和女生人數不一樣多，又該怎么比較呢？

師你這個問題特別有價值！大家認為該怎么比？

最后一位學生的提問特別有意義，能夠引發其余學生的思考，推進課堂深入。這也正是開放式教學想要達成的效果。在學生提問后，教師并沒有直接給出答案，而是把問題拋給學生，暴露學生的初衷，使其在豐富多元的解決方案中尋求教學的新起點。

二、研學匯報，思路開放

教學難點的突破是一節課最為關鍵之處，教師要敢于放權、放手，讓學生主動出擊，通過個人獨學、小組研學等方式尋求解決方法。教師負責提供交流討論的機會，引導學生把握問題解決的契機，同時提供必要的學習幫助，于疑難處給予精當的點撥、提示和引領，促進學生數學思維的發展。

開放式教學的課堂中，四人互學小組的研學是關鍵。因為解題思路的不唯一、問題答案的不唯一，學生需要在小組內充分表達自己的所思所想，在交流中碰撞思維、激發靈感，在討論中求同存異，在辯論中達成共識;遇到困難之處，需要借助全班同學的智慧，或向老師尋求幫助，展開研究性學習。

匯報環節，是開放式教學為學生搭建的暢所欲言、表達思考的舞臺。匯報的總體要求是：認真聽取不同小組的完整思考過程，和本組的研討成果進行比較，了解異同點;有理有據地說明自己的觀點，敢于堅持自己的觀點;勤于思考，敢于對錯誤意見提出質疑，能夠說明錯誤的理由。

師（出示圖4）現在，你覺得是男生套得準一些，還是女生套得準一些？先獨立思考，如果有困難，可以在小組里商量商量。

生我覺得可以比總數，6+6+9+6=27（個），10+4+7+5+4=30（個）。所以，女生套得準一些。

師女生同意嗎？

生（女生齊）同意。

師那男生呢？

生（男生齊）不同意。

師你們為什么不同意？

生（男生）因為這樣不公平，男生4個人，女生5個人。

師那“單挑”？

生也不公平，剛才就討論過了。

師那用什么樣的方法比較才公平呢？

生我們可以移一移，使男生的個數相等，女生的個數也相等，再比較。

師好辦法！還有別的想法嗎？

生比男、女生平均每人套中的個數。

師具體怎么比呢？

生先算出小組同學共套中的個數，再除以小組人數。

師對，用這種方式計算出來的就是小組同學的平均套圈水平。想一想，平均數是一種數嗎？

生不是吧，平均數是一組數的平均水平。

生平均數是一組數的整體水平，有的同學達不到這個水平，也有的同學會高于這個水平。

生是為了方便比較才想出的一種辦法。

師是的，平均數反映了一組數的整體水平。

從相同人數到不同人數的小組套圈水平比較方法躍升，是學生理解上的難點。對這一難點的有效突破必須建立在學生的自主理解之上，即通過現實情境生發認識沖突，在不同觀念的碰撞中深化學生自我的省思，進一步明確單純比總數的欠缺與不足，從而讓平均數概念的產生成為認知需求。在此基礎上，繼續理解“平均數代表一組數的整體水平”。

三、練習開放，融通所學

效度適合的針對性練習不僅能讓教師有效了解學生新知學習的真實狀態，檢驗學習成效，還能讓學生鞏固新學，拓展延伸新知，促進知識的內化與知識體系的建構。教師要對教材提供的習題資源進行二次開發，增加開放性元素，擴展開放的維度，讓學生學會多方位、多角度、多層次地思考問題，采用不同的方法解決問題，并通過比較，發現最有效的解決方法，從而發展思辨能力，提升求異思維品質。

師（出示圖5）不計算，猜一猜，三根彩帶的平均長度可能是多少？

生15厘米。

生17厘米。

生20厘米。

生比最短的14厘米長，比最長的24厘米短。

師那究竟是多少呢？請同學們算一算。

生平均長度是18厘米。

師如果想要三根彩帶的平均長度是20厘米，有什么辦法可以辦到？

生把每一根彩帶的長度都增加2厘米。

生把其中一根彩帶的長度增加6厘米。

生可以把14厘米長的彩帶增加到20厘米。

師同學們，你們的方案都是正確的。如果讓你們繼續說下去，還有其他方案嗎？（生齊答：有）是的，還有很多種符合要求的方案。其實，這些方案都有一個相同點，就是要想方設法將三根彩帶的總長度增加——

生6厘米。

師是的。老師要為你們“點”個大大的“贊”！

緊扣平均數的意義理解，對教材中的習題進行合理的“再開放”，改變問題的設問方式，從三根彩帶平均數的范圍確定到平均數增加后彩帶長度的變化，給學生的思維發展提供更廣闊的實踐場，幫助他們達成了意義理解基礎上的抽象思維發展。

學之道在于“悟”，教之道在于“導”。學生學習應該是“教”和“學”的相互滲透、相互促進。小學數學常態課堂開放式教學的實踐過程正是學生“悟”與“行”的研究活動。教師要聚焦開放學習現場，做好“引”和“導”的服務，充分挖掘開放資源，促進學生思維發展。

*本文系江蘇省教育科學“十三五”規劃重點資助課題“數學開放題融入小學常態課堂的研究”（編號：Ba/2016/02/14）的階段性研究成果。

參考文獻：

[1] 楊傳岡.小學數學開放題教學行思[J].教育探索，2015（11）.

[2] 楊傳岡.局限于知識傳授，還是著力于學生認知需求——以蘇教版三下《平均數》為例[J].新教師，2013（9）.

[3] 楊傳岡.數學開放題教學重在“開放”[J].教學與管理，2016（26）.

[4] 戴再平，孫聯榮，凌國華，等.數學開放題研究[M].南寧：廣西教育出版社，2012.