礦山深部巷道圍巖變形與應力分布數值模擬研究

（河南工業和信息化職業學院，河南 焦作 454000）

在礦山深部工作中，由于礦山深部地形復雜的特點確保礦山深部巷道圍巖的安全一直是礦山支護工作中最為薄弱的環節，因此長期以來受到同行學者們的重點關注[1]。在礦山開采過程中由于受到人為因素的影響，改變礦山深部巷道圍巖結構，從而使礦山深部巷道圍巖很容易發生變形，礦山深部巷道圍巖變形容易引發安全事故問題，直接威脅礦山工作人員的生命安全。本文在此基礎上，展開礦山深部巷道圍巖變形研究，并通過應力分布數值模擬致力于精準掌握礦山深部巷道圍巖變形情況，確保礦山深部巷道圍巖的安全性。

1 礦山深部巷道圍巖變形

在礦山深部開采過程中，原巖應力受開采影響會改變巖體的平衡狀態，導致變形。礦山深部巷道圍巖變形具體特征，如表1所示。

表1 礦山深部巷道圍巖變形具體特征

結合表1所示，本文通過三方面分析礦山深部巷道圍巖變形特征，為礦山深部巷道圍巖支護工作的順利開展提供理論依據。

1.1 巷道頂板的變形破壞

在礦山深部巷道頂板開挖過程中，巷道頂板由于受到應力產生瞬時彈性變形，并在變形時引發一系列其他繼續變形[2]。在開挖后，巷道頂板的拉應力會集中致使圍巖張拉破壞。這樣一來，導致巷道頂板很難處于穩定狀態，尤其在自重作用的促使下，巷道頂板的水平方向發育極其柔弱，形成數量、大小、形狀各不相同的分離體。巷道頂板的變形破壞可以按照載荷方向分為：垂直載荷變形破壞以及水平載荷變形破壞，由于破壞方式的不同，巷道頂板的變形破壞所受載荷也必然不同。因此，在分析礦山深部巷道圍巖變形時，必須考慮巷道頂板變形破壞的載荷方向。

1.2 角部破碎

礦山深部巷道圍巖變形中，最先發生變形的區域往往在巷道圍巖的四個邊角處。考慮到礦山深部巷道圍巖一般在比較狹窄的區域，因此只要一個角部出現破碎的情況，就會導致整個巷道圍巖失穩，產生應力破壞，導致礦山深部巷道圍巖變形。

1.3 巷道底膨破壞

巷道底膨指的是礦山深部巷道圍巖的最底層，通常情況下為軟弱巖層，在砂頁巖互層層理的情形下導致巷道底膨破壞。結合冷建民等人提出的三山島金礦深部巷道圍巖破壞機理及支護參數優化中表明，影響巷道底膨破壞的直接因素為巷道底層的泊松比。當泊松比取值為0.5時，礦山深部巷道底板的擠壓應力與豎直應力基本處于持平狀態，此時壓力系數為1。但一旦出現巖體的強度小于擠壓應力時，就會造成巷道底膨破壞，進而引發礦山深部巷道圍巖變形。

2 礦山深部巷道圍巖應力分布數值模擬

考慮到礦山深部巷道圍巖變形的各種形式，本文從礦山深部巷道的破壞模式入手，基本假定礦山深部巷道應力分布符合張拉剪切組合的Mohr-Coulomb準則，并且能夠充分考慮到模擬圍巖與支護結構之間的相互作用關系。在此情況下，分析模擬圍巖與支護結構失效的破壞機理與過程，進而總結推導礦山深部巷道應力分布計算公式。最后，對礦山深部巷道應力分布數值模擬結果展開分析。

2.1 確定礦山深部巷道圍巖應力應變關系

本文進行基本假定的具體內容包括：礦山深部巷道模擬圍巖在應力應變過程中必須保持平面形態；排除由于抗拉強度的不同導致對數值模擬造成的誤差值；在發生礦山深部巷道應力應變時，礦山深部巷道圍巖變形應力與彎曲應變呈理想彈塑性關系，一旦承載力失效應力即保持不變以及礦山深部巷道圍巖應力應變關系。可以將礦山深部巷道圍巖應力應變關系視為一種曲線關系，如圖1所示。

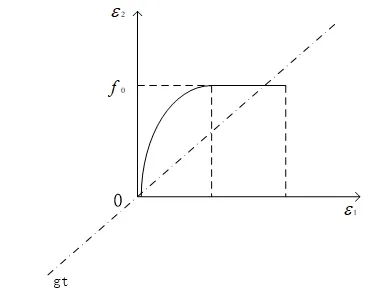
圖1 礦山深部巷道圍巖應力應變曲線圖

在圖1中，ε1指的是礦山深部巷道圍巖應力直線部分合力；ε2指的是礦山深部巷道圍巖應變直線部分合力；f0指的是應力應變曲線中二次拋物線礦山深部巷道圍巖變形部分合力；gt指的是相關流動法則。通過圖1可知，當礦山深部巷道圍巖變形呈現雙向應力狀態時，圍巖變形承載力必然會隨著另一向圍巖變形應力的增加而降低，直至圍巖變形承載力失效。在得出圍巖變形應力應變線性關系的基礎上，可以根據計算結果曲線，總結出圍巖變形抗壓強度的計算公式。可以通過計算雙向應力狀態時，圍巖變形的抗壓強度，為下一步理論計算礦山深部巷道圍巖應力分布做準備。設圍巖變形的抗壓強度為σ，則其計算公式，如公式（1）所示。

在公式（1）中，β指的是圍巖所能承受的最大拉應力。根據多次計算，設圍巖變形的抗拉強度為fc通常情況下為圍巖變形抗壓強度的10.5%～12.2%。因此，可以將圍巖變形的抗拉強度模擬為：

2.2 理論計算礦山深部巷道圍巖應力分布

對應圖1中，根據二次拋物線終點所對應的應變值，計算二次拋物線的高度即為圍巖應力在應變值下的承載力。設圍巖應力在應變值下的承載力為y，則其計算公式，如公式（2）所示。

在公式（2）中，x指的是圍巖應力截面面積；r1指的是圍巖應力的張拉強度。將得出的圍巖應力分布在應變值下的承載力代入靜力平衡條件可得，礦山深部巷道圍巖應力分布計算理論模型M，如公式（3）所示。

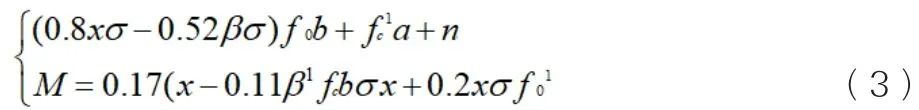
在公式（3）中，b指的是礦山深部巷道圍巖應力的摩擦角；a指的是粘聚力；n指的是膨脹角度，為實數。通過礦山深部巷道圍巖應力分布理論計算模型中的自變量可以得出礦山深部巷道圍巖應力分布的主要影響因素為礦山深部巷道圍巖應力的摩擦角、粘聚力以及膨脹角度。礦山深部巷道圍巖應力分布計算理論模型的整個計算過程均是以圍巖應力分布平截面的假定作為基礎，也就是說圍巖應力分布截面各點應變與中和軸的距離必須為正比例，圍巖應力分布應變與外圍相應處的應變一致，在縱向受拉圍巖應力達到屈服強度之前，截面的平均應變應該達到瞬間的平衡，以符合圍巖應力分布平截面的假定。依據此假定，再結合靜力平衡條件，建立了正截面圍巖應力分布承載力的計算體系。為驗證礦山深部巷道圍巖應力分布計算理論模型的合理性，選取礦山深部巷道圍巖，將得出的礦山深部巷道圍巖應力分布數值模擬結果與實測圍巖應力分布進行對比。從計算理論上來講，利用FLAC3D內置的結構單元錨索單元（cable）來模擬巷道圍巖支護中的錨桿和錨索，保證了礦山深部巷道圍巖應力分布得以充分發揮，導致由于錨桿（索）與圍巖的接觸粘結性退化，應力逐漸均勻化，緩和了礦山深部巷道圍巖應力軸向位移相應有軸向力，在一定程度上對模擬礦山深部巷道圍巖應力分布是有利的。在本次模擬中，通過HISTORY命令設置變量來確定某處斷面的位移變化和受力狀態，也可以判斷模型是否達到平衡或者破壞狀態。因此，礦山深部巷道圍巖應力分布數值模擬結果與實測圍巖應力分布基本一致。

3 結束語

考慮到礦山深部巷道圍巖變形問題的受到重視，礦山深部巷道圍巖應力分布數值模擬經歷了從起步到快速發展的階段。

因此，本文對礦山深部巷道圍巖變形與應力分布數值模擬研究是具有現實意義的，能夠為解決礦山深部巷道圍巖變形問題提供理論支持。

希望通過本文分析，為提高礦山深部巷道圍巖安全性方面提供參考，以促進國家礦業的可持續發展。但本文唯一不足之處在于，沒有對礦山深部巷道圍巖變形控制技術進行深入分析，相信這一點，可以作為礦山深部巷道圍巖變形領域日后的研究內容之一。