分時階梯電價下流水車間節能調度問題研究

閆建濤，肖繼明

（西安理工大學 機械與精密儀器工程學院，西安 710048）

0 引言

工業部門消耗的能源占到了全球能源消耗的一半，而工業中90%的電力都是由制造業消耗的。電能作為制造業的主要能源，如何節約電能是制造業不得不考慮的問題。合理的生產調度是可以降低電能消耗、降低生產成本的有效途徑之一[1]。為了維護電網穩定，不同的電價政策被實施，引導著電力用戶改變其電力消費模式[2]。考慮不同電價政策的生產調度可以在不減少產出的情況下，達到企業降低電力成本的目的。

傳統的生產調度側重于提高生產效率，是以最小化最大完工時間、成本、交貨率等為優化目標，近十年來，考慮能耗的生產調度成為了國內外學者研究熱點之一。李龍[3]等以車間的生產運作時間，生產成本以及車間能耗為目標，采用遺傳算法解決了流水車間綠色生產調度問題，并以流水車間齒輪類零件加工為例，驗證了模型的有效性與準確性。孟磊磊[4]等針對不相關并行機調度問題，以能耗最小化為目標，建立5個考慮關機/重啟策略的混合整數規劃模型，并對比分析了模型的優缺點。Zhang[5]等在考慮機器的加工速度基礎上，以加工過程的總加權延遲時間最短和總能耗最小為目標建立模型，并采用多目標遺傳算法對其求解。lei[6]等研究了在給定總能耗的情況下，使得完工時間和總延遲時間最小，對柔性作業車間進行建模，并采用帝國競爭算法對問題求解。

分時電價政策是促使電能需求曲線趨于平衡，減少高峰時段用電的一項電力措施[7]。考慮分時電價的生產調度可以改變用電時段，進而有效的減少生產所需的電力成本，達到降低能耗的目的。吳宇娟[8]研究了分時電價下，以最小化總用電成本為目標的相同并行機調度問題，建立了連續時間混合整數線性規劃模型，采用禁忌搜索-多級過濾貪婪插入啟發式混合算法對問題求解。Moon[9]以最小化完工時間和最小化電力成本為目標，并使用混合遺傳算法解決了考慮分時電價的無關并行機調度問題。Zhang[10]研究了分時電價下混合流水車間的調度問題，建立了機床的能耗模型，以最大完工時間和電力成本最小化為目標，采用改進的強度Pareto進化算法進行求解。Wang[11]研究了雙機流水車間調度問題，以分時電價下的總電力成本最小化為目標，將問題表示為混合整數線性規劃，然后基于Johnson規則和動態規劃方法設計兩種啟發式算法對問題進行求解。Mao[12]在分時電價下針對并行機調度問題，建立了經濟批量調整和調度模型，其目標是最小化生產中的電力成本，實現最優的經濟調度，最后通過實驗結果證明了所提出的模型顯著降低了電力成本，并促進了電網的峰值負荷調節。

從已有研究來看，大多數學者都只考慮了分時電價，并對不同的調度車間問題進行了建模求解，有效的降低了能耗。但僅考慮分時電價有其局限性，可能會導致峰谷時段的偏移，分時階梯電價作為一種新的基于價格的需求側管理措施被提出[13,14]，是在分時電價的基礎上加入了階梯電價，結合了分時電價的特點（均衡峰谷時段用電量）和階梯電價的特點（激勵用戶節能，提高能源利用率），可以更有效地促進用戶節能。

流水車間是常見的一種車間生產方式，在復雜度上，2臺機器以上的流水車間調度問題被證明是NP-hard問題[15]，因此本文針對流水車間的節能生產調度問題，考慮分時階梯電價，采用連續時間建模方式，建立生產調度的數學模型，設計算法進行求解，并通過實例驗證所建數學模型的正確性以及求解算法的有效性。

1 問題描述

考慮分時階梯電價的流水車間問題描述如下：有多個多種類的待加工工件，需要依次經過相同的工序進行加工，但不同種類的工件加工時間各不相同，每道工序只有一臺機器可以加工。已知工件各道工序在各機器上的加工時間和功率需求，要求在考慮分時階梯電價的情況下，確定工件的加工順序及每道工序的開始加工時間，保證在規定的時間內完成加工任務，同時使得加工消耗的電力成本最小。

分時階梯電價[14]按照電力用戶的用電習慣劃分時段，將一天時間分為高峰段、平段、低谷段三個時段，并在每個時段設定多級階梯電價，以兩級階梯電價為例，在低于用電量標準時執行第一階梯電價，高于用電量標準時，超出部分執行第二階梯電價，如圖1所示。

圖1 分時階梯電價示意圖

針對該問題進行如下假設：1）同一時刻，每臺機器只能加工一道工序；2）每道工序的加工時間是確定的；3）加工是非搶占式的，每道工序一旦開始加工不能中斷；4）夾具裝卸等準備時間計入每道工序的加工時間；5）工件的工序固定，每道工序必須在其緊前工序完成之后才能進行后續工序。

2 模型建立

為建立考慮分時電價的流水車間調度模型，引入數學符號定義如下：

n：待加工工件總數；

m：加工設備數，即工件的加工工序數；

s：分時電價劃分時段總數；

i：機器編號，i∈[1，m]；

k：工件編號，k∈[1，n] ；

j：加工時段編號，j∈[1，s]；

Ej：加工時段j的耗電量；

Pik：工件k在機器i上的加工時間；

qik：機器i加工工件k時所需功率；

Sik：工件k在機器i的開始加工時間；

Eik：工件k在機器i的加工完成時間；

Emax：最大完工時間；

ST：計劃開始時間；

ET：計劃結束時間；

PCSjv：j時段第v檔階梯用電量的分界點（單位：千瓦時）；

Pjv：j時段的第v檔電價，v∈[1，V]；

如何實現這一突破，實現華裔青少年族群意識的恢復、華族文化的認同、華語能力的掌握及華語水平的提高，數年來一直是老一輩華族、中國政府及華文教育者所思考的問題。中國國務院僑辦“尋根之旅”活動的推出，為我們提供了一條解決這一難題的極好途徑。俗語說：讀萬卷書，行萬里路，百聞不如一見。“中國尋根之旅”就是培養文化認同最直接、最有效的途徑之一。因為，開展此類活動，可以讓華裔青少年身臨祖籍國，通過耳聞目睹，解決祖籍認同問題，恢復華族自信心，提高民族自豪感，進而自覺地擔當起華族優秀文化學習和傳承的重任，做一個名副其實的華人。

xjv：j時段用電量是否在第v檔范圍，若在值為1，否則值為0，v∈[2，V]；

yijk：機器i加工工件k時是否在j時段進行加工，若加工，值為1，否則值為0；

tijk：機器i加工工件k時在j時段加工時長，當=1時，值為pik，否則，說明機器i跨時段加工工件k，需根據工件開始加工時間Sik、所需加工時長Pik和所在時段j的上下限計算該時段內的加工時長。

本文采用連續時間建模，xjv與yijk為布爾變量，是為了便于確定加工時段用電量處于第幾檔電價和機器i加工工件k時在j時段的加工時間而引入的，因此，不考慮照明等日常用電，只考慮生產機器耗電，建立電力成本最小化的目標函數如下：

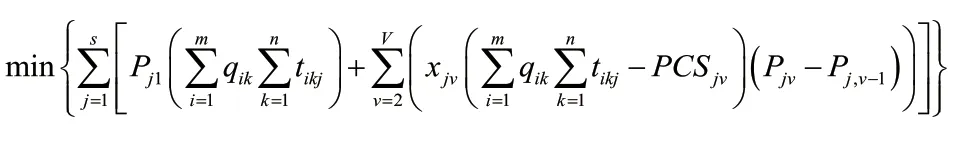
考慮約束條件如下：

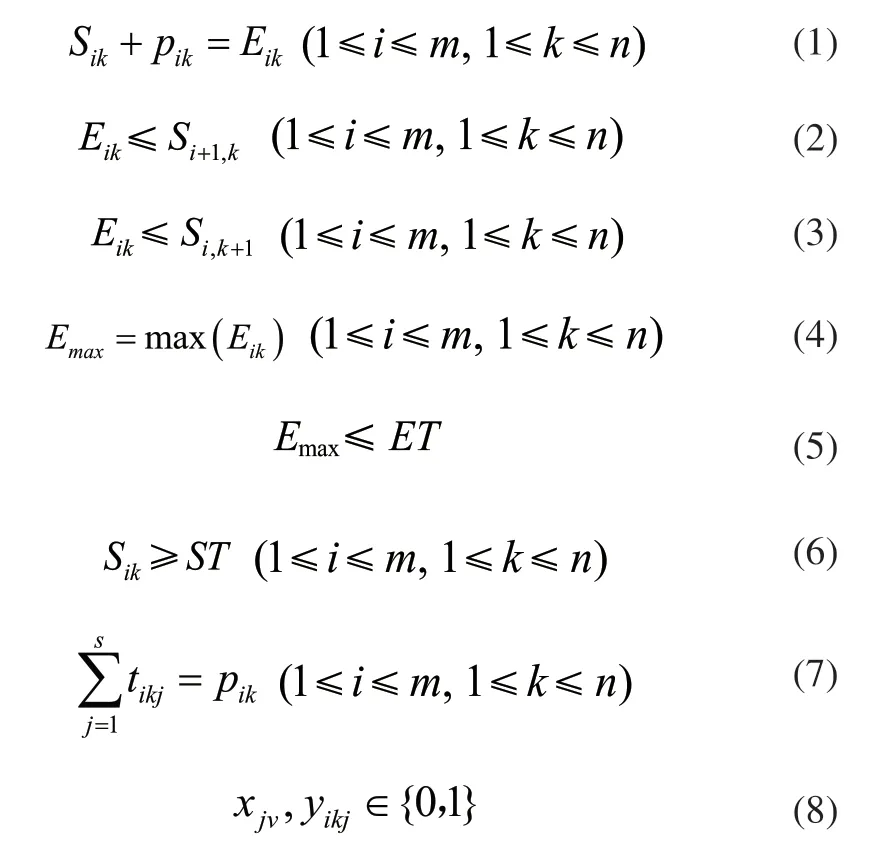
其中，（1）表示生產過程不被打斷，工件k在機器i上的開始時間加上加工時長等于結束時間，保證生產的連續性；（2）表示同一工件同一時刻不能在不同的機床上加工，每件工件k在當前機器i的結束加工時間小于在下一臺機器i+1的開始時間，同一工件的前道工序完成加工后才開始后一道工序；（3）表示同一時間一臺機器只能加工一個工件，每臺機器i加工當前工件k的結束時間小于加工下一件工件k+1的開始時間，同一臺機器加工完上一件工件后才能加工下一件工件；（4）、（5）、（6）、（7）表示要在規定時間內完成加工任務，開始加工時間和結束加工時間都必須在規劃時間內。

3 算法設計

考慮分時階梯電價的流水作業車間調度問題具有較高的復雜性，從流水作業車間生產調度的角度分析，需要考慮多個工件的加工順序，并計算各工件每道工序的開始加工時間和完工時間；考慮分時階梯電價后，不僅需要考慮加工順序，更需要在規定的時間范圍內針對各工件的開工時間進行合理的錯峰安排，才能最終確定各工件的開始加工時間，使得問題更加復雜。因此，針對該問題，本文采用具有強大全局尋優能力的遺傳算法進行求解。

3.1 編碼

考慮分時階梯電價的流水作業車間問題需要考慮工件的加工順序和作業開始時間，因此采用實數編碼，將整條染色體分為兩部分：工序碼+時間碼，第一部分是工序碼，基于工件的加工順序進行編碼，第二部分是時間碼，表示工件在每臺機器上的開始加工時間。

假設有4個代加工工件，每種工件有3道工序，對應的有3臺機器可以進行加工，設計一個可行解[3 3 3 2 2 2 1 1 1 4 4 4 | 0 5 11 5 11 18 6 13 21 7 15 24]，可行解分為兩部分，豎線前面的為工序碼，采取基于工序的編碼方式；豎線后面的為時間碼，表示與工序碼相對應的開始加工時間。本文編碼設計將工序碼和時間碼結合起來，工序碼確定工件的加工順序，時間碼確定機器開始加工時間，方便統計機器在某個時段內的加工時間和電力需求。

3.2 初始種群產生

圖2 染色體工序碼交叉操作

初始種群產生，在產生能在規定時間內的工序碼后，時間碼有兩種產生方式，前50%的種群采取完工時間盡可能短的方案，首件工件的首道工序從計劃開始時間加工；后50%的種群采取完工時間盡可能長的方案，末件工件的末道工序在計劃結束時間完工。兩種不同的時間碼產生方式，保證種群時間碼的多樣性。

3.3 交叉算子

交叉算子分為兩種，針對工序碼的交叉采用POX（precedence operation crossover）交叉算子，POX交叉算子可以很好的保留父代優良特征，繼承父代的加工順序，并且保證子代的可行性，如圖2所示；針對時間碼的交叉采用兩點交叉，隨機選中兩點，互換兩點之間的部分，時間碼交叉后可行性不易保證，因此采用后期修復的方法，保證子代的可行性。

3.4 變異算子

變異算子分為兩部分，第一部分對基于工序的工序碼變異，第二部分是針對時間碼變異，本文采用兩點互換操作，在相應部分任意選擇兩個互換點，然后互換對應位置的編碼，并對時間碼進行修復，此變異操作方法可以保證編碼的合法性。

3.5 選擇算子

選擇算子需要將本代種群中適應值較高的染色體保留到下一代以保證種群朝著更優的方向進化，本文編碼包含工序碼和時間碼，因此以目標函數電力成本的倒數作為適應度函數，采用輪盤賭法進行選擇，保證符合要求的染色體可以保留到下一代。

3.6 算法流程

因為編碼包含了基于工序的工序碼和工序開始加工時間的時間碼，因此算法分為兩部分，首先是工序碼的迭代，在工序碼能保證在規定時間內完成任務后，再對時間碼進行迭代，促使電力成本最低。因此，設計算法流程圖如圖3所示。

4 實例分析

圖3 算法流程圖

針對某考慮分時階梯電價的流水車間調度問題：某車橋加工車間共有6臺機器，現有4種工件，每種各5件，共20件工件需要加工，計劃從早上7點開始加工，要求40個小時內完成加工任務（包括一個低谷時段，四個平峰時段，四個高峰時段）。每種類型工件的加工時間和功率需求如表1所示。

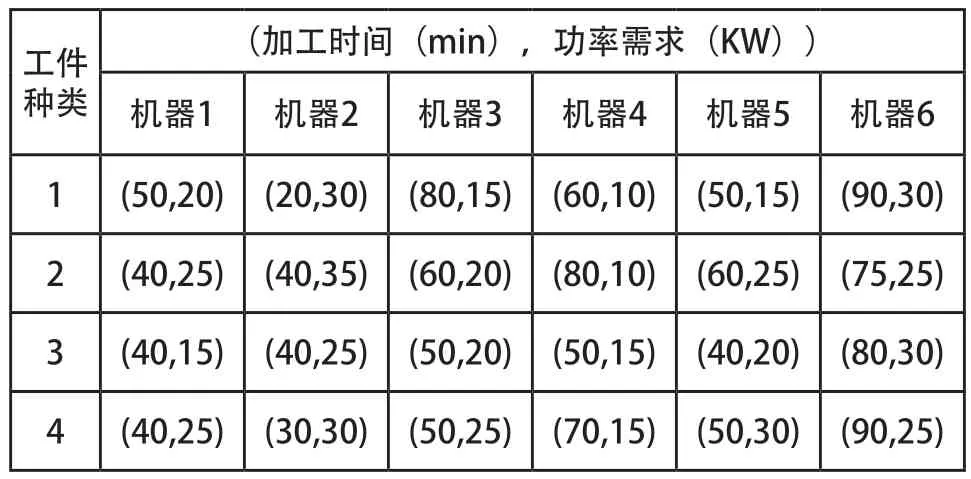
表1 各機器加工時間及功率

參考現行的陜西省分時電價和居民階梯電價，假設每個時段有兩檔電價，構建本文的分時階梯電價模型。第一檔為正常用電，第二檔為高標準用電，假設每時段電力價格如表2所示。

表2 分時階梯電價時段及價格表

分時階梯電價的分界點根據每天峰平谷三個時段的長度確定，取高峰段，平段，低谷時段用電量第二檔電價分界點分別為750千瓦時/天、850千瓦時/天、800千瓦時/天。

在考慮分時階梯電價下，本文以電力成本最小化為目標，設置種群規模為50，種群迭代次數為600，時間碼迭代次數為300。迭代10次得到最優調度方案甘特圖如圖4所示，同時以最小最大完工時間為目標作為對照組，得到最優調度方案甘特圖如圖5所示。對比兩組的電力成本如表3所示。

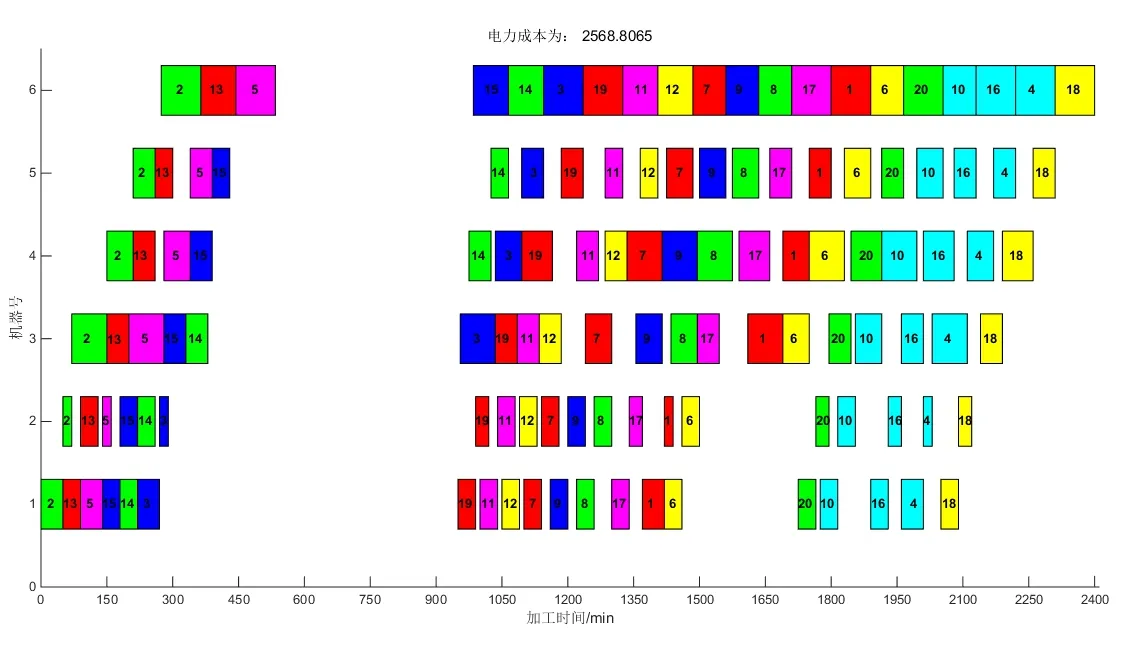
圖4 以電力成本最小化為目標的最優調度方案甘特圖

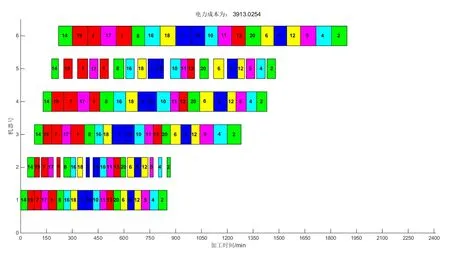
圖5 以最小最大完工時間為目標的最優調度方案甘特圖

表3 考慮不同目標的調度結果對比

從圖4中可以看出，考慮分時階梯電價的生產調度可以在規定的時間內完成加工任務并有效的進行錯峰生產，從表3的對比數據中可以看出，考慮分時階梯電價的情況下，以本文所建立出的模型，求解出的調度方案使得電力成本降低了34%，有效的降低生產所需的能耗。

5 結語

本文綜合考慮了分時電價和階梯電價，針對流水車間調度問題建立了數學模型，并針對建立的數學模型設計了基于工序編碼和時間編碼的遺傳算法，最后以實例驗證了該問題數學模型的正確性和求解算法的有效性。結果表明，在分時階梯電價下，以最小化電力成本為目標，進行生產調度決策，可以有效的進行錯峰生產，顯著的降低電力成本。本文只考慮了工件加工過程中的能耗，在未來的研究中，將考慮加入非加工過程產生的能耗，如等待能耗，開關機能耗等，進一步提高問題的實際意義。