基于改進粒子群算法的無人機路徑規劃*
王翼虎,王思明
(蘭州交通大學自動化與電氣工程學院,甘肅 蘭州 730070)
1 引言
近年來,無人機技術發展迅猛,路徑規劃問題是無人機自動控制的關鍵問題之一。目前路徑規劃的常用方法有粒子群PSO(Particle Swarm Optimization)算法、A*算法[1]、蟻群算法[2,3]、人工勢場法[4]等。粒子群算法應用于無人機路徑規劃時,易于實現且收斂速度快,但是由于其進行路徑規劃這類高維復雜問題的優化時極易出現早熟現象,這嚴重限制了算法的實際應用。
針對粒子群算法的問題,國內外學者進行了諸多嘗試。文獻[5,6]采用自適應原理調整參數,在算法的不同時期采用不同的慣性權重和學習因子,能夠在一定程度上改善粒子群算法的早熟收斂,但是對參數的選擇需要更多的數據實驗,同時參數對于環境規模的適應性不足,算法靈活性不高。文獻[7]提出一種自適應混沌粒子群優化算法并應用于三維路徑規劃,采用自適應logistic混沌映射優化全局最優粒子的方法引導種群跳出局部最優,該算法可以有效地使種群快速跳出局部極值點,但是對于算法總體尋優效率并沒有提升。文獻[8]提出一種基于粒子群優化和極坐標機器人路徑規劃方法,用概率論方法分析了該方法的收斂性,并分析了參數選擇對收斂性的影響,對于粒子群路徑規劃參數選擇具有一定指導意義,但是該方法本身規劃質量和效率并不高。文獻[9]在粒子群算法中引入模擬退火算法,使得種群能夠跳出局部極值點,提高了粒子群算法的全局尋優能力,但在局部搜索能力上仍存在局限性。
本文根據無人機路徑規劃任務建立三維高程環境模型,構造基于路徑長度、障礙危險以及高程代價的適應度函數。針對傳統PSO算法的缺陷,本文在傳統粒子群算法中引入BFO(Bacteria Foraging Optimization)算法的趨化算子和遷徙算子進行改進,提出了PSO-BFO混合算法,最后通過Matlab對2種算法進行三維全局路徑規劃仿真,驗證了改進算法的有效性。
2 無人機路徑規劃環境建模
本文研究在已知環境下的無人機的全局路徑規劃,建立模擬城市環境的三維高程數字地圖模型。考慮無人機飛行安全裕度后用圓柱體模擬建筑物,用半球體模擬其他樹木等障礙及禁飛區,其三維高程數學模型表示為[10]:
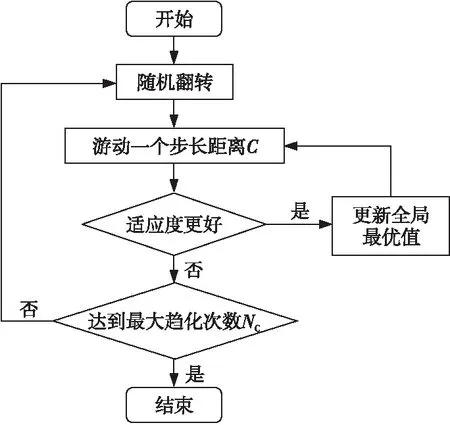
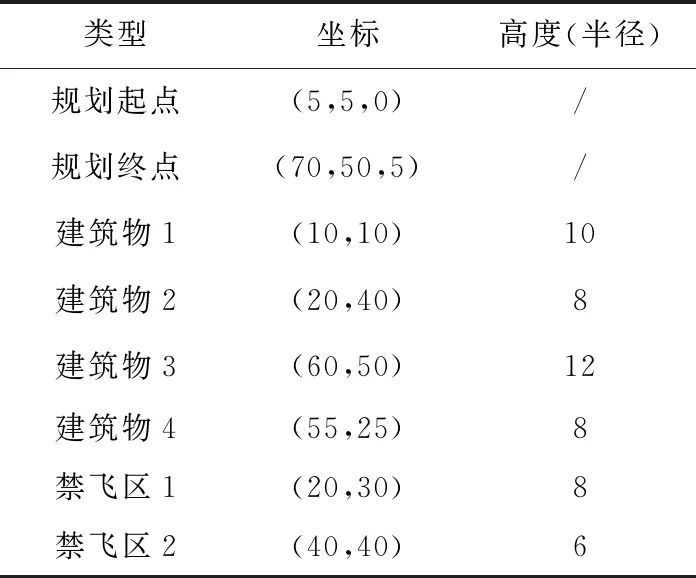
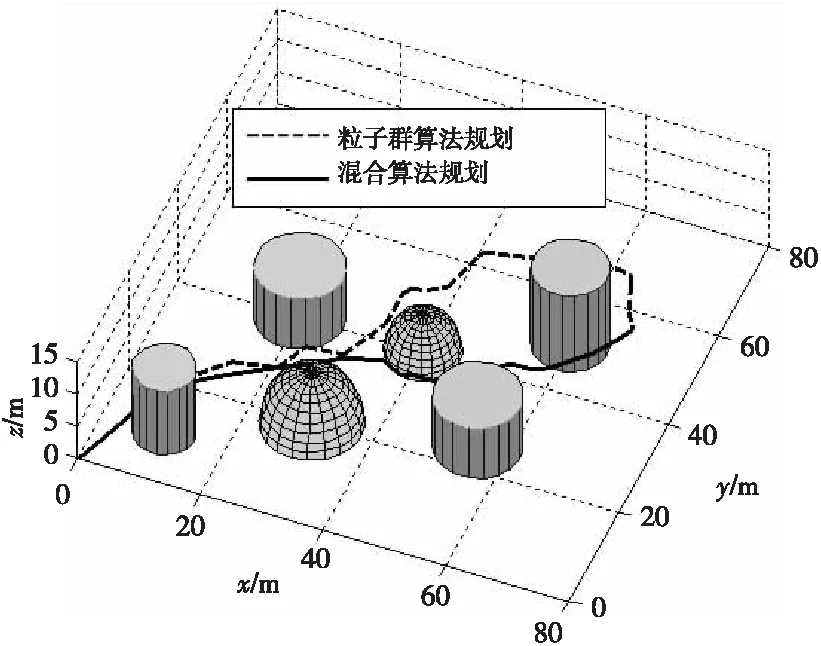
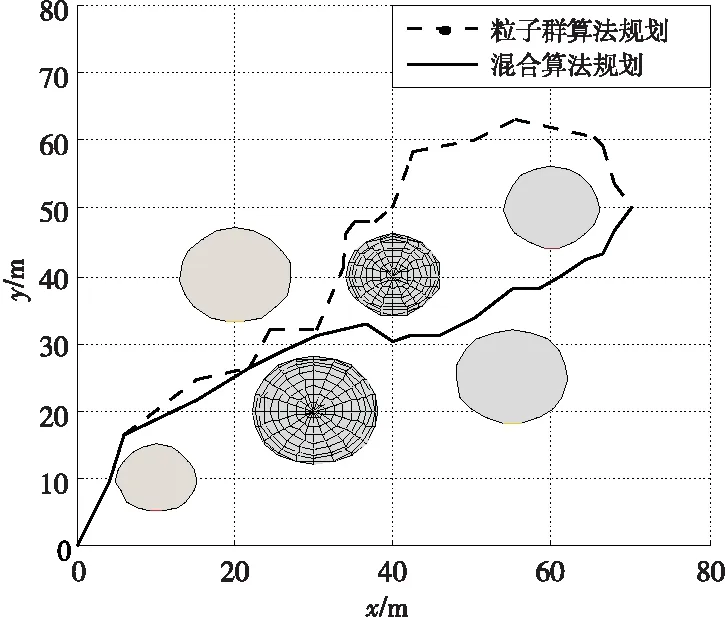
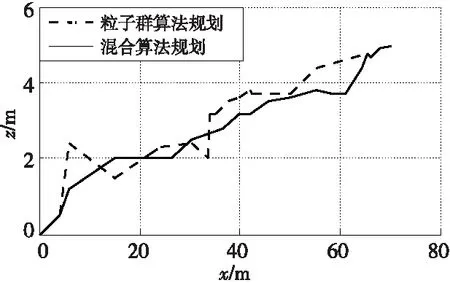
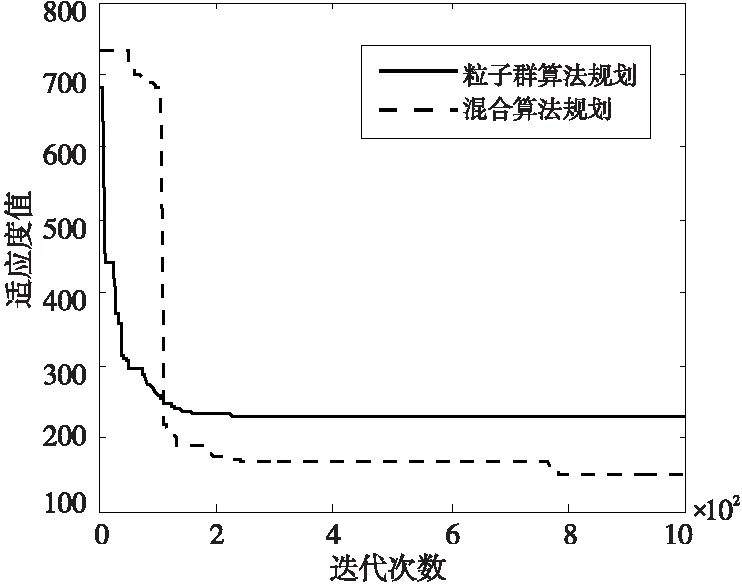
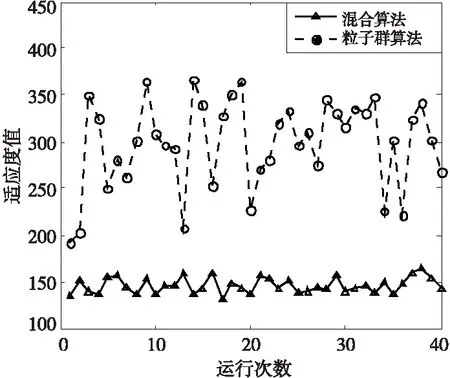
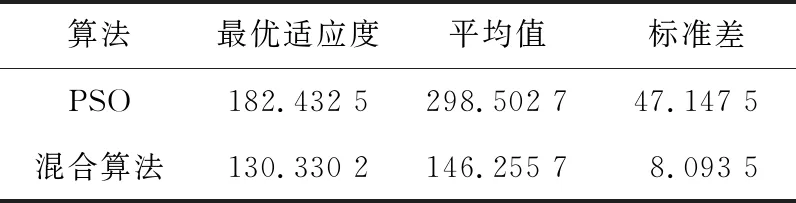
z1(x,y)=hi,r z(x,y)=max(z1(x,y),z2(x,y)) (1) 在采用粒子群算法進行路徑規劃時,適應度函數用以評價生成路徑的優劣程度,也是算法種群迭代進化的依據,適應度函數的優劣決定著算法執行的效率與質量。為了更好地進行路徑質量判斷,本文綜合考慮路徑的長度代價、障礙危險代價以及路徑平滑度幾個方面來構造適應度函數。假設有C條路徑,每條路徑由n個點組成,環境中共存在g個球形和柱形障礙。 路徑長度是評價路徑優劣最重要的指標之一,路徑越短,其耗時和耗能都越少。引入路徑長度代價如下: (2) 其中,Tm代表第m,m∈{1,2,…,M}條路徑中所有相鄰節點之間的距離總和,(xj,yj,zj)為路徑中第j個節點的坐標。 則第m條路徑的障礙威脅代價為: (3) 其中,rk為球形障礙或柱形障礙的半徑。 無人機的穩定飛行高度也是無人機航跡規劃過程中的重要環節。對于大多數飛行器來說,飛行高度不應該發生太大的變化。穩定飛行高度有助于減輕控制系統的負擔,節省更多的燃料。故引入航跡高程代價: (4) 高程代價為航跡每個相鄰航跡點高度差之和,其中hj表示路徑節點j的高度。 綜合Tm、danm和Cm得到路徑適應度函數為: f=w1·Tm+w2·danm+w3Cm (5) 其中,w1、w2和w3為[0,1]內的權重系數,用來靈活配置Tm、danm和Cm之間的關系。 粒子群算法用搜索空間中的點模擬自然鳥群中個體,將其覓食行為的過程類比為可行解變換優化的迭代過程。其搜索過程基本不利用外部信息,僅以適應度函數作為進化依據,每個個體根據個體極值和全局極值接近最優解。本文以粒子群算法為基礎進行迭代尋優,并且引入細菌覓食算法對粒子群算法進行改進。 假設存在一個規模為M的粒子種群,具有N維空間搜索區域,記為X=[x1,…,xi,…,xM]T,其中第i個粒子的位置表示為xi=[xi1,xi2,…,xiN]T,其速度即粒子在每次迭代中移動的距離表示為vi=[vi1,vi2,…,viN]T,粒子i當前經過的適應度最佳的位置即個體極值表示為Pi=[pi1,pi2,…,piN]T,用Pg=[pg1,pg2,…,pgN]T表示整個種群搜索到的適應度最佳的位置即全局極值。優化問題的可行解即為優化粒子的位置。粒子每次迭代按式(6)更新其位置與速度[11]。 (6) 細菌覓食算法BFO是群體智能算法的一種,模擬細菌種群覓食行為進行建模,通過迭代來產生最優解。在BFO算法中,算法尋優由趨化、繁殖和遷移3個操作的三層嵌套循環構成,最內層是趨化,中間層是繁殖,最外層是遷移,下面對以上操作分別做簡要介紹[12]。 (1)趨化操作。 細菌趨化算子的操作描述為:細菌首先向隨機方向游走一個步長單位的距離,如式(7)所示;然后計算該位置適應度,如果新位置的適應度優于上一個位置的,則沿翻轉方向再前進單位步長,若適應度劣于該細菌所在上一個位置的,或者達到最大游動次數則退出該次趨化操作。 P(i,j+1,k,l)=P(i,j,k,l)+C(i)φ(i) (7) 其中,P(i,j+1,k,l)為細菌位置,i為細菌的序號,j,k,l分別為趨化、復制、遷徙操作次數,C(i)為細菌執行一次趨化操作向前游動的單位步長,φ(i)表示細菌隨機翻轉中生成的隨機單位方向向量。 (2)繁殖操作。 在細菌完成一定次數的趨化過程后,進行繁殖操作,定義細菌的繁殖能量為細菌在整個趨化過程內的適應度之和,高繁殖能量的細菌獲得繁殖機會,低繁殖能量的則被淘汰。 設淘汰掉的細菌數量為Sr=S/2,將細菌按照繁殖能量高低排序,然后淘汰低能量的Sr個細菌,剩余細菌進行自我復制分裂出與自己完全相同的新個體,取代被淘汰的個體,保持細菌種群大小不變。 (3)遷徙操作。 完成種群的繁殖操作后,細菌個體以一個固定概率Ped進行遷移,對任何細菌個體隨機生成一個[0,1]的隨機數Rand。若Rand 粒子群算法早期搜索速度較快,但同時也帶來一個問題,粒子搜索過程中PSO算法會因為粒子速度過大而錯過最優解[13],而且由于所有粒子在“跟隨”思想的引導下,都向著一個方向飛行,導致粒子趨向同一化,喪失種群多樣性,導致算法陷入局部最優,且算法在后期缺乏跳出局部最優的能力。 針對以上問題,本文在粒子群算法中引入BFO的趨化和遷徙算子。BFO算法的趨化過程實質就是細菌在解空間中搜索其所在位置的鄰域,由適應度函數決定其搜索方向。趨化過程的引入將增強PSO的局部搜索能力,改善PSO中粒子在搜索過程中由于速度過大而錯過最優解區域的問題。而引入遷徙算子會在粒子群陷入局部最優時使得算法有跳出局部最優的能力,將有利于算法跳出局部最優,但是固定概率的遷移算子會使部分優秀解流失,降低尋優速度,故將粒子按照適應度排序,只賦予低適應度的粒子遷移概率Ped。 PSO-BFO算法的具體步驟如下所示: (1)初始化環境信息,確定規劃空間邊界為R=(xmax-xmin,ymax-ymin,zmax-zmin),提取起始點S(xstart,ystart,zstart),目標點G(xend,yend,zend)。 (2)設置種群大小pop_size及粒子大小part_size,最大迭代次數max_gen,粒子最大速度vmax=0.1R,初始化粒子的位置和速度如式(8)和式(9)所示。 (8) (9) (3)計算粒子初始適應度值f0,將粒子當前位置設為個體極值pbest0,將所有粒子中適應度最好的粒子位置設為全局極值gbest0,設置慣性權重wmax,wmin和學習因子c1,c2,迭代次數計數k=1。 (4)根據w=wmax-(wmax-wmin)(k/max_gen)線性遞減策略更新慣性權重,根據式(6)更新粒子的速度和位置,計算個體適應度值fk,如果獲得更優的個體極值和全局極值,則更新個體極值pbestk和全局極值gbestk。在全局極值獲得更新時,加入趨化算子進行局部尋優,局部尋優流程如圖1所示。 σ2計算方法如下所示: (10) Figure 1 Flow chart of chemotaxis operator圖1 趨化算子流程圖 (6)判斷是否滿足停止計算條件或達到最大迭代次數,是則輸出規劃結果;否則返回步驟(4)且k=k+1。 實驗在三維高程地圖模型下,分別用PSO算法與PSO-BFO混合算法進行無人機路徑規劃仿真。實驗所用電腦配置為Windows 7 64位系統,8 GB運行內存,2.5 GHz頻率CPU,程序在Matlab平臺運行。路徑起終點以及規劃環境參數設置如表1所示,粒子群算法參數設置如表2所示,混合算法中粒子群算法參數不變,加入細菌覓食算子,游動步長C=0.05|R|,最大趨化次數Nc=30,遷移概率Ped=0.25。 Table 1 Parameter settings for planning tasks 表1 規劃任務參數設置 Table 2 Parameter setting of particle swarm algorithm表2 粒子群算法參數設置 為驗證混合算法在三維路徑規劃中的有效性,將PSO-BFO混合算法與基本粒子群算法在相同的環境模型中進行對比實驗。 圖2~圖4給出基本粒子群算法和本文混合算法的規劃結果及其俯視圖和正視圖,圖5給出了2種算法的最優適應度曲線。從圖2可以看出,傳統PSO算法和混合算法均能在三維環境中生成一條可行的全局路徑,但是由圖3和圖4可以看出,本文混合算法規劃結果的路徑長度和平滑度都要優于傳統PSO算法的,且由圖5最優適應度曲線可以看出,混合算法由于引入趨化算子增強了其局部尋優能力,避免其跳過全局最優解,加快了收斂速度,適應度呈直線下降,適應度優于傳統粒子群算法,且由于遷徙算子的引入使得算法陷入局部最優而停滯時也能夠跳出局部最優,恢復尋優能力。 Figure 2 Path planning results of PSO algorithm and hybrid algorithm圖2 粒子群算法和混合算法路徑規劃結果 Figure 3 Top view of planning results of PSO algorithm and hybrid algorithm圖3 粒子群算法和混合算法規劃結果俯視圖 Figure 4 Front view of planning results of PSO algorithm and hybrid algorithm圖4 粒子群算法和混合算法規劃結果正視圖 圖6給出2種算法重復40次運行的適應度值,表3總結了重復實驗中2種算法獲得的最優適應度,以及多次運行的適應度平均值及其標準差。從圖6及表3可以看出,傳統PSO算法在進行路徑規劃時,規劃路徑適應度最優值及平均值均較差,且在重復運行中,規劃結果的標準差遠大于改進算法的,規劃的穩定性差,這也使得其很難實際應用。而混合算法的多次運行結果最優值、平均值和標準差均大幅優于傳統PSO算法的,說明混合算法不但增強了算法尋優能力,而且算法的穩定性也得到很大的提升。 Figure 5 Optimal fitness curves of PSO algorithm and hybrid algorithm圖5 粒子群算法和混合算法最優適應度曲線 Figure 6 Simulation results of algorithms running for many times圖6 算法多次運行仿真結果 表4給出了算法多次運行時的平均迭代總耗時Alltime(迭代次數達到設定的最大次數的時間)、算法收斂時的迭代次數Iter(最優適應度連續100代未更新)以及耗時Time,表中數值均為平均值。由表4可以看出,從算法總耗時上看,混合算法由于引入了趨化和遷徙算子,增加了一定的計算量,所以總耗時要高于傳統PSO算法的,但是從算 Table 3 Simulation data comparison of PSO algorithm and hybrid algorithm 表3 PSO算法與混合算法仿真數據對比 法收斂時間上看,混合算法從開始到收斂的迭代次數平均值要比傳統PSO算法低112.3,耗時也相應更短,這說明混合算法雖然增加了一定計算量,但是加快了算法收斂速度,整體效率優于傳統PSO算法。 Table 4 Efficiency comparison of PSO algorithm and hybrid algorithm表4 PSO算法和混合算法效率對比 在無人機的三維路徑規劃問題中,傳統PSO算法的尋優能力無法滿足需求,本文將BFO算法的趨化算子和遷徙算子引入PSO算法提高了其尋優能力。最后分別對PSO算法和改進后的混合算法進行無人機路徑規劃仿真并對結果進行對比分析。仿真結果表明:與傳統PSO算法相比,混合算法在路徑規劃問題中,尋優結果最優值與平均值均大幅優于傳統PSO算法的,且多次運行時結果穩定性良好,在無人機的全局路徑規劃中具有一定的參考性與實用性。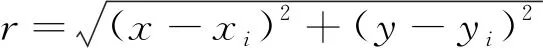
3 適應度函數
3.1 路徑長度代價
3.2 障礙危險代價
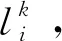
3.3 航跡高程代價
4 改進粒子群算法
4.1 粒子群算法

4.2 細菌覓食算法
4.3 PSO-BFO混合算法

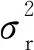

5 實驗分析


6 結束語

