繩牽連物體的運動研究

王維國

(江蘇省海安高級中學，江蘇 海安 226600)

繩桿關聯系統是力學中的經典問題，對中學生來說是一個難點，在高考中屢見不鮮，也引起了一些研究者的關注．在研究繩桿關聯系統速度和加速度關系時，不少人利用運動的合成與分解規律分析，或在直角坐標、自然坐標、極坐標下，用高等數學方法對幾何關系式、速度關系式求導.[1]有研究者指出轉動的繩牽連兩物體的速度并非同時達到最大，并計算了速度最大的位置.[2]有人用幾何畫板、MATLAB作出了繩桿兩端物體的加速度等物理量隨角度變化的圖像.[3，4]有的文獻提及可用數值求解拉氏方程得到速度加速度和張力隨時間變化，但沒有詳述．[5]而對繩牽連物體的運動量隨時間變化規律定量關系的研究卻未見到.本文對此及相關問題進行系統的分析，并將結論用圖像進行直觀呈現．

1 問題的由來

以某市2020屆高三第一次調研試卷中的一道選擇題為例.

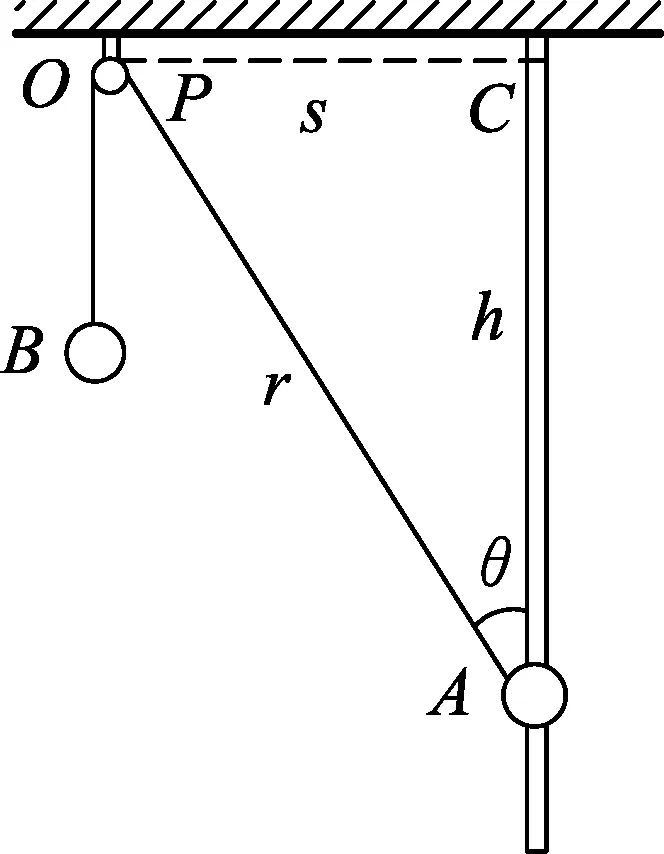
圖1

例1.如圖1所示，豎直桿上套有一個質量為m的小球A，用不可伸長的輕質細線通過輕質小定滑輪O，連接小球A、B．小球A從細繩與豎直方向的夾角為37°的位置由靜止釋放，恰能運動到細繩與豎直方向垂直的C點，一切阻力不計，已知sin37°=0.6.則

(A) 小球A在上升過程中加速度先減小后增大.

(B) 小球B在最低點時加速度和速度都為0.

(C) 小球B的質量為1.25m.

(D) 小球B的質量為2m.

答案： (A)、(B)、(D)．

不少教師對選項(B)有疑問，認為小球B從最高點開始運動先加速后減速，在最低點速度為0，而后向上做往復運動，所以在最低點時小球B加速度應該向上，而不為0．

本文就這個繩牽連物體問題從多個角度進行定量分析．

2 牽連加速度關系

因為張緊的剛性繩的總長度不變，所以兩端物體沿繩方向的速度大小相等．有學生據此進行知識遷移，認為沿繩方向的加速度大小也相等．這個結論能否成立，需經推理證明．

2.1 繩牽連加速度關系的推導

我們用兩種方法分析兩小球在任意位置加速度aA、aB大小的關系．

2.1.1 相對運動法

取與輕小滑輪相切右側繩上的點為P點，設P點到豎直桿的距離為s，繩與豎直方向的夾角為θ．任意時刻A球相對P點做圓周運動，有切向加速度aτ和向心加速度an，則A球相對動點P的加速度aAP有

aAP=aτ+an.

(1)

A球和繩上P點相對地面的加速度分別為aA、aP，由相對運動加速度關系有

aA=aAP+aP.

(2)

設B球的加速度方向向下，則繩上P點的加速度沿滑輪切向(AP方向)，與B球的加速度大小相等，aB=aP．

將(1)式代入(2)式，把(2)式投影到繩AP方向，得A球在AP方向上的加速度

aAcosθ=an+aB，

(3)

其中向心加速度為

(4)

將(4)式代入(3)式得任意位置兩球加速度大小關系

(5)

此式中，A球加速度向上為正方向，B球加速度向下為正方向．

2.1.2 對幾何關系式求導

在一些文獻中，研究加速度關系用高等數學方法時涉及到單位矢量的導數，較為繁瑣．如果在描述幾何關系時，避免用角度參量，就能使運算過程更為簡單．

設A球到P點距離為r，A球到C點距離為h，由幾何關系得

r2=s2+h2.

(6)

將(6)式兩邊對時間求導得

(7)

因為r、h均隨時間減小，所有

(8)

將(8)式代入(7)式得

rvB=hvA.

(9)

將(9)式兩邊對時間求導得

(10)

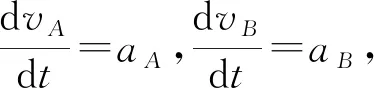
-vB2+raB=-vA2+haA.

即

(11)

(12)

(12)式與上一節所講的結果(5)式相同．

2.2 牽連加速度關系討論

在零時刻，A球在最低點，B球在最高點，vA=0，vB=0，則aAcosθ=aB；當A球運動到最高點，B球最低點，vA=0，vB=0，仍滿足aAcosθ=aB．在這兩個位置，“沿繩方向的加速度大小相等”是成立的，其條件是繩沒有轉動．B球最低點時，A球運動到最高點，繩水平，A球的加速度aA=g，且cosθ=0，則aB=aAcosθ=gcosθ=0.上述試題中的(B)選項“小球B在最低點時加速度和速度都為0”是正確的．在繩兩端的物體的速度均為0時，繩的角速度為0，因此就沒有向心加速度，此時兩端物體沿繩方向的加速度相等．而很多人想當然地認為“B球在最低點會向上運動，所以加速度方向應向上”，其實在往返運動中，速度等于0時，加速度是可以同時為0的．

3 兩球會同時達到最大速度嗎？

兩球速度都從0起先增大到極大值，然后減小到0，做往復運動.有人認為兩球速度會同時達到極大，下面就這個問題進行定量分析．

3.1 兩球達到最大速度的先后問題分析

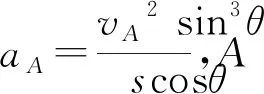
3.2 兩球速度變化過程的圖像分析

初始位置繩與豎直方向的夾角為θ0=37°，根據機械能守恒定律

(13)

得

mB=2mA=2m.

(14)

A從最低點運動到任意位置的過程中

(15)

vB=vAcosθ.

(16)

解得

(17)

(18)

將上式進行無量綱化處理，得

(19)

(20)

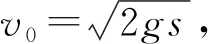
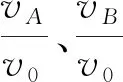
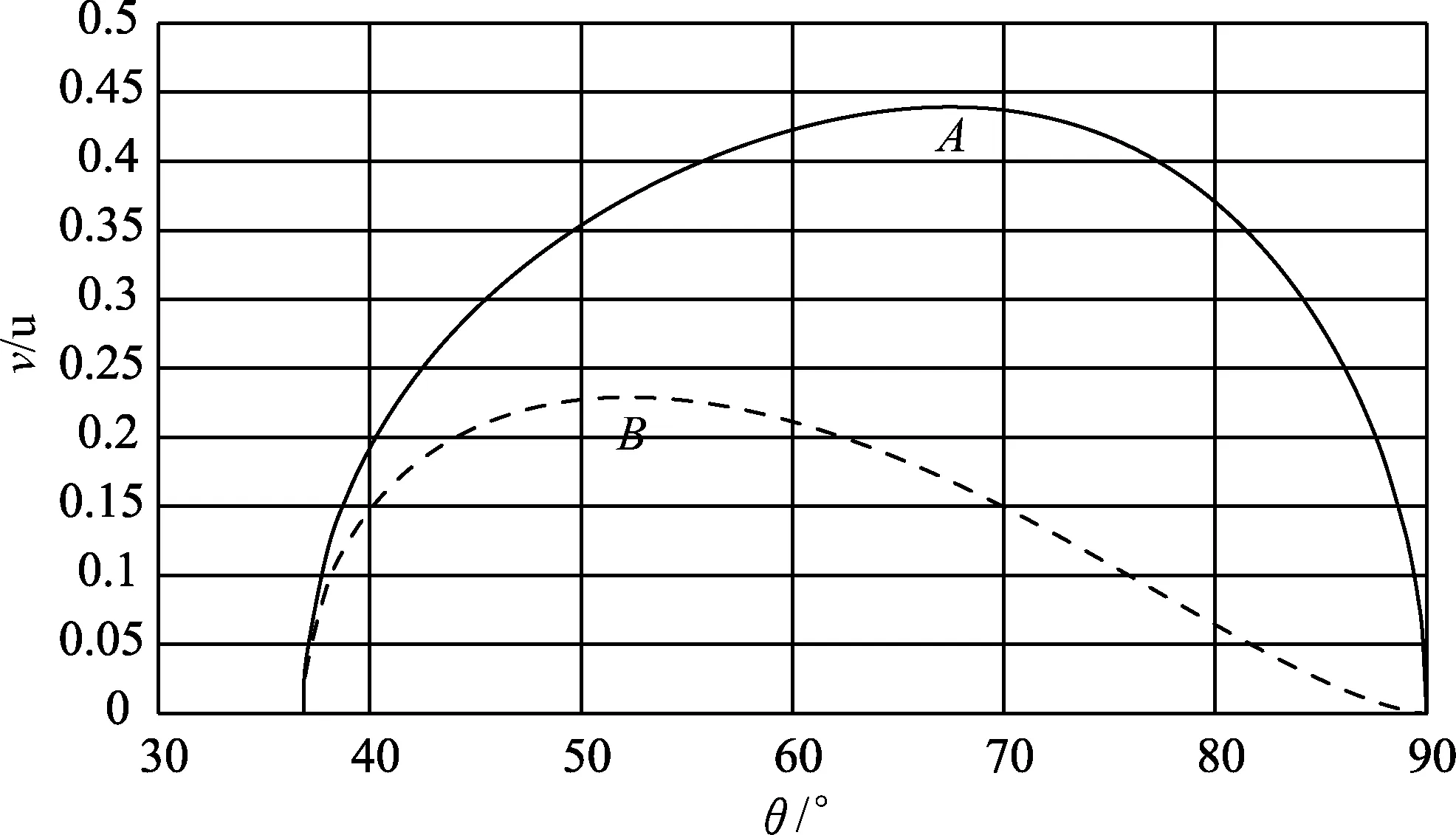
圖2 速度隨角度變化

從圖2可知，在A球上升B球下降過程中，θ從37°增大到90°,當θ=52°時，B球的速度先達到極大值，θ=67°，A球的速度后達到極大值．用Excel的數值計算功能可得A、B兩球速度先達到極大值的角度分別為52.2°和67.5°．在A球下降B球上升過程中，θ從90°減小到37°,A球的速度先達到極大值，B球的速度后達到極大值．

3.3 加速度隨位置的變化情況

根據牛頓第二定律，有

Tcosθ-mg=maA.

(21)

2mg-T=2maB.

(22)

根據(12)、(17)-(22)式解得

(23)

(24)

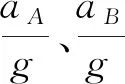
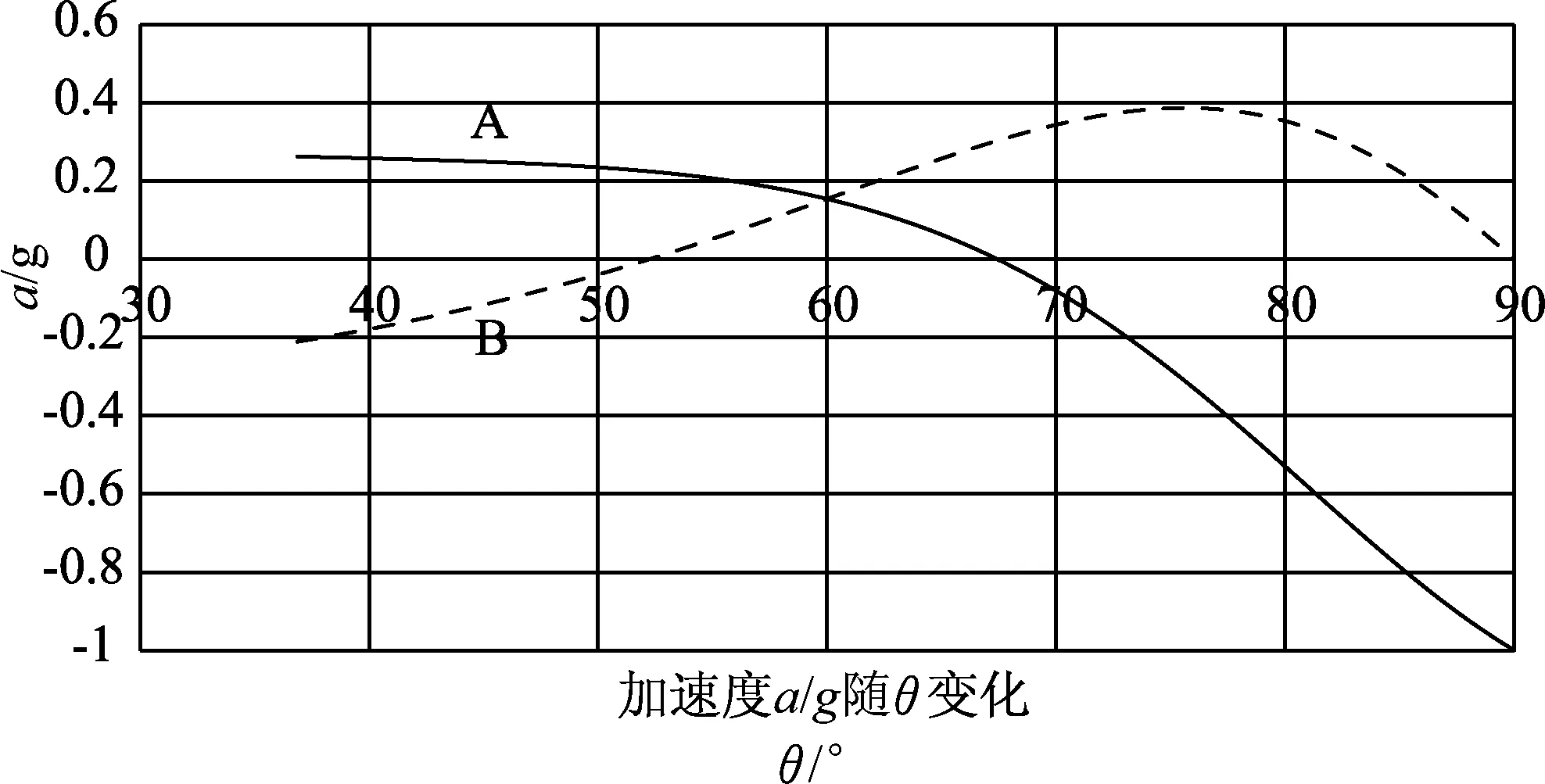
圖3 加速度隨角度變化

從圖3可知，當θ=52°時，aB=0，B球的速度達到極大值，θ=67°時，aA=0，A球的速度達到極大值，與圖2中位置一致．當θ=90°時，A球在最高點，vA=0，aA=g，B球在最低點，vB=0，aB=0，即B球的速度與加速度同時為0．

3.4 速度與加速度隨時間的變化規律

由牽連加速度關系式寫成微分方程，不易得到解析解．采用MATLAB程序，可以作出兩球運動的速度隨時間變化的圖像．

由理論力學規律可知保守系的拉格朗日函數：[7]

L=T-V，

(25)

其中L代表體系的動能與勢能之差，體系的動能為

(26)

(27)

拉格朗日量中勢能的零勢面對解沒有影響.為方便表述，取A球的勢能在C點時為0，B球的零勢能面取B球運動的最低點下方s處，則體系的勢能為

(28)

將(26)-(28)式代入(25)式得拉格朗日量為

(29)

保守力系的拉格朗日方程為

(30)

令廣義坐標q(t)=θ，則廣義速度q′(t)=ω，

(31)

(32)

最終方程為

(33)

化簡后用MATLAB程序求解得到θ和ω，再代入下式中的速度關系．

(34)

設s=1 m，得到速率v隨時間t變化圖像，如圖4所示圖線A,B分別指vA,vB．

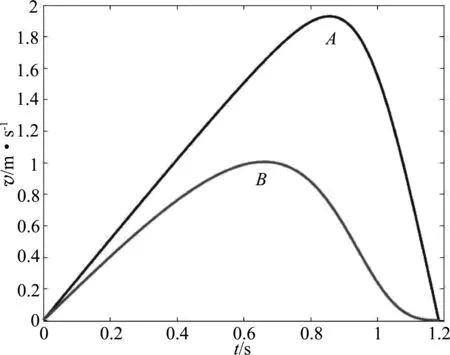
圖4 v-t圖像

從圖4可以看出，在B球下降過程中，速度從極大值減小到0的過程中圖像中存在一個拐點，加速度先從0起增大后減小到0，在B球速度為0時速率圖線的切線的斜率為0，從另一個角度印證了選項(B)是正確的．

從圖5可以看出，在B球下降過程中，加速度大小在兩個時刻為0，一是速度為極大值時，另一個是速度減小到0時．

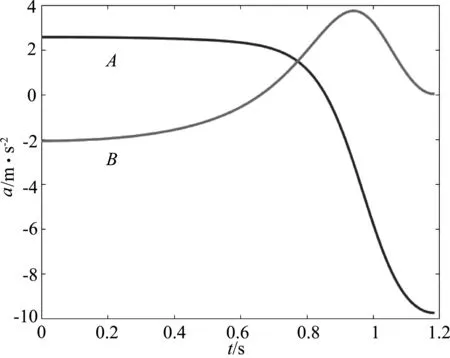
a-t圖

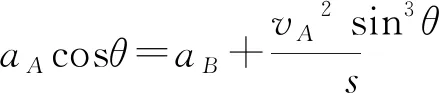
4 教學與命題建議

繩桿關聯系統問題，常見諸高考試卷，如2018年高考江蘇卷第15題.

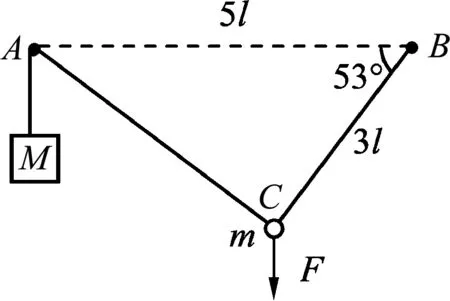
圖6

例2.如圖6所示，釘子A、B相距5l，處于同一高度．細線的一端系有質量為M的小物塊，另一端繞過A固定于B．質量為m的小球固定在細線上C點，B、C間的線長為3l．用手豎直向下拉住小球，使小球和物塊都靜止，此時BC與水平方向的夾角為53°．松手后，小球運動到與A、B相同高度時的速度恰好為0，然后向下運動．忽略一切摩擦，重力加速度為g，取sin53°=0.8，cos53°=0.6．求：

(1) 小球受到手的拉力大小F；

(2) 物塊和小球的質量之比M:m；

(3) 小球向下運動到最低點時，物塊M所受的拉力大小T．

在第(3)問中，必須用到在此位置沿繩方向加速度大小相等的結論，分析CA方向的小球受力，列出牛頓第二定律表達式T-mgcos53°=ma，才能求出物塊所受的拉力．

小球在繞B點做圓周運動的過程中，相對與釘子A接觸的繩上的A1點做圓周運動，小球相對A1點有切向和向心加速度，只有在最高點和最低點，小球的速度為0，相對A1點的向心加速度為0，沿繩方向的加速度相等．在教學中，如果不強調這個加速度關系成立的條件，直接使用這個結論，會讓學生誤認為在任何情況下沿繩方向的加速度都相等．在高考命題中應盡量避免考查繩桿模型的加速度關系，可考查其中的力和能量問題．

在教學中為了打破“沿繩方向的加速度相等”這個思維定勢，可以通過分析一些實例來糾錯，單擺模型就是一個很好的例子，固定的懸點沒有加速度，在擺球運動過程中除了在最高點外都有向心加速度，所以沿繩方向加速度不一定相等．

5 結束語

本文通過分析一個繩牽連模型實例，闡述了繩轉動時牽連物體的速度、加速度隨位置、時間變化的規律，形象展現了相關物理量變化的圖景，有助于糾正“沿繩方向的加速度都相等”、“往返運動中速度為0時一定有加速度”等錯誤認知．理論需要實驗的檢驗，期待有研究者能減小摩擦阻力設計繩牽連模型的實驗，利用Tracker等影像追蹤分析軟件研究實際運動規律，與理論分析結論進行印證．