拓展教學思路 促進深度學習
——以一道經典力學題的拓展教學為例
陳志軍
(安徽省績溪中學,安徽 宣城 245300)
深度學習具有促進知識建構、著意遷移運用、面向問題解決的基本特征和思維層次,追求有效的學習遷移和真實問題的解決.[1]深度學習是落實物理學科核心素養的重要途徑,引導學生積極參與、體驗探究學習過程,掌握學科的核心知識,把握學科的本質及思想方法.[2]應用遷移、拓展探究則是構建思維型課堂的基本方法,是深度教學的主要特征,教學過程突出知識的形成過程、思維品質的訓練,著重發展學生高階思維和實際問題解決能力.[1]本文以一道經典力學題的拓展教學為例,著眼于知識的遷移應用和思維的發散,著力解決實際問題,促進學生深度學習,落實物理核心素養教學目標.
1 一道經典力學題
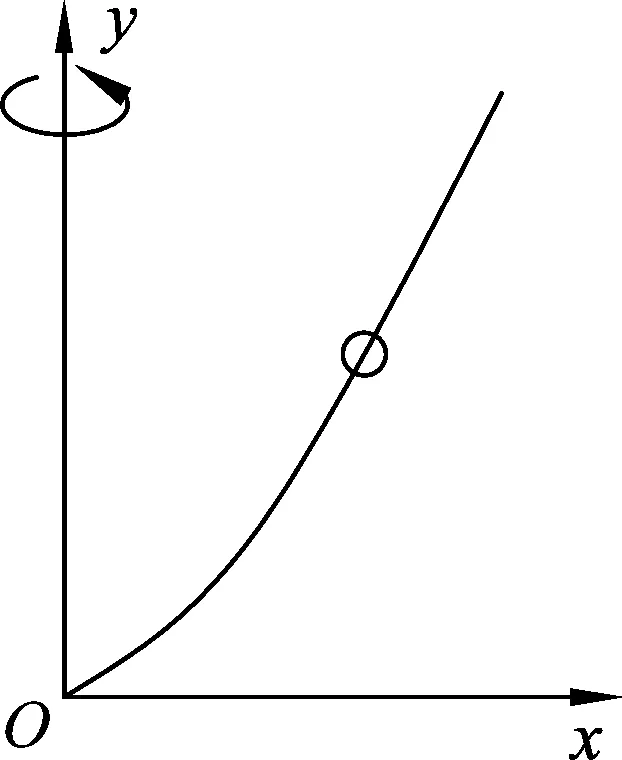
圖1
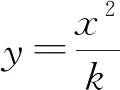
2 拓展探究教學分析
2.1 彎桿上任意點的斜率
(1) 利用極限法.
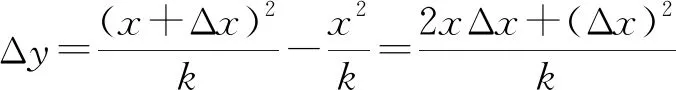
(2) 利用微分思想.

(3) 利用平拋運動的規律.
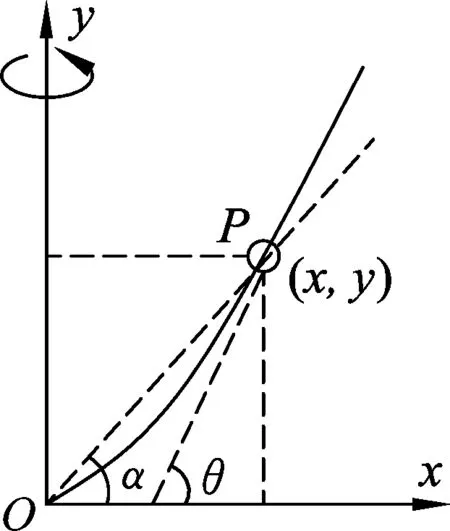
圖2
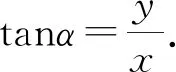
2.2 環的運動性質與規律
(1) 環在何處相對桿靜止.
(2) 環運動的性質和模型分析.

圖3
環運動的性質是水平面內的勻速圓周運動,所受重力和支持力提供向心力.教學中設計探究活動深入分析,將支持力方向延長交y軸于A點,探究確定環的運動符合“無繩”圓錐擺運動模型,如圖3所示,A點為圓錐擺的懸掛點,擺角為θ,AP為擺線,其軌跡在水平面內的一種典型的勻速圓周運動.題目并沒有給出擺角,要引導學生探究擺角的確定方法并求曲線的斜率,學生討論,教師指導,共同分析、評價、探討.圓錐擺運動模型是一種典型的力學模型,涉及到運動、力、能量等物理觀念.而日常生活中經常會遇到一些圓周運動,本質是圓錐擺,只是少了擺線,教學中引導學生通過與實際生活聯系,探究發現這些“無繩”的圓錐擺,分析該狀態下物體受力的特點、運動的規律,能很好地培養學生科學探究能力、科學思維能力、科學態度與責任和解決實際問題的能力,形成和發展物理觀念,指向物理學科核心素養的培養.[3]
(3) 逆向探究彎桿的曲線方程.
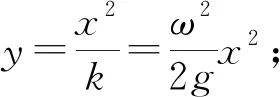
(4) 不同轉速下的彎桿約束的運動.
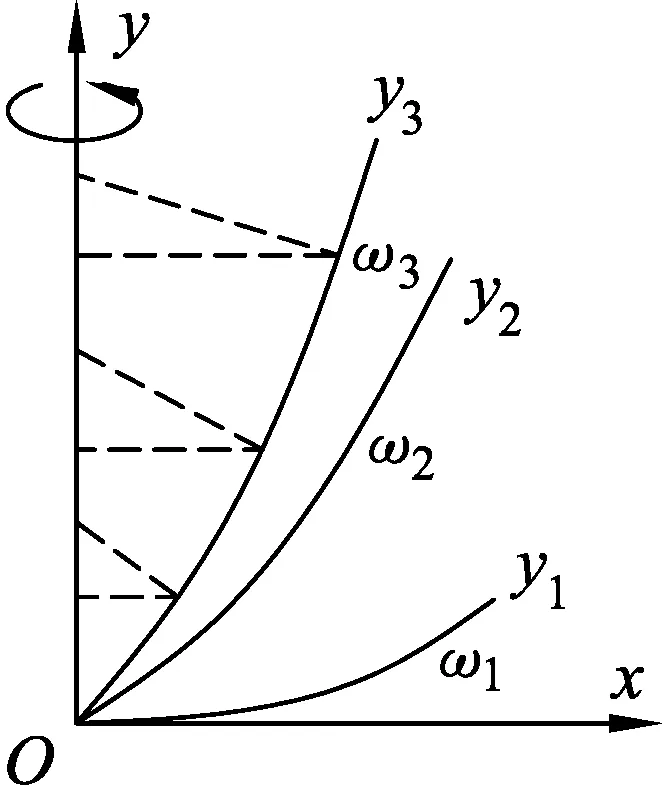
圖4
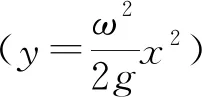
2.3 引入非慣性系,確定相對靜止的位置
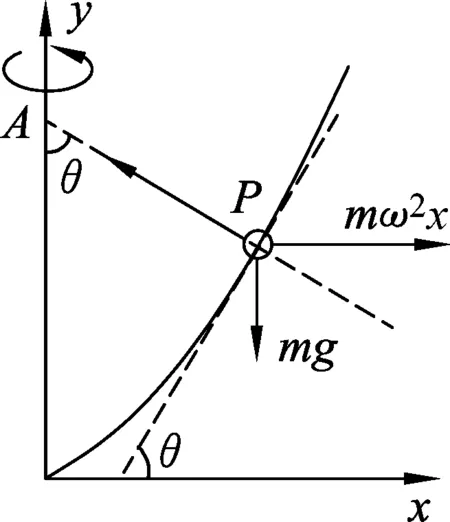
圖5
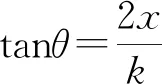
2.4 與直桿約束的圓周運動對比分析
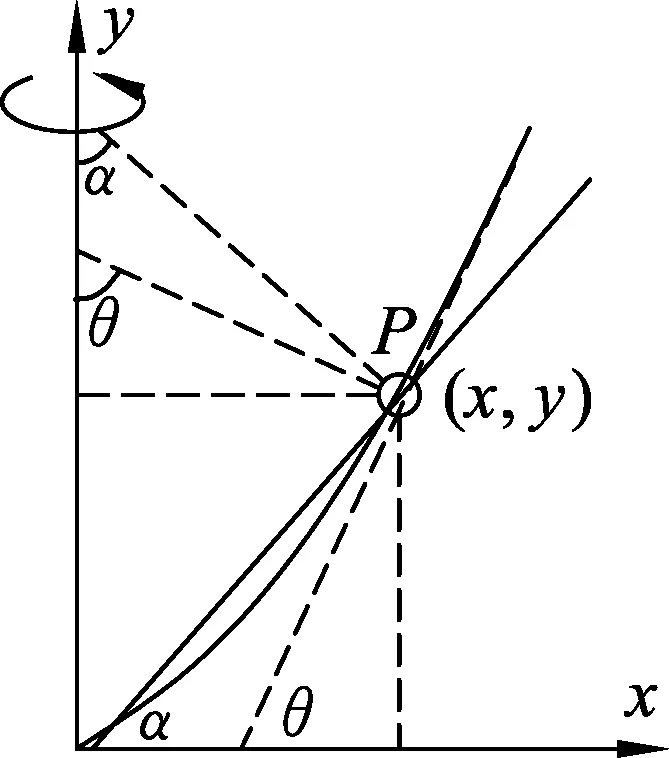
圖6
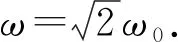
2.5 與圓形軌道約束的圓周運動對比分析
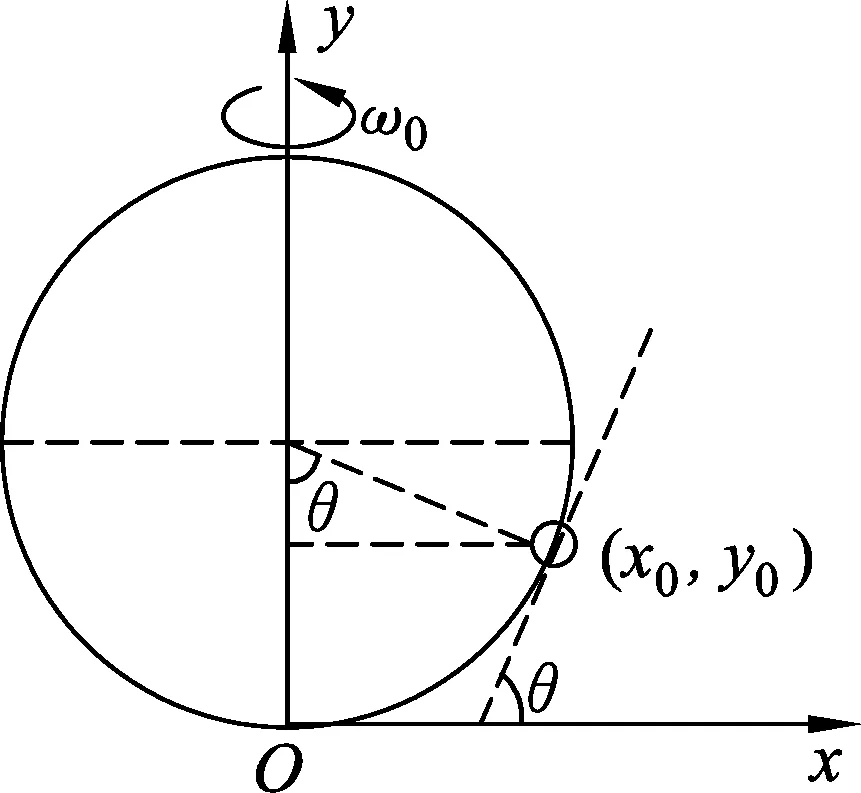
圖7
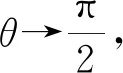
如圖7所示,光滑圓形桿的半徑為R,環可以隨圓形桿一起勻速轉動.根據圓的性質和坐標系中的位置,可以確定該圓的軌跡方程為x2+(y-R)2=R2.假設環在坐標為(x0,y0)的任意位置P點處以角速度ω0隨圓形桿一起做水平面內的勻速圓周運動,很明顯該運動在本質上仍然是圓錐擺運動.該點的切線對應的角度θ即為擺角,利用微分求導可以確定該點切線的斜率為
(1)
又根據環做勻速圓周運動的動力學方程知
mgtanθ=mω02x0=mω02·Rsinθ.
(2)
聯立(1)、(2)式可解得
(3)
(4)
(5)
從上述分析可以看出,直桿、特定形狀的拋物線桿、圓形桿都可以帶動圓環做“無繩”圓錐擺運動,直桿的情況下環的位置和角速度有一一對應關系;環可以隨特定形狀的拋物線桿在任意位置做水平面內的勻速圓周運動;而圓形桿的角速度必須要超過一個臨界值,才能使環運動起來.
3 結語
本題模型涉及物理學科核心素養,促進深度學習的探究點比較多.教學中要針對性拓展探究曲線切線斜率、支持力的大小及方向、圓錐擺的特征物理量、任意角速度對應的曲線方程、非慣性系中受力分析和切向加速度分析、與直桿以及圓形軌道約束的圓周運動對比分析.
學生在教師的引導下積極參與科學探究活動,主動獲取知識、發展探究能力.在解決實際問題的探究中深入理解原有的認知結構,構建新的物理知識結構體系,克服學生知識的分散和不系統等弊端;拓展探究為學生提供交流展示的平臺,收獲探究的樂趣與成功的喜悅,增強物理學習的興趣與信心;學生在合作、交流與評價中發現和反思自己的不足,培養學生的合作探究意識,有助于培養學生的發散思維和創新能力,克服認識的表面性、膚淺性,達到深度學習的目的,落實物理學科核心素養的教學目標.

