高考考查遞推公式的常見類型與解法

廖永福 林永志

(1.福建省廈門第二中學(xué) 361009；2.福建省仙游于潔小學(xué) 351256)

遞推公式是表示數(shù)列的一種方法，它揭示了相鄰幾項(xiàng)之間的關(guān)系，而項(xiàng)與項(xiàng)數(shù)之間的關(guān)系比較隱蔽，因此蒙上了一層神秘的面紗，給教學(xué)帶來一定的困難.解決這類問題的關(guān)鍵是選擇適當(dāng)?shù)姆椒ㄈデ髷?shù)列的通項(xiàng)公式，常用的方法有：定義法、公式法、累加法、累乘法、構(gòu)造法和歸納法等.現(xiàn)分述如下：

一、定義法

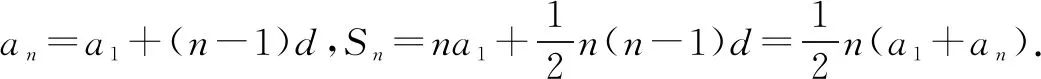
例1 (2020·全國卷Ⅱ) 數(shù)列{an}中，a1=2，am+n=aman，若ak+1+ak+2+…+ak+10=215-25，則k=( ).

A．2 B.3 C.4 D.5

分析令m=1，可得數(shù)列{an}是等比數(shù)列，求出數(shù)列{an}的通項(xiàng)公式，利用等比數(shù)列求和公式可列出關(guān)于k的方程，由k∈N*可求得k的值.

解答在等式am+n=aman中，令m=1，可得an+1=ana1=2an.

又a1=2，所以數(shù)列{an}是首項(xiàng)為2，公比為2的等比數(shù)列，an=2×2n-1=2n.

∴2k+1=25，則k+1=5，解得k=4.故選C.

點(diǎn)評本題考查遞推公式和等比數(shù)列的求和公式，考查計(jì)算能力和方程思想.關(guān)鍵是由遞推公式得出an+1=2an，進(jìn)而得出數(shù)列{an}是等比數(shù)列，屬于中等題.

二、公式法

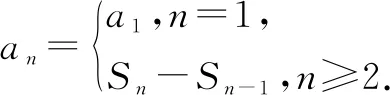
例2 (2020·江蘇卷))設(shè){an}是公差為d的等差數(shù)列，{bn}是公比為q的等比數(shù)列，已知數(shù)列{an+bn}的前n項(xiàng)和Sn=n2-n+2n-1(n∈N*)，則d+q的值是____.

分析由數(shù)列{an+bn}的前n項(xiàng)和Sn求出an+bn，再結(jié)合數(shù)列{an}是公差為d的等差數(shù)列，{bn}是公比為q的等比數(shù)列，求出d和q，進(jìn)而求出d+q的值.

解答數(shù)列{an+bn}的前n項(xiàng)和Sn=n2-n+2n-1(n∈N*)，

當(dāng)n≥2時，an+bn=Sn-Sn-1=2n-2+2n-1.

∵a1+b1=S1=1適合上式，∴an+bn=2n-2+2n-1(n∈N*).

又∵{an}是公差為d的等差數(shù)列，{bn}是公比為q的等比數(shù)列，

∴an=2n-2，bn=2n-1，

∴d=q=2，故d+q=2+2=4.

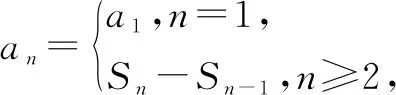
例3 (2012·全國卷大綱版)已知數(shù)列{an}的前n項(xiàng)和為Sn，a1=1，Sn=2an+1，則當(dāng)n>1時，Sn=( ).

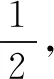
解法一由Sn=2an+1，得Sn-1=2an(n≥2).

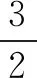
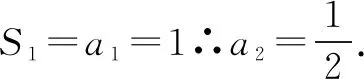
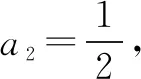
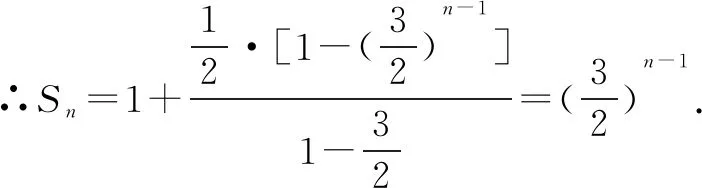
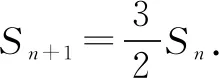
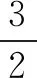
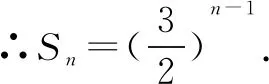
點(diǎn)評本題考查遞推公式與等比數(shù)列的通項(xiàng)公式、前n項(xiàng)和公式，考查推理能力與計(jì)算能力.消去an，還是消去Sn，要視具體情況而定，一般以簡便為原則，屬于中檔題．

三、累加法

形如an+1-an=f(n)的遞推公式，可用累加法求出an，即an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)，進(jìn)而解決問題.

例4 (2014·全國卷大綱版)數(shù)列{an}滿足a1=1，a2=2，an+2=2an+1-an+2．

(1)設(shè)bn=an+1-an，證明{bn}是等差數(shù)列；

(2)求{an}的通項(xiàng)公式．

分析(1)將an+2=2an+1-an+2變形為an+2-an+1=an+1-an+2，即bn+1=bn+2，根據(jù)等差數(shù)列的定義可以判定；(2)由(1)及等差數(shù)列的通項(xiàng)公式求出bn，代入bn=an+1-an，再用累加法求出{an}的通項(xiàng)公式．

解答(1)由an+2=2an+1-an+2得，an+2-an+1=an+1-an+2.

∵bn=an+1-an，∴bn+1=bn+2，即bn+1-bn=2.

又∵b1=a2-a1=1，∴{bn}是首項(xiàng)為1，公差為2的等差數(shù)列．

(2)由(1)得bn=1+2(n-1)=2n-1，即an+1-an=2n-1，又a1=1，

∴an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=1+1+3+5+…+2(n-1)-1

∴{an}的通項(xiàng)公式為an=n2-2n+2．

點(diǎn)評本題考查等差數(shù)列的定義、通項(xiàng)公式、前n項(xiàng)和公式，以及用累加法求數(shù)列的通項(xiàng)公式的方法，考查了轉(zhuǎn)化思想，屬于中檔題．

四、累乘法

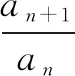
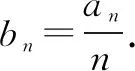
(1)求b1，b2，b3；

(2)判斷數(shù)列{bn}是否為等比數(shù)列，并說明理由；

(3)求{an}的通項(xiàng)公式．

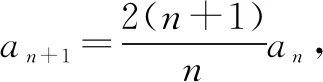
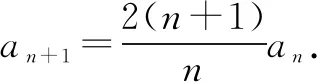
(2)數(shù)列{bn}是首項(xiàng)為1，公比為2的等比數(shù)列.

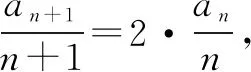
點(diǎn)評本題考查數(shù)列的遞推公式、等比數(shù)列的定義和通項(xiàng)公式．事實(shí)上，本題若用累乘法求解，則別有一番滋味，解答如下：

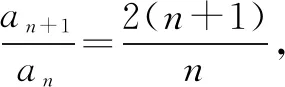
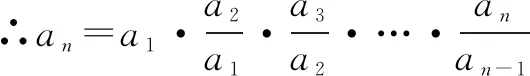
=n·2n-1.

∴an=n·2n-1，故bn=2n-1.至此，(1)(2)便迎刃而解.

五、構(gòu)造法

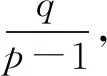
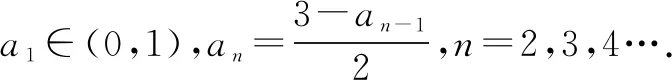
(1)求{an}的通項(xiàng)公式；

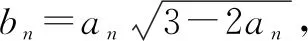
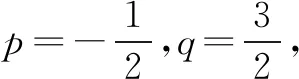
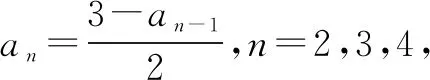
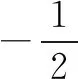
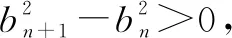
點(diǎn)評本題考查數(shù)列的遞推公式，等比數(shù)列的通項(xiàng)公式和不等式的證明等，解題時要認(rèn)真審題，注意挖掘題設(shè)中的隱含條件．用“同加法”構(gòu)造出等比數(shù)列是解題的關(guān)鍵，屬中檔題.

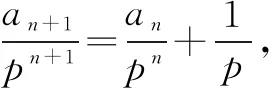
例7 (2009·全國卷Ⅱ)設(shè)數(shù)列{an}的前n項(xiàng)和為Sn，已知a1=1，Sn+1=4an+2(n∈N*)．

(1)設(shè)bn=an+1-2an，證明數(shù)列{bn}是等比數(shù)列；

(2)求數(shù)列{an}的通項(xiàng)公式．

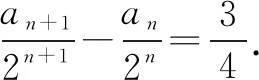
解答(1)由a1=1，及Sn+1=4an+2，得a1+a2=4a1+2，a2=3a1+2=5，所以b1=a2-2a1=3．

由Sn+1=4an+2，則當(dāng)n≥2時，有Sn=4an-1+2，兩式相減，得an+1=4an-4an-1，所以an+1-2an=2(an-2an-1)(n≥2).

∵bn=an+1-2an，∴bn=2bn-1(n≥2)，∴{bn}是首項(xiàng)為3，公比為2的等比數(shù)列．

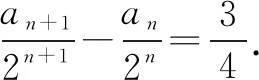
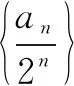
點(diǎn)評本題考查了等差數(shù)列和等比數(shù)列的通項(xiàng)公式，考查了定義法、公式法和構(gòu)造法，考查轉(zhuǎn)化和化歸思想和綜合運(yùn)用知識的能力．屬中難題.

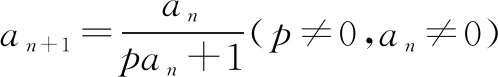
想一想：形如panan+1=an-an+1(p≠0,an≠0)的遞推公式，該怎樣變形？

例8 (2015·全國卷Ⅱ)設(shè)數(shù)列{an}的前n項(xiàng)和為Sn，且a1=-1，an+1=Sn+1Sn，則Sn=____．

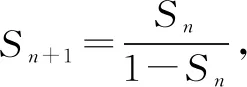
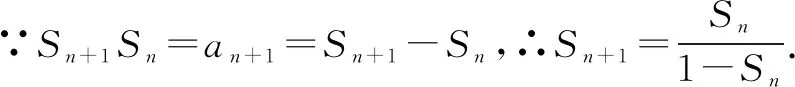
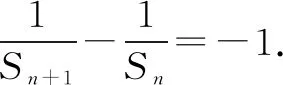
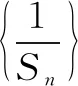
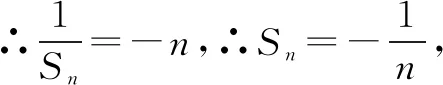
點(diǎn)評本題考查數(shù)列的遞推公式，等差數(shù)列的通項(xiàng)公式等，用同取倒數(shù)法構(gòu)造出等差數(shù)列是解決本題的關(guān)鍵，屬于中檔題．

六、歸納法

若題目所給的遞推公式不屬于上述情形，則可根據(jù)遞推公式計(jì)算出數(shù)列的一些項(xiàng)，觀察其特征、找出相應(yīng)的規(guī)律，歸納出一般性的結(jié)論并加以證明，進(jìn)而解決問題.

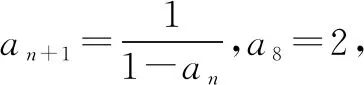
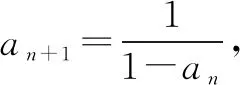
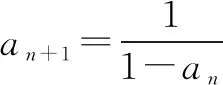
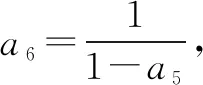
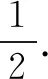
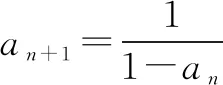
∴數(shù)列{an}是周期為3的周期數(shù)列.

點(diǎn)評本題考查數(shù)列的遞推公式和周期數(shù)列的性質(zhì)，關(guān)鍵在于從計(jì)算出數(shù)列的一些項(xiàng)中找出規(guī)律，歸納出一般性結(jié)論，屬于基礎(chǔ)題．

例10 (2020·全國卷Ⅲ)設(shè)數(shù)列{an}滿足a1=3，an+1=3an-4n.

(1)計(jì)算a2，a3，猜想{an}的通項(xiàng)公式并加以證明；

(2)求數(shù)列{2nan}的前n項(xiàng)和Sn.

分析(1)利用遞推公式計(jì)算a2,a3，猜想得出{an}的通項(xiàng)公式，再用數(shù)學(xué)歸納法證明；(2)用錯位相減法求解.

解答(1)由題意可得a2=3a1-4=9-4=5，a3=3a2-8=15-8=7.

由數(shù)列{an}的前三項(xiàng)可猜想數(shù)列{an}是以3為首項(xiàng)，2為公差的等差數(shù)列，即an=2n+1.

證明如下：當(dāng)n=1時，左端=a1=3，右端=2×1+1=3,成立.

假設(shè)當(dāng)n=k時，ak=2k+1成立,那么

當(dāng)n=k+1時，ak+1=3ak-4k=3(2k+1)-4k=2k+3=2(k+1)+1也成立.

故對任意的n∈N*，都有an=2n+1成立.

(2)由(1)可知，an·2n=(2n+1)·2n.

Sn=3×2+5×22+7×23+…+(2n-1)·2n-1+(2n+1)·2n①,

2Sn=3×22+5×23+7×24+…+(2n-1)·2n+(2n+1)·2n+1②.

由①-②，得-Sn=6+2×(22+23+…+2n)-(2n+1)·2n+1

∴Sn=(2n-1)·2n+1+2.

點(diǎn)評本題主要考查求等差數(shù)列的通項(xiàng)公式以及利用錯位相減法求數(shù)列的和，屬于中檔題.

遞推關(guān)系問題的考查形式靈活多樣，同時隱含著豐富的數(shù)學(xué)思想，解題時不僅要認(rèn)真審題，抓住遞推公式的特點(diǎn)，選擇適當(dāng)?shù)姆椒ǎ疫€要注重用函數(shù)與方程、轉(zhuǎn)化與化歸等數(shù)學(xué)思想方法指導(dǎo)解題實(shí)踐，把提升數(shù)學(xué)素養(yǎng)真正落到實(shí)處.