預應力作用下單箱單室箱梁剪力滯效應研究

晏 繼 偉

(蘭州局集團有限公司職工培訓中心，甘肅 蘭州 730050)

1 概述

預應力混凝土箱梁橋截面特性良好，整體性強，能有效抵抗彎矩和剪力[1]。預應力技術的引入，使得混凝土結構的變形被有效控制，裂縫的產生被推遲，構件的剛度得到提高，結構的耐久性得到改善，有助于改善旅客乘車的舒適性，提高列車高速運行時的安全性，滿足后期運營期間對線路平順性的要求。因此，這種結構被廣泛使用于橋梁建設中。PC箱梁由于其空間構造特點，將會產生剪力滯效應。近些年，中外研究人員做了大量關于箱梁的剪力滯效應的研究，但對于預應力引起的箱梁剪力滯效應，相關研究還不完善。樂小剛[2]、項貽強[3]、季文宇[4]等通過ansys軟件分別建立了預應力作用下的箱梁模型，使用等效荷載法，獲取了剪力滯系數，得出了一些關于預應力作用下的箱梁剪力滯現象的規律。

橋梁模型實驗是一種探索橋梁結構力學特性的有效手段，可以與理論研究相互印證。本文使用有機玻璃材料制作了單箱單室箱梁模型，進行了相關力學試驗。試驗時，在預應力束中設置壓力傳感器控制荷載大小，在跨中架設百分表測量梁體撓度，在典型截面處布置應變片獲取結構應變。本文在進行預應力荷載對單箱單室箱梁剪力滯效應的影響程度理論研究時，使用等效荷載理論，將預應力轉化為一般外荷載進行計算。然后，引入剪力滯翹曲位移函數[5]，即梁的縱向位移u(x,y,z)，以準確反應箱梁的撓曲變形。使用能量變分法研究剪力滯效應時，需根據最小勢能原理求解撓度和應力的解析解，計算解析解時剪力滯翹曲位移函數的選取很重要。這里使用三次剪力滯翹曲位移函數，根據現有文獻，三次模式精確度已經很高。

2 控制微分方程

2.1 基本假定

本文研究預應力作用下的箱梁剪力滯效應的方法為能量變分法，并基于以下各項基本假定[6-10]。

1)在翼板應變能計算時，假定板平面外的剪切變形、翼板豎向應變及橫向應變很小，可以不計入位能。

2)腹板在對稱荷載作用下，變形特性符合平截面假定。

3)箱梁橫截面中性軸位置在對稱荷載作用下，形心位置按照初等梁理論計算。

從理論上來說，箱形結構梁橋在發生彎曲變形時，截面中性軸的實際位置與基于初等梁理論的截面形心不再重合，因此需引入一個附加軸向位移[11]。

4)假定梁截面內力沿縱向的分布不受剪力滯的影響，剪力滯只改變梁截面正應力的分布。

5)箱梁腹板軸向變形采用平截面假定，在壓彎荷載作用下，在計算結構總應變能時不計算軸向變形產生的應變能。

6)定義w(x)為箱梁橫截面上任一點(x,y,z)的豎向彎曲撓度，w′(x)為該處的轉角，u(x,y,z)為縱向位移，U(x)為翼板剪切變形最大差，M(x)為沿梁長x處的截面彎矩，Q(x)為沿梁長x處的截面剪力。

箱梁截面示意圖見圖1。

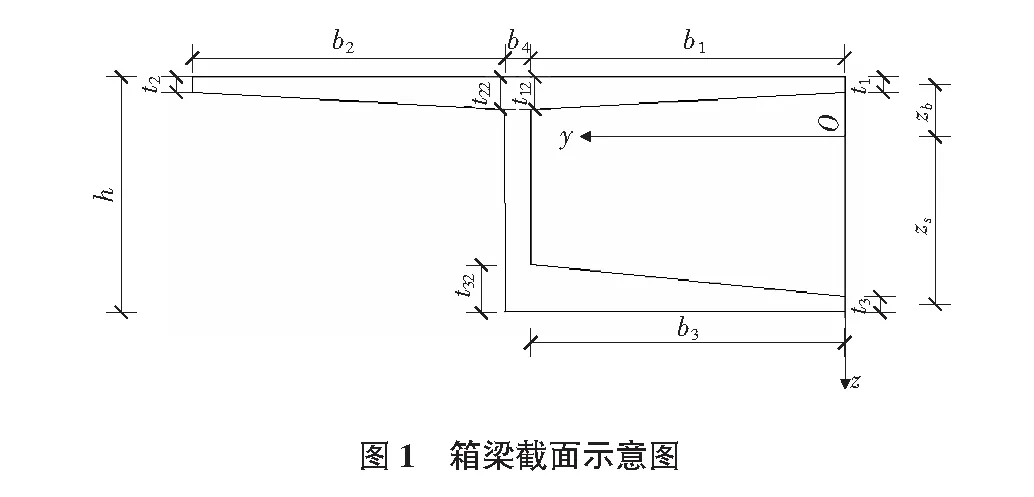
根據文獻[12]～[14]，選擇三次拋物線形函數f(y,z)為剪力滯翹曲位移函數，如下:

(1)

2.2 勢能表達式

用式(2)表示橫截面縱向位移u(x,y,z)，該式將剪力滯效應考慮在內。

u(x,y,z)=-zw′+f(y,z)U(x)

(2)

考慮截面縱向變形，可計算截面正應變ε、剪應變γ分別為：

(3)

(4)

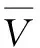
(5)

將式(3)，式(4)代入式(5),可得：

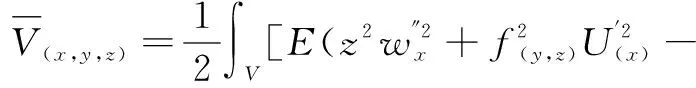
(6)

(7)

由式(6)和式(7)可得總勢能∏表達式為：

(8)

通過最小勢能原理可知，梁段在外力作用下產生位能，對總位能∏取變分，值為0。

(9)

2.3 控制微分方程組

考慮預應力箱梁剪力滯效應，結合式(8)，式(9)兩式進行變分計算，可得出控制微分方程和邊界條件為：

(10)

由式(10)前兩式可得:

(11)

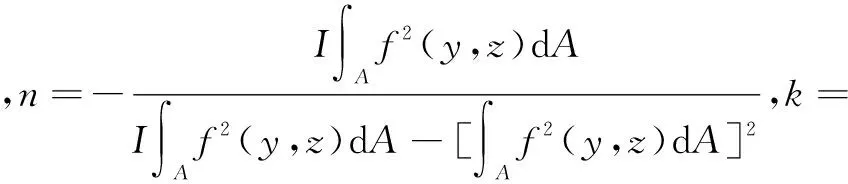
2.4 邊界條件

此處針對典型簡支梁邊界條件進行求解分析。對于固定端，邊界條件為：

U(x)=0,δU(x)=0

(12)

對于非固定端假設梁端，邊界條件為：

(13)

2.5 剪力滯應力計算式

考慮式(2)，結合胡克定律，截面任一位置縱向應力σ(x,y,z)為：

(14)

由式(14)可知，剪力滯現象在跨中位置不存在。

3 剪力滯效應縮尺模型實驗概況

3.1 箱梁基本情況及材料特性

橋梁模型實驗是一種探索橋梁結構力學特性的有效手段，現制作跨度L=1 m的有機玻璃等截面箱梁模型，橫截面如圖2所示。選用公稱直徑3 mm的低松弛、高強鋼絲線作為預應力筋。

為獲取有機玻璃材料真實力學參數，預制試件，進行力學拉伸實驗，得到模型所用材料彈性模量E=2 600 MPa，泊松μ=0.385。

3.2 加載裝置及測點布置

實驗采取雙點對稱加載的方法，兩側對稱布置預應力鋼束，荷載大小通過每束束筋中布置的壓力傳感器進行控制。實驗加載情況如圖3所示。

實驗時，把應變片布置于典型截面處。在跨中、L/4跨以及L/8跨頂板共設置27個應變測點，三處橫向位置相同，于底板處設置15個應變測點。在緊鄰錨固端的L/8跨處設置一組應變測點，以獲取應力從預應力錨固端向跨內傳遞過程中的應力擴散特征，箱體橫截面應變測點布設位置見圖4。

實驗時，使用精密百分表位移計測量各種實驗工況下的撓度變形情況，并根據百分表的指針變化幅度輔助判斷梁體變形是否達到相對穩定。讀取應變讀數時，位置計讀數波動值需在精度范圍之內。百分表位移計設置在跨中腹板與底板相交處，撓度測試見圖5。

4 實驗結果與分析

4.1 荷載—撓度關系

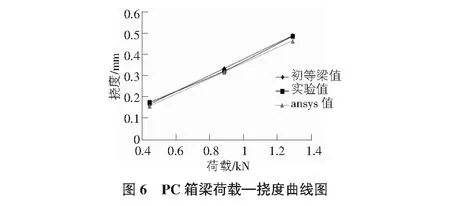
實驗梁體跨中位置荷載—撓度變化情況見圖6。從中可以發現，有限元解與實驗解相接近，說明了實驗解和本文理論解的精度很高；同時可以看出如果不計算剪切變形引起的撓度增大，僅按初等梁理論計算，得出的撓度值往往偏小。

4.2 橫橋向應變分析

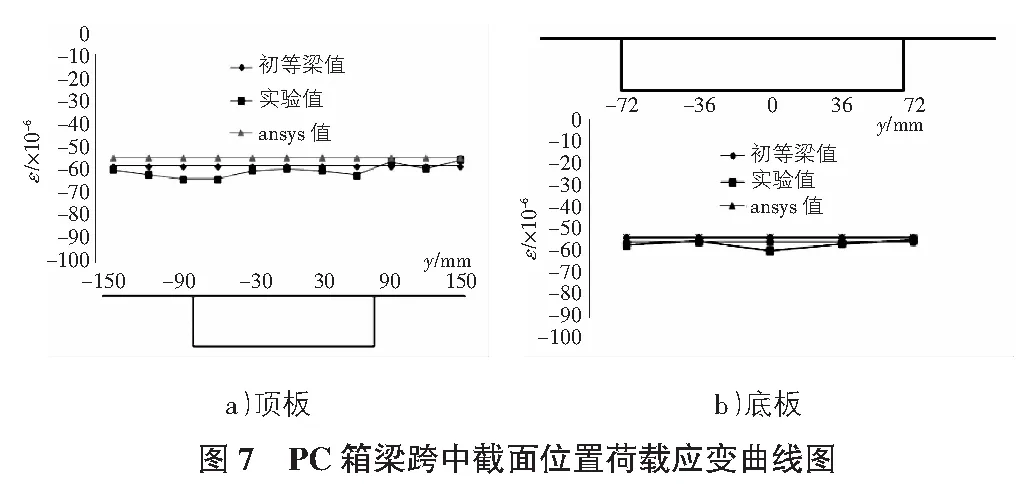
從圖7中可以看出，跨中頂、底板截面各點處實驗值有波動，考慮到實驗值的離散型，結合有限元解及初等梁解進行數據分析，可以發現此截面各點縱向應變均勻，不存在剪力滯現象。這是由于跨中截面距離受力點較遠，處于純彎曲受力狀態，結果亦符合前文理論推導。

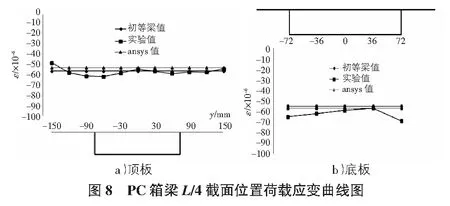
圖8為梁體L/4位置處應變分布情況，可以看出，該截面應力變化也不存在剪力滯特點，與跨中應變的分布相比，該位置數據方差大于跨中位置，存在一定離散型。

圖9為L/8截面處應變分布情況，該截面應變值變化較大，按照初等梁理論得出的應變值與真實應變值最大相差29%，可知此位置處存在顯著的剪力滯現象，而且頂板變化程度要高于底板。

4.3 順橋向應變分析

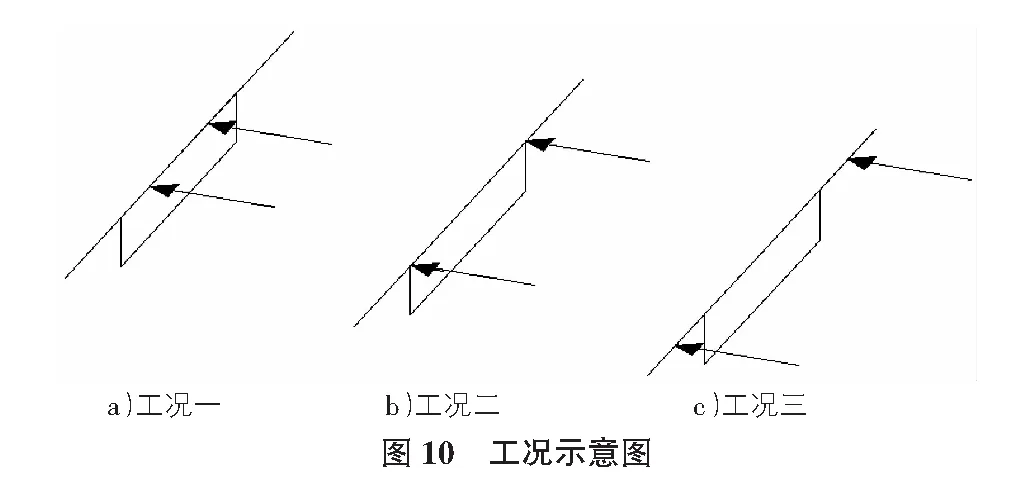
從圖10中可以發現，改變梁體頂底板預應力束布置位置，則相關受力點附近的應力會產生很大變化。現對梁體頂板、腹板相交點展開研究，分析沿梁長方向縱向應力的分布規律，探究梁體軸力位置變化與箱梁的剪力滯現象的關聯性。

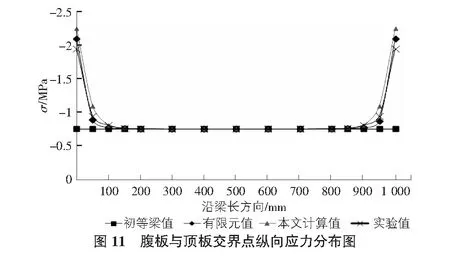
如圖11所示，當預應力作用在頂板時，沿梁長方向腹板與頂板交界點處的縱向應力并非均值，梁端處應力值明顯大于跨中；當靠近作用點時，截面應力明顯增大，最大值為初等梁值的3倍。

如果改變預應力束筋布置位置，則會引起梁端一定范圍Le內橫截面應力的改變，此范圍Le約等于梁體結構腹板間的間距。此范圍之外各處應力值與初等梁計算值一致，橫截面應力值沿梁長方向均勻分布，不存在剪力滯效應，可將梁體視為純彎曲受力狀態；同時，預應力束位置的變化不會引起此范圍內截面應力值的變化。

5 結語

1)本文所用實驗系統能夠有效模擬預應力作用下箱梁的受力情況。本文制作了縮尺單箱單室模型，以預應力等效荷載理論為依據，模擬了預應力箱梁受力特征，并使用自行設計的實驗加載裝置進行了各項試驗，得出了各項試驗數據，所得數據與本文理論解，有限元板殼數值解，初等梁理論解相一致。

2)總體來看，梁端至一定范圍Le內，截面應力值與初等梁計算值不一致，越接近梁端，兩者偏差越大，最大處在梁端，兩者相差3倍。如果距梁端位置大于Le，則初等梁計算值與截面實際應力值相一致。另外，預應力直線束筋位置的改變會影響梁體中梁端至一定范圍內Le內的應力的分布。

3)總體來看，當預應力束筋按直線形式對稱布置時，單箱單室PC箱梁不存在剪力滯現象，而梁端附近的橫截面應力變化是力的應力傳遞路徑導致的。當PC箱梁中預應力束筋按照直線形式布設時，梁體L/8截面應力變化很大，L/4截面應力分布不均勻，跨中位置和初等梁解相同，沒有剪力滯現象產生。

4)在箱梁中布置預應力筋能大幅度提高梁體承載能力，預應力筋在設計時一般會選擇集中布置，這會導致布束點附近存在明顯的應力集中現象，梁端處應力值會劇烈變化，如果只是按照初等梁理論簡單計算，布束設計時不考慮該因素，會使得梁端頂板、底板處梁體開裂，引起橋梁病害。