布料模擬濾波方法在鐵路勘測LiDAR中的應用

李 特

(中國鐵路設計集團有限公司，天津 300251)

隨著無人機、慣性導航和激光測距技術的快速發展，機載激光雷達技術在鐵路勘察設計項目中的應用越來越廣泛[1]。機載雷達是一種主動遙感技術，不受時間、氣候的影響，可以全天候獲取地面的三維信息[2]。利用機載LiDAR獲取的三維點云數據，其點云密度較高，可以建立高精度的DEM模型并切繪出鐵路的橫斷面。在建立DEM模型時，需要對原始的點云進行濾波(區分地面點和非地面點)。

目前，點云濾波算法大致分為基于坡度的點云濾波、基于數學形態學的點云濾波和基于表面的濾波[3-4]。基于坡度的濾波算法是假設地形坡度在某一地域范圍內逐漸變化，而建筑或樹木與地面之間的坡度變化相對較大，基于這一假設，通過比較LiDAR點與其相鄰點的斜率區分地面點和非地面點，但此方法難以在復雜地形中發揮良好的作用[5-6]。數學形態學濾波算法是利用數學形態學思想去除非地面點[7-8]，一般會設置合適的濾波窗口。若濾波窗口過大則會平滑掉地形細節，如山脊、懸崖等，窗口過小則會保留大的建筑物點，故需要通過豐富的先驗知識定義合適的窗口尺寸[9]。基于表面的s波方法是通過迭代來篩選地面點，這種濾波方法的核心是需要建立一個裸露地表面。典型代表有自適應不規則三角網濾波(Triangulated Irregular Network，TIN)算法[10]，但該算法需要設置整個區域的閾值參數，故難以在折線和陡峭地形附近檢測到地面點，Bayram E[11]等介紹一種基于曲面的濾波方法，引入加權最小二乘插值來識別地面點，結果表明該方法在平坦地形上效果良好，但在坡度陡、變異性大的地形上可靠性較差。

綜上所述，傳統的濾波算法在特定區域的運用較為成功，但其性能會隨著地形特征不同而變化，在復雜的城市景觀地區和地形陡峭的山區，濾波結果具有爭議性[12]。此外，以上濾波方法的實現還需要合適的參數才能達到滿意的效果，而這些參數由于區域地形特征的不同而很難確定。

為了解決上述問題，介紹一種布料模擬濾波算法(cloth simulation filter，CSF)[13]，該算法以一種“自下而上”的策略逼近地面點，參數較少。張昌賽等利用不同坡度、點云密度、不同覆蓋物測試數據對布料模擬濾波算法進行適用性分析，結果表明其誤差率小，效率高[14-15]。相較于現有的濾波算法，CSF濾波方法具有一定優勢[16]：①人為設置參數少，且參數易于理解和設置，不需要過多經驗知識；②在平坦、山區和建筑物密集的不同地形場景中，其參數一致性較好。

1 CSF濾波方法

1.1 CSF算法原理概述

布料模擬是計算機圖形學的專業術語，是一種基于物理過程的假設模擬。其思想是假設一塊布隨著重力自由下落，如果布料極其柔軟可以貼在地面上，則布料的最終形狀則是數字表面模型((Digital Surface Model，DSM)。基于此思想，若將獲取的點云數據進行倒置，將布料賦予剛性特點，則布料的最終形狀就是DEM(見圖1)。

圖1 布料模擬算法

為了從原始點云中提取地面點，模擬布料結構中會有許多節點，程序通過分析粒子節點與鄰近LiDAR點云相應點之間的相互作用，確定出最符合真實地形的節點分布位置，進而確定布料最終形狀，從而可以將原始點云區分為地面點和非地面點。

在程序仿真布料模擬過程中，圖中每一個粒子均帶有質量信息，粒子之間相互連接的網絡模型稱為Mass-Spring模型(見圖2)。粒子在三維空間中的分布位置和形狀決定了布的形狀，粒子之間的互連網絡遵循一定力的性質特點，相當于在粒子之間安置了彈簧。為了模擬布的形狀，可設置優化函數對其進行求解。

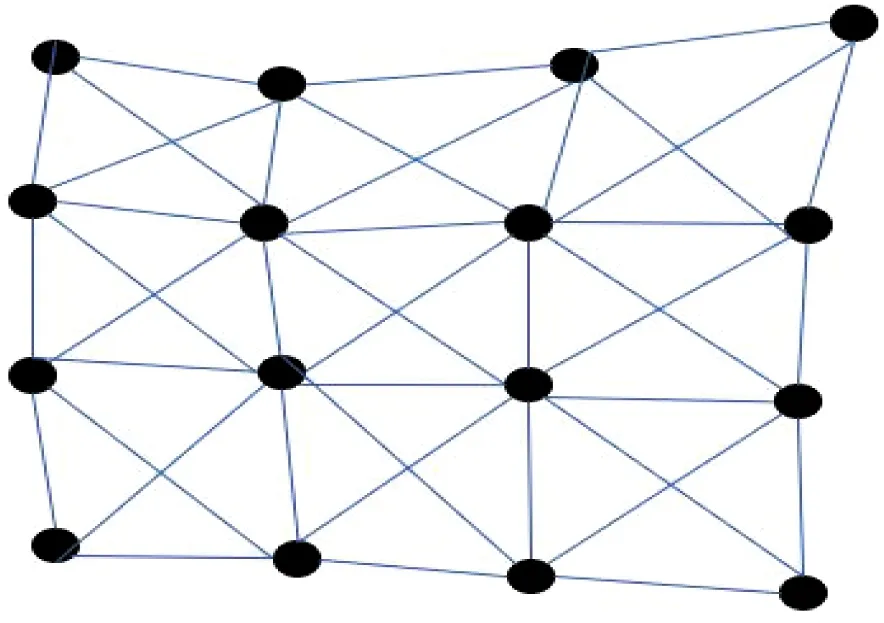
圖2 網絡模型結構

式中，X表示t時刻粒子的位置，Fext(X，t)表示粒子運動時受到的外力，Fint(X，t)表示粒子在位置X和時間t時刻的內力(相互連接的力)。內部力和外部力隨著時間t變化而變化，因而可以通過數值積分來求解。

1.2 程序設計流程

算法詳細步驟如圖3所示。

圖3 算法流程

(1)對點云進行預處理，去除原始點云中的噪聲和異常值。將預處理后的點云進行翻轉，將末次回波點置于上方。

(2)將空間中的粒子位置和LiDAR點云投影到同一水平面，根據設置的超參數空間分辨率GR(相鄰粒子之間的距離)確定粒子個數Np，并找到每個網格中離粒子最近的LiDAR點(命名為CP點)，布料模擬過程中各個粒子的初始值Xinit一般為最高點以上，后續迭代會進行不斷糾正。

(3)定義一個IHV(交點高度值)，即CP點在投影前的高度值，該值會限制粒子移動的范圍。當粒子移動到IHV時，表明已經到達臨界最低位置，粒子狀態變為停止移動。在優化過程中，每一次迭代都會將粒子當前高度值CHV(粒子迭代當前高度值)與IHV進行比較。當CHV等于或者低于IHV時，粒子被認為回到IHV位置，并標記為不可移動點。

(4)在獲取所有粒子的三維位置后，可以得到真實地形的近似值，通過計算粒子與原始激光點Xp之間的距離和人為設置的參數閾值(thread)，實現將原始LiDAR點云分為地面點和非地面點(低于或等于閾值為地面點，高于閾值為非地面點)。

1.3 算法實現

在算法研究基礎上，采用基于PCL庫C++語言編程，研發點云濾波小插件，并利用Qt框架搭建圖形界面(見圖4)。

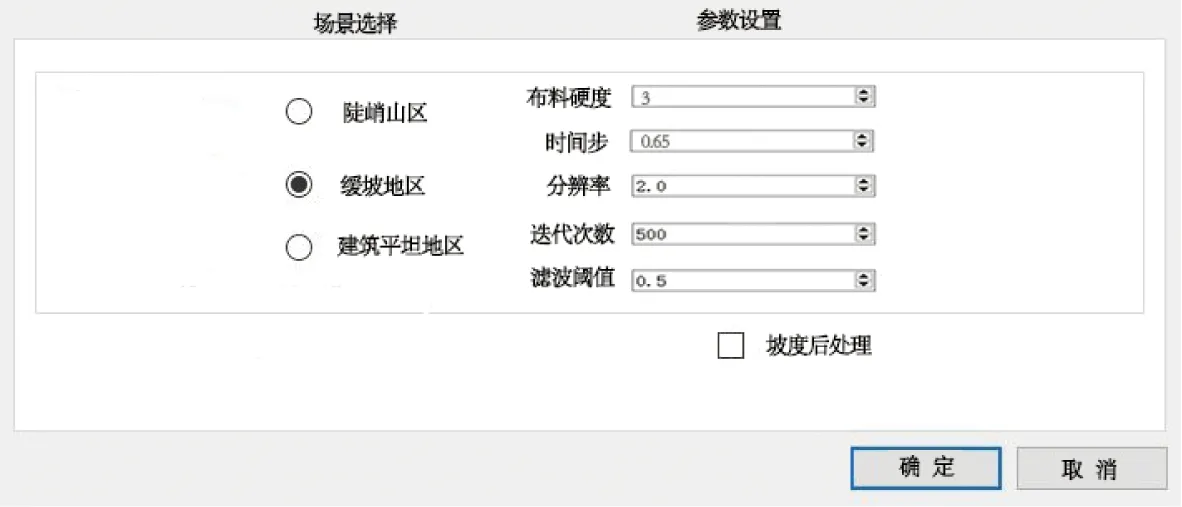
圖4 算法實現界面

整個布料模擬過程中，除了算法的自動約束條件外，還需人為指定5個超參數。①布料硬度：控制粒子節點隨重力下降的幅度；②時間步：控制著粒子移動的位移；③網格的分辨率GR：代表布料中相鄰粒子之間的距離，一般設置為2 m左右(數值過小則迭代計算慢)；④最大迭代次數iteration：表示算法迭代終止的臨界值；⑤分類閾值thread：表示將點云分為地面點和非地面點的閾值(根據不同場景而定，一般設置為0.5 m)。針對陡坡區域，由于粒子位于實際點云位置上方，其濾波易出現錯誤點。為了解決此問題，對于陡坡區域，應進一步限制粒子間的移動關系，平滑陡坡的邊緣，達到與實際地形相符的效果。

2 精度評定方法

與遙感影像分類類似，點云濾波結果也需要定量評價，因而需要建立真實的標簽數據作為groundtruth。通過手動分類建立測試數據集，即測試數據已經明確地面點和非地面點，將其濾波結果與groundtruth作比較，算出評價因子。評價體系采用國際攝影測量與遙感學會的交叉表評價因子(見表1)。

表1 交叉表

為了評價濾波結果可靠性，以總誤差作為指標，表示分類結果與groundtruth不一致的概率值，有

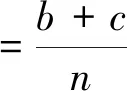
(2)

同時，與遙感影像分類結果評價類似，利用kappa系數作為檢驗方法，kappa系數越高，表明濾波效果越好，有

(3)

3 實例測試與分析

3.1 數據準備

選用兩塊不同地形場景數據a和b作為測試數據，a為地形起伏大的山區，有陡坎且植被覆蓋茂盛；b為建筑物密集的城區，地勢較平坦，有植被和高大建筑物。這些測試數據均已進行人工精細分類，每個三維坐標點均有屬性類別信息(見圖5、表2)。

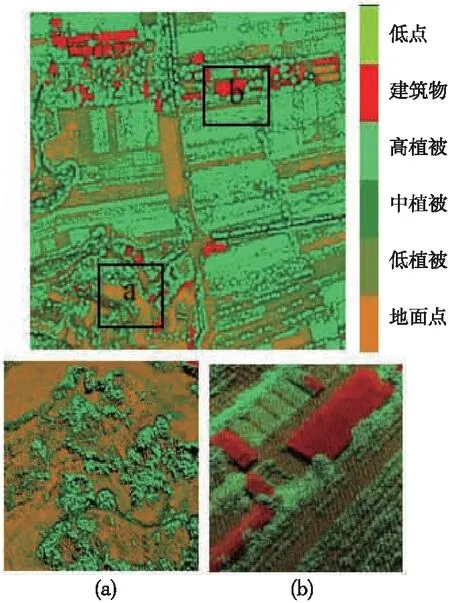
圖5 測試數據

表2 測試數據集特征(pt表示points)

3.2 結果分析

為了測試CSF點云濾波算法適用性，將測試數據a和b作為實驗驗證數據，通過比較濾波后結果和真實驗證數據的總誤差、kappa系數評價算法的可靠性。同時，為了比較不同算法的差異性，實驗還將CSF濾波算法與傳統的基于數學形態學濾波方法、基于TIN濾波方法進行對比分析，分析測試數據在不同濾波方法上的濾波總誤差kappa系數。

在一些陡坡區域，形態學濾波容易將地面點歸類為低植被點；在坡度較大地區地面點極其稀疏，在生成DEM模型時，容易將坡度細節區域忽略(見圖6(a))。當真實場景為過渡緩坡時，通過數學形態學濾波方法建立的DEM模型表現為陡坎(見圖7(a))。基于TIN的點云濾波算法其搜索的地面點不連續，點與點之間空洞比較大，在靠近坡底的區域地面點較少，因而建立的DEM模型在坡度區域易出現“尖刺”現象(見圖7(b))。CSF濾波算法在坡度較陡的區域，過濾出的地面點較多且連續，建立的DEM三角網模型能夠充分利用這些地面點，因而其模型較為接近真實場景。

在植被茂盛地區，自上而下的地面點搜索策略容易受植被或建筑物點的影響，而CSF是自下而上的地面點濾波算法，因而搜索地面點較為有利。在植被和建筑物混合區域，形態學濾波算法和基于TIN的濾波算法均能搜索到地面點，但搜到的地面點較稀疏，并夾雜低植被點(見圖6(b))。相比而言，CSF算法搜索到的地面點分布更為合理。

圖6 基于形態學、基于TIN和基于CSF濾波后剖面

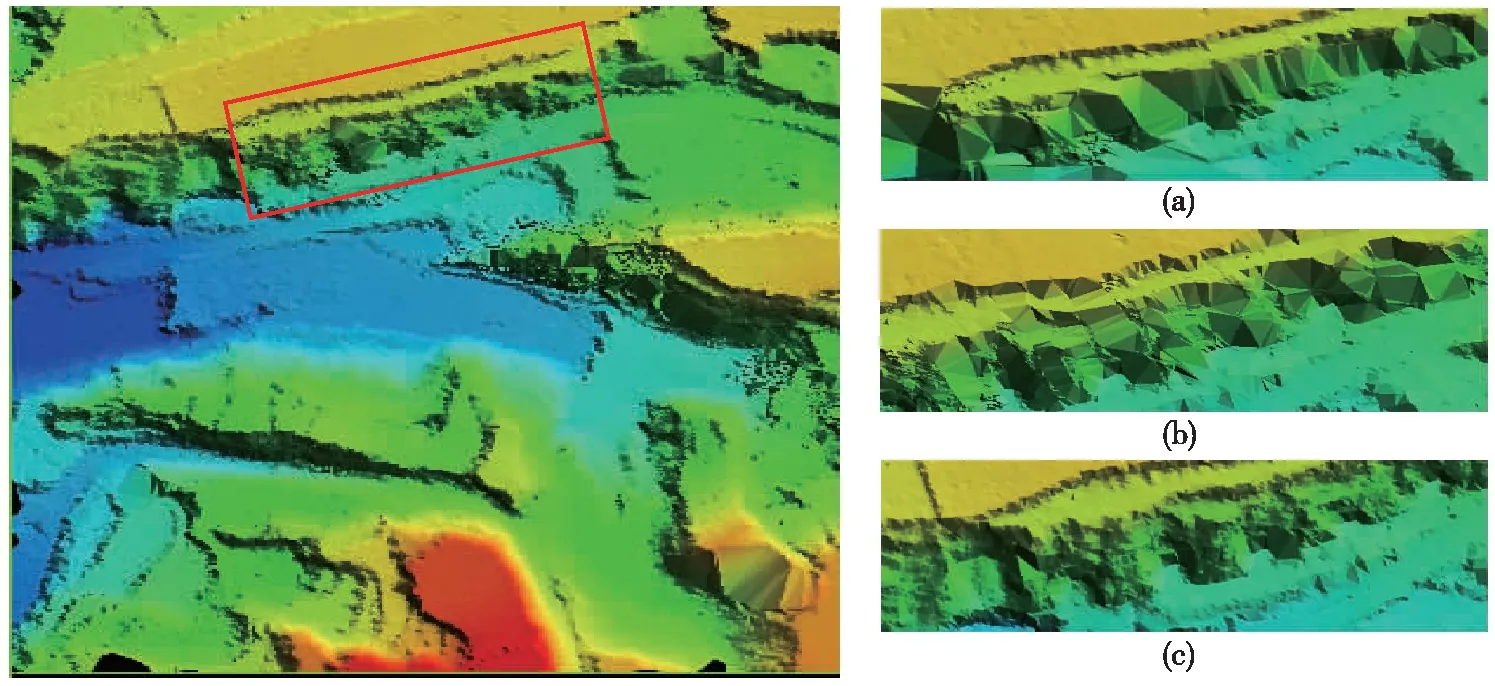
圖7 DEM模型

3.3 精度評定

對比分析數學形態學濾波、基于TIN和CSF濾波算法在不同場景下的總誤差和kappa系數。研究結果表明(見表3、表4)，CSF濾波算法在測試數據下要優于傳統的點云濾波算法。針對數據a，CSF相比形態學和TIN，總誤差分別減小了15.79%、5.91%，kappa系數分別提高了14.41%、9.09%；針對數據b，其總誤差分別減小了10.82%、4.18%，kappa系數分別提高了11.55%、4.38%。CSF濾波算法總誤差低于11%，表明濾波結果與手動分類建立的參考數據一致性較為良好(默認手動分類結果正確)，其kappa系數優于92%，表明濾波效果良好。

表3 總誤差 %

表4 kappa系數 %

CSF算法處理效率與分辨率GR、迭代次數iteration、粒子移動時間步長有關。一般而言，在地形較復雜的山區，粒子到達局部最優位置的迭代次數有所增加，其處理效率會有所下降。本次采用的測試數據范圍較小，3種算法在處理效率上未見明顯差別。

4 結論

(1)布料模擬的點云濾波方法是通過模擬布料貼近地面的物理過程，以不斷迭代來獲取原始LiDAR點云的地面點。相較于傳統的點云濾波算法，其參數少，且易于設置。在不同的地形場景下，參數的變化不大，濾波效果穩定。

(2)在一些植被茂密且地形相對復雜的區域，坡度變化是影響點云濾波的重要因素，一般的算法在濾波過程中往往難以獲取到連續地面點，造成大量地面點出現空洞現象，其后續建立的DEM模型易出現“尖刺”現象或忽略陡坡細節。CSF算法通過布料模擬過程搜尋地面點，并經坡度后處理策略可以解決此類問題。

(3)為了進一步提高CSF算法的性能，在后續研究中將深化研究CSF參數自適應化。