緊鄰鐵路深基坑鉆孔樁支護嵌入深度研究
鄧昌霞
(中鐵十八局集團市政工程有限公司,天津 300222)
隨著我國國民經濟的發展,地面交通的數量和規模越來越大,鐵路、公路網絡相互交叉,導致交通設施越來越擁擠。受環境、規劃等因素的制約,許多下穿道路通道或者上跨線路橋墩的基坑修建在既有線旁。基坑的開挖改變了原有土體的應力場和變形場,引起既有線路產生不利變形[1-3]。當基坑緊鄰既有線路時,基坑開挖施工的不利影響尤為顯著[4-5]。為降低既有線路的附加變形,提高既有線路的安全性,常采用鉆孔樁在靠近既有線路一側的坑壁進行支護加固方式[6],其嵌入深度是重要的設計參數,會對基坑的穩定性及既有線路的變形產生巨大影響[7-9]。
目前,計算支護樁嵌入深度主要基于經典土力學理論的極限平衡法[10],即不考慮樁與土體之間的相互影響,將鉆孔樁系統形成的支護結構視作受力結構,然后基于郎肯土壓力法計算樁背側的主動土壓力和樁前側的被動土壓力,最后通過力矩平衡方程求得嵌入樁底深度[11-12]。然而,這種方法不能考慮開挖卸荷效應,其計算結果與基坑開挖施工過程真實應力存在顯著差異。
以某緊鄰既有鐵路的深基坑為研究對象,首先建立基坑和支護樁的二維剛性極限平衡分析模型,采用郎肯土壓力計算方法得到樁背主動土壓力和樁前被動土壓力,進而計算出基樁嵌入坑底的解析計算深度;然后,基于有限元方法建立數值分析模型,分析研究不同嵌入深度條件下地表沉陷、坑底隆起和基樁撓曲變形規律[13-15],研究既有鐵路路基變形受嵌入深度變化的影響規律,探求鉆孔樁的最優嵌入深度,并與基于極限平衡分析模型得到的嵌入深度進行對比。
1 工程概況
某框架橋施工基坑深約9 m,寬約10 m,長約60 m,基坑延伸方向一側緊鄰既有鐵路,靠近既有鐵路一側坑壁采用鉆孔樁進行支護,鉆孔φ1.25 m@1.5 m,基坑另外三面采用1∶0.5放坡。基坑斷面如圖1所示。

圖1 基坑設計斷面(單位:m)
基坑開挖土層主要為細圓礫土和粉質黏土。細圓土層呈黃褐色,稍濕,稍密-中密,含約50%圓礫,原巖以安山巖及凝灰巖為主,一般粒徑為20~40 mm,最大70 mm,呈渾圓狀,充填物為中粗砂及少量粉質黏土,常夾有粉土、粉質黏土薄層及透鏡體;粉質黏土層呈黃褐色,硬塑,以粉黏粒為主,切面光滑,含少量細顆粒。細圓礫土層和粉質黏土層交替水平出現,從上至下分布情況為:細圓礫土(6.3 m)、粉質黏土(3.6 m)、細圓礫土(5.0 m)、粉質黏土(10 m)。此處地下水埋深距地表20~22 m。根據現場原位試驗獲得的細圓礫土層和粉質黏土層的物理力學參數見表1。 鉆孔樁施工過程中,采用泥漿護壁方式成孔,樁孔質檢合格后安放鋼筋籠并灌注混凝土。混凝土標號為C35,鋼筋籠的縱向鋼筋為HRB335,水平鋼筋為HPB235,交接處焊接。根據混凝土設計規范,鉆孔樁力學參數見表1。
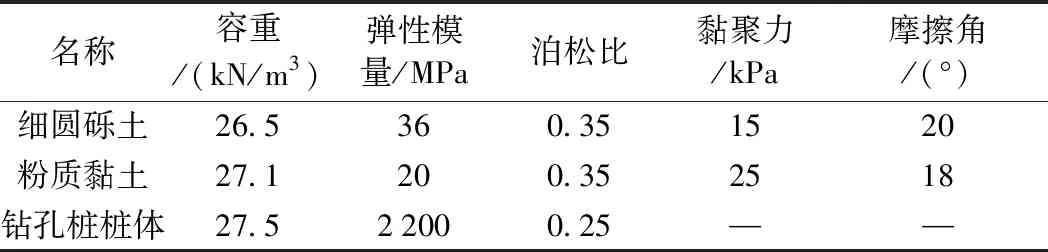
表1 土層及樁體力學參數
2 基于極限平衡方法的嵌入深度計算
假設計算高度h=20 m,由于各土層物理力學參數差別不大,故采用加權算法計算平均土壓力。

26.76 (kN/m2)
(1)

(2)
(3)
主動土壓力系數Ka為

(4)
被動土壓力系數Kp為

(5)
主動土壓力強度Pa為
(26.76×h)×0.51-2×19.35×0.71=
(13.65h-27.48) kPa
(6)
被動土壓力強度Pp為
(26.76×h)×1.96+2×20.45×1.40=
(52.45h+57.26) kPa
(7)
迎土區土壓力為零點的高度h為

(8)
迎土區基坑底土壓力P1為
26.76×9×0.51-2×19.35×0.71=95.35 kPa
(9)
背土區基坑底土壓力P2為
0+2×20.45×1.40=57.26 kPa
(10)
根據以上計算數據,主動土壓力強度和被動土壓力強度分布如圖2所示。
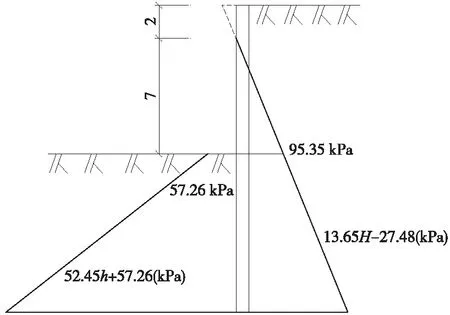
圖2 土壓力強度隨深度變化(單位:m)
假設距離坑底h處的主動土壓力和被動土壓力相等,即
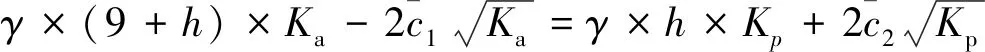
(11)
解得
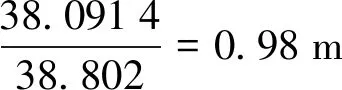
(12)
因為迎土區的主動土壓力強度和背土區的被動土壓力強度方向相反,所以在深基坑底部以下的范圍內土壓力可以相減,化簡后的土壓力強度線如圖3所示。
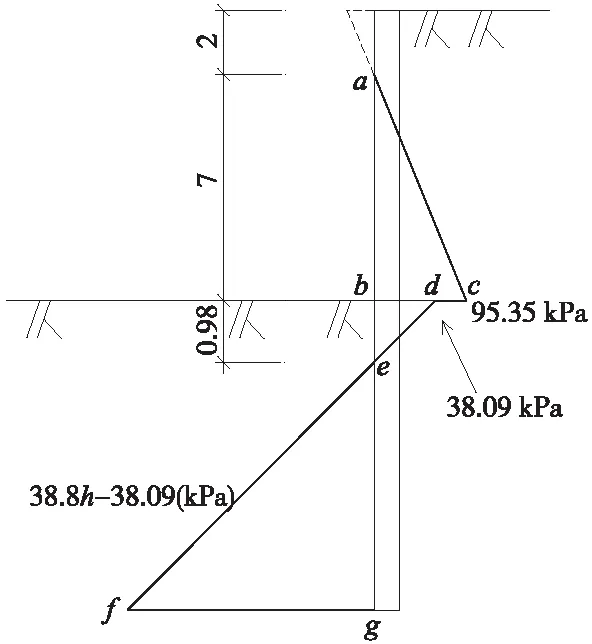
圖3 簡化后的土壓力強度隨深度變化(單位:m)
假設埋入深度為h,將主動土壓力強度abc和bde,以及被動土壓力efg對g點取力矩,使得efg產生的抵抗力矩大于由abc和bde所產生的傾覆力矩的2倍(即安全系數為2),有
M抵抗≥2M傾覆
(13)
式中,M抵抗是被動土壓力對g點產生的力矩(為順時針),M傾覆是主動土壓力對g點產生的力矩(為逆時針)。進一步得到
2×(F1×e1+F2×e2)
(14)
式中:h—深基坑底以下深度/m;Pp—被動土壓力強度/kPa;Pa—被動土壓力強度/kPa;e—土壓力強度efg的作用點到g點的力矩;F1—主動土壓力強度abc的合力/kN;e1—合力F1到g點的力矩;F2—主動土壓力強度bde的合力/kN;e2—合力F2到g點的力矩。
式(14)中,各個變量的計算式為

(15)
將式(15)代入到式(14)中,有
12.934h3-0.280 46h2-1 446.462 474h-
3 061.416 2≥0
(16)
求解式(16),得到鉆孔樁最小嵌入坑底深度(h=11.52 m)。為確保樁的穩定,在已求得的鋼板樁入土深度基礎上,乘1.15系數,增加鋼板樁埋入土體的長度。因此,鉆孔樁的最終長度為
11.52×(1+0.15)+9=22.25≈23 m
(17)
3 不同嵌入深度對變形影響規律研究
利用有限元軟件Phase Ⅱ建立基坑平面的二維應變模型,土體采用三角形單元,屈服準則采用摩爾庫倫準則,力學參數見表1,鉆孔樁采用襯砌單元(liner)進行模擬,土層共分為4層,從上至下依次為:細圓礫土①、粉質黏土①、細圓礫土②、粉質黏土②。基坑分4步開挖,嵌入深度考慮8種情況:1 m、3 m、5 m、7 m、9 m、11 m、13 m、15 m。數值分析網格模型見圖4。由圖4可知,模型頂部無約束,其它3個側面約束法向位移,在模擬過程中,先進行初始地應力平衡,然后設置鉆孔樁,最后分步開挖土體,觀測開挖完成后的坑底和鉆孔樁側基坑變形。

圖4 基坑開挖的網格模型
圖5和圖6分別表示不同嵌入深度條件下坑底隆起和右側坑壁的變形曲線。由圖5可知,坑底隆起變形特征是中間大、兩端小,但是左側隆起幅度要大于右側隆起幅度,這是由于右側鉆孔樁可以在一定程度上約束土體的側向擠壓位移,另外,隨著嵌入深度的增大,隆起變形曲線在坐標軸中是整體下降的,表明增大嵌入深度可以有效降低坑底隆起變形。由圖6可知,基坑側壁變形呈現鼓脹的形式,即頂部和底部變形小、中部變形大,鉆孔樁呈現一定程度撓曲現象。另外,隨著嵌入深度的增大,側壁變形曲線整體下降,表明嵌入深度越大,側壁變形越小,提高鉆孔樁的深度可在一定程度上限制側壁變形。
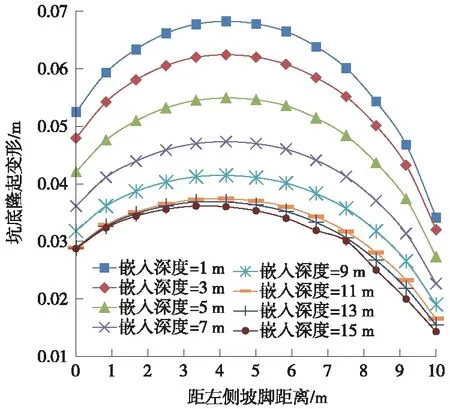
圖5 坑底隆起變形曲線
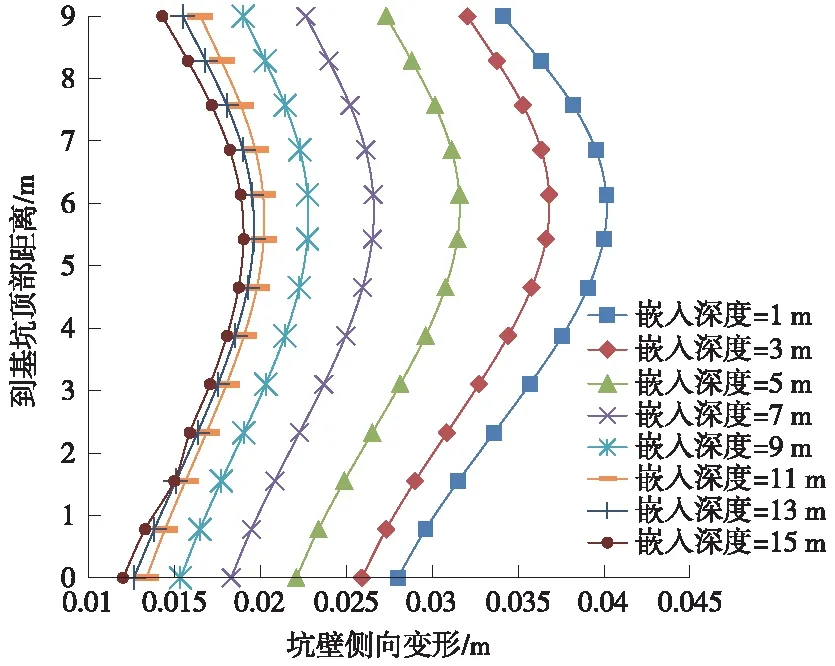
圖6 坑壁側向變形曲線
為進一步研究隆起變形、側壁變形與嵌入深度的關系,圖7和圖8展示了隆起變形和側壁變形隨嵌入深度的演化曲線。由圖7和圖8可知,隨著嵌入深度的增大,隆起變形和側壁變形均開始顯著降低,隨著嵌入深度的進一步增大,隆起變形和側壁變形不再隨嵌入深度增大而降低,這說明存在一個最優嵌入深度。分析可知,12 m是嵌入深度曲線的拐點。因此,可認為12 m是該基坑的最優嵌入深度,定義變量δ來表征最優嵌入深度,即

(18)
式中,D表示嵌入深度/m;H表示基坑深度/m。最優嵌入深度比取1.33。

圖7 坑底隆起變形隨嵌入深度的變化曲線

圖8 基坑側壁變形隨嵌入深度的變化曲線

圖9 最大主應力
圖9~圖12分別表示嵌入深度為12 m時基坑開挖完成后的最大主應力、最小主應力、位移和塑性區分布。由圖9~圖12可知,基坑開挖后,坡腳位移為3 cm時,坑底隆起約5 cm,左側邊坡體未產生大的變形和滑移,右側防護樁一側基坑位移僅有2 cm左右。由圖12可知,基坑邊坡土體未發生塑性破壞。另外,基坑底部出現應力釋放,這也是坑底略微隆起的原因。防護樁在與基坑底部相同高程處應力較為集中,在靠近基坑一側,出現了明顯壓應力集中區,最大壓應力為0.2 MPa,在背離基坑一側,出現了明顯拉應力集中區,最大拉應力為0.3 MPa。防護樁所受的最大拉壓應力遠小于防護樁使用的鋼筋和混凝土抗拉強度和抗壓強度,故判定防護樁安全。為對比與極限平衡計算的結果,圖13為基于數值模擬的樁側土壓力分布,對比圖3和圖13可知,兩種方法得到的土壓力分布較為接近,從而相互驗證了兩種方法的可靠性。

圖10 最小主應力

圖11 位移云圖
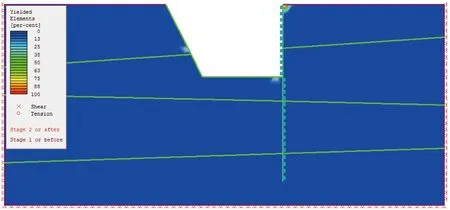
圖12 塑性區分布

圖13 樁側土壓力分布
4 結論
(1)基于郎肯土壓力計算方法,考慮樁前被動土壓力和樁背主動土壓力的力矩平衡條件,得到鉆孔樁
的安全嵌入深度為11.52 m。
(2)采用有限元數值模擬方法建立了基坑支護系統的地質力學模型,坑底隆起變形和坑壁側向變形隨著嵌入深度的增大而不斷降低,表明增大嵌入深度可以有效約束基坑的變形,但當嵌入深度增大到一定深度后,基坑變形不再受嵌入深度的影響,數值分析表明,最優嵌入深度約等于1.33倍基坑深度。

