二維過渡金屬硫化物二次諧波: 材料表征、信號調控及增強*

曾周曉松 王笑? 潘安練

1) (湖南大學物理與微電子科學學院, 微納結構物理與應用技術湖南省重點實驗室, 長沙 410082)

2) (湖南大學材料科學與工程學院, 化學生物傳感與計量學國家重點實驗室, 微納結構物理與應用技術湖南省重點實驗室, 長沙 410082)

二維過渡金屬硫化物(transition metal dichalcogenides, TMDCs)由于可實現從間接帶隙到直接帶隙半導體的轉變, 能帶寬度涵蓋可見光到紅外波段, 及二維限域所帶來的優異光電特性, 在集成光子以及光電器件領域受到了廣泛的關注. 最近隨著二維材料基礎非線性光學研究的深入, 二維TMDCs 也展現出了在非線性光學器件應用上的巨大潛能. 本綜述聚焦于二維層狀TMDCs 中關于二次諧波的研究工作. 首先簡述一些基本的非線性光學定則, 然后討論二維TMDCs 中原子層數、偏振、激子共振、能谷等相關的二次諧波特性.之后將回顧這些材料二次諧波信號的調制及增強工作, 討論外加電場、應變、表面等離激元結構、納米微腔等方法和手段的影響機理. 最后進行總結和對未來本領域工作的展望. 理解二維TMDCs 二次諧波的產生機制及材料自身結構與外場調控機理, 將對未來超薄的二維非線性光學器件的發展產生深遠的意義.

1 引 言

自從2004 年單層石墨烯被成功剝離以來, 二維層狀材料(two dimensional layered materials,2DLMs)作為一種單原子層的納米材料受到了極大的關注. 石墨烯展現出了較大的載流子遷移率與良好的韌性等一系列優異性質, 許多基于石墨烯的應用如光電探測器、鋰離子電池、超級電容等被設計出來[1,2]. 然而, 石墨烯表現出零帶隙和半金屬特性, 限制了其在光電領域的應用[3]. 因此尋找一種天然的類石墨烯的二維半導體材料成為了新的研究熱點. 此時, 以過渡金屬硫化物(transition metal dichalcogenides, TMDCs)為代表的二維層狀半導體材料進入了研究者的視野[4,5]. 這些二維半導體材料層間通過范德瓦耳斯力相結合, 除了擁有良好的電學性質以外[6,7], 它們還展現出了獨特的光學特性, 比如從可見光到太赫茲波段的寬帶光響應[8?10], 室溫下較大的激子結合能[11], 以及存在光學的各向異性[12]. 此外, TMDCs 還展現出許多層數依賴的光學現象. 當它們的厚度從塊體逐漸降低到單層時, 由于減小的介電屏蔽效應, 它們通常由間接帶隙半導體轉變為直接帶隙半導體[13]并且擁有打破的反演對稱性[14]. 由于自旋-軌道耦合,TMDCs 產生新的能谷自由度并且展現出能谷相關的圓偏振光選擇吸收效應[15]. 在非線性光學方面, 層數的變化使得它們展現出更多層數依賴的非線性光學效應, 比如隨奇偶層數振蕩的二次諧波強度[16]. 相對于傳統的半導體納米材料, 二維材料也展現出更大的非線性極化率, 因此它們在非線性光學領域有著天然的優勢.

非線性光學是研究材料在強相干光相互作用下產生的非線性效應及應用, 在激光技術、光通信和集成光學等多個領域得到廣泛應用. 比如飽和性吸收效應, 它來源于材料在高功率激發光作用下產生的對于激發光完全透過的現象, 對于具有這一特性的材料, 稱之為可飽和吸收體(saturable absorber, SA)[17,18]. 利用飽和吸收體, 一系列的超短脈沖激光器被研究制成[19,20], 為光通信領域奠定了重要基礎. 另外一類重要的非線性光學效應稱為諧波效應, 比如二次諧波(second harmonic generation,SHG)、 三 次 諧 波(third harmonic generation,THG)以及高次諧波(high harmonic generation,HHG), 它們來自于材料對基頻光場的不同階次的非線性極化. 其中在二(三)次諧波的過程中, 兩(三)個頻率為w的光子與非線性光學材料相互作用, 輻射出一個頻率為2w(3w)的光子. 二次諧波是最基本的二階非線性光學過程之一, 它涵蓋從高分辨生物成像[21]、探測晶體結構[22]、倍頻晶體[23]到非線性光學器件[24]等一系列應用. 二次諧波用于表征晶體結構時, 作為一種全光學的表征手段,對材料的形貌沒有要求, 在測試過程中也不會破壞材料結構, 對于難以進行透射電子顯微鏡表征的樣品是一種優秀的備用手段. 傳統用于產生二次諧波的倍頻晶體材料如b相偏硼酸鋇晶體(b-BaB2O4,BBO)、鈮酸鋰(LiNbO3)、鈦酸鋇(BaTiO3)或石英等通常是塊體材料, 不易用于小型化和可集成化器件. 近年來二維半導體展現出了較大的非線性光學強度以及獨特的非線性光學特點, 在非線性光學領域引起了廣泛的關注并取得了一系列重要的研究成果[25]. 二維材料非線性光學的進一步研究與發展有望滿足目前新型超薄非線性器件小型化、多功能、低損耗等的需求.

本文將回顧近年來二維材料在二次諧波領域相關的一些工作. 第2 節首先簡述一些非線性光學定則, 討論二次諧波產生的基本條件. 第3 節將討論二維TMDCs 中二次諧波相關的一些特性, 包括層數依賴效應、偏振效應、激子共振以及能谷選擇效應. 其中部分化學氣相沉積方法生長的材料擁有獨特的打破反演對稱性的結構使得它們產生增強的二次諧波效應, 展現了巨大的應用潛力. 第4 節和第5 節將回顧二次諧波信號在二維材料中的調制及增強工作. 其中外加電場、應變、表面等離激元結構、納米微腔等方法將會被討論. 最后對二維材料二次諧波的工作進行總結并展望未來可能的研究方向.

2 二次諧波相關的非線性光學定則

光與物質相互作用, 產生電極化強度P(t). 當施加光場為強激光時,P(t)可展開為光場強度E(t)的冪函數:

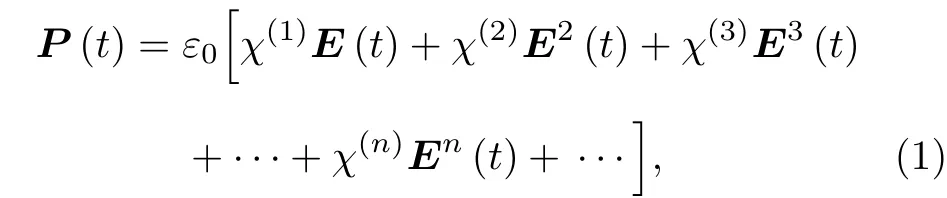
式中,e0為真空介電系數;c為極化率;c(1)為線性極化率, 用來描述傳統的線性光學效應;c(2)為二階非線性極化率, 描述二階的非線性過程. 在非線性光學的研究中, 當材料的非線性光學極化率足夠大時, 高階的非線性光學作用則變得重要. 前面已經提到過, 二次諧波是最簡單的二階非線性過程,接下來通過耦合波動方程, 將討論二次諧波過程中滿足的一些最基本的非線性光學定則.

首先寫出在非磁非導電無自由電荷的色散介質中傳播光場的波動方程(此時假定光波是平面波且為橫電波):

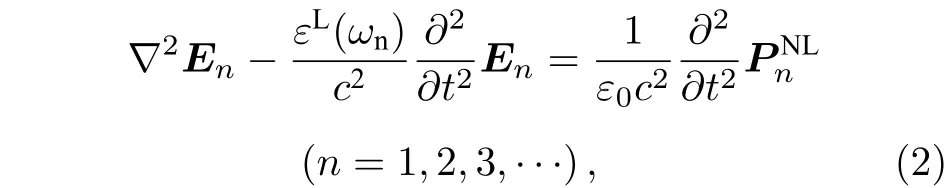
其中,En代表不同頻率wn光場的電場強度,εL(ωn)是不同頻率wn下線性極化的復介電常數,是不同頻率wn下的非線性極化強度, 它們都是位移r和時間t的函數,是真空中的光速,μ0為真空磁導率. 為了定量分析二次諧波過程中基頻光與倍頻光的相互作用與結果, 假設入射光場E1的頻率為w1, 經過長為L的非線性介質后, 出射倍頻光場E2的頻率為w2, 且為了簡化此時認為入射光場與出射光場延z方向共線傳播, 并令w1=w,w2= 2w, 那么此時出射(入射)光場可以寫為

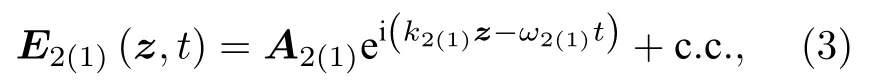
其中,k2(1)是出射(入射)光場波矢的絕對值,A2(1)是出射(入射)光場復振幅, 它是位移z的函數.將(3)式代入波動方程(2), 只考慮z方向的作用,在緩變振幅近似下, 二次諧波的耦合波方程為

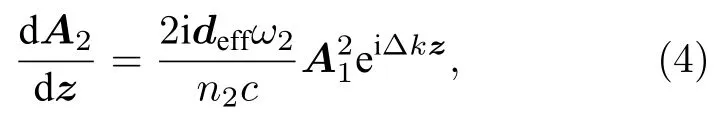
其中,ni是介質的折射率, Dk= 2k1–k2,deff=1/2c(2)為有效二階非線性系數. (4)式是入射光場與出射光場延z軸共線傳播的二次諧波耦合波方程, 假如此時認為二次諧波的轉化效率較低, 入射光場只有少部分能量轉化給出射的倍頻光場, 亦即認為入射光場的振幅不變為常數, 那么可以得到出射光場振幅隨傳播距離的變化情況:

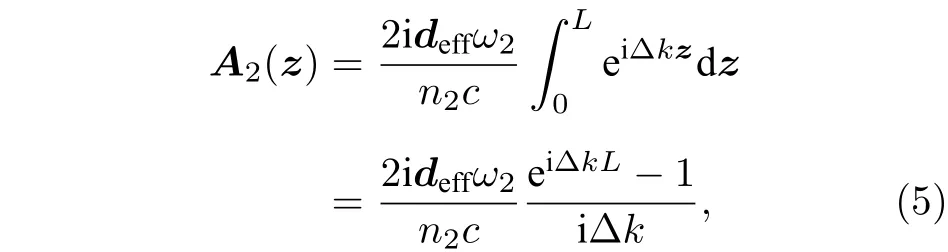
以及倍頻效率：

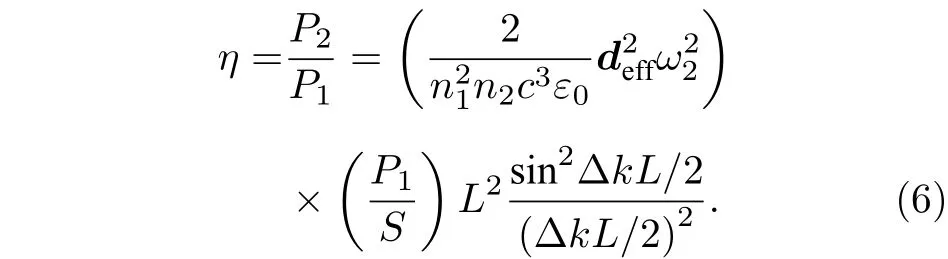
其中,Pn為光功率,P=IS(S為光束截面),I為光強,I= 1/2e0cn|A|2.

根據(6)式二次諧波的倍頻效率來討論二次諧波的產生情況. 首先討論二次諧波產生的相位匹配條件. 當Dk= 0 時, (6)式倍頻效率中的最后一項有極大值:

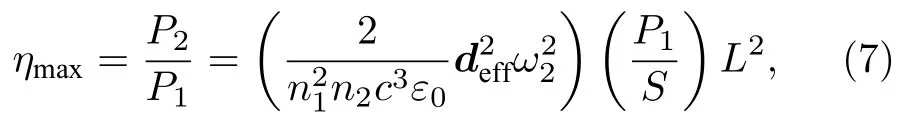
此時要求2k1=k2, 而根據波矢k公式ki=niwi/c和相速度公式ni=c/ni, 因此要求n1(w1) =n2(w2),也就是相位匹配的條件為材料在倍頻的折射率等于入射基頻的折射率. 而對于其他的波矢條件, 二次諧波的轉化效率會迅速衰減.

在相位匹配的條件下, (6)式二次諧波的轉化效率與入射光場和非線性介質的作用長度L的平方成正比. 而當Dk≠ 0 時, 稱為相位失配, 此時當DkL/2 =nπ (其中n為 ± 1, ± 2, ···)時, 轉化效率h有最小值為0, 而當DkL/2 =nπ/2 (其中n為± 1, ± 3, ± 5, ···)時,h極大值正比于4/(Dk)2.因此相位失配時, 二次諧波的轉化效率隨非線性介質的作用長度L呈振蕩趨勢.

另外, 二次諧波的產生對非線性介質的晶體結構非常敏感, 它要求晶體存在中心反演對稱性的打破. 對于中心對稱的晶體, 假如反轉晶體(此時考慮為反轉實驗室坐標軸):

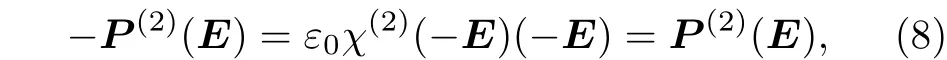
此時產生的極化強度P與電場E應該都與反轉前相反, 而計算出的電極化強度P不變, 因此中心對稱晶體的二階非線性系數c(2)= 0.

根據不同的材料體系, 二次諧波還展現出偏振的特性. 為了獲得偏振的二次諧波, 將二次諧波的電場方向表示為材料二階非線性系數以及入射電場的函數[16]:

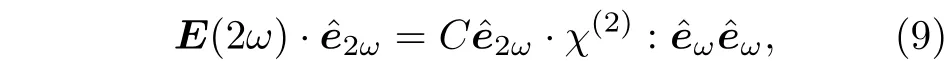
同時考慮到二次諧波的強度ISHG是電場強度的平方, 那么(9)式將演變為[26]

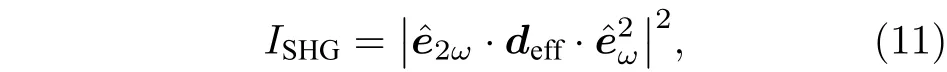
以上簡單討論了二次諧波產生的相位匹配條件, 隨非線性介質長度的變化情況以及偏振情況等, 下面將在二維材料中具體討論二次諧波產生的情況, 并且將看到在特殊的二維TMDCs 體系中,二次諧波的產生條件及特性將會強烈地受到材料性質的影響.

3 二維TMDCs 中的二次諧波現象

層狀的TMDCs 主要可以通過機械剝離和化學氣相沉積(chemical vapor deposition, CVD)生長獲得. 它們通常可以用結構式MX2表示, 其中M代表過渡金屬原子(如Mo, W),X代表硫族原子(如S, Se, Te). 單層TMDCs 結構上兩個硫族原子像三明治一樣上下夾住一個過渡金屬原子構成, 層間由范德瓦耳斯力相結合(圖1(a)). 典型的TMDCs 如二硫化鉬(MoS2)、二硫化鎢(WS2)單層約0.7 nm, 當厚度從塊體降低到單層時, 它們由間接帶隙轉變為直接帶隙, 并且逐漸產生較強二次諧波信號[14]. 在傳統機械剝離的二維TMDCs 中,二次諧波展現出奇偶層數依賴效應、偏振效應、激子共振效應以及能谷選擇效應等.

3.1 層數依賴

2013 年, Malard 等[16], Kumar 等[27]以及Zeng等[28]3 個研究組報道, 不同于塊體材料, 當MoS2(WS2)的層數減小到單層時, 他們觀察到了非常強的二次諧波效應(單層MoS2中二階非線性系數c(2)約0.6 nm/V[16], 單層WS2中約0.5 nm/V[29]),這種現象來自于單層時反演對稱性的打破. 通常來說機械剝離的二維TMDCs 是2H (2-hexagonal)相, 這使得它們在奇數層時存在反演對稱性的打破而偶數層反演對稱性的恢復, 因此最終出現奇數層存在二次諧波而偶數層二次諧波的信號消失的現象(圖1(b)和圖1(c)). 當層數緩慢增加至5—7 層時, 奇數層MoS2也會出現二次諧波信號迅速遞減的趨勢. 這種現象可以理解為每一個奇數層是底部單層與上部分偶數層二次諧波信號的疊加, 當層數增加時, 上面的偶數層不貢獻信號反對底部單層產生的二次諧波信號吸收增加, 使得總的信號減小.所以最終隨著層數的增加, MoS2的二次諧波信號呈現出振蕩減小的趨勢, 最終形成塊體時非線性極化率c(2)只有10–14m/V[30].

盡管在以MoS2為代表的少層二維TMDCs材料中能夠探測到較強的二次諧波信號, 單層的TMDCs 因為其單原子層薄的特點, 與激發光的作用截面十分有限, 導致其二階非線性極化率c(2)較小, 產生二次諧波信號在應用上依然面臨挑戰. 因此想要二維材料在非線性光學器件中得到應用, 還需要能夠高效產生二次諧波的二維層狀材料.

圖1 (a) MoS2 原子排列的側視圖(左)和俯視圖(右), 其中俯視圖中對應扶手椅和Z 字形兩個晶體取向; (b) 機械剝離方法得到的不同層數MoS2 的光學照片[16]; (c) 2H 相MoS2 二次諧波信號隨層數增加呈振蕩減小的趨勢[16]; (d)人工折疊的兩層MoS2(左)以及對應的二次諧波成像(右)[31]; (e) 3R 相MoS2 晶體結構及倍頻偶極排列[32]; (f) 3R 相MoS2 二次諧波呈平方遞增的趨勢[32]Fig. 1. (a) Side view (left) and top view (right) of MoS2 atomic structure. The highlighted armchair direction and zigzag direction correspond to the top view. (b) Mechanical exfoliated MoS2 with different layers[16]. (c) 2H phase MoS2 layers show diminishing the oscillation in SHG signal[16]. (d) Optical image of artificial folded MoS2 (left) and its corresponding SHG image(right)[31]. (e) Crystal structure of 3R phase MoS2 and corresponding SH dipole[32]. (f) 3R phase MoS2 layers show quadratic enhanced SHG with the increase of layers[32].

不同于直接剝離得到兩層的MoS2, 復旦大學的Jiang 等[31]將單層的MoS2折疊, 得到了多種不同堆垛結構的兩層MoS2. 在圖1(d)中, 左側的a,b, c 三個區域都是由單層MoS2通過人工折疊形成的兩層MoS2區域. 在右側對應的二次諧波成像中可看到, a 區域表現出二次諧波信號的消失, 這與直接機械剝離獲得的兩層MoS2情況相同, 因為偶數層存在反演對稱性的恢復. 但是b 區域與c 區域相對于單層, 呈現出增強的二次諧波信號, 這表明它們依然存在打破的反演對稱性, 并且層數的增加使對稱性破缺更加明顯. 單層的MoS2中存在兩個晶體取向, 分別為扶手椅(armchair)晶向和Z 字形(zigzag)晶向, 見圖1(a). 如果單層的MoS2沿著Z 字形晶向折疊, 那么形成的雙層MoS2類似于天然的2H 相兩層MoS2, 不存在反演對稱性的打破, 稱之為2H-like 結構, 圖1(d)中a 區域就是這樣. 如果單層的MoS2沿著扶手椅晶向折疊, 那么第二層的Mo 原子將處于第一層Mo 原子的正上方, 第二層的MoS2的原子排列相對于第一層完全重復, 因此將打破反演對稱性從而產生增強的二次諧波信號. 這種結構稱之為3R-like 結構, 圖1(d)中b 區域就屬于這種情況. 如果折疊的晶向既不平行于Z 字形晶向又不平行于扶手椅晶向, 那么得到的兩層MoS2結構也不存在反演對稱性, 因此圖1(d)中c 區域也會出現二次諧波信號. 對于b 區域這種特殊的情況, 加州大學伯利克分校的Zhao 等[32]進行了進一步的研究. 通過化學氣相運輸(chemical vapor transport, CVT)的方法, 他們直接生長出了3R (3-rhombohedral)相的MoS2晶體, 并通過機械剝離的方式得到了少層的MoS2納米片. 圖1(e)是3R 相MoS2的原子排列以及其產生二次諧波偶極矩的疊加情況. 可以看出與Jiang等[31]折疊形成的結構稍有不同, 自然的3R 相結構可以看作每一層為單層MoS2在垂直方向上的復制并在面內產生一定的平移(而不是處于每一層的正上方), 這符合能量最低的原理. 同時這種原子結構每一層產生倍頻偶極取向都相同, 因此保證了層與層間存在增強的疊加效應. 通過表征不同層數的3R 相MoS2, 最終發現隨著層數的增加二次諧波信號與層數呈平方遞增的關系, 并且這種關系直到十層也僅僅因為吸收的原因而減弱20%.

這種不同原子堆垛導致反演對稱性破缺從而產生二次諧波差異性的情況常常被用來分辨不同晶相的二維材料. 湖南大學的Zeng 等[33]以及華中科技大學的Yang 等[34]分別合成了2H, 3R 相的WS2、二硒化鎢(WSe2)以及二碲化鉬原子晶體,并且借助二次諧波的表征區分了不同相的沉積溫區, 實現了大面積3R 相的可控合成. 西北工業大學的Song 等[35]對比了半導體2H 相和半金屬1T'(monoclinic)相二碲化鉬, 發現1T'相二碲化鉬二次諧波轉化效率極大降低, 且轉變為點群, 展現出不同的偏振特性. 加州大學伯克利分校的Wang等[36]通過靜電摻雜實現了單層二碲化鉬2H 相到1T'相的轉變, 偏振的二次諧波測試表明相變后的1T'相二碲化鉬依然保持原2H 相的晶體取向. 深圳大學的Hao 等[37]可控合成了e相的硒化銦(InSe)、碲硒化銦(InSe1–xTex)以及硫硒化銦(InSe1–xSx)原子晶體, 并且展現出相比于普通2H相TMDCs 高一到兩個量級的二階非線性系數.

利用化學氣相沉積的方法, 還能可控合成具有特殊結構的二維材料. 化學氣相沉積法利用含過渡金屬原子以及硫族原子的化合物作為目標材料的前驅體在高溫進行反應并沉積生長在硅片上, 這個過程中通常受到溫度、流速、過飽和度等因素的影響[38], 因此合成出的二維材料可以擁有特殊打破反演對稱性的結構. 利用這種方法設計生長新型的二維材料, 能夠產生高效的二次諧波.

湖南大學的潘安練課題組[39,40]可控合成了在形貌結構上產生對稱性破缺的螺旋結構WS2, 展現出增強二次諧波的同時解釋了其生長的機理.圖2(a)是螺旋WS2的光學圖片, 螺旋WS2通過高溫的化學氣相沉積方法直接生長在鍍有二氧化硅的硅片上. 圖2(a)中右圖是左圖光學照片樣品中心處的原子力顯微鏡(atomic force microscopy,AFM)表征, AFM 掃描成像清晰地顯示出WS2中心的螺旋結構. 這種螺旋結構由獨立的單層通過螺位錯螺旋生長而來, 螺位錯的引入是因為沉積溫區存在不同的過飽和度. 它不僅使得生長的WS2具有獨特的形貌, 同時螺位錯的引入打破了層與層之間的對稱中心, 因此使得螺旋WS2的二次諧波強度隨層數遞增, 中心區域可達單層強度的上百倍(圖2(b)).

中國科學院化學研究所的Lin 等[41]報道合成了金字塔形的WS2(圖2(c)). 金字塔形的WS2每一層由不完全覆蓋的三角形單層WS2組成, 厚度可達一百多納米(200 多層), 這種獨特的結構通過在生長過程中逐漸減小載氣的流速獲得. 金字塔形的WS2層間是2H 相的堆垛結構, 因此它的二次諧波強度隨著厚度的增大最初表現為與2H 相類似的振蕩減小趨勢. 然而當層數增加到約70 層時,金字塔形的WS2表現出急劇的二次諧波信號強度增大. 這些二次諧波信號來自于材料殘存不完全覆蓋的邊緣. 金字塔形的WS2自身形成一個類似于回音壁模式的納米腔, 它將限域并放大邊緣產生的二次諧波信號, 最終相比單層可達40 倍的信號增強. 同時這種納米腔的特性還反映在波長依賴的二次諧波信號上, 通過改變腔長(即金字塔形WS2的大小), 二次諧波的強度能夠周期性的隨激發光的波長產生變化, 并且它的模式間隔滿足: Dl=l2/(nL) = 2l2/(3nD), 其中n是WS2反射系數,l是激發光的波長,D是金字塔形WS2的邊長.

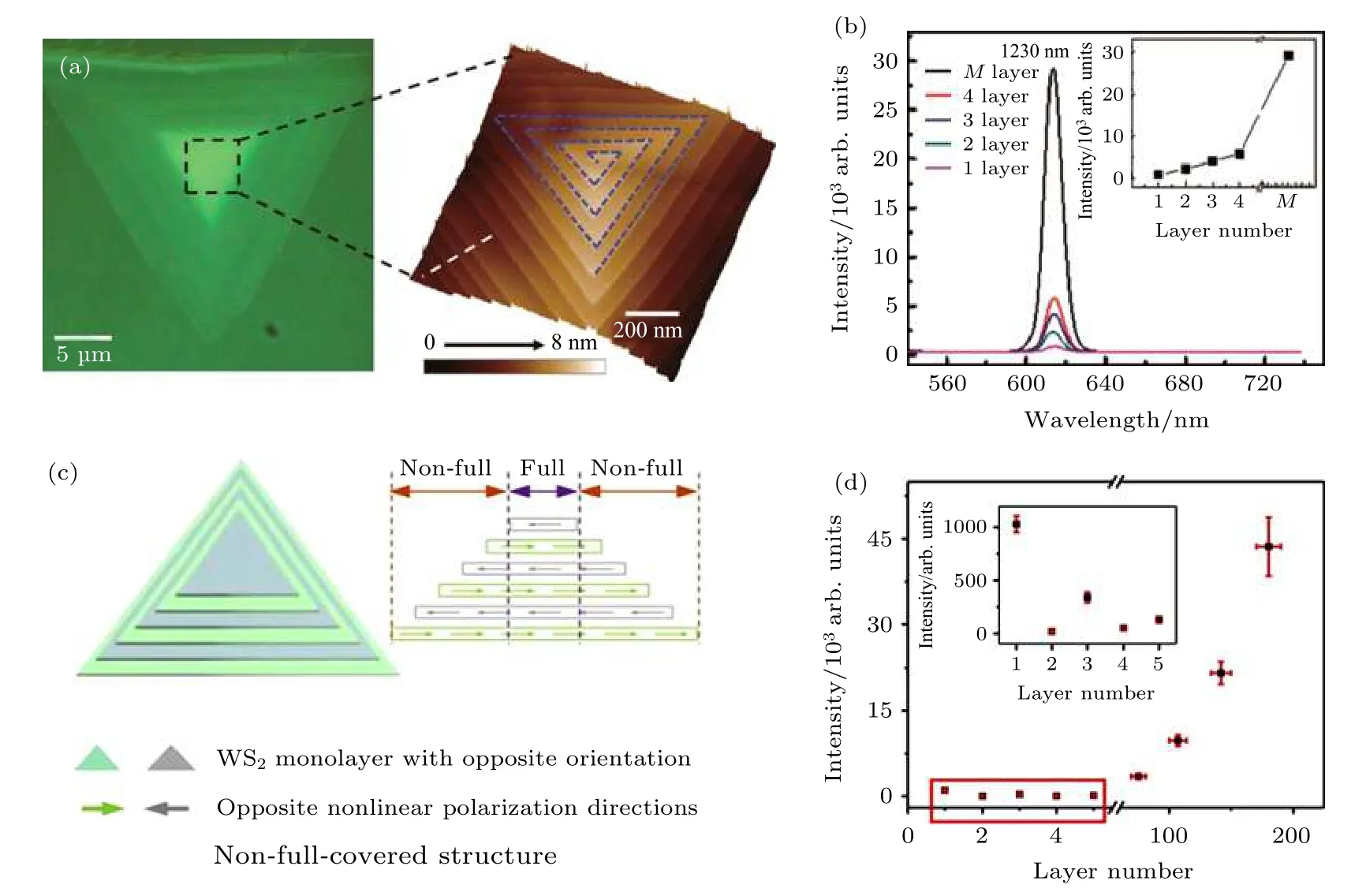
圖2 產生高效二次諧波的二維材料 (a)螺旋WS2 的光學照片及圖中虛線正方形區域內放大的螺旋WS2 樣品中心AFM 圖片[39]; (b)螺旋WS2 的二次諧波強度隨層數遞增[39]; (c) 金字塔結構的WS2 納米片結構示意圖[41]; (d)金字塔形的WS2 納米片邊緣形成高效二次諧波[41]Fig. 2. CVD grown TMDCs with highly efficient SHG: (a) Optical image (left) and zoom in AFM image (right) of spiral WS2 flake[39]; (b) layer dependent SHG of spiral WS2 flake[39]; (c) schematic illustration of pyramid-like WS2 structure[41]; (d) pyramid-like WS2 displays high intensity of residual edge SHG signal[41].

利用化學氣相沉積生長的這些具有高對稱性破缺的二維TMDCs 在一定程度上彌補了2H 相機械剝離二維材料光物質相互作用截面小, 二次諧波效率低的劣勢, 根據計算它們的二次諧波轉化效率已能夠匹敵現今商業化的BBO 倍頻晶體[39], 這也為將來超薄非線性倍頻器件的應用打下了基礎.

3.2 偏振特性

二次諧波作為表征手段其中最重要的一種作用是可以通過偏振的測試反映材料的晶體取向, 二次諧波的偏振檢測手段也作為一種全光學無損的手段廣泛地應用于各種材料體系[22,42,43]. 前面提到過, 二次諧波的偏振方向由入射電場的方向以及材料的有效二階非線性系數deff決定. 在2H 相二維材料中, 奇數層結構屬于D3h點群, 通過晶體對稱性的簡化, 它的有效二階非線性系數矩陣為

其中,d21=d16= –d22. 根據(11)式, 若入射光垂直入射到樣品上并將入射電場投影到樣品的扶手椅方向上, 2H 相TMDCs 中平行和垂直的二次諧波可以寫為[16,26]

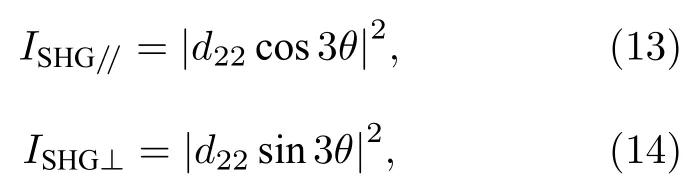
其中,q角定義為入射光電場方向與樣品扶手椅方向的夾角(圖3(b)). 因此2H 相TMDCs 中偏振的二次諧波極化圖展現出六瓣花瓣的形狀(圖3(a)),每個花瓣(即二次諧波的最大值)對應于樣品的扶手椅晶向, 這種六倍的旋轉對稱性也符合D3h點群結構. 對于未知晶體取向的樣品, 也可以通過偏振的二次諧波測定樣品的晶體取向.

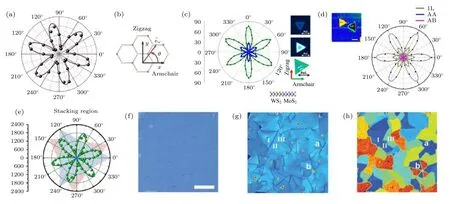
圖3 二次諧波的偏振特性 (a) 單層MoS2 的二次諧波偏振極化圖[16]; (b)單層MoS2 晶體取向俯視圖, 其中x 方向代表扶手椅方向, y 方向代表Z 字形方向, q 角是激發光入射方向與扶手椅方向的夾角[16]; (c) WS2/MoS2 橫向外延異質結[44]以及(d) WSe2/WS2 AA 和AB 堆垛結構縱向外延異質結[45]的二次諧波偏振極化圖, 其中插圖是異質結的二次諧波成像; (e) 人工堆垛兩種二維材料使二次諧波極化方向產生疊加[46]; (f)—(h)利用二次諧波偏振區分單層MoS2 中不同晶界與疇界[47]Fig. 3. Polarization properties of SHG in TMDCs: (a) SHG polarization in monolayer MoS2 shows six fold rotation symmetry[16]; (b) top view of MoS2 crystallographic orientation, where x represents armchair direction, y represents zigzag direction and q is the angle between input laser and armchair direction [16]; SHG polarization in (c) WS2/MoS2 laterally epitaxial heterostructure[44] and (d) WSe2/WS2 AA, AB vertical heterostructure[45], where the insets shows correspongding SHG mapping; (e) superposition of SHG polarization by artificial stacks of two different 2D materials[46]; (f)?(h) demonstration of distinguishing of different grain boundary in monolayer MoS2 thin film be SHG polarization[47].

清華大學的Zhang 等[44], 以及湖南大學的Wu 等[45]通過化學氣相沉積的方法分別可控生長了橫向外延的WS2/MoS2, WSe2/ MoSe2, 以及縱向外延的WSe2/WS2異質結. 在Zhang 等[44]的實驗中, 中間的鎢原子結構TMDCs 與外延的鉬原子TMDCs 展現出相同的六倍旋轉對稱極化圖像,且極化圖的最大值取向相同(圖3(c)), 這證明生長的異質結結構沒有受晶格失配的影響, 橫向外延異質結的異質界面是兩種材料的Z 字形晶向; 而在Wu 等[45]的實驗中, 同樣的極化現象出現在底層的WS2以及頂層的WSe2上(圖3(d)), 證明垂直結構的異質結呈完美的AA 和AB 堆垛.

2014 年, Hsu 等[46]通過濕法化學轉移了兩種不同二維材料得到了不同堆垛角度的雙層結構, 并且在偏振的二次諧波表征中發現一個明顯的疊加規律. 通常來說, 化學氣相沉積生長的三角形形狀的二維材料扶手椅方向對應于三角形高的方向,而Z 字形方向對應于三角形邊的方向. Hsu 等[46]首先通過偏振確定了兩種單層的MoS2晶體取向與極化方向, 然后將它們堆疊成任意角度的兩層.在能夠獲得二次諧波的兩層樣品中(即堆垛角不等于60°), 發現兩層MoS2的二次諧波偏振依然表現為六瓣的旋轉對稱, 但是花瓣的位置(即極化最強的方向)出現在兩層MoS2三角形疊加角的平分線上. 通過大量的不同二維材料疊加二次諧波偏振測試, 總結出了兩層二維材料任意角度堆垛時二次諧波極化的疊加方向:

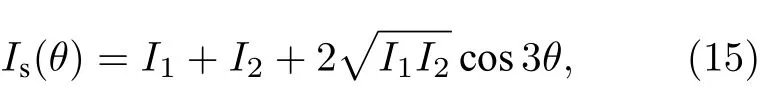
其中,I1,I2和Is分別為第一層、第二層以及堆垛區域總的二維材料二次諧波強度;q是堆垛角, 它代表兩個三角形二維材料最臨近的兩個角(屬于不同的兩層)的垂直平分線所夾的角度(圖3(e)的極化圖中即為紅色與藍色三角形垂直平分線所夾的最小的角度). 對于q= 60°的情況, 此時可以看作一個完全的2H 相堆垛導致了兩層疊加后二次諧波完全抵消, 而對于q= 0°的情況可以看作3R相堆垛導致疊加區域的二次諧波強度翻倍. 因此二次諧波極化的偏振可以看成兩層材料二次諧波極化方向的矢量疊加. 理解基本的二維材料二次諧波疊加規律對后續研究者的調制工作有著非常重要的意義.

利用偏振的二次諧波檢測手段還可有效地分辨出單層多晶二維材料的晶界取向. 圖3(f)—(h)是Yin 等[47]報道的在單層MoS2上通過二次諧波偏振的成像將看似均勻的薄膜區分出不同的疇界區域. 圖3(f)是一個大面積的單層MoS2薄膜, 其尺寸可達上百微米, 在光學顯微鏡的觀察下, 薄膜展現出良好的均勻性, 只能看出上面存在許多成核的位點. 二次諧波的成像(圖3(g))則展現出了更加豐富的信息, 整個單層的MoS2薄膜雖然擁有相對均勻的二次諧波信號, 但是它卻是由許多20—40 μm 單晶疇界組合形成的多晶. 在疇界交界的區域, 由于相鄰邊界取向不同, 它們或疊加增強或相干相消, 因此展現出明顯的晶界. 在早期透射電鏡的表征中, 晶界被觀察到是只有幾個原子尺度寬的狹窄區域[48], 但是在二次諧波的成像中卻清晰地呈現為一條條黑線把相鄰的疇界隔開. 由于MoS2三倍旋轉對稱的晶體結構, 單純的二次諧波成像并不包含相位信息, 因此不能區分出相反的晶體取向, 此時二次諧波的偏振則能夠進一步挖掘內部存在的信息. 根據上面的推導結論:ISHG//=|d22cos 3θ|2,ISHG⊥=|d22sin 3θ|2, 如果將同一個單層薄膜區域分別進行平行和垂直的二次諧波偏振表征, 那么就能反過來計算出不同疇界之間的晶體取向:

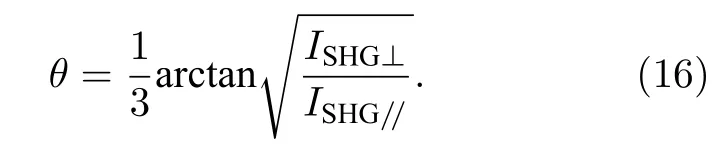
結合二次諧波成像以及偏振的信息就能得到完整的晶體取向. 例如, 在圖3(h)色彩取向圖中Ⅰ與Ⅱ區域, 雖然呈現出相同的顏色, 但是通過圖3(g)二次諧波成像可以看出Ⅰ與Ⅱ區域間存在明顯的晶界, 因此這兩個疇界存在完全相反的晶體取向;而圖3(f)中Ⅱ與Ⅲ區域在二次諧波的成像中表現出近乎相同的顏色襯度, 但是經過偏振的二次諧波計算后, 它們在色彩取向圖3(h)中展現出晶體取向差異約12°.

3.3 激子共振特性

二維TMDCs 的二次諧波還展現出激發波長依賴的激子共振特性. 由于二維材料在垂直方向上只有一個或幾個原子層的厚度, 因此在這個方向上它們表現出非常強的量子限域的效應以及減小的靜電屏蔽作用, 且因為庫侖相互作用產生激子. 激子是一種電子空穴對, 通常由于結合能較小在室溫下會被解離. 而單層MoS2的厚度約0.7 nm 小于激子的玻爾半徑(約0.93 nm), 這使得它擁有非常大的激子結合能并形成穩定的萬尼爾激子(Wannier exciton)[11]. 另外在MoS2和WS2中, 由于價帶的劈裂還會形成A 和B 兩種不同類型的激子, 它們的存在早先也都通過理論與實驗得到驗證[49]. 為了確定二次諧波與激子直接的關系, 法國圖盧茲大學的Wang 等[50]在4 K 的低溫下進行了激發光波長依賴的二次諧波測試. 他們發現當倍頻信號的能量與WSe2的1s 態A 激子以及1s 態的B 激子共振時, 最大將會產生三個量級增強的二次諧波信號. 而雙光子熒光激發的實驗中, 這種增強的現象并沒有出現. 因此他們認為除了電偶極矩耦合光物質相互作用外, 還存在一些其他的因素影響二維材料中的二次諧波信號產生, 并且他們將這種因素解釋為激子效應. 上面提到過, 二次諧波的產生是通過基態吸收兩個相同頻率為w的光子到虛擬態, 輻射出一個頻率為2w的光子. 其中, 在這個過程中沒有電子轉移的出現, 稱為參量過程. 在激子共振的情況下, 二次諧波的產生可以利用能量相近激子態作為中間態. 激子態是一個實態, 相比于二次諧波過程的中間虛擬態, 它擁有更長的壽命,這將極大地增強二次諧波產生的效率, 因此在二次諧波能量與激子能量發生共振時, 會產生數量級程度的增強. 這種激子共振的效應也被紐約哥倫比亞大學的Malard 等[16]所觀測到. 在圖4(c)中,單層(深藍)與三層(綠)的MoS2展現出的吸收峰(實線)中可以明顯看到在布里淵區K點形成的A 和B 激子以及G形成的C 激子, 并且由于能帶排列的原因它們的峰位稍有偏移. 在波長依賴的二次諧波(散點)信號中, C 激子共振的波長出現了明顯的增強并且同樣的偏移也反映在了其中.

在化學氣相生長的樣品中, 由于材料結構的不均勻, 摻雜元素的不同或邊緣效應, 激子共振的特性還會受到能帶或能態的影響. 2020 年湖南大學Fan 等[51]報道, 在化學氣相生長的螺旋結構WS2中, 他們觀察到了除激子共振外, 還存在激發光能量稍高于電學帶隙時的二次諧波增強(圖4(e)).2016 年, 韓國蔚山大學的Le 等[52]合成了單層不同組分的硒硫化鉬三元合金, 并且研究了硒摻雜對二次諧波的影響. 如圖4(f)所示, 從下到上是增加硒原子含量后從純的MoS2調控為硒硫化鉬合金再變成純的MoSe2時不同組分的二次諧波光譜(散點)與熒光(曲線)光譜. 可以看出, 隨著硒原子含量的增加, 共振的二次諧波光譜呈紅移趨勢, 并且表現出相對A 激子更加明顯的B 激子共振. 當硒硫化鉬MoS2(1–x)Se2x中x的組分為 0.18 和 0.3 時,B 激子附近的二次諧波強度慢慢接近A 激子的強度, 而當x= 0.62 時, B 激子共振的二次諧波強度已經是A 激子的兩倍. 實際上這種B 激子共振在純的二硫(硒)化鉬中是被抑制的. 對于這種二次諧波共振擴寬的現象, Le 等[52]通過合金樣品的能態改變進行了解釋. 在硒硫化鉬合金樣品的合成過程中, 隨機的硒原子替換會導致局部的電子結構發生改變, 這種現象已經通過掃描隧道顯微鏡被觀察到[53]. 同時這種能態的拓寬也反映在隨樣品紅移逐漸拓寬的熒光光譜半高寬上. 因此激子共振和缺陷態的拓寬共同造成了B 激子共振的增強, 且隨著硒元素的摻雜, 合金樣品的二階非線性系數逐漸增大, 這對于調控高效的非線性光學材料同樣提供了新的思路.

2014 年加州大學伯利克分校的Yin 等[47]報道了一種邊緣效應導致的獨特二次諧波共振現象.在大面積生長的單層MoS2中, Yin 等用稍高于兩倍A 激子共振的波長(0.93—0.97 eV)對其進行二次諧波成像, 可以看出在一些特定的波長下, 單層材料邊緣由于邊緣態共振, 實現了二次諧波信號增強(圖4(g)—(h)). 這一現象被臺灣成功大學的Lin 等[54]做了進一步的研究. 通過球差透射電子顯微鏡的表征可以發現, 生長的單層MoS2存在兩種不同的截止邊(即三角形納米片的邊緣), 其中三角形邊緣稍微內凹的是硫截止邊, 而三角形邊緣更直的是硫-鉬Klein 截止邊(類似于石墨烯中的Klein 邊). 對于這兩種不同的截止邊, 通過計算發現它們存在不同的邊緣態對應不同的共振能量, 因此可以觀察到不同激發波長下不同的邊緣二次諧波增強效應[54].

3.4 能谷選擇特性

二維TMDCs 的另一個獨特的特點是其具有新的能谷自由度. 基于能谷自由度, 許多不同于其他納米材料新的物理現象被發現. 能谷是指布洛赫電子能帶的最高處或最低處, 二維材料的能谷極化特性簡單來說源于其布里淵區+K與–K點對于右圓(s+)光子與左圓(s–)光子的選擇性吸收[55]. 如果基于這種選擇特性對二維材料中非簡并的能谷進行調控, 那么就能形成分立的能谷自由度. 單光子的過程中, 二維的TMDCs 在低溫下展現出極大的谷極化率[56,57], 特別的WS2由于硫鎢鍵的原因在室溫下展現出超過20%的谷極化率[58], 這些現象對二維的谷邏輯器件鋪下了堅實的基礎. 同時,能谷的效應在雙光子過程中也有著重要的發現.2015 年Seyler 等[59]報道了A 激子共振時WSe2的二次諧波能夠產生近乎100%的圓偏振極化度.如圖5(a)所示, 當圓偏振的激發光與WSe2的A 激子共振時, 兩個基頻(w)的左圓(s–)光子將產生一個幾乎偏振一致的右圓(s+)倍頻(2w)光子,而右圓(s+)激發時情況正好相反. Seyler 等將這種現象解釋為單層WSe2由于D3h晶體結構存在反演對稱性的打破以及三倍的旋轉對稱, 使得晶格產生了角動量吸收與發射光子的不匹配. 通常來說, 在單光子的過程中, 二維材料的布里淵區的+K(–K)點只吸收s+(s–)的光子. 而對于雙光子的帶間轉移過程, 展現出了翻轉的選擇定則: 兩個s+(s–)光子可以被–K(+K)點同時吸收, 并輻射出相反的s–(s+)光子(圖5(b)). 這種二維材料中獨特的高偏振度的雙光子選擇定則在2015 年被Xiao 等[60]做了進一步的總結. 在二維材料光物質相互作用的過程中, 三倍的旋轉對稱要求材料保證總角動量守恒. 因此材料的能谷角動量 ?τ? , 激子角動量 ?l? , 晶格角動量 3N? 和光子自旋角動量?m?將滿足以下關系:

即雙光子吸收過程中, 自旋角動量的變化將引起能谷、激子以及晶格角動量的變化. 基于這個選擇定則, 雙光子過程如雙光子熒光與二次諧波都將展現出能谷-激子鎖定的效應, 也就是說在激子共振的情況下, 純的s–或s+激發都將只在確定的能谷中發生[60]. 例如, 在1s 態共振激發的WS2二次諧波中, +K谷基態到1s 態的轉移要求?1? 的能谷角動量變化以及 0? 的激子角動量變化, 因此這個過程只有通過吸收兩個純的帶有 2? 動量的s+光子,并輻射出剩余的 3? 角動量進入晶格. +K點的1s 態將輻射出s–的倍頻光子. 這個選擇定則將總結并歸納了共振的雙光子過程中, 圓偏振光激發允許以及禁止的躍遷態, 它對控制能谷光電器件的應用如光開關邏輯器件有著重要意義.

4 二次諧波信號調制

二維材料中二次諧波信號的可調制性源于二維材料自身受熱力光電產生的二階非線性系數的變化, 同時這也使得二維材料產生的二次諧波有了更為廣泛的應用. 基于各種調制下的二次諧波, 許多非線性光電器件被設計出來, 有望成為將來高效超薄低閾值非線性器件的基礎.

4.1 電調控二次諧波

電調控二次諧波(electric field-induced 2ndharmonic generation, EFISHG), 作為一種最為廣泛的調制手段之前在各種納米材料與結構中有著許多先例[61?63]. 電調控二次諧波最早在1962 年由方解石上施加一個很強的電場來打破其反演對稱性被觀測到[64]. 電調控二次諧波的基本原理可以認為是電場與三階非線性系數的相互作用, 即產生的有效的二階非線性系數為[65]

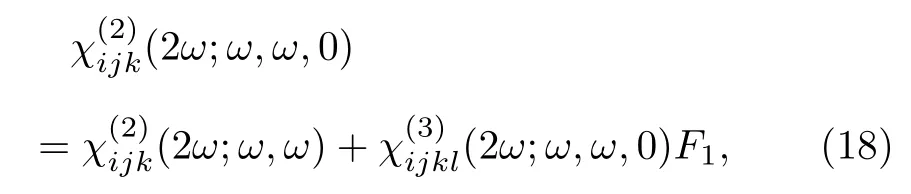
在二維材料中一個有趣的想法是能否通過施加電場打破2H 相兩層材料的反演對稱性產生二次諧波. 這個想法隨后便由Yu 等[66]以及Klein等[67]實現. 在2015 年和2017 年Yu 等以及Klein等分別通過施加垂直電場在二層WSe2以及MoS2中成功調制出了二次諧波信號. Klein 等的器件結構如圖6(a)所示, 雙層的二硫化鉬被夾在290 nm 的二氧化硅以及20 nm 三氧化二鋁的介電層之間, 然后在頂部的鈦/金電極與底部的n 摻雜硅上施加垂直電場, 整個器件沒有電流產生避免燒壞樣品. 首先在較低–20 V 的電壓下, Klein 等在MoS2C 激子共振的能量附近E= 2.75 eV, 將天然存在反演對稱性的雙層MoS2調制出了二次諧波信號, 并且產生的二次諧波在偏離C 激子的共振位置后有一個量級的衰弱, 這個現象可以由激子的共振效應解釋. 接下來他們將調制的二次諧波同時表征為電壓(–120 V ≤Vg≤ 120 V)與激發波長(Ew～1.25—1.47 eV)的函數(圖6(b)), 此時他們發現調制出的最大二次諧波出現在電壓為120 V, 能量為E2w–Ec= –0.26 eV 偏離C 激子共振的位置, 且最大調制出二次諧波信號為–20 V偏壓下的60 倍. 對于這種共振的偏移, Klein 等計算了外加電場對MoS2波函數的影響. 當正好與C 激子發生共振時, 外加電場對于MoS2布里淵區的G以及M點只有非常微弱的影響, 而當激發偏移C 激子能量一定值時, 布里淵區的S點發生了明顯的變化, 這是由于相對于C 激子共振的情況,外加電場使得其原子軌道耦合布洛赫態, 因此布里淵區展現出了更強的對稱性打破[67]. 類似的器件結構以及結果由Yu 等在雙層2H 相的WSe2中獲得. 它們在正負40 V 的垂直外加電場下將雙層的WSe2成功調制出了二次諧波信號, 但調制出的信號相比單層低了2 個數量級. 對于調制的機理, 與Klein 等不同, Yu 等認為是電荷導致的二次諧波(charge induced second harmonic generation,CHISHG), 并且他們用鍵電荷模型加以解釋[66]. 在這個模型中, 雙層WSe2中的硒離子與鎢離子由各自的鍵bn相連接, 它們的鍵電荷qn相對于鍵中心的移動導致了二階鍵超極化率, 而所有二階超極化率的疊加導致了整體的二階非線性極化率c(2). 如果考慮在單層的WSe2是由頂部和底部的硒原子連接中間三個相同的鎢原子, 施加向下的垂直電場后, 對于總的六個鍵都會導致鍵電荷q1—3向上移動. 但是對于單層中下半層的超極化率將會被削弱, 因為鍵電荷q1—3會向中間的鎢離子移動, 而上半層的鍵電荷q4—6會向硒離子移動, 因此使上半層的超極化率增強. 所以,總的二階非線性極化率c(2)不變, 而直流電場下EFISHG 理論對單層WSe2不存在調控, 因此不是EFISHG 理論使得雙層WSe2產生了二次諧波信號. 在Yu 等的CHISHG 理論中, 當垂直電場Vg的強度超過閾值時, 鎢的道上將形成空穴收集層, 并且它將作為屏蔽電荷層阻止電場進一步對穿透. 微觀上, 屏蔽的電場Vg與鍵電荷qn相互作用, 使得單層中底部半層的鍵電荷q1—3朝著中間的鎢原子移動, 而對于上半層的鍵電荷由于空穴收集層的屏蔽效應將不受到影響, 上下半層的超極化率不再相互抵消, 因此整個單層的二階非線性極化率c(2)將受到電場調控. 對于兩層的WSe2而言, 理論上還是會由于對稱的屏蔽效應而抵消補償. 但是實際上由于帶邊態的密度太大,整個空間的靜電荷會局域在底部的鎢原子面上. 簡單來說頂層鎢原子面的帶電量僅為底部的4%, 因此雙層WSe2的底部單層依然有很大一部分不受抵消, 因此二階非線性系數c(2)不為0, 它正比于垂直電場與閾值電壓差的絕對值|Vg?Vt|.

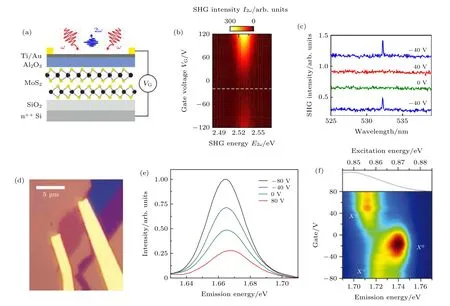
圖6 電調控二次諧波 (a) 雙層MoS2 微電容器件原理圖[67]; (b) 雙層MoS2 的二次諧波作為施加電壓以及發射波長的函數[67];(c) 雙層WSe2 中背柵調控可逆的二次諧波[66]; (d) 單層WSe2 晶體管的光學圖片[59]; (e) 單層WSe2 二次諧波在共振激發下隨選定柵壓的變化[59]; (f) 單層WSe2 二次諧波作為柵壓和激發能量函數的強度圖[59]Fig. 6. Electric field modulated SHG: (a) Schematic illustration of bilayer MoS2 microcapacitor device[67]; (b) bilayer MoS2 SHG intensity as the function of applied voltage and SHG emission energy[67]; (c) reversible SHG induced by back gate in bilayer WSe2[66];(d) optical image of monolayer WSe2 transistor[59]; (e) exciton resonant monolayer WSe2 SHG spectra at selected gate voltage[59]; (f) monolayer WSe2 SHG intensity as the function of applied gate voltage and SHG emission energy[59].

除了將天然反演對稱的雙層TMDCs 調制出二次諧波信號外, 另一類重要的工作是電調控單層的材料. 單層的TMDCs 受限于較小的光物質相互作用截面, 只能產生有限的二階非線性極化率. 電調控二維材料的二次諧波將對集成的二維非線性器件產生巨大的影響. 華盛頓大學的Seyler 等[59]在2015 年報道了單層WSe2室溫下四倍, 低溫下接近一個量級的二次諧波電調制增強, 并且他們將這種二次諧波極大的可調性解釋為在激子共振附近帶電載流子摻雜的結果. 圖6(d)為其器件結構圖, 機 械 剝 離 在300 nm 二 氧 化 硅/硅 上 的 單 層WSe2上通過電子束曝光與熱蒸發做了釩/金電極,同樣為了避免燒壞器件, 此處通過頂部的金電極與背柵的n 摻雜硅形成垂直電場. 室溫下, Seyler 等首先在WSe2的A 激子(Eg= 1.66 eV)共振能量附近發現, 最大的二次諧波調制出現在激發能量正好與A 激子產生共振的情況下, 并且正向與反向的偏壓會分別抑制與增強WSe2的二次諧波信號. 此時最大的調制范圍約為不加偏壓時的4 倍(圖6(e)), 而激發波長偏離A 激子共振僅30 meV后將不會出現任何調制作用. 這種極大依賴激發波長且與激子共振密切相關的現象使Seyler 等進一步進行了低溫的實驗. 在低溫下他們將激發光的能量從0.85 eV 到0.875 eV 進行了掃描, 在偏壓為–40 V 時1.74 eV 處出現一個二次諧波信號峰, 而當正向增加偏壓信號峰消失直到更高的正向偏壓時1.71 eV 低能量處出現另一個二次諧波信號峰.這種二次諧波調制信號隨激發能量以及偏壓的變化本質上其實是因為垂直電場造成了WSe2中的中性激子X0的摻雜, 使其在高的正向偏壓下吸收負電荷形成帶負電的三激子X–, 而在高的負向偏壓下吸引正電荷形成帶正電的三激子X+[15]. 單層的WSe2被夾在n 摻雜硅與金電極之間像被至于一個平行板電容器之間, 垂直電場雖然不會產生電流但是會額外引入正負電荷, 正負電荷在電場的作用下被拉開吸附于平行板電容器的上下兩側也就造成了材料的摻雜. 又因為不同帶電激子和中性激子的發射波長不同(一般來說中性激子的發射波長更藍), 因此激子共振導致的WSe2二次諧波出射呈現出對于電場以及激發波長特別敏感的特性. 不同激子種類對于二維材料二次諧波強的可調性有著非常重要的意義.

4.2 應變調控二次諧波

應變調控在納米材料的研究中也是廣泛存在的, 它通常能夠改善納米材料的光電性能. 比如現代的硅基場效應晶體管中, 應變被用來減小載流子的有效質量并提高載流子遷移率[68]; 同時應變還能使某些間接帶隙的半導體材料變為直接帶隙,極大地提高了它們的輻射符合效率[69]. 在二維TMDCs 中, 較好的韌性使它們成為了應變場調控天然的備選材料, 二維材料能夠承受最大約10%的應變[70,71], 相比硅的應變閾值約1.5%高了6 倍以上. 扭曲或折疊二維TMDCs 已經取得了很多光電效應上的調制, 比如使層狀二維半導體中激子形成激子凝聚態[72], 或產生單光子出射[72,73]. 在非線性光學的領域中, 應變調制二次諧波的歷史已經有數十年之久, 在塊體中心對稱的硅中, 應變曾被用來打破其中心反演對稱產生二次諧波[74]. 在層狀的二維材料中, 由于二次諧波對于應變非常敏感,因此應變調制二維材料二次諧波是非常有前景的.

2017 年Liang 等[26]報道通過單軸的微弱拉伸應變, 實現了對二硒化鉬二次諧波偏振的調控. 在Liang 等的實驗中, 化學氣相沉積生長的三角形單層二硒化鉬首先通過濕法轉移到了可彎曲的丙烯酸(云母)襯底上, 在施加微弱單軸應變的情況下,二硒化鉬的二次諧波強度發生迅速衰減, 這表明二次諧波對于應變的影響非常敏感. 隨后, Liang 等在單層二硒化鉬的扶手椅以及Z 字形方向分別施加單軸應變, 并通過同時旋轉激發光與檢偏器記錄不同應變大小與二次諧波的偏振情況. 理論上, 在沒有應變作用的情況下, 總的二次諧波強度等于平行與垂直的二次諧波偏振的疊加, 即ISHG=ISHG//+ISHG⊥, 與激發光和樣品的扶手椅方向無關, 是一個定值, 并且它沒有極化方向, 因此極化圖是一個圓(圖7(a)下圖, 橙色). 但是當在二硒化鉬的扶手椅方向上施加單軸應變后, 偏振的二次諧波極化圖出現了扭曲的現象, 平行偏振時施加應變方向的花瓣明顯極化強度減小并隨著應變增加而越發減弱, 總的二次諧波也不再是個定值而在施加應變的方向極化圖內陷(圖7(a)下圖, 紫色). 施加應變后的這種變化可以由二硒化鉬各向異性的打破來解釋. 在扶手椅方向施加單軸應變后, 因為C3對稱軸的消失, 二硒化鉬的晶體對稱性由三倍旋轉對稱的D3h變成了C2v, 且它的二階非線性矩陣也發生了變化, 這使得偏振的二次諧波強度不再遵循公式ISHG//=|d22cos 3θ|2, 而是[26]由

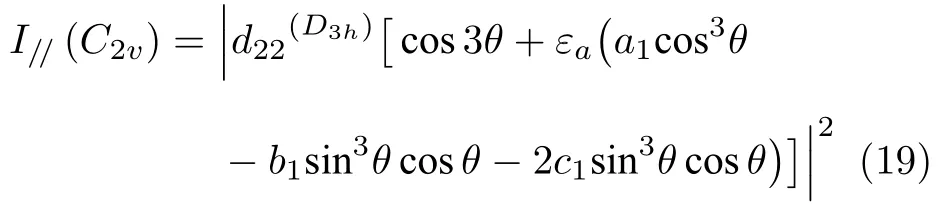
確定, 其中a1,b1,c1是由應變引入的二硒化鉬二階非線性矩陣的變化,ea是指施加在扶手椅方向上的應變. 因此, 基于二次諧波偏振對應變的敏感變化, 使得通過二次諧波監控微弱應變成為可能.

2018 年, Mennel 等[75]在此基礎之上, 借用了Lyubchanskii 等[76]提出的光彈性效應張量理論,將機械剝離二維材料的應變場張量成像精確到了衍射極限. 在Mennel 等的理論中, 應變與二階非線性極化率可以由光彈張量聯系起來[75]:

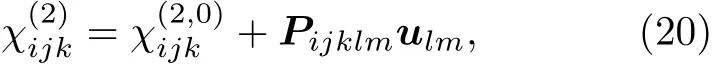
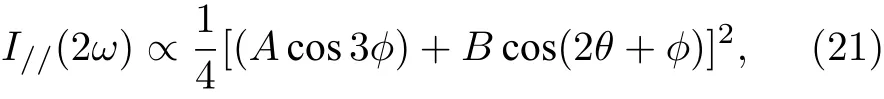
式中,A= (1－n)(p1+p2)(exx+eyy) + 2c0, 而B=(1 +n)(p1－p2)(exx－eyy), 其中p1和p2是光彈參數,exxeyy是基本的應變,q是基本應變取向,f是偏振角(即入射電場方向與二維材料扶手椅方向的夾角),c0是不加任何應變下的二階非線性極化率.根據(20)式, 計算出了光彈張量就能通過二次諧波的測試反過來計算施加在材料上的應變場. 因此, 在通過單層MoS2上施加不同方向的單軸應變場并檢測二次諧波偏振, Mennel 等得到了光彈張量的大小并最終通過計算多個角度的二次諧波偏振成像出單層MoS2的應變場分部, 其分辨率達入射光的衍射極限為280 nm (圖7(b)).

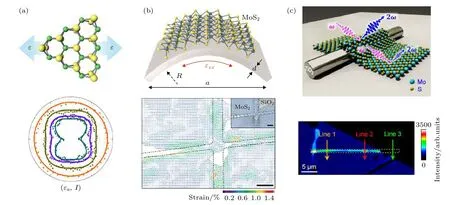
圖7 應變調控二次諧波 (a)軸向拉升應變導致MoSe2 二次諧波偏振變化[26]; (b)通過二次諧波表征MoS2 的全應變場[75]; (c) TiO2/MoS2 異質結結區處應變提高MoS2 二次諧波[77]Fig. 7. Strain modulated SHG: (a) MoSe2 SHG polarization changed by uniaxial tensile strain[26]; (b) uniaxial strain map of MoS2 monolayer flake[75]; (c) schematic illustration (up) and SHG mapping (down) of TiO2/MoS2 structure[77].

2019 年, Li 等[77]報道了將機械剝離的MoS2與二氧化鈦(TiO2)納米線相結合, 在二維/一維的體系中通過不同取向的自發應變實現了對MoS2二次諧波偏振的調控. 在二次諧波強度成像的表征中, MoS2/TiO2異質結的區域比單層MoS2不均勻的增強了十倍, 而純TiO2區域卻不會產生任何信號. 因此這種異質結區域二次諧波信號的增強并不是來源于二氧化鈦的直接貢獻. 通過時域有限差分模擬計算, Li 等確定頂層的MoS2與納米線之間貼合的區域對入射電場產生極大的限域作用, 這是由于TiO2在可見波段是一種高反射系數低損耗的材料, 因此異質結區域的二次諧波強度將被大大提高. 隨后納米線長軸與MoS2扶手椅方向呈不同夾角q的異質結被制備出來, 并且偏振的二次諧波表征發現異質結區域的極化圖不在表現出6 倍的旋轉對稱性圖樣, 而是與夾角q相關, 證明異質結的二次諧波可以被方向性的調制. Li 等通過二維材料應變場來解釋這一現象[77]:

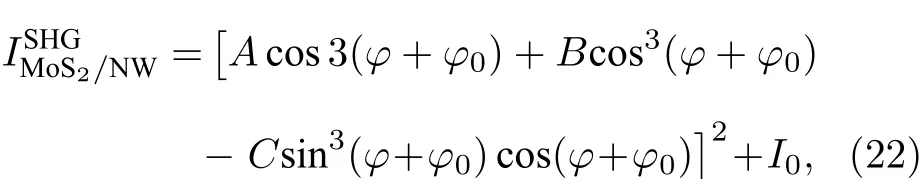
其中,j0是初始MoS2扶手椅方向與入射光方向的夾角;j是測試時樣品旋轉的角度;A,B和C是根據異質結結構決定的三個張量元, 它們都是常數.(22)式中, 第一項代表MoS2晶體結構導致的二次諧波, 而后兩項是由納米線產生的應變場造成的二次諧波, 它將影響整體異質結的二次諧波偏振. 通過對比異質結區域與純的單層MoS2二次諧波偏振, 不同取向的應變場對于MoS2二次諧波的提高也被計算出來.

4.3 其他調制方式

除了上述介紹的在二維材料中常見的調制方式, 近年來諸如周期性陣列結構以及超表面[78]等特殊結構可以調控入射光的相位[79,80]從而控制二維材料二次諧波的出射. 這些新型的調制方式與調制結果開拓了集成非線性光電器件新的領域.

2019 年, Busschaert 等[81]報道通過結合MoS2與周期性含有相位的表面等離激元陣列, 實現了方向可控的二次諧波出射. 在Busschaert 等的實驗中, 周期性的陣列由電子束曝光制作的金納米天線組成, 通過調整金納米棒的長度, 可以控制局域表面等離子體共振與激發光相匹配, 因此提高MoS2/陣列二次諧波的發射效率. 特別地, 通過控制納米天線的長度及距離, 帶有相位的陣列結構得以實現, 它由陣列因子決定[81]:

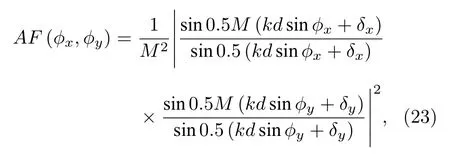
式中,M是每一行(列)的天線數目;d是天線間的距離;k是玻璃襯底上二次諧波出射的波矢,k=2πnglass/lSH, 其中nglass= 1.55;fx和fy是出射角度;dx和dy是納米天線x和y方向上的相位梯度.總的來說, 大面積的納米天線陣列可以產生一個帶有梯度的二次諧波輻射場, 而相位梯度的控制可以通過設計dx以及dy完成. 圖8(b)是Busschaert等在相位dx=dy= 0 時的實驗(散點)和模擬(連線)的結果, 可以看出它們非常符合.

2018 年, 華中科技大學的Chen 等[82]結合表面等離激元超表面和WS2構成了超透鏡, 實現了對二次諧波在出射方向上的聚焦. 超表面上存在不同方向的矩形小孔, 它們的長軸與實驗室坐標x軸的夾角定義為q. 根據理論, 左圓(右圓)偏振的基頻光通過超表面上的矩形小孔時, 帶有右圓(左圓)偏振的基頻光將會被延遲2q個相位同時保持原有的振幅. 當基頻光繼續激發超表面上的WS2后, 因為產生的二次諧波是二階非線性光學過程, 相位延遲將會變成4q. 基于上述超表面調控入射光相位的理論, Chen 等制備了含特殊變化角度q的超表面, 并將其設計成了超透鏡. 同普通的光學透鏡類似, 在滿足了相位j(x,y)條件[82]:

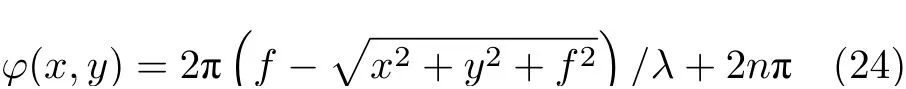
的情況下, 超透鏡能夠實現對入射光的聚焦. 其中l是激發光波長, 實驗中設定為405 nm 對應于產生的二次諧波波長,f是透鏡的焦距, 實驗中設為50 μm. 相位條件2q(x,y) (2q(x,y) =j(x,y)/2)則通過模擬獲得. 最終在實驗上入射光通過超表面激發WS2后, 在傳播方向z上50 μm 處聚焦的的二次諧波被觀測到(圖8(d)). 這種在可見光波段通過超表面調控二維材料非線性的方法在超表面的研究中開創了先例并且為全光學產生漩渦光束提供了可能.

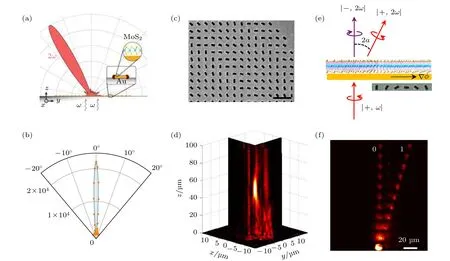
圖8 超表面調控二次諧波 (a)控制納米天線相位梯度導向二次諧波出射方向[81]; (b) 相位d x = d y = 0 時MoS2 二次諧波出射在0°[81]; (c) 周期性的矩形金小孔構成的超表面結構[82]; (d)超表面/WS2 構成的超透鏡對二次諧波在傳播方向上形成聚焦效果[82]; (e)金超表面導向二階谷光子的原理圖[79]; (f)實際的二階光場變化, 0 和1 代表強度等級[79]Fig. 8. Metasurfaces modulated SHG: (a) Schematic illustration of a MoS2-gold phased array antenna steering SHG emission[81]; (b) polar plot of the calculated (line) and measured (points) SH pattern along the intensity maximum when phase delay d x = d y = 0[81];(c) the SEM image of the fabricated gold metasurface with rectangular nanoholes of different orientation[82]; (d) the experimental results of SHG focusing by using the hybrid metasurfaces[82]; (e) schematic representations of steering second-harmonic waves on RCP pumping with monolayer WS2[79]; (f) evolution of the light field for the case shown in (c), “0” and “1” label the intensity order[79].

超表面調控入射光的相位能力結合二維TMDCs 雙光子能谷選擇效應賦予了研究者操縱能谷出射光電子的可能. 2019 年新加坡國立大學的Hu 等[79]報道了通過金屬超表面可以控制和導向WS2的二階非線性谷光子. 圖8(e)是他們實驗的簡化示意圖, 由聚焦離子束刻蝕形成的金超表面上有幾百納米的矩形小孔呈一定規則周期性排列,激發光通過超表面后不但能形成表面等離激元效應限域基頻電場, 同時還能被周期性排列的小孔導向形成Pancharantnam-Berry 相位梯度, 因此可以將非線性谷光子導向自由空間. 理論上, 對于右圓偏振(right circularly polarized, RCP)的入射光(|+,ω〉 )經過金的超表面將會被分成兩部分: 沒有任何幾何相位殘余的右圓偏振光以及帶有幾何相 位ei2q的 左 圓 偏 振(left circularly polarized,LCP)光(|?,ω〉 ). 在二次諧波的過程中, 這兩個分量將會根據第3 節提到的雙光子選擇定則變化: 來自+K谷的二階右圓偏振光子將會擁有兩倍的幾何相位ei4q, 而來自－K谷的二階左圓偏振光子將不會擁有任何幾何相位. 因此通過設計超表面上矩形小孔的周期性及角度, 可以形成動量匹配并導向二階谷光子的相位梯度. 圖8(f)是Hu 等的實驗結果圖, 帶有相位梯度的激發光激發WS2后形成二次諧波并在不同的傳播長度形成不同的傳播方向.其中有兩階能夠清晰的辨認: 第0 階來自－K谷的垂直偏振光(|?,2ω〉 )以及第1 階來自K谷的平行偏振光(|+,2ω〉 ).

5 二次諧波信號增強

原位生長相位匹配的二維材料以及外部施加電場、應變場的調制方法在二次諧波的信號增強方面已經展現出了許多成果, 但二維材料一個或幾個原子層的厚度、與光相互作用截面小依然在一定程度上限制了它的二次諧波轉化效率. 除了通過二維材料結構設計, 也可以利用增強相互作用的局域光場, 得到增強的二次諧波信號. 表面等離激元結構、光子晶體及納米微腔, 能夠限域入射電場產生局域高效的電場增強從而改變二維材料光物質相互作用弱這一劣勢. 同時它們還能結合新型材料或者調制工藝, 最終甚至能達到相比單層好幾個量級增強的二次諧波效應.

5.1 表面等離激元增強二次諧波

表面等離激元效應源于金屬的自由電子在入射光場的作用下產生的集體振蕩行為, 它分為局域表面等離激元和表面等離極化激元兩種[83]. 在近數十年的發展中, 表面等離激元結構已經由納米顆粒[84]逐漸轉變成通過電子束曝光制作的特殊金屬納米周期性結構, 后者將能更好的限域入射光場,并且已經在提高材料量子效率[85?87]、產生法諾共振[88]和激子-表面等離極化基元強耦合[89?91]等研究上產生了非常大的突破.

2020 年, Han 等[92]通過將NPoM (nanoparticle on the mirror)模型構成的表面等離激元納米腔, 實現了超過300 倍的二次諧波增強. 在實驗中,單層的WS2置于銀納米顆粒與銀膜之間, 中間通過三氧化二鋁作為介電層防止電子轉移. 因為銀納米顆粒與銀膜可以形成強的電磁場耦合, 因此可以調控其表面等離激元共振(即調整介電層的厚度)與WS2二次諧波發射波長相匹配. 這種經典的NPoM 納米腔模型利用了局域表面等離激元共振產生的電場限域, 使得波長匹配下的納米腔能極大地提高入射電場強度, 因此提高WS2的二次諧波效率.

除了局域表面等離激元共振, 利用表面等離極化激元也能打破反演對稱性, 實現對目標信號的增強. 2018 年, Wen 等[93]報道通過表面等離激元熱電子的注入使機械剝離2H 相兩層的WSe2產生了二次諧波. 如圖9(b)所示, 由電子束曝光與熱蒸發制作的金納米棒周期性陣列選擇性的修飾在了部分機械剝離的兩層的WSe2上, 構成了表面等離激元/半導體的結構. 同時為了進行對照, 另一組實驗中表面等離激元陣列與兩層WSe2之間插入了四層的氮化硼作為介電層. 隨后, 與表面等離激元共振的800 nm 飛秒激光用來激發混合結構的二次諧波. 如圖9(b)下圖光譜, 兩層的二硒化鎢幾乎測不到二次諧波的信號, 這是由于其存在的反演對稱性所致. 最強的二次諧波信號出現在表面等離激元結構與兩層WSe2直接接觸的結構中, 而插入了四層氮化硼的結構與純的表面等離激元結構信號差不多比直接接觸的結構信號低了一個量級. 造成這種現象的原因在于表面等離激元結構與WSe2直接接觸的情況下, 由于熱電子轉移到半導體中打破了反演對稱性, 從而大大提升了兩層WSe2的二次諧波; 四層的氮化硼阻礙了熱電子的轉移, 進而只能測到和表面等離極化基元金屬結構相同的信號. 因此相對于局域表面等離激元對入射電場的增強, 此時表面等離極化激元產生注入的熱電子是二次諧波增強的主要貢獻. 通過表面等離激元激發熱電子打破反演對稱性能夠實現瞬態的二次諧波增強(轉移時間約為2 ps), 也為將來瞬態的全光學邏輯電路打下基礎.

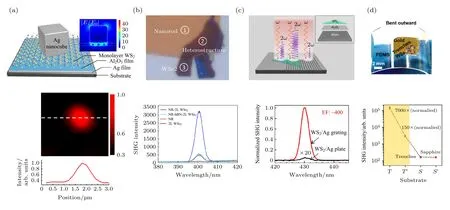
圖9 表面等離激元提高二維材料二次諧波 (a) NPoM 模型中, 納米腔對入射電場產生限域作用(上), 單個納米銀顆粒對WS2 二次諧波成像的增強(下)[92]; (b)對比不同結構的表面等離激元陣列/半導體二次諧波, 其中123 區域分別代表陣列, 兩層WSe2/陣列, 與兩層WSe2 區域[93]; (c) 銀納米柵表面等離激元結構增強WS2 二次諧波達400 倍[94]; (d) PDMS 上表面等離激元陣列對WSe2 二次諧波增強三個量級[95]Fig. 9. SHG enhancement by plasmonics: (a) Nano cavity strongly confines incident light field (up), and SHG enhancement by Ag nanoparticle in monolayer WS2 (down)[92]; (b) compare of SHG signal in different plasmonic array/semiconductor, where points 1, 2,3 represent the area of nanorod, nanorod/bilayer WSe2, and bilayer WSe2, respectively[93]; (c) SHG enhancement factor over 400 in monolayer WS2 reached by Ag nanogroove grating[94]; (d) SHG enhancement over 3 orders in monolayer WSe2 by plasmonic structure on PDMS[95].

隨著表面等離激元工藝的成熟和對局域表面等離激元共振理解的深入, 更加精細能夠更好限域入射電場的結構也被設計出來. 2018 年Shi 等[94]報道通過結合銀納米柵表面等離激元陣列與化學氣相沉積生長的單層WS2, 在C 激子共振下得到了最大約400 倍的二次諧波增強(圖9(c)). 同年Wang 等[95]結合單層的WS2與柔性襯底上表面等離激元結構, 實現了超過3 個量級的二次諧波增強. 柔性襯底上樣品工藝通過模板剝離法[96]制作而來, 其上具有最小達15 nm 溝道的條狀表面等離激元結構. 當入射電場的偏振方向與溝道方向垂直時, 入射電場將被極大的限域在溝道處, 而當入射電場的偏振方向與溝道方向平行時, 則不會出現限域效果. Wang 等對比在溝道處限域電場時與平整的純金襯底上二次諧波的變化, 通過調控條狀結構的大小使局域表面等離激元與800 nm 的激發光共振, 最終獲得了溝道處7000 倍的二次諧波增強(圖9(d)), 并且這種增強效果在向外彎曲柔性襯底達40°、彎曲次數達50 次時依然能保持70%.

5.2 光學微腔、光子晶體增強二次諧波

提高二次諧波轉化效率的另一個方法是耦合光學微腔. 光學諧振腔可以限制激光在腔體中來回振蕩, 從而增強激光與材料的相互作用光程, 極大地提高器件的光轉換效率, 實現器件在低功率下的工作能力[97]. 但是, 一般的光學諧振腔, 如光共振器, 通常被用于實現二維材料器件的線性光學功能, 如熒光增強等[98,99], 其并不適用于二次諧波激發. 原因是這種光學諧振腔只能實現基頻激光共振, 并不能實現二次諧波的同步共振. 基于這個思路, Yi 等[100]設計了雙共振微腔倍頻器件. 這種器件基于一個電壓控制的腔長可調型法布里帕羅微腔. 微腔主要由分布式布拉格反射鏡、MoS2和生長在氮化硅薄膜上的電壓驅動的銀鏡構成(圖10(a)). 當調控法布里帕羅微腔的腔長至共振時, 入射電場與二次諧波發射的電場能同時被增強. 通過電磁場計算, Yi 等設計了特定的氮化硅和氧化物層數的布拉格反射鏡和腔體結構, 以獲得最大的電磁場增強效應. 實驗結果表明, 腔體共振增強后, 器件的二次諧波輸出光強提高了3000 倍.

光子晶體是由不同折射率的介質周期性排列而成的人工微結構, 它能夠調制入射光(電磁波)的傳播行為. 光子晶體的概念最早在1987 年由Yablonovitch[101]在一篇研究自發輻射的論文中提出, 它也可以看成是一種特殊結構的納米微腔. 當電磁波入射到光子晶體表面后, 由于光子晶體的周期性結構與入射波長近似, 所以會使入射光在光子晶體內部反復反射形成類似“能帶”的光學結構, 最終能夠限域特定波長的光而使其他波長的光通過.光子晶體在調制電子-光子相互作用[102]、低閾值激光器[103]、量子信息處理[104]等許多物理和工程領域取得了廣泛的應用. 二維TMDCs 與接觸表面存在很強的范德瓦耳斯相互作用, 因此結合光子晶體有著天然的優勢, 同時由于其超薄的特點, 二維TMDCs 不會干擾光子晶體中波導的傳播或其他功能的實現.

2017 年, Chen 等[105]報道了集成單層的二硒化鉬與硅波導, 實現了二次諧波出射的增強. 實驗的結構原理圖(側視圖)如圖10(b)所示, 在圓形氮化非晶硅/二氧化硅的表面有被刻成光柵狀的結構, 不同大小及周期性的光柵分居表面兩側并分別被用來耦合自由空間的入射電場以及波導產生的倍頻場進入自由空間. 在圓形光柵結構中間的波導區域是機械剝離的單層二硒化鉬, 波導形成的隱失場(evanescent field)將激發二硒化鉬產生二次諧波. 在這個結構中, 為了能夠更好地耦合自由空間的入射電場, 氮化非晶硅的反射系數、入射光的射束輪廓、入射角度、光柵的刻蝕深度及周期性首先通過理論計算得到了優化. 在非線性光學測試中,1550 nm 的飛秒激光用來激發二次諧波, 它的雙光子能量與二硒化鉬的激子產生共振, 這將極大地提高二次諧波過程的效率. 當激發光聚焦在光柵區域時, 對比直接聚焦在單層二硒化鉬, 產生了約5 倍的二次諧波增強. 硅波導增強二次諧波的原理是因為相比于單層的二維材料與激發光有限的作用面積, 這種特殊結構使得整個二硒化鉬都與硅波導相互作用, 極大地拓寬了產生二次諧波的范圍, 同時它也為將來二維半導體材料與硅基結構相結合打下了基礎.

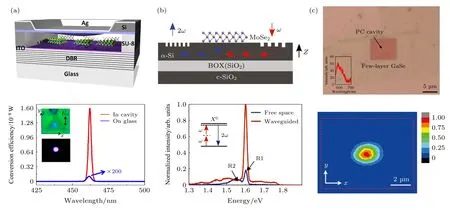
圖10 微腔、光子晶體增強二維材料二次諧波 (a)雙共振法帕納米微腔增強二次諧波[100]; (b)硅波導增強二硒化鉬二次諧波[105];(c)連續激光激發硒化鎵/硅光子晶體結構二次諧波[106]Fig. 10. SHG enhancement by micro cavity and photonic crystal: (a) Enhancement of SHG from monolayer MoS2 in a doubly resonant on-chip optical cavity[100]; (b) enhancement of SHG by silicon waveguide[105]; (c) CW excitation of SHG from GaSe/photonic crystal[106].

2018 年, Gan 等[106]報道通過低能量的連續激光激發了二維硒化鎵/硅光子晶體結構的二次諧波. 由于納米材料非線性系數較小, 非線性過程效率低, 因此通常需要脈沖激光的峰值能量才能激發產生有效的二次諧波. 二維硒化鎵自身有著超過單層MoS2一到兩個量級的二階非線性系數[107], 這使得它成為非常優秀的非線性材料, 同時確保與納米腔隱失場有效的相互作用. 在硒化鎵/硅光子晶體結構中, 光子晶體納米腔被設計成非對稱小孔的基礎上又人為引入了適量缺陷, 這將極大地耦合入射光進入納米腔并且在垂直方向上提高輻射效率[108]. 這樣設計的納米腔品質因數Q接近2000,共振激發時二階非線性過程的增強正比于Q2, 因此即使當0.1 mW 的低能量連續激光垂直入射光子晶體時, 納米腔模共振的隱失場也能有效地激發硒化鎵的二次諧波. 圖10(c)下圖是硒化鎵/硅光子晶體產生二次諧波的成像, 其中有信號的區域在2.5 μm × 2 μm 引入缺陷至非對稱小孔的腔體區域, 也證明了光子晶體納米腔耦合對二次諧波的貢獻. 低能量連續激光激發二次諧波的實現極大地拓寬了二維材料非線性光學的應用領域, 為連續激光頻率轉換器, 上轉換探測器的應用提供了可能.

6 總結與展望

非線性光學是光學領域中一個非常重要的研究方向, 非線性光學的發展對于現代社會的技術進步有著至關重要的作用. 以二維TMDCs 為代表的二維半導體材料的興起帶來了對二維層狀材料非線性光學特別是二次諧波的研究熱潮. 本文從材料到應用的角度總結了二維材料二次諧波的一些相關工作, 首先從材料自身的特點介紹了與二次諧波相關的特性, 然后通過電、應變場以及最新的超表面等手段介紹了不同的調制工作, 最后對如何實現二次諧波信號的提高進行了總結.

最近二維TMDCs 二次諧波的研究也朝著一些新的方向發展. 比如, Jang 等[109]報道, 結合泵浦探測, 他們實現了對機械剝離MoS2瞬態的二次諧波成像, 并且觀察到了強的激子-聲子耦合現象.激子的能量會通過非輻射復合傳遞給聲子, 這種激子-聲子耦合的現象將通過晶格振蕩表現在二次諧波的壽命上: MoS2二次諧波此時存在兩個壽命組分, 其中最初的一兩個皮秒對應于直接帶隙轉移的激子動力學過程, 而之后受晶格的影響則會表現出振蕩的行為[109]. Lin 等[110]報道, 在A 激子附近共振激發WSe2時, 他們發現二次諧波光譜的劈裂,并解釋為量子干涉效應. 量子干涉效應是波粒二象性的標志, 當電子轉移存在不同路徑并且相互作用時, 量子干涉在光譜上常表現為類似法諾共振的非對稱曲線. 這些新的研究方向讓我們看到了二維材料不同于傳統半導體新的特性, 也為發展基于二維材料二次諧波新的應用(如探測系統, 光參量放大系統)提供了可能. 在龐大的二維半導體家族, 找出擁有良好的穩定性、可大面積制備層數可控且擁有非常大的二階非線性系數的最適合用于非線性光學的材料, 基于此實現面向實際應用的高性能非線性光電器件及集成器件, 可能是今后發展的重要方向.