一個新四翼高維超混沌系統的復雜動力學行為研究與仿真

師東生 石煒

摘? 要： 文中構建了一個新的五維超混沌系統，該系統在[x?z]方向和[x?w]方向上均具有四翼特征。通過在Lyapunov指數、龐加萊截面圖、分岔圖以及頻譜圖等方面的仿真與分析，確定具有四翼吸引子的超混沌系統具有更高的Lyapunov指數。迭代生成的序列值分布更為均勻、離散，表明新構建的超混沌系統具有更為復雜的動力學行為，擁有更寬的頻譜帶寬，在通信、信息安全等領域具有更為廣闊的應用前景。

關鍵詞： 高維超混沌系統; 動力學行為; 四翼吸引子; Lyapunov指數分析; 龐加萊截面分析; 功率譜分析

中圖分類號： TN911.7?34? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼： A? ? ? ? ? ? ? ? ? ? ? ? ? 文章編號： 1004?373X（2020）19?0010?04

Abstracts： A new five?dimensional hyperchaotic system is constructed in this paper. The system has four?wing characteristics in both [x?z] and [x?w] directions. By simulation and analysis of Lyapunov exponent， Poincare section， bifurcation diagram and frequency spectrum， it is determined that the hyperchaotic chaotic system with four?wing attractor has higher Lyapunov exponents， and the sequence values generated by iteration are more uniform and discrete. The analysis results show that the newly?constructed hyperchaotic system has more complex dynamic behavior and broader spectrum bandwidth， and has a wider application prospect in communication， information security and other fields.

Keywords： high?dimensional hyperchaotic system; dynamic behavior; four?wing attractor; Lyapunov exponent analysis; Poincare section analysis; power spectrum analysis

0? 引? 言

自1963年美國氣象學家Lorenz發現了第一個三維混沌系統——Lorenz系統以來，諸多學者致力于混沌系統的研究，并相繼推出了許多著名的混沌系統，如：Chen系統、Sprott系統、Lü系統等。由于混沌系統具有遍歷性、有界性、初值敏感性等特點[1]，因而被廣泛地應用于信號處理、信息安全、生物技術等領域。近幾年來，學者們研究發現：低維（三維及以下）的混沌系統由于大都具有少而偏低的Lyapunov指數，從而容易導致混沌系統的動力學行為過于簡單，在信息安全領域會導致密鑰空間偏小、周期窗穩定等缺陷[2?5];高維混沌系統（五維及以上）由于正的Lyapunov指數多于2個，因而復雜性更高、魯棒性更強，在信息安全領域具有更高的可靠性。而具有四翼蝴蝶混沌吸引子的混沌系統具有更為復雜的動力學行為，在信息安全方面具有更高的安全性，于是更多的四翼混沌系統應運而生并得到廣泛應用，如：三維四翼混沌系統[6?8]、四翼超混沌系統[9?13]、分數階四翼混沌系統等[14?15]。

本文構建了一個新的五維超混沌系統，該系統在[x?z]以及[x?w]方向上均具有四翼特征，通過對Lyapunov指數、分岔圖、龐加萊截面和功率譜等方面的仿真研究，確定該超混沌系統具有較高的Lyapunov指數和更為復雜的動力學行為。

1? 新五維超混沌系統

新五維超混沌系統如式（1）所示：

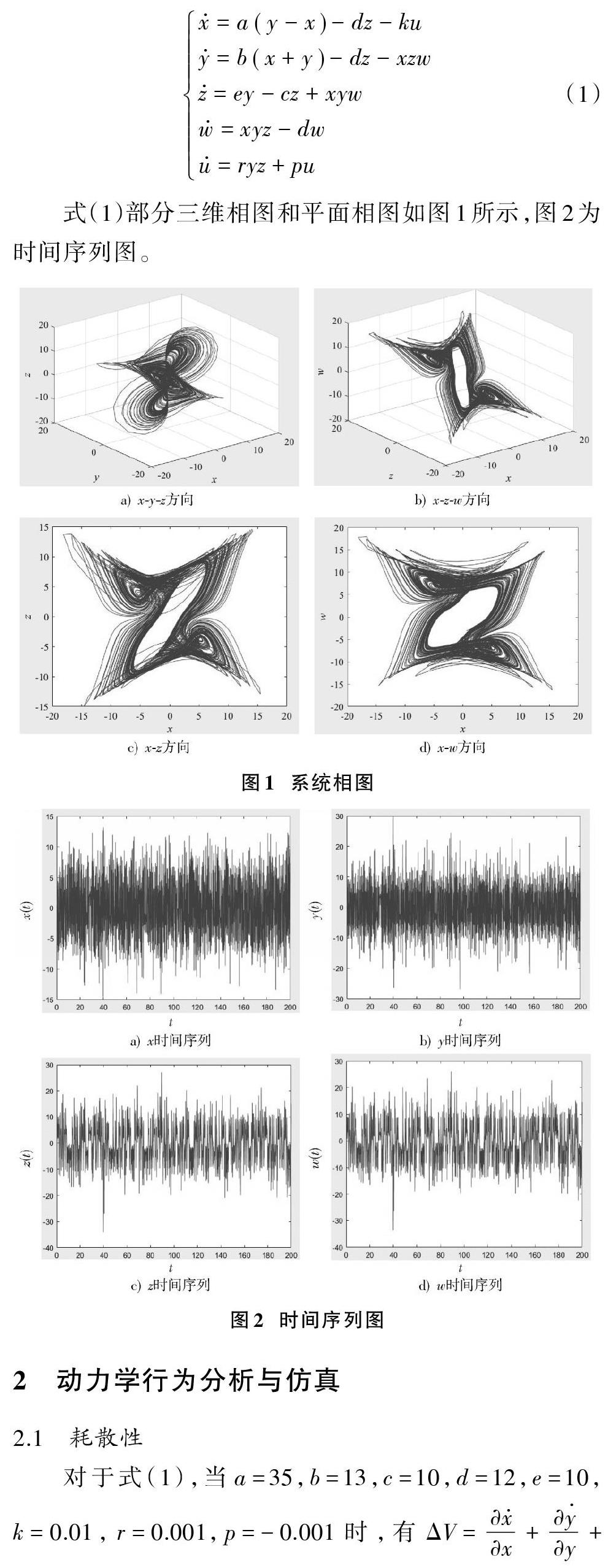
式（1）部分三維相圖和平面相圖如圖1所示，圖2為時間序列圖。

2? 動力學行為分析與仿真

2.1? 耗散性

2.2? 平衡點分析

2.3? Lyapunov指數與分岔圖

Lyapunov指數刻畫了在相空間里系統兩條相鄰的軌道之間收斂和發散的平均指數率[16]。正的Lyapunov指數是引起混沌吸引子局部不穩定的根源，它導致兩個初始值所產生的兩條軌道隨時間以指數方式分離，由于系統是耗散的，所以混沌系統會變得局部不穩定而整體穩定[17]。

從圖4～圖6中可見，當參數[a∈][20，60），具有2個正的Lyapunov指數，系統為超混沌狀態;當[a∈][60，85）時，有1個正的Lyapunov指數，系統為混沌狀態;當[a∈][85，100]時，最大的Lyapunov指數為0，系統為周期運動狀態。當[c∈][6，20]時，具有2個正的Lyapunov指數，為超混沌狀態。當[d∈][2，26]時，具有2個正的Lyapunov指數，為超混沌狀態;當[d∈][27，30]時，只有1個正的Lyapunov指數，為混沌狀態。

分岔圖用來表示當某一參數變化時，系統隨之發生變化的圖示。從圖4～圖6可見，當具有正的Lyapunov指數時，分岔圖也隨之呈密集分布狀態，與式（1）的混沌或超混沌狀態相吻合。

2.4? 龐加萊截面分析

當龐加萊截面上出現[k]個離散的點時，說明系統是[k]周期運動的;當截面出現一條封閉曲線時，說明系統是擬周期運動的;當截面出現成片、并具有分形特征的大量截點時，說明系統處于混沌狀態。

圖7為[x?z]方向和[x?w]方向的龐加萊截面圖，截面圖上均出現了由大量截點構成的具有分形結構的葉片，這些葉片穿越上下吸引界限，從而形成四翼混沌吸引子。

2.5? 頻譜分析

功率譜是將Fourier變化應用到相空間的坐標中得到的系統二維圖形表述。若系統為混沌運動，則呈現連續的譜線，同時可看到噪聲背景和寬峰，并會觀測到尖峰[16]。

圖8為關于[x]，[y]分量的功率譜圖，可見式（1）的頻譜帶寬明顯寬于三維Chen系統和三維Lorenz系統的頻譜帶寬，此特性非常有利于在信息加密等領域的應用。

3? 結? 語

通過對新構建的五維超混沌系統進行仿真測試，發現該系統在[x?z]方向和[x?w]方向上均具有四翼特征，而且具有較高的Lyapunov指數，說明該系統具有更為復雜的動力學行為;其時間序列圖也表明了該系統迭代生成的值分布均勻而密集，離散性強;功率譜圖也展示了其具有更為寬厚的頻譜帶寬，說明該系統在信號處理、信息安全等方面具有更為良好的應用前景。

參考文獻

[1] 趙慧，賴強.新三維混沌系統的復雜動力學分析[J].華中師范大學學報（自然科學版），2017，51（2）：155?161.

[2] 朱淑芹，李俊青.一種混沌圖像加密算法的選擇明文攻擊和改進[J].計算機工程與應用，2017，53（24）：113?121.

[3] 朱淑芹，李俊青，王文宏.對改進的基于DNA編碼和混沌的圖像加密算法的安全性分析[J].計算機應用研究，2017，34（10）：3090?3093.

[4] 朱淑芹，王文宏，李俊青.對像素置亂和比特替換混沌圖像算法的破解[J].計算機應用，2017，37（z2）：44?47.

[5] 朱淑芹，王文宏，孫忠貴.對一種混沌圖像加密算法的安全分析和改進[J].計算機工程與應用，2019，55（1）：115?122.

[6] 鮑慧玲，薛華.一個三維四翼混沌系統的分岔分析及其電路實現[J].合肥工業大學（自然科學版），2014，37（1）：155?158.

[7] 齊芳，張曉丹，聶少敏，等.一類3D四翼倍增混沌系統及Hash函數算法[J].濟南大學學報（自然科學版），2016，30（3）：195?202.

[8] WANG Zhen， VOLOS C， KINGNI S T， et al. Four?wing attractors in a novel chaotic system with hyperbolic sine nonlinearity [J]. Optik， 2017， 131： 1071?1078.

[9] DARAS S， MOMENI H R， QI Guoyuan， et al. Four?wing hyperchaotic attractor generated from a new 4D system with one equilibrium and its fractional?order form [J]. Nonlinear dyna?mics， 2012， 67： 1167?1173.

[10] 屈雙惠，容旭巍，吳淑花，等.一個四翼超混沌系統的電路實現及其同步控制[J].華中師范大學學報（自然科學版），2013，47（2）：189?194.

[11] 杜文舉，俞建寧，張建剛，等.一個新四維混沌系統的分岔分析[J].東北師大學報（自然科學版），2014，46（1）：80?87.

[12] 彭再平，王春華，林愿，等.一種新型的四維多翼超混沌吸引子及其在圖像加密中的研究[J].物理學報，2014（24）：97?106.

[13] YU Fei， GAO Lei， GU Ke， et al. A fully qualified four?wing four?dimensional autonomous chaotic system and its synchronization [J]. Optik， 2017， 131： 79?88.

[14] 屈雙惠，張彩霞，楊志宏，等.分數階四翼超混沌系統和分數階Chen系統的異結構同步[J].四川大學學報（自然科學版），2014，51（1）：131?136.

[15] 楊志宏，屈雙惠，吳淑花，等.一分數階四翼超混沌系統的同步控制[J].合肥工業大學學報（自然科學版），2015（6）：857?860.

[16] 陳春濤.一類Lorenz?5D超混沌系統的復雜動力學行為研究[D].廣州：華南理工大學，2015.

[17] 戰凱，姜文剛.一個新四翼超混沌系統及其在圖像加密中應用[J].計算機工程與應用，2017，53（12）：36?44.