群體動(dòng)畫(huà)行為自動(dòng)控制的微粒群優(yōu)化算法

楊亮 張穎 姚奕洋

摘? 要： 為提升群體動(dòng)畫(huà)行為的自主性以及智能性，研究群體動(dòng)畫(huà)行為自動(dòng)控制的微粒群優(yōu)化算法。用戶(hù)輸入群體動(dòng)畫(huà)行為構(gòu)建目標(biāo)后，依據(jù)固定行為規(guī)則規(guī)劃個(gè)體路徑，采用微粒群優(yōu)化算法依據(jù)自上而下的控制過(guò)程為群體動(dòng)畫(huà)內(nèi)個(gè)體選擇最優(yōu)動(dòng)作。其中，微粒群算法步驟如下：初始化微粒群算法參數(shù)、評(píng)價(jià)微粒初始適應(yīng)值、更新微粒群內(nèi)個(gè)體速度和位置、評(píng)價(jià)微粒適應(yīng)值、判定歷史最優(yōu)位置以及適應(yīng)值，適應(yīng)值誤差符合設(shè)定限制時(shí)輸出全局最優(yōu)搜索結(jié)果，并選取Eberhart方法依據(jù)外部環(huán)境變化優(yōu)化微粒群算法，利用最優(yōu)動(dòng)作實(shí)現(xiàn)行為自動(dòng)控制后通過(guò)3ds max軟件渲染功能將最終結(jié)果輸出。通過(guò)實(shí)例分析驗(yàn)證該算法可有效實(shí)現(xiàn)群體動(dòng)畫(huà)行為的自動(dòng)控制，且收斂速度快，具有較高的自主性。

關(guān)鍵詞： 群體動(dòng)畫(huà)行為; 自動(dòng)控制; 微粒群算法優(yōu)化; 動(dòng)作選擇; 行為控制; 實(shí)例分析

中圖分類(lèi)號(hào)： TN911.1?34; TP181? ? ? ? ? ? ? ? ? 文獻(xiàn)標(biāo)識(shí)碼： A? ? ? ? ? ? ? ? ? ? ?文章編號(hào)： 1004?373X（2020）19?0106?05

Abstract： In order to improve the autonomy and intelligence of the group animation behavior， the particle swarm optimization algorithm for the automatic control of group animation behavior is studied. After a user inputs the group animation behavior to construct the goal， the individual path is planned according to the fixed routine behavior rules， and the particle swarm optimization algorithm is used to select the optimal action for the individual in the group animation according to the top?down control process. The steps of particle swarm algorithm are as follows： initialize the parameters of particle swarm algorithm， evaluate the initial particle adaptive value， update the speed and position of individuals in the particle swarm， evaluate the particle adaptation value， determine the historical optimal position and adaptive value， output the global optimal search results when the adaptive value error meets the set limit， select the Eberhart method to optimize the particle swarm algorithm according to changes of external environment， use the optimal action to achieve automatic control of behavior， and output the final result by the rendering function of 3ds max software. It is verified by example analysis that the algorithm can effectively realize automatic control of group animation behavior， and has fast convergence speed and high autonomy.

Keywords： group animation behavior; automatic control; particle swarm algorithm optimization; action selection; behavior control; example analysis

0? 引? 言

以往群體動(dòng)畫(huà)通常采用手繪方式控制個(gè)體行為，采用手繪方式令群體依據(jù)個(gè)體路徑軌跡移動(dòng)具有較高的復(fù)雜性以及繁瑣性[1]。群體動(dòng)畫(huà)是目前計(jì)算機(jī)動(dòng)畫(huà)領(lǐng)域的重點(diǎn)研究方向，群體動(dòng)畫(huà)依據(jù)動(dòng)物成群結(jié)隊(duì)的移動(dòng)形式令大量個(gè)體通過(guò)相同行為聚集于一體，利用有效算法可令群體產(chǎn)生存在某種目的而行進(jìn)的錯(cuò)覺(jué)。群體動(dòng)畫(huà)的誕生推進(jìn)了計(jì)算機(jī)動(dòng)畫(huà)的發(fā)展速度[2]，群體動(dòng)畫(huà)需要群體具有整體運(yùn)動(dòng)協(xié)調(diào)一致性，但群體內(nèi)個(gè)體具有獨(dú)特性，因此群體動(dòng)畫(huà)自動(dòng)控制具有一定難度。

微粒群算法是一種有效的群體演化算法，該算法將控制目標(biāo)比作鳥(niǎo)群或魚(yú)群，依據(jù)鳥(niǎo)群或魚(yú)群捕食過(guò)程的社會(huì)行為令動(dòng)畫(huà)內(nèi)個(gè)體依據(jù)群體行為行動(dòng)[3]。微粒群算法兼具反饋與信息共享機(jī)制，具有魯棒性好、簡(jiǎn)單易行的優(yōu)勢(shì)。微粒群算法已廣泛應(yīng)用于靜態(tài)優(yōu)化問(wèn)題中，并取得良好成效，將微粒群算法應(yīng)用于動(dòng)態(tài)問(wèn)題中，往往容易陷入局部最優(yōu)導(dǎo)致較難獲取動(dòng)態(tài)目標(biāo)最優(yōu)解[4]。傳統(tǒng)的微粒群算法內(nèi)全部粒子選取最優(yōu)個(gè)體作為全局極值，容易陷入局部最優(yōu)。針對(duì)以上缺陷對(duì)微粒群算法優(yōu)化，改進(jìn)微粒群算法中粒子的運(yùn)動(dòng)方式[5]，獲取最優(yōu)的自動(dòng)控制效果。微粒群算法具有群體智能性，將微粒群算法應(yīng)用于群體動(dòng)畫(huà)行為自動(dòng)控制中，需要實(shí)時(shí)檢測(cè)粒子周?chē)h(huán)境變化，并以最短時(shí)間尋取最優(yōu)解[6]。研究群體動(dòng)畫(huà)行為自動(dòng)控制的微粒群優(yōu)化算法，可令群體內(nèi)動(dòng)畫(huà)角色具有自主性，實(shí)現(xiàn)行為控制簡(jiǎn)單化以及角色運(yùn)動(dòng)自然逼真化，并具有良好的全局尋優(yōu)性能，可快速實(shí)現(xiàn)群體動(dòng)畫(huà)自動(dòng)控制。

1? 微粒群優(yōu)化算法構(gòu)建

1.1? 群體動(dòng)畫(huà)

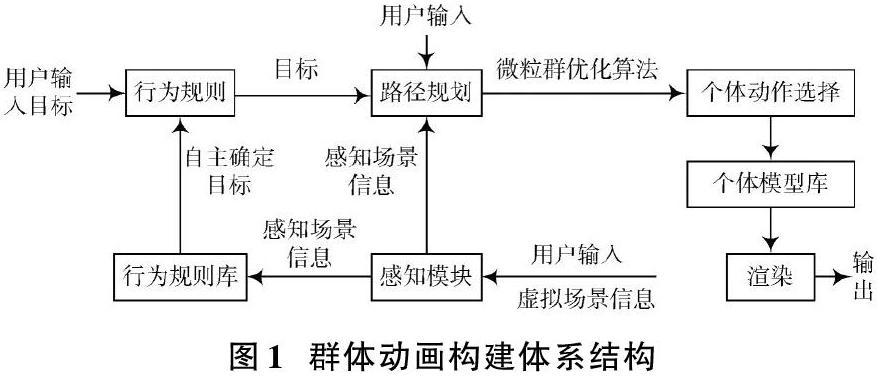
群體動(dòng)畫(huà)是依據(jù)人類(lèi)以及動(dòng)物群體行為構(gòu)建三維群體動(dòng)畫(huà)的方式[7]，群體動(dòng)畫(huà)已廣泛應(yīng)用于影視作品、公共安全以及各類(lèi)大型游戲中。群體以及個(gè)體在群體動(dòng)畫(huà)中的運(yùn)動(dòng)行為控制是群體動(dòng)畫(huà)研究的重要方向，群體動(dòng)畫(huà)構(gòu)建體系結(jié)構(gòu)圖如圖1所示。

群體動(dòng)畫(huà)需要遵循固定原則，群體動(dòng)畫(huà)模擬過(guò)程中賦予群體內(nèi)個(gè)體最基本的行動(dòng)能力。群體動(dòng)畫(huà)內(nèi)全部個(gè)體可依據(jù)其余個(gè)體的運(yùn)動(dòng)情況決定運(yùn)動(dòng)路徑。從圖1可以看出，用戶(hù)輸入群體動(dòng)畫(huà)構(gòu)建目標(biāo)后，依據(jù)固定行為規(guī)則規(guī)劃個(gè)體路徑[8]，確定群體動(dòng)畫(huà)內(nèi)個(gè)體行動(dòng)路徑后，采用微粒群優(yōu)化算法依據(jù)自上而下的控制過(guò)程為群體動(dòng)畫(huà)內(nèi)個(gè)體選擇最優(yōu)動(dòng)作，個(gè)體動(dòng)作完成后通過(guò)3ds max軟件的渲染功能將最終結(jié)果輸出。

采用3ds max軟件建立群體動(dòng)畫(huà)模型，建立過(guò)程需要依據(jù)如下原則：

1） 群體動(dòng)畫(huà)內(nèi)全部個(gè)體需要有自身個(gè)體空間，為避免個(gè)體空間受到侵占，個(gè)體在其他個(gè)體進(jìn)入安全空間時(shí)需要遠(yuǎn)離;

2） 群體動(dòng)畫(huà)內(nèi)全部個(gè)體需要與其他個(gè)體運(yùn)動(dòng)方向保持一致，群體動(dòng)畫(huà)內(nèi)全部個(gè)體運(yùn)動(dòng)方向大致相同;

3） 群體動(dòng)畫(huà)內(nèi)小群體在周?chē)鸁o(wú)障礙物時(shí)可與周?chē)后w融為一體，群體動(dòng)畫(huà)設(shè)計(jì)過(guò)程中應(yīng)盡量避免碰撞產(chǎn)生。

群體動(dòng)畫(huà)行為自動(dòng)控制策略主要分為自下而上控制以及自下而上控制兩部分。

群體動(dòng)畫(huà)中的個(gè)體依據(jù)自身判斷決定行為的過(guò)程稱(chēng)之為自下而上的控制過(guò)程[9]。自下而上的自動(dòng)控制方法可依據(jù)周?chē)h(huán)境感知令個(gè)體與周?chē)h(huán)境以及周?chē)鷤€(gè)體實(shí)現(xiàn)自主交互，通過(guò)自主交互展示群體特征。

用戶(hù)意識(shí)決定群體動(dòng)畫(huà)中個(gè)體行為的控制過(guò)程稱(chēng)之為自上而下的控制過(guò)程，用戶(hù)通過(guò)控制群體動(dòng)畫(huà)中個(gè)體令全部個(gè)體依據(jù)用戶(hù)意識(shí)實(shí)現(xiàn)自主控制。

選取微粒群優(yōu)化算法采用自上而下的控制過(guò)程實(shí)現(xiàn)群體動(dòng)畫(huà)行為自動(dòng)控制。用戶(hù)輸入群體動(dòng)畫(huà)行為的控制參數(shù)后，利用控制參數(shù)指定群體動(dòng)畫(huà)內(nèi)個(gè)體初始狀態(tài)，群體動(dòng)畫(huà)內(nèi)個(gè)體依據(jù)用戶(hù)控制參數(shù)實(shí)現(xiàn)自主控制。

1.2? 微粒群算法

微粒群算法將所需尋優(yōu)的全部個(gè)體視作無(wú)質(zhì)量、無(wú)體積的微粒存儲(chǔ)于[B]維搜索空間內(nèi)，設(shè)全部粒子飛行速度固定，依據(jù)全部粒子以及個(gè)體粒子的飛行經(jīng)驗(yàn)動(dòng)態(tài)調(diào)整各粒子的飛行速度[10]，通過(guò)個(gè)體對(duì)環(huán)境的適應(yīng)度，令群體內(nèi)全部個(gè)體向完成設(shè)定區(qū)域移動(dòng)。

設(shè)微粒群存在于[B]維搜索空間中，其中含有微粒數(shù)量為[m]，第[i]個(gè)微粒于該搜索空間的位置用[Yi=yi1，yi2，…，yiB]表示，且[i=1，2，…，m]，該位置即為優(yōu)化問(wèn)題的潛在解，利用該位置可獲取微粒適應(yīng)值，空間位置的優(yōu)劣情況可依據(jù)所獲取適應(yīng)值評(píng)估。用[Qi=qi1，qi2，…，qiB]表示第[i]個(gè)微粒移動(dòng)過(guò)程中最優(yōu)位置，即個(gè)體歷史最優(yōu)位置[11]，則該位置對(duì)應(yīng)適應(yīng)值即為該微粒個(gè)體歷史最優(yōu)適應(yīng)值，用[Hi]表示，全部微粒移動(dòng)過(guò)程中經(jīng)歷的位置中最優(yōu)位置即為該微粒群全局歷史最優(yōu)位置，用[Qg=qg1，qg2，…，qgB]表示，該位置對(duì)應(yīng)的適應(yīng)值即為全局歷史最優(yōu)適應(yīng)值，用[Hg]表示。

微粒群內(nèi)微粒個(gè)體的移動(dòng)速度用[Ui=ui1，ui2，…，uiB]表示，微粒[i]于[b]維[1≤b≤B]空間的運(yùn)動(dòng)在每次迭代過(guò)程中均需依據(jù)以下公式移動(dòng)：

式中：[w]與[e1]，[e2]分別表示慣性權(quán)值以及加速系數(shù);[r1]，[r2]表示[0，1]范圍內(nèi)變化的隨機(jī)數(shù)。式（2）為微粒求解空間內(nèi)，微粒互相影響造成的運(yùn)動(dòng)位置調(diào)整。

微粒群算法步驟如下：

1） 初始化微粒群算法的規(guī)模、慣性權(quán)值、最大允許迭代次數(shù)、適應(yīng)值誤差限制、加速系數(shù)、微粒初始速度、初始位置、位置限制和飛行速度限制等參數(shù);

2） 評(píng)價(jià)微粒初始適應(yīng)值，設(shè)置微粒群內(nèi)的個(gè)體歷史最優(yōu)值以及全局歷史最優(yōu)值[12];

3） 更新微粒群內(nèi)個(gè)體速度和位置，并通過(guò)限幅處理微粒群更新后速度以及位置;

4） 評(píng)價(jià)微粒適應(yīng)值;

5） 比較各微粒的個(gè)體歷史最優(yōu)適應(yīng)值以及當(dāng)前適應(yīng)值，將最優(yōu)的適應(yīng)值保存設(shè)置為歷史最優(yōu)適應(yīng)值，將該位置更新為個(gè)體歷史最優(yōu)位置;

6） 將微粒群內(nèi)全部個(gè)體的全局最優(yōu)適應(yīng)值與此時(shí)適應(yīng)值對(duì)比[13]，保留最優(yōu)的適應(yīng)值作為全部歷史最優(yōu)適應(yīng)值，此時(shí)位置為全局歷史最優(yōu)位置;

7） 當(dāng)適應(yīng)值誤差符合設(shè)定的適應(yīng)值誤差限制時(shí)，符合停止條件，算法結(jié)束，輸出全局最優(yōu)搜索結(jié)果;否則，返回至步驟3）。

1.3? 微粒群優(yōu)化算法

為令微粒群算法不易受到外部環(huán)境影響，令環(huán)境變化時(shí)該算法仍具有較強(qiáng)的適應(yīng)性，可準(zhǔn)確感應(yīng)環(huán)境變換，并在環(huán)境出現(xiàn)變化時(shí)可準(zhǔn)確跟蹤最優(yōu)解，基于微粒群算法改進(jìn)全局極值表示方法，優(yōu)化的微粒群算法將全局極值采用所獲取的局部最優(yōu)平均值替代[14]，計(jì)算每個(gè)微粒在微粒群進(jìn)化一代時(shí)當(dāng)前局部最優(yōu)適應(yīng)度值，并獲取微粒群內(nèi)個(gè)體局部最差適應(yīng)度值以及局部最優(yōu)適應(yīng)度值，計(jì)算局部最差適應(yīng)度值與局部最優(yōu)適應(yīng)度值的和與差，獲取和與差的比值，利用該比值獲取微粒群內(nèi)全部個(gè)體最優(yōu)適應(yīng)度值平均值，微粒群全局最優(yōu)適應(yīng)度值選取平均值與比值相差獲取的積，其計(jì)算公式如下：

將式（3）獲取的[Qm]代替微粒群優(yōu)化算法的[Qg]更新微粒速度。

微粒群需要具備快速感應(yīng)外部環(huán)境變化的能力，才可令其快速跟蹤動(dòng)態(tài)機(jī)制，微粒群算法感受環(huán)境變化后需要及時(shí)采用響應(yīng)機(jī)制。選取Eberhart方法應(yīng)用于微粒群優(yōu)化算法中，感應(yīng)微粒群算法隨外部環(huán)境變化情況。當(dāng)微粒群全局極值存在變化時(shí)，表明該微粒群環(huán)境出現(xiàn)變化導(dǎo)致微粒群全局極值發(fā)生變化[15]。微粒群環(huán)境存在變化時(shí)，需要及時(shí)獲取微粒群算法內(nèi)全部微粒的全局極值以及局部極值，并將局部極值與全局極值比較后依據(jù)存在的最優(yōu)適應(yīng)度值微粒距離排序，將與全局極值距離較小的6%微粒重新初始化，擴(kuò)大搜索范圍繼續(xù)搜索，令微粒群具有較高多樣性，繼續(xù)進(jìn)化尋找環(huán)境變化后全局最優(yōu)值。

2? 實(shí)例分析

在上述研究的基礎(chǔ)上，對(duì)本文所研究群體動(dòng)畫(huà)行為自動(dòng)控制的微粒群優(yōu)化算法進(jìn)行模擬實(shí)驗(yàn)，采用Microsoft Visual Studio .NET平臺(tái)為Autodesk Maya 2016軟件開(kāi)發(fā)的群體動(dòng)畫(huà)編程本文算法。

Autodesk Maya 2016軟件開(kāi)發(fā)的群體動(dòng)畫(huà)原始圖如圖2所示。

采用本文算法自動(dòng)控制群體動(dòng)畫(huà)內(nèi)個(gè)體移動(dòng)至圈內(nèi)行為結(jié)果如圖3所示。

采用本文算法自動(dòng)控制群體動(dòng)畫(huà)內(nèi)個(gè)體移動(dòng)至看臺(tái)行為結(jié)果如圖4所示。

通過(guò)圖3，圖4實(shí)驗(yàn)結(jié)果可以看出，采用本文算法可實(shí)現(xiàn)群體動(dòng)畫(huà)內(nèi)個(gè)體行為自動(dòng)控制，且群體動(dòng)畫(huà)真實(shí)感強(qiáng)，驗(yàn)證了本文算法自主控制的有效性，說(shuō)明本文算法可行，采用本文算法控制動(dòng)畫(huà)群體具有人工智能性，可有效再現(xiàn)群體覓食行為。

采用本文算法自動(dòng)控制群體動(dòng)畫(huà)內(nèi)個(gè)體移動(dòng)至圈內(nèi)行為的進(jìn)化過(guò)程如圖5所示，為直觀展示本文算法的控制性能，將本文算法與Q?學(xué)習(xí)算法以及目標(biāo)跟蹤算法對(duì)比。

采用本文算法控制群體動(dòng)畫(huà)內(nèi)個(gè)體移動(dòng)至看臺(tái)行為進(jìn)化過(guò)程如圖6所示，將Q?學(xué)習(xí)算法以及目標(biāo)跟蹤算法作為對(duì)比算法。

通過(guò)圖5，圖6自動(dòng)控制群體動(dòng)畫(huà)內(nèi)個(gè)體移動(dòng)至圈內(nèi)以及移動(dòng)至看臺(tái)行為進(jìn)化過(guò)程可以看出：最優(yōu)解動(dòng)態(tài)變化時(shí)，三種算法獲取的最優(yōu)值均出現(xiàn)明顯波動(dòng)，主要原因是原有最優(yōu)解經(jīng)過(guò)動(dòng)態(tài)變化后變成次優(yōu)解，本文算法可在最快時(shí)間內(nèi)尋找最優(yōu)解。隨著進(jìn)化次數(shù)的增加，適應(yīng)度值呈下降趨勢(shì)，說(shuō)明本文算法可有效利用前期優(yōu)化結(jié)果，加快獲取最優(yōu)解速度。本文算法自動(dòng)控制群體動(dòng)畫(huà)行為通過(guò)較少進(jìn)化次數(shù)即可實(shí)現(xiàn)有效的自動(dòng)控制，驗(yàn)證本文算法控制群體動(dòng)畫(huà)行為的有效性，本文算法控制過(guò)程中可有效跟蹤群體動(dòng)畫(huà)內(nèi)動(dòng)態(tài)環(huán)境變化，收斂速度明顯優(yōu)于另外兩種算法，說(shuō)明本文算法具有較好的自適應(yīng)能力，且獲取的適應(yīng)度值與全局最小值較為接近。

統(tǒng)計(jì)本文算法收斂至全局最優(yōu)解后，周?chē)h(huán)境發(fā)生10次變化時(shí)，本文算法重新收斂至全局最優(yōu)解進(jìn)化次數(shù)，并將本文算法與Q?學(xué)習(xí)算法以及目標(biāo)跟蹤算法對(duì)比，結(jié)果如表1所示。

由表1實(shí)驗(yàn)結(jié)果可以看出，本文算法在自動(dòng)控制群體動(dòng)畫(huà)內(nèi)個(gè)體移動(dòng)至圈內(nèi)以及移動(dòng)至看臺(tái)行為的進(jìn)化次數(shù)均明顯小于Q?學(xué)習(xí)算法以及目標(biāo)跟蹤算法，說(shuō)明本文算法可較快收斂至全局極值，有效驗(yàn)證了本文算法具有優(yōu)秀的尋優(yōu)性能。

微粒群算法內(nèi)種群多樣性可令環(huán)境發(fā)生改變時(shí)算法內(nèi)粒子仍可覆蓋搜索大空間面積，為微粒群算法尋找新的全局最優(yōu)值提供支持，可改善粒子過(guò)度收斂令算法陷入局部最優(yōu)值情況。采用本文算法自動(dòng)控制群體動(dòng)畫(huà)內(nèi)個(gè)體移動(dòng)至圈內(nèi)行為時(shí)尋找全局最優(yōu)解過(guò)程中群體多樣性如圖7所示，將本文算法與Q?學(xué)習(xí)算法以及目標(biāo)跟蹤算法對(duì)比。

本文算法在自動(dòng)控制群體動(dòng)畫(huà)內(nèi)個(gè)體移動(dòng)至看臺(tái)行為時(shí)尋找全局最優(yōu)解過(guò)程中群體多樣性如圖8所示，將本文算法與Q?學(xué)習(xí)算法以及目標(biāo)跟蹤算法對(duì)比。

通過(guò)圖7，圖8實(shí)驗(yàn)結(jié)果可以看出，本文算法在自動(dòng)控制群體動(dòng)畫(huà)內(nèi)個(gè)體移動(dòng)至圈內(nèi)以及移動(dòng)至看臺(tái)行為過(guò)程中種群多樣性明顯優(yōu)于另兩種算法，說(shuō)明本文算法具有較高全局搜索性能，本文算法應(yīng)用于群體動(dòng)畫(huà)自動(dòng)控制中控制性能較高。

3? 結(jié)? 語(yǔ)

本文算法將微粒群優(yōu)化算法應(yīng)用于群體動(dòng)畫(huà)行為自動(dòng)控制中，依據(jù)全局極值情況判定個(gè)體周?chē)欠翊嬖谧兓?dāng)存在環(huán)境變化時(shí)，需要將部分微粒重新初始化，令種群搜索范圍擴(kuò)大，提升微粒種群多樣性，通過(guò)微粒具有的記憶功能，避免微粒群陷入局部最優(yōu)情況，令群體動(dòng)畫(huà)行為自動(dòng)控制效果更高。通過(guò)實(shí)驗(yàn)驗(yàn)證該算法自動(dòng)控制群體動(dòng)畫(huà)行為有效性，該算法可依據(jù)用戶(hù)意愿自動(dòng)控制群體動(dòng)畫(huà)內(nèi)個(gè)體依據(jù)運(yùn)動(dòng)軌跡運(yùn)動(dòng)，實(shí)現(xiàn)運(yùn)動(dòng)目標(biāo)跟隨效果，采用該算法自動(dòng)控制的群體動(dòng)畫(huà)行為具有真實(shí)感強(qiáng)、控制性能良好的優(yōu)勢(shì)。

參考文獻(xiàn)

[1] 許奇，王華彬，周健，等.用于目標(biāo)跟蹤的智能群體優(yōu)化濾波算法[J].智能系統(tǒng)學(xué)報(bào)，2019，14（4）：697?707.

[2] 張峰，劉凌云，郭欣欣.基于改進(jìn)Q?學(xué)習(xí)算法的多階段群體決策模型[J].控制與決策，2019，34（9）：1917?1922.

[3] 徐選華，楊玉珊，陳曉紅.基于決策者風(fēng)險(xiǎn)偏好大數(shù)據(jù)分析的大群體應(yīng)急決策方法[J].運(yùn)籌與管理，2019，28（7）：1?10.

[4] 那赟，栗繼祖，馮國(guó)瑞.群體認(rèn)知對(duì)個(gè)體不安全行為意向的跨層次影響[J].中國(guó)安全科學(xué)學(xué)報(bào)，2019，29（2）：13?19.

[5] 孫劍，張磊，董建軍，等.隧道工人群體心理資本對(duì)群體行為的影響[J].土木工程與管理學(xué)報(bào)，2019，36（5）：19?24.

[6] 趙越，蒙毅，李仁義.基于粒子群優(yōu)化算法分析約束條件對(duì)配煤最優(yōu)價(jià)格的影響[J].熱力發(fā)電，2017，46（12）：99?104.

[7] 徐利鋒，黃祖勝，楊中柱，等.引入多級(jí)擾動(dòng)的混合型粒子群優(yōu)化算法[J].軟件學(xué)報(bào)，2019，30（6）：1835?1852.

[8] 戴翠琴，唐煌，郭林峰.衛(wèi)星網(wǎng)絡(luò)中基于雙向?qū)?yōu)粒子群優(yōu)化算法的連接計(jì)劃設(shè)計(jì)[J].通信學(xué)報(bào)，2019，40（8）：189?199.

[9] 張鵬威.采用正弦映射與擴(kuò)張算子的二進(jìn)制粒子群優(yōu)化算法[J].小型微型計(jì)算機(jī)系統(tǒng)，2019，40（6）：1160?1164.

[10] 王碩禾，鄭俊觀，陳祖成，等.基于改進(jìn)粒子群優(yōu)化算法光伏陣列多峰值MPPT的研究[J].可再生能源，2019，37（6）：879?885.

[11] 孫輝，鄧志誠(chéng)，趙嘉，等.混合均值中心反向?qū)W習(xí)粒子群優(yōu)化算法[J].電子學(xué)報(bào)，2019，47（9）：1809?1818.

[12] 王沿朝，陳清軍.基于粒子群優(yōu)化算法的軟土場(chǎng)地Davidenkov模型參數(shù)擬合與應(yīng)用[J].振動(dòng)與沖擊，2019，38（17）：8?16.

[13] 徐偲喆，查曉銳.基于改進(jìn)粒子群優(yōu)化模糊控制的MPPT算法研究[J].電機(jī)與控制應(yīng)用，2019，46（10）：35?39.

[14] 張煜培，趙知?jiǎng)牛嵤随?融合學(xué)習(xí)差分進(jìn)化和粒子群優(yōu)化算法的認(rèn)知決策引擎[J].計(jì)算機(jī)科學(xué)，2019，46（6）：95?101.

[15] 黃文雅.基于改進(jìn)版粒子群優(yōu)化算法的最優(yōu)雙層規(guī)劃模型及其求解[J].統(tǒng)計(jì)與決策，2018，34（1）：88?91.