大規模移動邊緣計算網絡:空間建模及計算吞吐量優化
(中國信息通信研究院,中國北京100191)
作為5G系統中的關鍵技術之一,移動邊緣計算(MEC)可以利用部署在網絡邊緣的服務器為移動用戶提供泛在、低時延的高質量計算服務[1-2],例如多媒體云游戲、增強現實等。相比中心化的云計算,去中心化的MEC能夠顯著降低計算時延、移動用戶能耗以及網絡傳輸復雜度[3-4],適用于未來邊緣智能網絡[5]、大規模物聯網[6]以及點對點網絡[7]等應用場景。
在MEC中,一個研究熱點領域是設計高效能、低時延的移動計算卸載方式,即移動用戶可將其計算任務卸載到MEC服務器中進行計算。文獻[8]提出了一個卸載計算策略,在給定計算時限要求下,通過聯合設計頻譜和計算分配資源來最小化移動用戶的能耗。對于類似的優化目標,文獻[9]給出了基于Lyapunov優化理論的動態優化結果。文獻[10]則將移動計算卸載及資源分配設計問題拓展至車聯網場景。
雖然上述研究工作僅考慮包含一個或幾個邊緣云和用戶的小規模MEC網絡,就能設計出復雜但有效的計算卸載方案或策略,但是研究并設計并優化大規模MEC網絡(包含無限多個邊緣云和用戶的MEC網絡)中的無線通信和邊緣計算的性能指標也同樣重要。文獻[11]首次提出了基于隨機幾何理論的大規模MEC網絡模型,并對MEC網絡的傳輸時延和計算時延進行了理論分析以及優化設計,為大規模MEC網絡部署提供了重要設計指南;但該文獻并未研究如何定義并最優化地設計MEC網絡空間吞吐量的問題。
為此,我們提出并定義了大規模MEC網絡中的空間計算吞吐量,并通過優化設計MEC服務范圍半徑以及用戶計算卸載比例,來實現MEC網絡空間吞吐量的最大化,以期為部署大規模MEC網絡提供參考。
1 系統模型及性能指標
考慮一個包含無限多個MEC服務器和移動用戶的大規模MEC網絡(如圖1所示)。
1.1 MEC網絡空間分布
在二維空間內,假設MEC服務器和用戶的位置都服從泊松點過程(PPP)分布,其中MEC服務器位置X∈R2服從密度為 λb的PPP分布Ω={X},用戶位置Y∈R2服從密度為λu的PPP分布Φ ={Y}。
1)多用戶接入模型
將總帶寬資源分為M個正交的子信道{1,2,…,M},每個用戶可以隨機選擇一個子信道將計算任務上傳到MEC服務器進行計算(即計算卸載),選擇同一子信道進行傳輸的多個用戶將產生干擾。令時隙間隔為Ts秒,假設用戶位置及信道狀態在不同時隙相互獨立,并要求每個用戶需要在Ts秒內完成計算任務。
2)MEC服務區域


▲圖1 MEC系統模型

▲圖2 大規模MEC網絡空間分布
1.2 邊緣計算卸載模型
1)計算卸載比例

2)上行信道模型

1.3 計算模型
在計算過程中,主要考慮兩個約束條件:一是時延約束Ts,即每個用戶的計算任務需要在Ts秒內計算完畢;二是能量約束ξ,即每個用戶在每個時隙用于計算的能量不得超過ξ。為便于分析,令ξ=qTs以保證每個用戶均有足夠的能量用于計算卸載。
1)邊緣計算
假設每個MEC服務器的計算能力有限,每當其接收到一個用戶卸載的計算任務(包含?比特數據),便啟動一個虛擬機進行獨立的邊緣計算。對于進行計算卸載用戶,其每個計算任務的時延包括3部分:卸載傳輸時延 Tt、邊緣計算時延 Tc、計算結果下載時延 Td。由于計算結果數據量很小,因此可忽略Td。為滿足時延約束條件,要求Tt+Tc≤Ts。對于卸載傳輸時延 Tt,令用戶數據傳輸速率為η=B ·log2(1+θ),其中B為子信道帶寬,Tt可表示為Tt= ?/η,期間能量消耗為qTt。對于邊緣計算時延 Tc,根據文獻[13]中的計算時延模型,Tt可表示為Tc=T0(1+d)i-1,其中,i為虛擬機數量,d≥0為多個虛擬機的復用退化因子,T0= ?/μec為單個虛擬機計算每個任務的時延(μec是虛擬機計算能力,單位為比特/秒)。
2)本地計算

1.4 性能指標
1)卸載傳輸成功概率
為定量刻畫上傳信道(即卸載傳輸)的可靠性,定義卸載傳輸成功概率p?,s,數學表達式為p?,s=Pr(SIR ≥ θ)。
2)MEC成功概率
首先,為刻畫用戶的計算任務,可以在規定時間Ts內計算完畢的概率pc,數學表達式為pc=Pr(Tt+Tc≤Ts)。考慮到每個用戶可以將計算任務卸載至其附近的W個MEC服務器,當其中任意一個MEC服務器能夠在規定時間內完成計算任務,就意味著該用戶的卸載計算成功。基于此,為衡量MEC服務成功概率,定義MEC成功概率 pmec(W)為pmec(W)=1-(1-pcp?,s)W。
3)MEC網絡空間吞吐量
為刻畫大規模網絡中成功完成計算的用戶空間密度,定義MEC網絡空間吞吐量C=Cec+Clc,其中Cec表示利用邊緣計算完成的吞吐量,Clc表示利用本地計算完成的吞吐量,其數學表達式分別為:

其中,I(A)為指示函數,即當事件A發生時,I(A)為1,否則為0。
結合公式(1)和(2),可以得到C的表達式:

2 對MEC網絡空間計算吞吐量的理論分析
在本節中,我們將對MEC成功概率以及MEC網絡空間計算吞吐量等關鍵性能指標進行分析,為后續對網絡進行優化設計提供理論基礎。
2.1 卸載傳輸成功概率分析


2.2 MEC成功概率分析



基于公式(6),pc下界可表示為:

基于公式(4)和(7),可得到MEC成功概率的下界:

根據公式(3)和公式(8),MEC網絡空間計算吞吐量的下界則可以表示為:


3 對MEC網絡空間計算吞吐量的優化設計
3.1 優化MEC服務范圍半徑

觀察公式(10)并考慮優化r0的物理含義。一方面,當r0變小時(即每個MEC服務范圍變小),每個MEC服務器接收到的卸載計算任務數量會減小,由此將縮短對每個任務的計算時延從而提升MEC成功概率;另一方面,當r0變大時,每個用戶將會被更多的MEC服務器所覆蓋并有更大概率實現MEC,由此MEC成功概率也會提升。因此,我們可以設計最優的r0使C最大化。
由于直接根據公式(10)來優化r0存在一定難度,首先考慮兩種特殊情況下的優化設計,情況1是假設上行信道十分可靠時,以致卸載傳輸成功概 率 為 1(即 p?,s=1),情況 2 是當MEC服務器計算能力很強時,以致卸載任務總能在規定時間內完成計算(即T0→ 0,pc=1)。
首先考慮情況 1,當 p?,s=1,表示為:

其中 c1=λbπ。由于C(low)對r0是可微的,通過優化設計r0來最大化的問題可以表示為P1:


當MEC服務器密度極高時,即λb→ ∞,P1可簡化為P2:

接下來,考慮情況2。當pc=1,可表示為:

優化設計r0的問題可表示為P3:


當MEC服務器密度極高時(即λb→ ∞),P3可簡化為P4:

3.2 優化計算卸載比例
首先考慮通過優化ρ來最大化MEC網絡空間吞吐量C的物理含義。太大或太小的ρ都將會降低C,這是因為:太大的ρ將會引起更嚴重的用戶間干擾和卸載計算任務數量,導致MEC成功概率降低,從而降低C;太小的ρ會直接降低網絡中卸載用戶密度,導致C的減小。因此,可以通過優化ρ來最大化C。
類似3.1節的步驟,首先考慮當上行信道十分可靠時(即p?,s=1),可表示為:


P5為凸優化問題,對P5的最優解 ρ*可通過求解等式(21)得到:
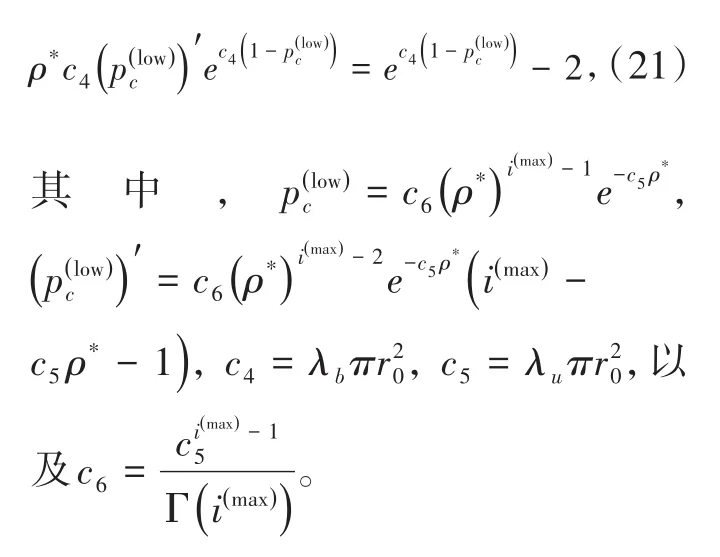



討論3:觀察 ρ*閉式解,當增加時,表示MEC服務器計算能力強,便可提高 ρ*以加大卸載用戶數目,來提高網絡計算吞吐量;當用戶密度λu增加時,則應減小 ρ*以減輕MEC服務器計算壓力,從而保證一定的MEC成功概率。
接下來,考慮當MEC服務器計算能力很強(即pc=1),C(low)可表示為:

基于公式(23),對于 ρ*的最優化問題可設計為P7:

對P7的最優解 ρ*可通過求解等式(25)得到:

當MEC服務器密度極高時(即λb→∞),P7可簡化為如下優化問題:


4 仿真結果
在本節中,我們利用MATLAB仿真對上文中得到的理論結果加以驗證,主要仿真參數設置如下:λb=0.01/m2,λu=0.1/m2,r0=8m,ρ=0.7,θ=10dB,B=3kHz,α =3,Ts=100ms,? =103bits,T0=1ms,d=0.3。其中,蒙特卡洛仿真結果由圓圈表示,理論分析結果由實/虛線表示。限于篇幅,這里只展示最重要的3個仿真結果。
圖3展示了典型用戶的MEC成功概率,其中,虛線表示用戶將計算任務只卸載到任意一個服務器時MEC成功概率,實線則表示用戶將計算任務卸載到附近的W個服務器時的MEC成功概率,即公式(8)。首先,文中得到的理論結果(下界)與仿真結果之間的差值較小,這證明理論結果比較準確;其次,可以觀察到,相比選擇一個MEC服務器進行計算卸載,當用戶選擇向W個服務器同時進行計算卸載時的MEC成功概率有明顯提升,這得益于宏分集增益。

▲圖3 MEC成功概率與計算卸載比例關系圖

▲圖4 MEC網絡空間吞吐量與MEC服務區域半徑關系圖
圖4展示了通過優化r0來最大化MEC網絡吞吐量C。首先,文中我們所求得的C(low()下界)相比C僅有少量差值,這表示理論下界較為準確;其次,當給定ρ的值,C及C(low)是變量r0的凹函數,因此可以通過設計最優的來最大化C,如當ρ在0.5~0.7之間時在8~9 m之間。另外,當提高ρ的值,C的最大值會隨之變大,這是因為增大ρ意味著更多的用戶選擇計算卸載,從而有效增大網絡吞吐量。
圖5展示了通過優化ρ來最大化MEC網絡吞吐量C。給定r0,C及C(low)同樣是變量ρ的凹函數。當r0在8~10 m之間時,最優值ρ*在0.5~0.7間。另外,當r0增大時,MEC服務范圍將擴大,更多用戶的計算任務可卸載至服務器;因此,網絡吞吐量也會增加。

▲圖5 MEC成功概率與計算卸載比例關系圖
5 結束語
本文中,我們首次定義了大規模MEC網絡中的空間計算吞吐量這一性能指標,并通過優化設計MEC服務范圍半徑r0以及用戶計算卸載比例ρ這兩個指標,實現MEC網絡空間吞吐量的最大化。所提供的理論分析與優化結果將為部署大規模MEC網絡提供了極為重要的設計參考。

