圓錐曲線中非對稱代數式的處理方法

施利強 江戰明

摘? ? 要：2019年浙江省高考數學卷圓錐曲線題的處理過程中，出現不能直接用韋達定理處理的非對稱代數式.對于該問題，教師可借助對稱式[y1+y2，y1y2，y1-y2，y1y2+y2y1]，化非對稱代數式為對稱式[y1=12（y1+y2+y1-y2）]，[y2=12[（y1+y2）-y1-y2]].從而將任意的非對稱代數式[my1+ny2]化為對稱式[my1+ny2=λ（y1+y2）+μy1-y2）]，最終可以用韋達定理解決.

關鍵詞：高考;圓錐曲線;非對稱代數式

2019年浙江省高考數學卷圓錐曲線題的處理過程中，出現不能直接用韋達定理處理的非對稱代數式.筆者開設了一堂關于圓錐曲線中非對稱代數式處理的公開課，對該問題進行了探討.筆者考慮到圓錐曲線題型的代數運算量和課堂的可操作性，本堂課圍繞一個橢圓模型展開.

一、非對稱問題的引入

（一）課堂引入，模型建立

在課堂的引入部分，針對2019年高考的圓錐曲線題，筆者給出兩個探究問題，讓學生一起探究.

探究一：如圖1，已知點[P]為橢圓[x24+y23=1]上一個動點，問：[kPA1kPA2]是否為定值？

解析：A1（-2，0），A2（2，0）設[P（x0，y0）]，[kPA1kPA2=y0x0+2?y0x0-2=y20x20-4]，由[P（x0，y0）]在橢圓上即[x204+y203=1]，代入消元化簡得：[kPA1kPA2=-34].

【評注】學生的證明過程用到點在曲線上這個條件，這也是我們處理圓錐曲線參數問題的常用消元方法.

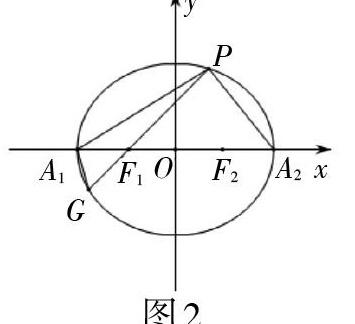
探究二：如圖2，過點[P]與左焦點[F1]作焦點弦[PG]，并連接[A1G]，問：[kPA1kGA1]是否為定值？

解析：設[lPG：x=my-1].與橢圓方程聯立： [（4+3m2）y2-6my-9=0]，得到：

[y1+y2=6m4+3m2y1y2=-94+3m2]，同時算得：

[x1+x2=-84+3m2x1x2=4-12m24+3m2].當然，化簡的過程用到[x1=my1-1，x2=my2-1]，即點在直線上消元.最后得出結論：[kPA1kGA1=y1y2（x1+2）（x2+2）=-94]，是一個定值.

其中，代入直線消元也是我們處理圓錐曲線參數問題的常用方法.

問題：結合剛才探究一的結論：[kPA1kPA2=-34]，是否可以得到[kPA2，kGA1]之間的關系？

解答：兩個式子作除法，可以得到：[kPA2kGA1=13]，即斜率的比值是一個定值.

【評注】通過這兩個探究，讓學生回顧在解決圓錐曲線問題時常用的兩種處理方法：點代入曲線消元和代入直線消元.另一方面，在回顧舊知識的同時，引出本節課主要的橢圓模型，并得到模型中斜率的比值的定值關系，為下文引出本節課的主題做好鋪墊.

（二）深入探究，引發沖突

引入部分借助于已知的常用結論，得到[kPA2，kGA1]之間滿足的關系式[kPA2kGA1=13]，如果直接探究，是否也可以順利得到該關系式？

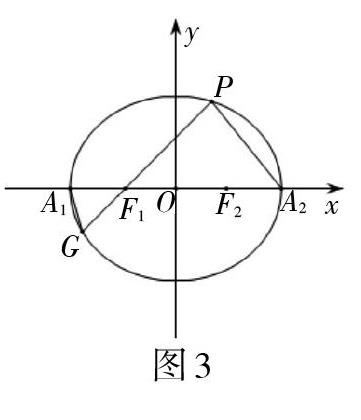
問題重述：如圖3，過點[P]與左焦點[F1]作焦點弦[PG]，連接[PA2]，[A1G]，問：[kPA2kGA1]是否為定值？

解析：設[P（x1，y1），G（x2，y2）]， [kPA2kGA1=y1y2?x2+2x1-2]，再由點在直線上[x1=my1-1，x2=my2-1]，消元得到：[kPA2kGA1=y1y2?x2+2x1-2=y1y2?my2+1my1-3=my1y2+y1my1y2-3y2].

一般能用韋達定理解決的代數結構式是對稱式：[y1+y2，y1y2，y1-y2，y1y2+y2y1].此時我們發現，這里的目標式是非對稱代數式，不能很順利地由韋達定理解決.但是由前兩個探究我們可以知道，代數式的結果是一個定值[13].具體如何求？

【評注】深入探究，通過點代入直線消元化簡代數式，發現目標式不能用韋達定理直接解決，從而引發沖突.同時，由于代數結構的非對稱，提出非對稱代數式，并強調能用韋達定理解決的對稱式：[y1+y2，y1y2，y1-y2，y1y2+y2y1].

二、非對稱問題解決方法探究

方法1：化非對稱式為對稱式

我們知道常用對稱式有：[y1+y2，y1y2，y1-y2，y1y2+y2y1]，如果還是想要化非對稱代數式為對稱式，是否可以將目標式轉化為這些對稱式，從而利用韋達定理解決.比如最簡單的非對稱式[y1]，是否可行？

解析： 假設[y1>y2]，就得到對稱式：[y1=12（y1+y2+y1-y2）].同理可以得到關于[y2]的對稱式：[y2=12[（y1+y2）-y1-y2]].

由本題圖形的對稱性，以下我們都假設[y1>y2].此時，對于任意關于[y1，y2]的線性結構：[my1+ny2]，代入[y1，y2]的對稱式或者利用待定系數法，都可以得到對稱式：[my1+ny2=λ（y1+y2）+μy1-y2）].這樣任意的非對稱代數式都可以化成對稱式，最終利用韋達定理化簡求解.

回到原問題：[kPA2kGA1=my1y2+y1my1y2-3y2]，假設[y1>y2]，利用[y1，y2]的對稱代數式，[y1=12（y1+y2+y1-y2）]，[y2=12[（y1+y2）-y1-y2]]，[y1-y2=121+m23m2+4]分別得到：[my1y2+y1=14+3m2[-6m+61+m2]]，[my1y2-3y2=14+3m2[-18m+181+m2]]，則[kPA2kGA1=my1y2+y1my1y2-3y2=13]，并將學生的結果投屏.

【評注】借助對稱式[y1+y2，y1y2，y1-y2，]

[y1y2+y2y1]，化非對稱代數式為對稱式：[y1=12（y1+y2+y1-y2）]，[y2=12[（y1+y2）-y1-y2]].從而可以將任意的非對稱代數式[my1+ny2]化為對稱式[my1+ny2=λ（y1+y2）+μy1-y2）]，最終可以用韋達定理解決.另一方面，這里化非對稱代數式為對稱代數式，將分子、分母都化成以[m]為主元的代數式，所以選定主變元也很重要.

方法2：利用點在曲線上化對稱

方法1消元的時候利用的是點在直線上消元，是較常用的消元方法.本題由于代數式結構的特殊性，還可以利用點在曲線上消元，從而達到化對稱的目的.由于該方法的特殊性，直接給學生作演示.

解析：[k1k2=y1y2?x2+2x1-2]，兩邊平方得：[k21k22=y21y22?（x2+2）2（x1-2）2]，由于[x214+y213=1]，[x224+y223=1]，消去[y1，y2]，并化簡得：[k21k22=1-x2141-x224?（x2+2）2（x1-2）2]

[=（4-x21）（4-x22）?（x2+2）2（x1-2）2]

[k21k22=（x1+2）（x1-2）?（x2+2）（x2-2）=]

[x1x2+2（x1+x2）+4x1x2-2（x1+x2）+4][=19]，結合圖象可得，[k1k2=13].

【評注】利用點在曲線上消元，一方面與課前的復習內容相呼應.另一方面，將非對稱代數結構化為對稱式，從而可以用韋達定理解決.進而說明化非對稱式為對稱式方法的多樣性，也為突出方法1的優勢做鋪墊.

三、變式訓練? ?感受方法

通過剛才的探究，學生已經學到幾種處理非對稱問題的方法，相對來說，學生覺得方法1利用[y1=12（y1+y2+y1-y2）]，[y2=12[（y1+y2）-y1-y2]]化非對稱式為對稱式實用一點.作為該方法的鞏固，接下來在原來橢圓模型的基礎上提出以下變式訓練，并選取部分學生的結果進行投屏探討.

變式1：如圖4，已知橢圓[x24+y23=1]，[AB]為過左焦點[F1]的焦點弦，點[A]在[x]軸上方，求[2F1A+1F1B]的取值范圍.

解析：[F1A=1+m2y1]，[F1B=1+m2y2]，

[2F1A+1F1B=11+m2（2y1+1y2）][=11+m2（2y1-1y2）=11+m22y2-y1y1y2][=2-13m1+m2 ][∈53，73].

【評注】在前面模型的基礎上做變式訓練，讓學生進一步了解用該方法在解決非對稱問題時要注意的地方.并在訓練中讓學生慢慢掌握這種處理非對稱問題的方法，體會該方法在處理非對稱問題時的優勢.

變式2：如圖5，已知橢圓[x24+y23=1]，[AB]為過左焦點[F1]的焦點弦，點[A]在[x]軸上方，求[2F1A+F1B]的取值范圍.

解析1：[2F1A+F1B][=1+m2（2y1-y2）]，

[2y1-y2=12（y1+y2）+32（y1-y2） ，][2F1A+F1B=1+m2?3m-181+m24+3m2].

解析2：由橢圓極坐標公式：[F1A=ep1-ecosθ]，[F1B=ep1+ecosθ]

（其中[e=12]，[p]為焦準距，[p=b2c=3]）

[1F1A+1F1B=2ep][=43].其中[F1A∈（a-c，a+c）=（1，3）]

[2F1A+F1B][=34?（2F1A+F1B）?（1F1A+1F1B）][=34?（3+F1BF1A+2F1AF1B）]

令：[F1AF1B=t]，[t∈13，3]，則[2F1A+F1B=34（3+1t+2t）∈][94+322，7]

【評注】從變式2也可以看到，本題目標式也是非對稱式，但今天的方法也不一定是萬能的，解析1雖然能將目標式用主變量[m]表示，但是結果也不一定容易計算，這時候需要選取合適的方法來解決，解析2利用極坐標公式順利地解決了該問題.當然該類化非對稱式為對稱式題型的核心還是統一變量，不同的題化對稱式選取的主變量可能也會不同.

四、拓展延伸? ?鞏固提高

最后給出基于本節課模型的幾個思考題，希望學生能對該類非對稱式題型的處理方法有更進一步的感悟.

例題：已知橢圓[x24+y23=1]，點[P]為橢圓上的一個動點，[A1，A2]分別為左右頂點.

思考題1：如圖6，[PG]為過左焦點[F1]的焦點弦，分別過P，[A2]與G，[A1] 作直線[PA2]，[GA1]交于點[T]，證明：點[T]落在定直線上.

思考題2：如圖7，點[Q（m，0）]是橢圓長軸上異于左右焦點的定點，連接[PQ]并延長交橢圓于點[G]，分別過P，[A2]與G，[A1] 作直線[PA2]，[GA1]交于點[T]，證明點[T]的橫坐標為定值.

思考題3：如圖8，點[Q（m，0）]是橢圓長軸外的定點，連接[PQ]交橢圓于點[G]，分別過P，[A1]與G，[A2] 作直線[PA1]，[GA2]交于點[T]，證明點[T]的橫坐標為定值.

【評注】本節課的最后，為了讓學生能進一步體會并掌握該處理方法，提出本課模型下的三個思考題，從而達到拓展學生的思維、鞏固舊知識、提高學生能力的作用.

五、總結升華? ?感悟提升

本堂課筆者以一個橢圓模型貫穿始末，由我們的常見結論引出橢圓中的非對稱式的問題，在復習舊知的同時引出非對稱式的問題.通過層層引導，得出解決該類問題的主要方法是化非對稱式為對稱式，并強調轉化過程中得注意主變量的選取，最終利用韋達定理得以解決.當然解決該類問題的方法很多，通過練習也發現該方法并不是萬能的，得看具體情況選取解決方法.最后提出的三個思考題也是非對稱式問題，其背景是極點極線理論，是否以該理論為背景的題較多會出現非對稱目標式有待我們進一步挖掘.另外，雙曲線和拋物線中也有類似的非對稱式問題，針對不同圓錐曲線類型，是否還有其他處理方法，有待我們進一步探究.