利用基本信息和行為數據發現高校貧困學生

聶 敏，張 楊，鄧 輝，王 偉，夏 虎，周 濤

(電子科技大學大數據研究中心 成都 611731)

近年來，高校領域的大數據應用研究工作越來越受到各方關注[1-16]。為了評判學生在校期間的表現，文獻[5]在2012 年率先將數據挖掘技術應用于高校數據。2014 年，文獻[6]繼續深入研究了這個方向，將更多的數據用于評判學生的學業。后續，學者利用大數據分析手段，繼續深入研究了學生行為對成績或職業的影響[7-15]。這些研究都將目的定位于學生學業或職業選擇，未關注學生家庭的經濟情況。高校學生的培養，一直是國家和社會高度關注的。在培養高校人才的戰略中，每年的教育支出也在逐步上漲。其中，相當一部分的支出會用于家庭貧困的學生，以幫助其順利完成學業。目前高校對于家庭貧困學生的認定工作存在著不少漏洞，過程也非常繁瑣低效，沒有達到精準資助的要求。在當下的大數據時代，如何利用多維學生數據分析學生的家庭貧困信息是非常有必要的。

本文以學生行為數據為基礎，利用大數據挖掘的相關技術，構建了家庭貧困學生挖掘算法，為高校扶貧工作提供支持。所謂家庭貧困學生挖掘，即基于學生在學校中的消費數據和其他行為數據，預測其家庭經濟條件：是否存在困難。根據高校學生數據的維度豐富和時序性特點，本文抽取了學生基本信息的統計特征和行為數據的時序性特征，提出了深度學習算法(clockwork recurrent neural network,CW-RNN)的改進方法CW-LSTM，用于評估學生的各維度特征，綜合判定其經濟條件。最后，本文利用某高校2011～2014 級學生在2012 年?2015 年產生的數據進行分析，驗證了本文方法的有效性。

1 CW-LSTM 算法框架

神經網絡結構已經應用在AI 領域的各個方面，在研究之初，為了將以往的信息連接到當前的任務中，研究者在網絡結構中引入了循環結構，即RNN。其計算方式為：

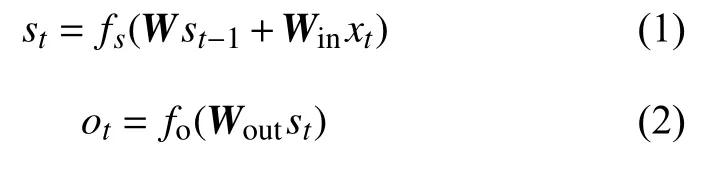
式中， x是輸入；Win為輸入層矩陣；W 是隱藏層矩陣；Wout為輸出層矩陣； s是隱藏層輸出； o是輸出層輸出； fs為隱藏層激活函數； fo為輸出層激活函數。通過 st?1～ st的循環結構實現信息的復用。但是RNN 網絡僅能記憶短期信息，對于長時間序列，會造成信息丟失。為了解決這樣的信息丟失，文獻[17]提出了改進的算法—CW-RNN。CWRNN 將隱含層分為多個模塊，并對每個模塊設定時間頻率，以便每個模塊的單獨管理。在每個模塊內部進行全連接，在模塊間進行高時鐘頻率模塊向低時鐘頻率模塊的連接，如圖1 所示。Hidden 表示隱藏層。在隱藏層中，多個模塊的時間頻率為T1, T2···, Tg。體現在公式中為：將 W與 Win分為g塊。

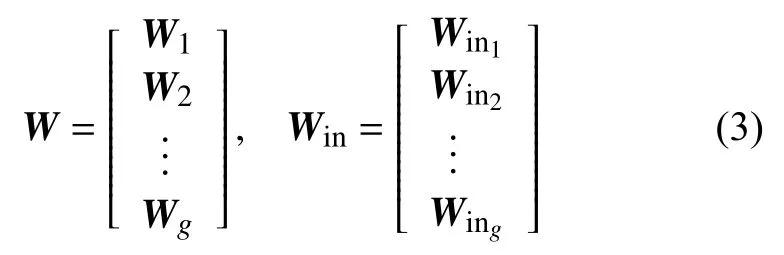
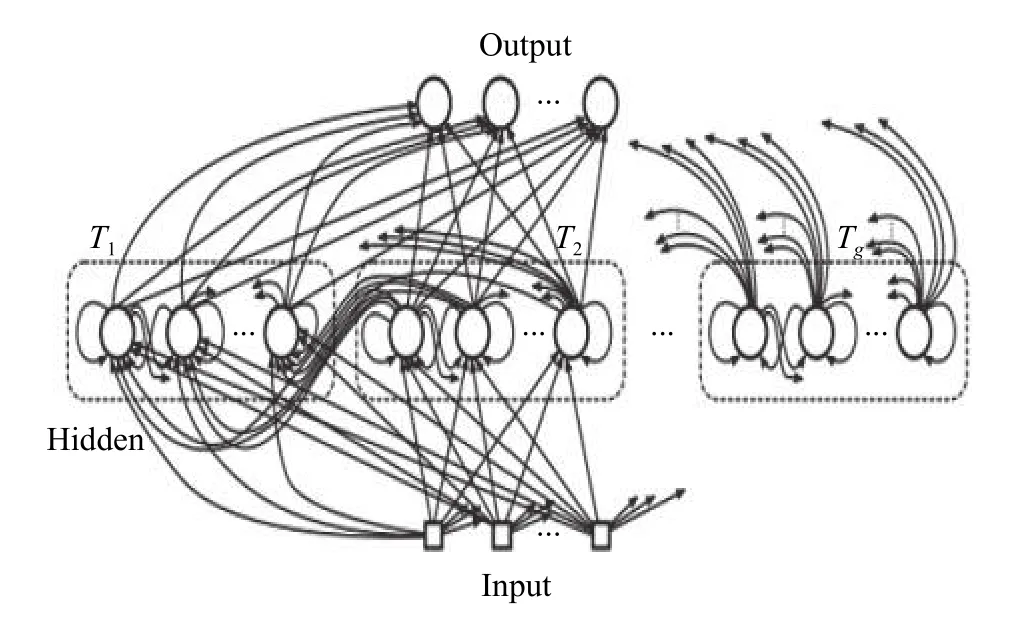
圖1 CW-RNNs 網絡結構

在運算的時候，只會有部分模塊參與運算，不參與運算的模塊就置為0，實現了對長短時間的處理。

LSTM 也可以部分解決RNN 的長時間序列信息丟失問題[18]。在LSTM中，每個神經元都是一個細胞，在每個細胞中，都包含存儲器和3 個門：輸入門、輸出門和遺忘門。輸入門決定了哪些新的輸入信息加入到存儲器，遺忘門決定了從存儲器中丟失哪些信息，輸出門決定了每個狀態的輸出值。其單一神經元的結構如圖2所示。其中， xt表示t時刻的輸入， st?1表示t ?1時刻的輸出， ht?1表示t ?1時刻的細胞狀態， st表示t時刻的輸出， ht表示t時刻的細胞狀態。

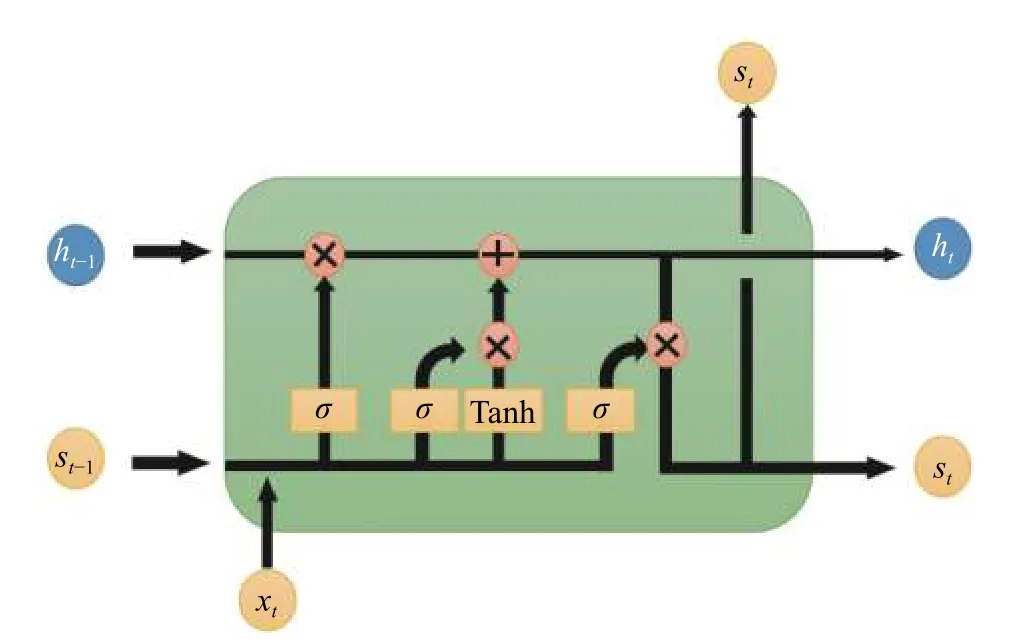
圖2 LSTM 的細胞結構示意圖

在每個細胞中，首先計算遺忘門：

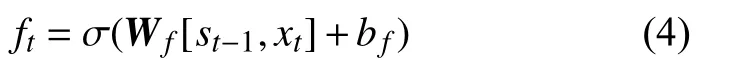
式中， σ是sigmoid 激活函數，具體表示為：

Wf是遺忘門的權重矩陣； bf是遺忘門的偏置。然后計算輸入門：

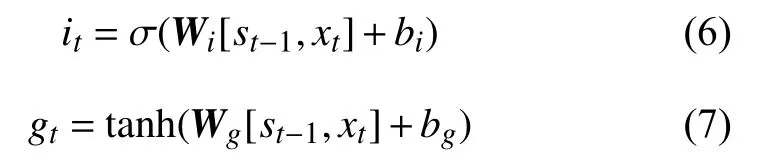
式中，tanh是tanh激活函數，具體表示為：

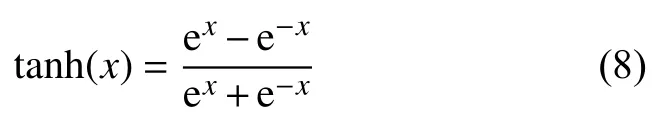
Wi、 Wq都是權重矩陣； bi、 bq都是偏置。通過式(4)～式(6)可以更新細胞狀態為：

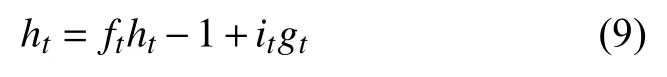
最后計算輸出門：

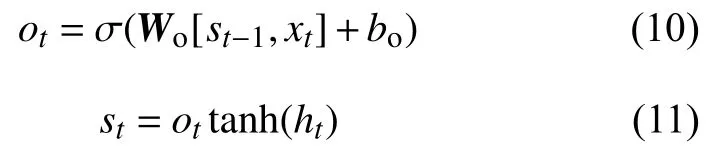
式中，Wo是輸出門權重矩陣； bo是輸出門偏置。模型最終訓練的就是所有的權重矩陣和偏置。

CW-RNN 網絡的設計簡單，層次清晰，但其表達能力不強，容易出現高偏差的情況。而LSTM算法結構復雜，表征能力強，但是其參數多，訓練復雜度高，有些超參數(即不能通過訓練得到的參數值，如網絡隱藏層數、迭代輪數等)需要人工提前配置，如果超參數設置不合理，其性能也會受到較大影響。為了結合兩種算法各自的優點，本文提出兩種算法的融合算法—CW-LSTM。CW-LSTM算法保留LSTM 中的輸入門和輸出門，而對于其處理長時間依賴的遺忘門，使用CW-RNN 網絡的多模塊管理和高時鐘頻率模塊向低時鐘頻率模塊里的連接來實現。

在CW-LSTM 算法中，每個存儲塊中包含存儲器、輸入門和輸出門。對每個存儲塊內部按照CW-RNN 網絡的方式進行構建，將存儲器設置為多個，并且配置不同的時鐘頻率，然后進行分組管理，不同存儲器之間由高時鐘頻率向低時鐘頻率進行連接。圖3 展示了單個存儲塊的結構，其構建了一個4 個周期的CW-LSTM 存儲塊。利用多個這樣的存儲塊，就可以構建CW-LSTM 網絡。對于CW-LSTM 的計算，輸入門和輸出門的計算方式與LSTM 一樣，對于狀態的管理，和CW-RNN一樣，將狀態權重矩陣分為g 個模塊，運算的時候只有高時鐘頻率向低時鐘頻率的連接模塊才會進行計算。

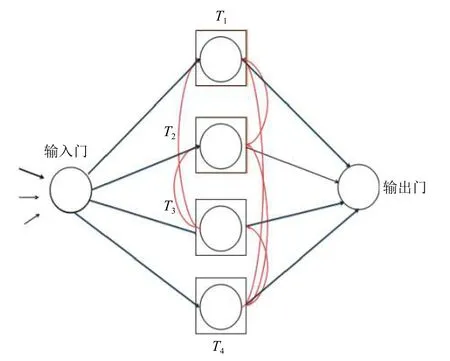
圖3 CW-LSTM 存儲塊結構

本文也對3 種網絡結構的訓練參數個數和效率進行了計算。假設CW-RNN、LSTM 和CW-LSTM 3 種網絡的隱藏層數都為M，對于CW-LSTM和CW-RNN，周期為R，每個分組內節點數量為N，則有M=RN。用O 表示網絡中需要訓練的參數個數，3 種網絡表示為：

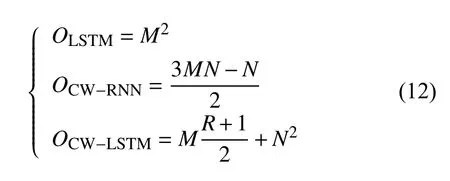
可以看出，3 種網絡結構的時間復雜度都為O(M2)，CW-LSTM 網絡計算效率介于兩者之間。

2 基于CW-LSTM 的家庭貧困學生挖掘模型

針對高校學生統計數據的豐富維度和行為數據的時序性特點，本文針對性地抽取了多個特征進行研究。最后將處理好的特征輸入到CW-LSTM 模型中進行貧困預測。所有的數據均是在匿名的條件下采集和試用。

2.1 特征提取

基本統計特征是利用數理統計技術獲取的一些基本特征。在學生基本信息上，本文考慮性別、生源地、民族和年級4 個維度的特征。在消費數據中，根據獲得的數據分布以及學生在校期間的消費范圍，將消費數據分為食堂消費數據和其他消費數據，食堂消費數據包含早餐、中餐、晚餐和宵夜，其他消費數據包含超市、洗澡、洗衣等非食堂消費。另外，再將消費數據細分為消費次數、消費平均值和最大值。還提取了其他數據特征，如圖書館門禁、寢室門禁、成績和寒暑假留校情況。

抽象特征的構建是結合家庭貧困學生挖掘的目標和相關業務人員的工作經驗所提出的。主要包括規律性和朋友圈經濟水平。規律性可以通過一個人特定時段間隔行為發生的熵來描述。假設時間間隔為n，即T ={t1,t2···,tn}，任何一個學生的行為在ti時間間隔發生的概率的計算公式為：

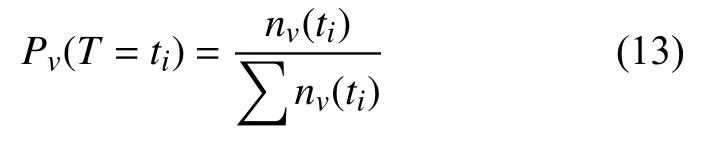
式中，nv(ti)是行為v在時間間隔ti內發生的頻率。則行為v的熵為：

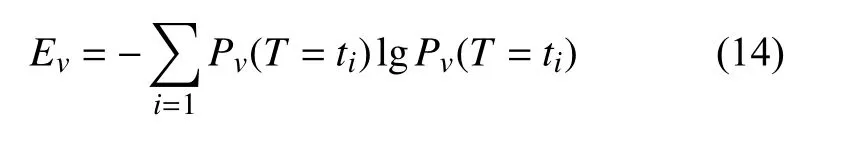
一種行為的熵越高，那么該行為在不同時間段內發生的概率越不均勻，也就是這個行為的規律性較低。在本文的研究中，考慮了食堂就餐、非食堂消費和去圖書館這3 種行為的熵。

對于現在的高校學生，朋友圈能夠反應相當多的信息，而一個人的經濟水平可能會與其朋友圈平均經濟水平相關。首先，引入親密度的概念，其表示兩個人的關系密切程度。然后計算任意兩個學生的親密度RA(B)，設置閾值H，認為與A 親密度大于H 的同學B(RA(B)>H)就是A 的朋友。以此構建朋友圈。對于親密度，可以通過兩個人在某一時間段內同時出現在相同地點的次數來計算，并且不同的刷卡場景需要有不同的權重。學生A 與學生B 在時間周期T 內的親密度計算公式為：

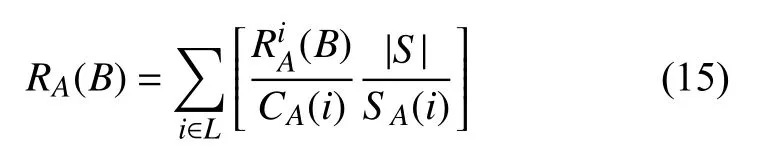
式中， L表示所有的刷卡地點；CA(i)表示在時間周期 T以內，學生A 在地點i的總刷卡次數；RA(B)表示在時間周期T 內，學生A 與學生B 在地點i 的共同出現次數； |S|表示學生總數；SA(i)表示與學生A 在地點i 共同出現的總人數。可以看出，親密度是有向的，A 對于B 的親密度很高并不意味著B 對于A 的親密度就一定很高，即在式(15)中RA(B)?RB(A)。基于式(15)，可以計算任意兩個學生A 和B 的親密度RA(B)，并設定閾值H，認為滿足RA(B)>H要求的學生B 是A 的朋友——這樣就可以得到學生A 的朋友圈。接下來通過學生朋友圈中獲得過助學金的學生數量，以及該學生的朋友數量來定義朋友圈經濟水平 FA，有：

式中， NA代表學生A 的朋友總數； PA代表A 的朋友中家庭貧困的朋友數。

2.2 特征選擇和模型結構

本文進行了特征的提取，但是提取出的特征并不都是有用的，這主要是因為，有些特征非常稀疏，不利于后序的計算。還有些特征之間具有很強的關聯性，導致多種特征只需要其中一種或幾種就能夠達到想要的結果。因此有些特征就變得冗余了，需要進行特征選擇。本文采用后剪枝的C4.5算法進行特征選擇，即首先將數據劃分為訓練集和驗證集，在訓練集上用C4.5 算法生成決策樹，然后進行剪枝。具體操作為：對每一個非葉子節點來說，刪除以此節點為根節點的子樹，讓這個節點變為葉子結點，該葉子節點對應的類別為相應訓練數據中占優的類別。如果這樣操作在驗證集上的準確率沒有比原來的差，就將此節點設置為葉子節點，刪除此節點以下的所有特征。

在經過特征抽取和特征選擇后，得到了高校學生數據的一系列特征。將得到的特征按照{月, 學期}的時間周期進行分組，然后將其輸入到CWLSTM 的不同分組中，完成算法的輸入層構建。在隱藏層中，構建全連接網絡，并且網絡的神經元數量與輸入層相同。最后，在輸出層設置一個輸出神經元，其內部不同周期的存儲器表示不同時間周期的預測結果，然后通過不同的權重連向輸出門，得到最終的預測結果。

3 實驗結果

以某高校2011～2014 級學生為例，對家庭貧困學生挖掘模型進行驗證。獲取到學生基本信息數據32 318 條，消費數據約1.6 億條，圖書館門禁數據1 400 余萬條，寢室門禁數據2 800 余萬條，成績數據近200 萬條，助學金信息數據8 889 條。在式(15)中，時間周期T 統一取為一月。在親密度計算中，將閾值H 設置為0.35。本文將所有的數據隨機劃分為訓練集(80%)和測試集(20%)，在特征選擇階段，選用后剪枝的C4.5 算法獲得的有用特征如表1 所示。

表1 剪枝后的特征

得到最終的特征后，將助學金信息作為訓練標簽，即認為獲得助學金的學生為家庭貧困學生，沒有獲得助學金的學生為家庭非貧困學生，共有家庭貧困學生20 070 名，家庭非貧困學生18 731 名。對于測試數據的所有特征，將其輸入到2.2 節所述的CW-LSTM 模型結構中，設置迭代輪次為1 000。在模型對比中，本文選擇樸素貝葉斯算法和C4.5 決策樹算法。

由于本文采用的是回歸算法，最后模型的輸出結果是一個連續值，表示這個學生屬于家庭貧困學生的概率。本文將這個概率從大到小排序，取前f 的樣本，作為預先設定為家庭貧困學生的人數占比。準確率即為前f 樣本中的確是家庭貧困的學生比例。當f 較小時，表示僅取預測為家庭貧困學生概率較大的樣本，因此其準確率比較高。從圖4 可以看出，當f>0.1 時，CW-LSTM 算法的準確率優于樸素貝葉斯算法和決策樹算法。

對于分類問題，AUC 值也是一個常見的評價指標，即ROC(receiver operator curve)曲線下的面積[18-19]。本文也對家庭貧困學生分類問題的AUC值進行了計算。結果顯示，樸素貝葉斯算法的AUC 值為0.64，決策樹算法的AUC 值為0.652，而本文提出的CW-LSTM 算法的準確率為0.659，同樣也說明CW-LSTM 算法的效果是要優于決策樹算法和樸素貝葉斯算法的。

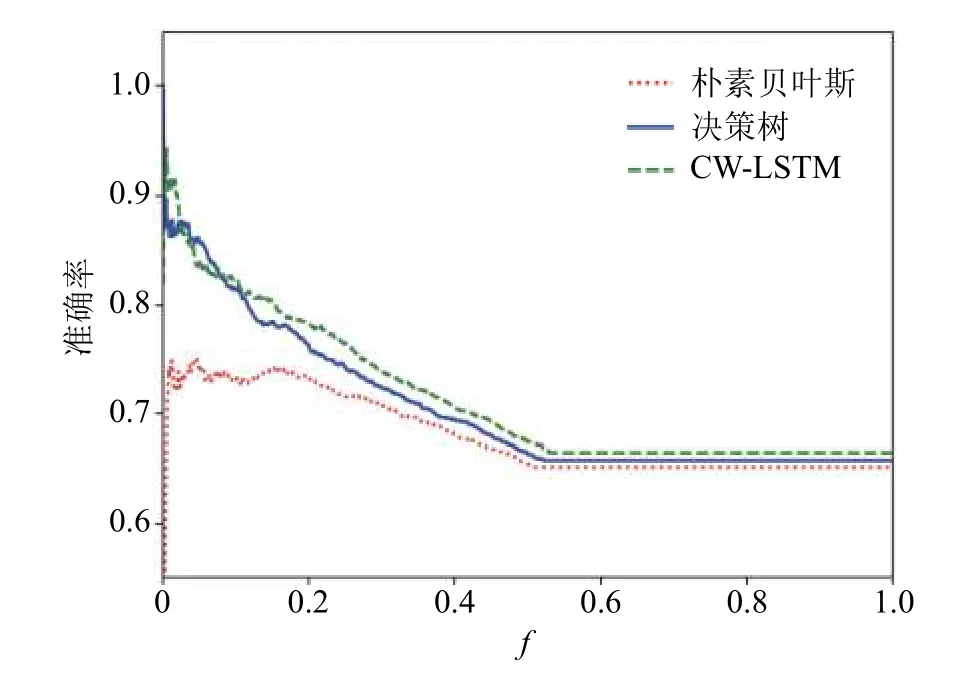
圖4 準確率隨結果集比例f 的變化

另外，通過決策樹模型，本文對特征的重要性進行分析，如圖5 所示。從結果可以看出，與消費有關的數據在預測中有著至關重要的作用，靠前的特征都與消費有關，這主要是因為預測目標就是學生經濟水平。在消費數據中，食堂消費數據更加重要，其平均值、最大值和次數的重要性都要高于其他消費數據。另外，提出的抽象數據特征也有著非常重要的作用，消費行為的熵和朋友圈經濟水平兩者的重要性之和超過了30%。其他統計特征重要性要遠低于消費數據。

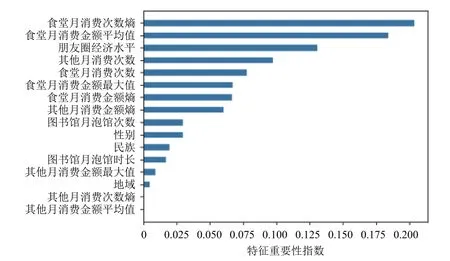
圖5 特征重要性指數

4 結 束 語

高校學生一直是國家和社會關注的焦點，本文利用大數據分析技術，對高校的家庭貧困學生進行挖掘。針對于高校學生的數據特點，抽取了學生的統計特征和行為時序性特征。然后根據學生數據的時序性特點，綜合CW-RNN 和LSTM 的優點，提出了CW-LSTM 算法來處理高校學生數據。最后利用某高校的真實學生數據，對模型進行了驗證。模型整體結果比樸素貝葉斯算法、決策樹回歸算法好。本文的研究方法可用于其他教育大數據分析，如畢業去向預測。本文的研究結果為實現高校更加精準扶貧工作提供了理論依據和確實可行的實驗方法，還可以在保證準確性的同時提高評審效率。