基于居民用戶畫像的綜合能源需求響應潛力量化模型

羅金滿， 溫兆聰， 董文杰， 李兆偉， 劉卓賢， 吳浩天

（1.廣東電網有限責任公司東莞供電局， 廣東 東莞 523000； 2.東方電子股份有限公司， 山東 煙臺 264000；3.華北電力大學， 北京 102206）

0 引言

綜合需求響應（Integrated Demand Response，IDR）是適應“新負荷”多元需求、提升電網柔性和彈性、增加綜合能源網絡靈活性的重要方式之一[1]～[5]。 綜合能源用能場景下，用戶畫像是洞察用戶需求、用能優化、能源交易、需求響應互動等精準服務的重要依據，通常包括用電特性特征、消費習慣特征等標簽[6]。 用戶響應潛力作為用戶畫像的重要標簽之一， 客觀地表征了用戶是否存在調控可能性、可調控容量、持續時間及響應速率，如何科學地計算響應潛力、更精確地描述用戶特性，成為綜合需求響應用戶畫像的重點課題之一。

文獻[7]從可消減的角度定義了居民需求響應的物理潛力。目前，需求響應潛力計算方法大致分為3 類：

①直接使用居民負荷特性表示響應潛力。 文獻[8]提出用最大負荷功率、平均負荷公里、最大負荷利用小時數、 用電量及電器構成表征用戶響應潛力。 文獻[9]提出采用用戶最大用電量、調用時間等因素表征用戶響應潛力；

②將用戶負荷特性采用特征映射的方式表示響應潛力。 文獻[10]利用多層神經感知網絡建立用電特征與調峰潛力之間的關系， 實現對居民調峰潛力的評價。 文獻[11]抽取行業典型用戶負荷作為樣本進行響應潛力評估；

③對居民負荷建模，進行響應潛力定量計算。文獻[12]針對居民負荷的可調節性、響應彈性等響應特性進行分類建模，綜合居民舒適度、滿意度進行響應潛力計算。 文獻[13]通過對居民部分家電建模，實現響應容量的定量計算。

綜上所述，現有文獻對于IDR 容量模型的研究仍然較少，且存在以下問題：一是上述文獻對居民負荷建模過程中沒有考慮到電器比例、 出行習慣等因素，不能精確模擬用戶用能行為；二是現有模型沒有考慮居民負荷的綜合用能行為， 忽略了居民可以使用天然氣進行替代用能的可能， 造成響應潛力計算不準確。

基于上述分析， 本文選取城鎮居民負荷為研究對象，詳細分析了居民用戶可調節負荷、可轉移負荷和可中斷負荷的動態運行特性， 構建居民負荷的綜合能源需求響應優化模型， 采用遺傳算法-序列二次規劃（GA-SQP）優化算法計算求解。

1 綜合能源場景下設備終端用能模型

按照參與需求影響的負荷性質， 綜合能源場景下的居民常用終端分為可調節負荷、 可轉移負荷和可中斷負荷3 類。其中：可調節負荷包括電動汽車（不考慮V2G）、綜合能源負荷（采暖、炊事）、熱水器等；可轉移負荷包括洗衣機、洗碗機等；可中斷負荷包括照明、娛樂性電器等。

1.1 可調節負荷

1.1.1 家用電動汽車充電模型（不考慮V2G）

在忽略充放電效率以及電池溫度變化等因素的情況下， 電池的容量、 充電前電池的荷電狀態（SOC）、 下段里程所需要的電池電量以及充電功率決定了電動汽車充電的持續時長[14]。

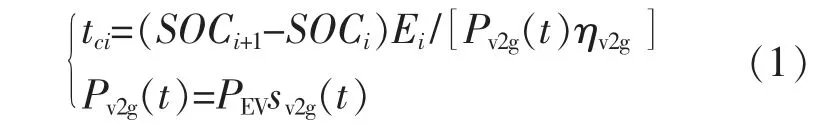
式中：SOCi，SOCi+1分別為充電前、后的荷電狀態；Ei為電池容量；ηv2g為充電效率；Pv2g（t）為電動汽車t 時刻充電功率；PEV為電動汽車額定功率；sv2g（t）為t 時刻充電指令，1 表示正在充電，0 表示未充電。

單臺電動汽車行駛后電池的SOC 由日行駛里程得出：

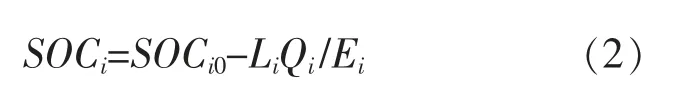
式中：SOCi0為電動汽車在啟動前的電池荷電狀態；Li為電動汽車出行的里程數；Qi為電動汽車每公里所消耗的電量，Qi=Ei/Lmax，其中Lmax為行駛里程的最大值。

1.1.2 空調用能模型

居民用戶的分體空調設備通常有兩類： 第一類為客餐廳使用空調，一般在非睡眠時段運行，其中包含了電力系統負荷的高峰時段； 第二類為臥室使用空調，一般在睡眠時段運行，為電力系統負荷的低谷時段[15]。 本文選取了第一類空調作為研究對象，控制時間為8：00-23：00。式（3）表示居民用戶空調在t 時刻的電功率Pac（t）和單位時間的制冷量Cac，t的關系，式（4）為電功率上下限的約束。

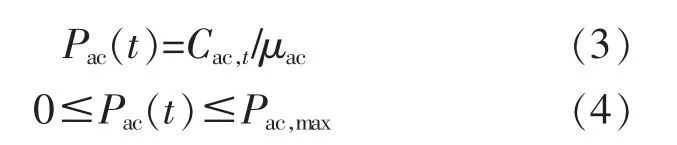
式中：μac為居民用戶空調的能效比；Pac，max為空調電功率的最大值。

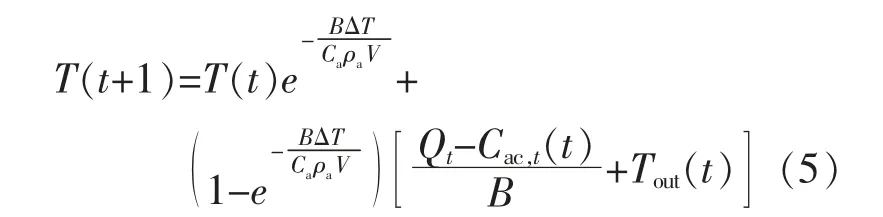
在居民用戶空調參與需求響應的過程中，通過控制室內的空氣溫度來控制空調的電功率。 通過能量守恒定律推導出離散形式的熱動態平衡方程，如式（5）所示，同時也是居民空調電負荷模型的約束條件。式中：T（t），Tout（t）分別為t 時刻的室內、室外溫度；B 為居民住宅的溫差傳熱系數；Qt為t 時刻建筑物瞬時得熱量（不包括溫差傳熱）；Ca為空氣定壓質量比熱容， 為1.005 kJ/（kg·K）；ρa為空氣密度；V 為客餐廳容積。

1.1.3 綜合能源負荷

1.1.3.1 燃氣掛爐用能模型

燃氣掛爐作為家庭供暖的一種裝置， 可以滿足居民用戶多居室的采暖需求。 其熱力學方程如下：

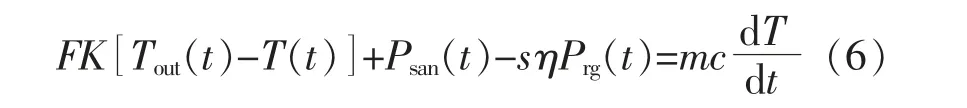
式中：F 為燃氣掛爐的導熱面積；K 為燃氣掛爐的導熱系數；Psan（t）為室內散熱功率；s 為狀態變量，1 表示運行狀態，0 表示待機狀態；η 為燃氣掛爐能效比；Prg（t）為t 時刻燃氣掛爐的制熱功率。

燃氣掛爐運行時工作時間與待機時間、 功率為

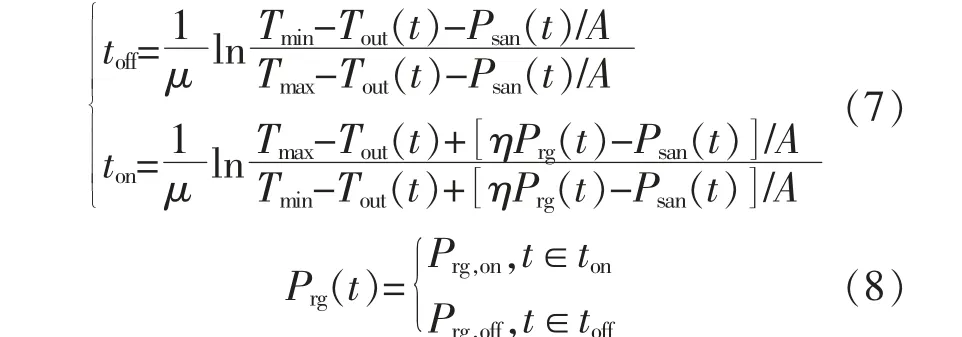
式中：Tmax，Tmin分別為燃氣掛爐工作溫度上、下限；μ 為常數，與導熱面積及導熱系數有關；A 為室內燃氣掛爐的系統導熱系數；Prg，on，Prg，off分別為運行功率、待機功率。

1.1.3.2 炊事能耗用能模型

炊事能耗分為燃氣能耗和電耗， 兩種能源耦合關系可描述為

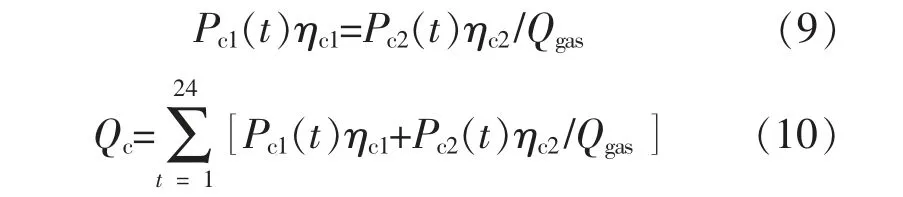
式中：Pc1（t），Pc2（t）分別為電能、燃氣炊事負荷；ηc1，ηc2分別為電能、 燃氣轉化為炊事能耗的轉化效率；Qgas為天然氣低熱值， 取9.97 kW·h/m3；Qc為1 d 內炊事負荷總量。

1.1.4 電熱水器用能模型

電熱水器有兩種工作狀態：①用水時段；②非用水時段[16]。狀態①時，熱水流失，溫度變化快，隨之帶走熱量； 儲水箱和室內空氣接觸也會消耗熱量。狀態②時，只有儲水箱和室內空氣接觸才會產生熱量消耗。根據能量守恒原理，電熱水器能量流入、流出守恒。 假定儲水箱中水溫恒定，電熱水器的模型為

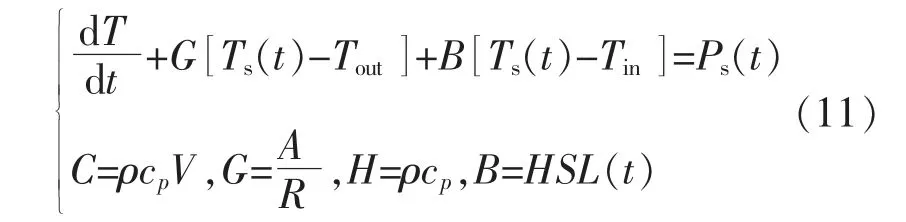
式中：SL（t）為居民用戶實時消耗水量[17]；Ts（t）為儲水箱中的實時水溫；Ps（t）為電熱水器的實時功率；V 為儲水箱體積；Tin為進水溫度；ρ 為水的密度；cp為水的比熱容；A 為電熱水器儲水箱表面積；R 為儲水箱熱阻。

運用歐拉法以及式（11），得到熱水器負荷跟隨時間變化的過程為

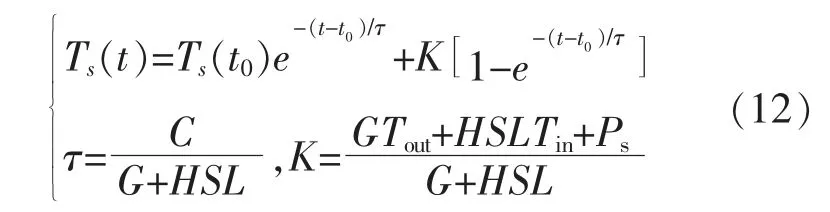
儲水箱內水溫在所設定的目標溫度上下浮動，最高溫度可達Thigh，最低溫度至Tlow，若熱水器改變工作狀態則須要滿足以下任一條件：①Ts（t）＞Thigh；②Ts（t）＜Tlow。 帶有遲滯環節的恒溫控制器可以通過式（13）來改變熱水器的工作狀態。

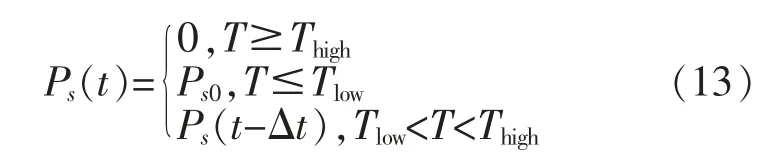
式中：Ps0為額定功率；Ps（t-Δt）為前一時刻功率。

1.2 可轉移負荷用能模型

在T 時間段中有M 個固定的工作周期，將每個工作周期中的工作模式固定而且不能中斷的用電設備（洗衣機、洗碗機等）定義為可轉移類電器。用戶對此類電器通常具有相對固定的習慣使用時間[18]，該類負荷用電特性模型如下：

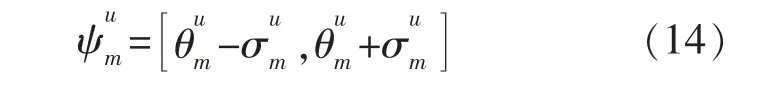
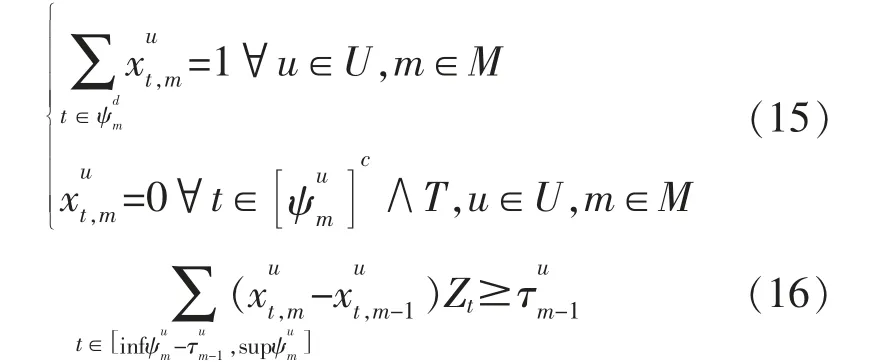
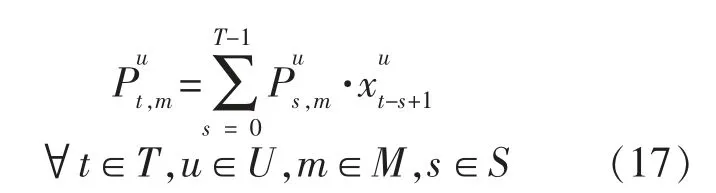
1.3 可中斷負荷

1.3.1 照明負荷用能模型

居民建筑照明具有需求量和需求面均較大的特點，是僅次于采暖空調的重要負荷[19]，[20]。建筑物照明能耗如下：

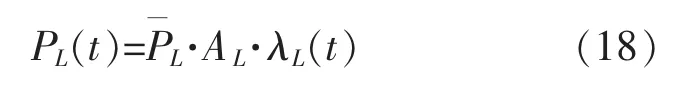
1.3.2 家用電器用能模型

家用電器主要包括電視、冰箱、空調、洗衣機等，其耗能可表述為

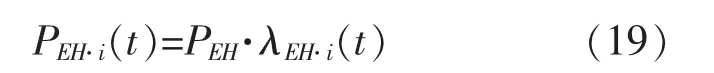
式中：PEH·i（t）為第i 個電器的運行功率；λEH·i（t）為不同電器在t 時刻正在使用的概率。

2 綜合能源需求響應潛力量化模型

2.1 目標函數

響應容量、 持續響應時間以及響應有效性共同決定了用戶響應潛力的大小。 本文基于居民用戶終端的動態運行特性， 選取各終端響應后功率為決策變量（各終端功率由其運行狀態決定），通過對響應值進行累加求和， 以累計響應容量Ppot最優為目標函數構建優化模型， 實現響應潛力量化。

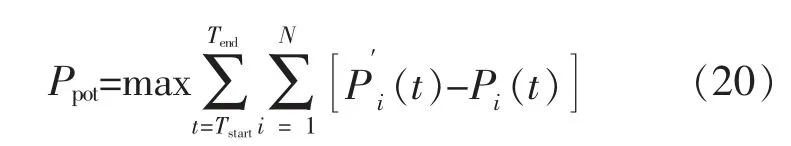
式中：Tstart和Tend分別為需求響應事件的開始和停止時間；N 為用戶用能終端總量；（t）為第i 個終端t 時刻的原始功率；Pi（t）為第i 個終端t 時刻響應后的功率。

2.2 約束條件

2.2.1 電功率平衡約束

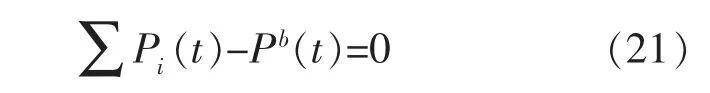
式中：Pb（t）為電網輸入電功率。

2.2.2 電動汽車充電約束

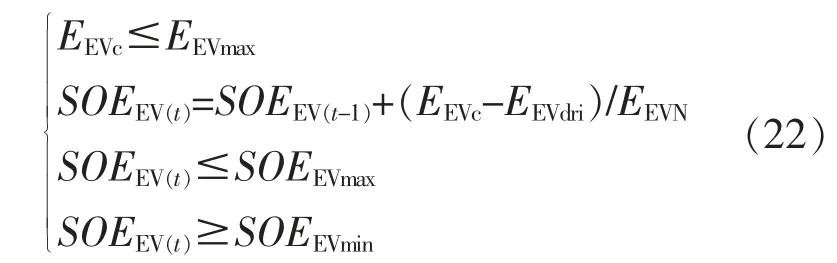
式中：EEVc為電動汽車充電消耗的電量；EEVmax為電動 汽 車 存 儲 的 最 大 電 量；SOEEV（t）為 電 動 汽 車 當前時段的剩余電能狀態；EEVN為電動汽車電池的總電量；EEVdri為電動汽車行駛所耗用的電量；SOEEVmax，SOEEVmin分別為電動汽車的最大、最小剩余電能狀態。

2.2.3 用能需求約束

室溫、水溫及照明約束為

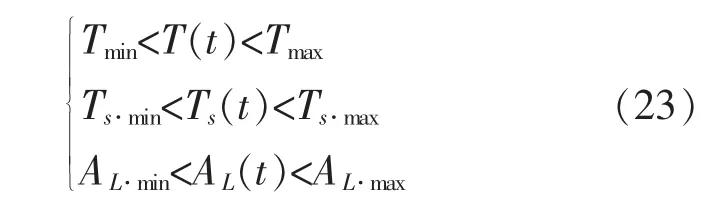
電器約束： 不同功能的家電會在不同的時間使用。根據使用時間不同，分為生活必備型和辦公娛樂型。 其中：前者使用時間比較固定，呈現規律性；后者使用時間不固定，因人而異。

運行約束：

①空調運行最小時間限制和燃氣掛爐運行最小時間限制為

②其余電器運行時間小于24 h。

2.2.4 設備功率約束

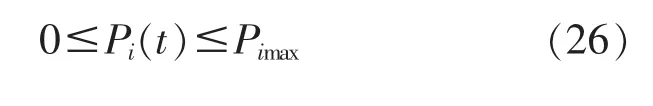
2.2.5 需求響應有效性約束

根據某省份需求響應政策中對用戶響應有效性判定的有關要求， 建立居民負荷響應有效性約束， 以居民用戶未參與需求側響應的用電負荷為基線負荷， 用戶參與需求側響應有效性約束條件如下。

①響應時段內，最大負荷不高于基線負荷

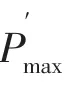
②響應時段內，平均負荷低于基線平均負荷

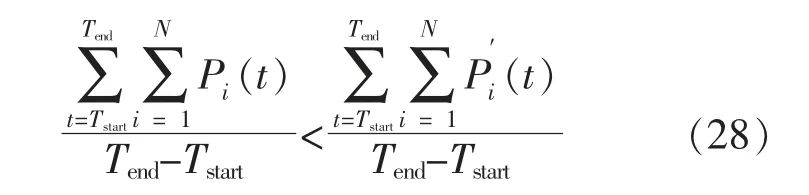
3 算法

本文提出的優化模型以各用電終端參與響應的功率為原始自變量， 而各用電終端的功率與設備運行狀態對應。 一部分終端分為運行和待機兩種狀態，分別對應不同的功率值，為0-1 變量；另一部分終端的功率受環境或其他因素影響， 為連續變量。 因此， 該模型實際上為混合整數優化模型， 可根據各類用電器模型， 分類使用遺傳算法（Genetic Algorithms，GA） 和序列二次規劃算法（Sequential Quadratic Programming， SQP） 進行求解。

GA 擁有內在的隱含并行性和自適應的調節搜索空間， 求解速度快， 并且可保證全局最優。SQP 對于非線性約束最優化問題是一個非常有效的算法， 將原始問題劃分為一系列二次規劃的子問題進行求解。

在本文模型涉及的變量中，電炊事、家用電器的使用狀態為整數序列， 氣炊事與電炊事約束條件相關聯， 因此將氣炊事變量變換為0-1 變量，三者共同使用GA 計算最優值。 變異概率取值為0.6，種群大小為10。

GA 流程如下：

①設定算法的各類控制參數；

②編碼生成初始種群，計算適應度值；

③選擇交叉變異操作，生成新種群，與已有整數解進行適應度比較；

④判斷終止條件是否滿足， 選擇退出程序或輸出最優解。

空調、壁掛爐、洗衣機、照明、熱水器等用能終端均可變換為受某自變量影響的因變量，使用SQP 求得最優值。 其中：空調、壁掛爐能耗可變換為自變量為室溫T 的函數， 模型計算中的其他相關量，如建筑物瞬時熱當量、人體代謝率等物理量，按采樣時段內的平均值計算；電動汽車充電能耗可變換為自變量為Li的函數；洗衣機能耗可變換為自變量為時間t 的函數； 照明可變換為與λL（t）相關的函數，其中AL在每個采樣時刻為固定值；熱水器能耗可變換為自變量與SL（t）相關的函數。 以上自變量可構造初始矩陣，根據設定目標函數和約束， 使用SQP 求得最優自變量矩陣。

SQP 流程如下：

①設定參數條件，如連續變量、整數變量、迭代次數等；

②輸入目標函數，根據要求設定約束；

③使用SQP 求解混合整數規劃問題；

④存儲求解結果；

⑤判斷是否滿足最優條件，滿足退出計算，不滿足轉到步驟③。

由以上過程可進一步推得功率值， 得到每個時段的最優功率。

混合算法流程示意圖如圖1 所示。

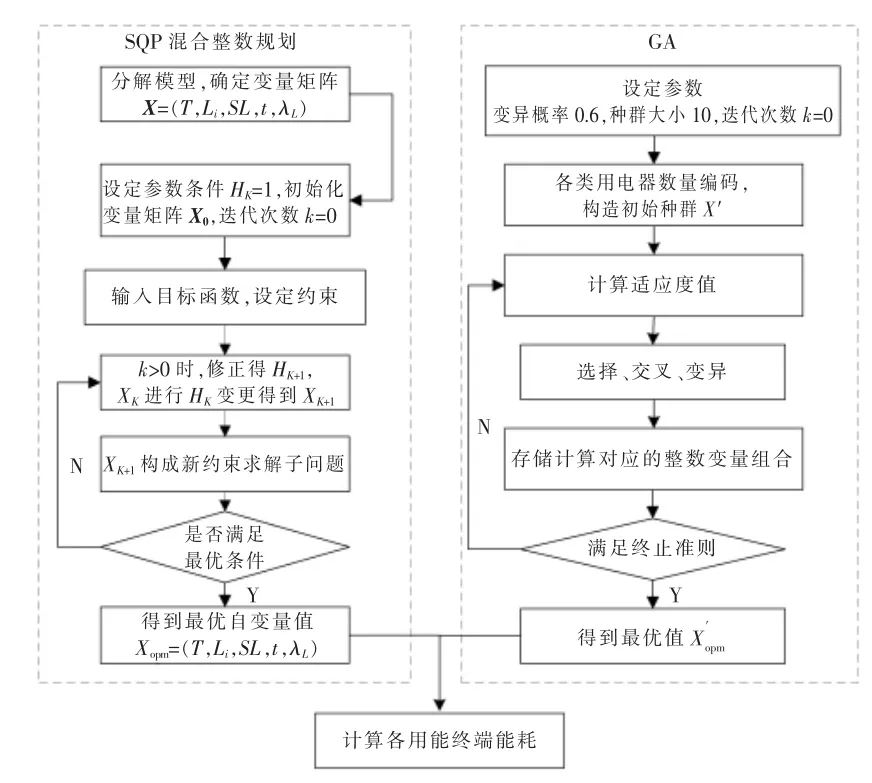
圖1 混合算法流程示意圖Fig.1 Schematic diagram of the hybrid algorithm flow

4 算例分析

4.1 模型驗證

算例選取華南地區某小區居民夏冬季典型日用能數據，數據間隔為1 h。 華南地區夏季氣候炎熱，居民午間炊事、休息時段和晚間居家時段為供電高峰時段，削峰響應需求較為突出。選用的居民常用終端包括空調、壁掛爐、電動汽車、電炊事、氣炊事、洗衣機、照明、熱水器及其他家電，相應的負荷模型參數如表1 所示。

表1 用戶用電器參數Table 1 Electrical parameters of users

為驗證本文所提模型的有效性，分別采用傳統計算模型和本文提出的需求側響應潛力計算模型，對比分析3 種場景下用戶的響應情況。

場景一：不同家用電器比例對響應量的影響。本文選取傳統潛力計算模型中的最大負荷功率、平均負荷率、 最大負荷利用小時數3 個指標數值相同的用戶， 分析不同家用電器比例對用戶響應量的影響。

基礎用戶：選取老年居家族為基礎用戶，使用電器種類和比例為表2 中A 類用戶。

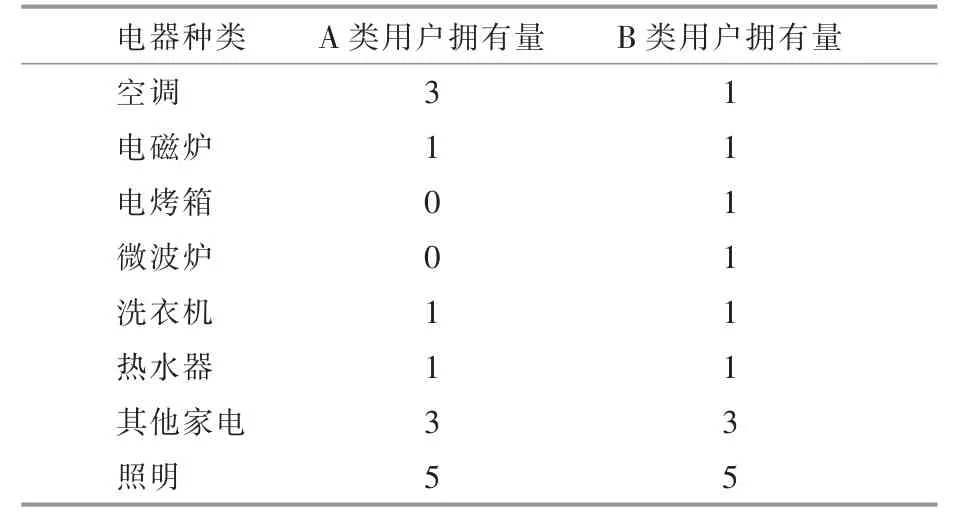
表2 用戶設備及功率匯總表Table 2 Summary of user equipment and its power

對照用戶1： 選取炊事為主的用戶作為對照用戶1，使用電器種類和比例為表2 中B 類用戶。兩類用戶的優化時間均選取8：00-22：00。

場景二：不同出行習慣對響應量的影響。本文選取最大負荷功率、平均負荷率、最大負荷利用小時數相同的用戶， 分析不同出行習慣對用戶響應量的影響。

對照用戶2：根據用戶出行習慣不同，選取工作日上班族用戶作為對照用戶2。 其設備比例與基礎用戶完全相同，用電時間為每日7：00-9：00，18：00-24：00，午間不涉及炊事能耗。

圖2～4 分別為基礎用戶、對照用戶1 及對照用戶2 參與IDR 前后的負荷曲線。

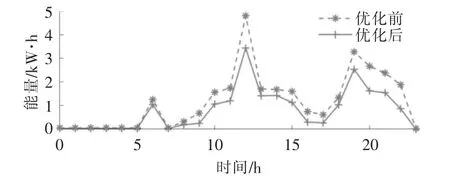
圖2 基礎用戶優化前后耗能曲線Fig.2 Energy consumption curve of basic users before and after optimization

圖3 對照用戶1 優化前后耗能曲線Fig.3 Energy consumption curve of contrast user 1 before and after optimization

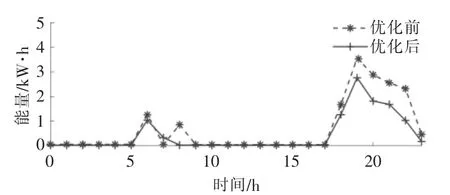
圖4 對照用戶2 優化前后耗能曲線Fig.4 Energy consumption curve of contrast user 2 before and after optimization

由圖2～4 可知：基礎用戶參與IDR 后響應量為9.12 kW·h，占優化前耗能的31.7%；對照用戶1 參與IDR 后響應量為6.62 kW·h， 占優化前耗能的27.3%；對照用戶2 耗能曲線在晚間上升，參與IDR 后響應量為5.76 kW·h， 占優化前耗能的29.48%。 當最大負荷功率、平均負荷率、最大負荷利用小時數等負荷特性相同時，用戶出行規律、用戶電器比例等都會影響用戶響應潛力。因此，本文提出的綜合能源需求響應潛力量化模型能夠更加客觀地體現用戶響應潛力。

場景三：不同負荷類型對響應量的影響。本文提出的綜合能源負荷需求側響應模型包含了熱負荷參與響應的情況， 為了與常規電負荷響應模型進行對比分析， 分別選取基礎用戶夏季及冬季典型日的耗能數據進行響應量計算, 結果分別如圖5，6 所示。

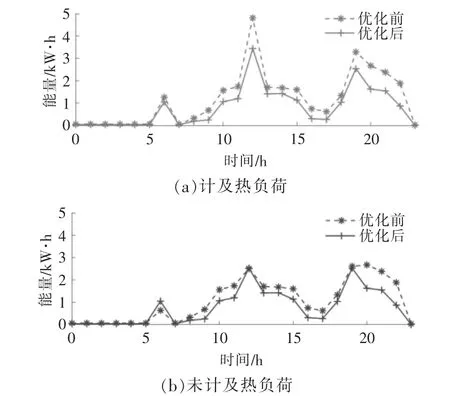
圖5 基礎用戶夏季負荷優化前后曲線Fig.5 Energy consumption curve of basic users before and after optimization in summer

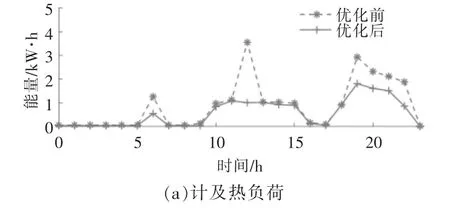
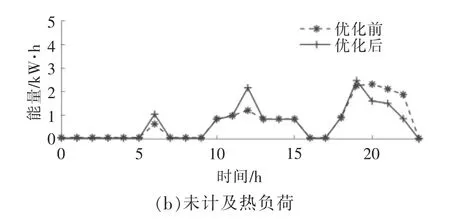
圖6 基礎用戶冬季負荷優化前后曲線Fig.6 Energy consumption curve of basic users before and after optimization in winter

由圖5，6 可知： 該用戶未計及熱負荷參與響應時，夏季的響應潛力為6.44 kW·h，計及熱負荷后的響應值增加了6.7%，達到9.12 kW·h；冬季的響應潛力為7.48 kW·h，占優化前耗能的35%。 與夏季負荷相比，冬季熱負荷中增加了燃氣掛爐，因此冬季的響應潛力明顯增加。可見，通過鼓勵用戶進行能源間的響應行為，可增加居民響應潛力，并且冬季有壁掛爐的用戶中尤為明顯。

4.2 響應量潛力分析

由于用戶耗能的主要因素，如空調、熱水器、電炊事、氣炊事、照明等家電耗能受每戶人數的影響，因此，根據每日人均空調負荷、人均熱水負荷、人均炊事負荷及家電使用概率， 由各種設備終端用能模型計算每日用戶人數變化的耗能數據。 進而通過本文模型計算相應的響應潛力， 結果如圖7，8 所示。

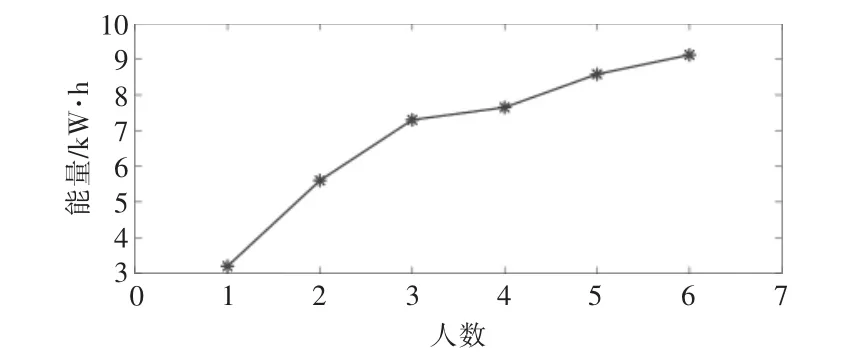
圖7 家庭人數與響應潛力變化關系Fig.7 Relationship between household population and response potential

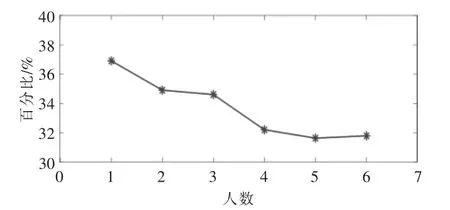
圖8 家庭人數與響應潛力比重變化關系Fig.8 Proportion change diagram between household population and response potential

由圖7，8 可知，隨著家庭人數的增長，響應潛力隨之增加， 但響應潛力在用戶總負荷中的比重下降。這是因為家庭人數增長后，一方面增加了家庭總能耗， 為參加IDR 提供了更大的響應空間；另一方面降低了負荷優化的靈活性， 如在晚高峰時段，4 個人依次使用熱水器和一個人使用熱水器對于熱水器的優化靈活性大大降低， 但同時增大了可響應的電量。

5 結論

本文選取城鎮居民負荷為研究對象， 根據可調節負荷、 可轉移負荷和可中斷負荷的動態運行特性，構建了居民用戶常見負荷的用能模型；在此基礎上，建立綜合能源需求響應優化模型，實現了響應潛力的定量計算。通過算例分析，得到以下結論。

①本文基于居民用戶畫像的綜合能源需求響應潛力量化模型可以客觀地評價用戶可參與響應的最大潛力。

②在用戶負荷特性相似的情況下， 用戶的用電設備比例、出行習慣等均會影響用戶響應潛力，響應潛力變化可達優化前能耗的25%以上。

③通過鼓勵用戶進行能源間的響應行為，可增加居民響應潛力， 并且在冬季有壁掛爐的用戶中尤為明顯，響應潛力可達優化前能耗的35%。

④隨著家庭人數的增長，響應潛力隨之增加，但響應潛力在用戶總負荷中的比重下降。