強衰減介質中地震波場的頻率—空間域特征

張 壹 王 赟* 陳本池 王祥春

（①中國地質大學（北京）地球物理與信息技術學院，北京100083；②中國石油化工股份有限公司科技部油田處，北京100728）

0 引言

實際地球介質復雜多樣，傳統的完全彈性介質理論受到嚴峻的挑戰，越來越需要基于黏彈性介質理論研究實際介質中地震波的傳播特征和衰減規律［1-2］。前人的研究表明，即使完成球面擴散和界面因素造成的衰減補償之后，地震波在深層介質中傳播的能量仍因介質的黏滯損耗遠弱于淺層介質中的波場能量［3］。中國西部黃土塬區、沙漠覆蓋區油氣資源豐富，近地表介質疏松多孔、彈性差，地震波表現為強衰減、高頻散、低分辨率等特征［4-5］；若進一步考慮淺表介質孔隙、裂隙發育，孔隙空間中的流體多表現黏滯性時就需要考慮介質的強吸收衰減性。

對于地震波在實際介質傳播中的衰減特征，目前最主要的研究理論包括黏彈性介質理論和孔隙雙相介質理論［6］。黏彈性介質理論的發展始于Stokes方程的建立［7］，之后基于彈性滯后和質點內摩擦等衰減機制，構建出多種符合實際的黏彈性介質模型［8］。例如線性流變模型、達朗貝爾模型以及常Q介質模型等都是在本構方程或運動方程中引入一定的非彈性衰減機理，進而使人們對黏滯波場特征和地震波非彈性衰減有更真實的認識［9-12］。描述孔隙介質雙相性的重要理論包括宏觀Biot理論［13］、微觀噴射流理論［14］和BISQ 理論［15］，前兩種理論分別是根據流體的宏觀流動和微觀噴射，研究介質的孔隙結構和流體效應對地震波傳播衰減的影響，而最后一種理論是它們的有機統一。

杜啟振等［16］發現，在地震頻率范圍內，地震波的衰減和頻散特征的準確描述不能只考慮黏彈性介質理論和孔隙雙相介質理論中的一種，還需要應用黏彈性模型刻畫巖石骨架的性質。隨后，Nie 等［17］和凌云等［18］分別將Kelvin-Voigt體和標準Zener體的本構關系引入到BISQ 模型中，建立了黏彈孔隙介質模型，研究地震波在黏彈孔隙介質中的衰減規律。強衰減模型是謝佩瑜等［19］在達朗貝爾模型的基礎上，通過引入與孔隙度和滲透率等參數相關的黏滯項，并利用黏彈性拉梅系數替換彈性拉梅系數的方式建立的一種衰減介質模型。雖然強衰減模型是以運動方程描述介質的黏滯衰減特征，但是它能全面地考慮孔隙度、流體黏度和介質黏彈性等因素對地震波衰減和頻散的影響。謝佩瑜等［19］還根據實際地震數據，驗證了強衰減模型相比于帶耗散的彈性Biot模型、BISQ 模型以及黏彈性BISQ 模型能更精確表征近地表介質衰減特征。

考慮到強衰減模型波動方程中的黏彈性拉梅系數是與頻率相關的復數型參數，時間域數值算法顯然不能用于強衰減模型的正演模擬。而且實際地震波是由多個單頻簡諧波組成的復合波，即地震波的傳播與頻率相關，不同頻率成分具有不同的波場特征。若要實現強衰減模型介質的正演模擬，分析全頻帶范圍內地震波的傳播特征，需要采用頻率—空間域數值算法。

頻率—空間域數值模擬最先由Lysmer等［20］提出，之后相繼出現5點、9點和25點有限差分算法。各種頻率域正演方法都是對每一頻率下所有空間網格整體求方程組，其計算誤差分配到各網格點上，而且各單頻切片的計算互相獨立，因此能實現數值的并行計算，并不存在累計誤差。隨著加權平均思想和高精度模擬的深入研究，Min等［21］提出了優化的25點頻率—空間域有限差分算法，與其他方法相比，該算法精度高、適用范圍廣，即只要滿足每個橫波波長達3.3個網格就能保證數值誤差低于1%。有學者采用優化的25點有限差分法實現了黏彈各向異性介質和孔隙雙相介質等的波場模擬，取得了不錯的效果［22-25］。

在前人研究的基礎上，本文將優化的25點有限差分法應用到強衰減模型波動方程的數值計算，研究強衰減模型介質中地震波的傳播特征，以及孔隙度、流體黏度和介質黏彈性等因素的衰減機制。

1 強衰減介質模型

1.1 波動方程

強衰減模型是一種綜合性的黏彈性介質模型，不僅包括介質中流體流動引起的耗散，還包括介質自身的黏彈性所引起的耗散，其波動方程為

λ*、μ*是與頻率相關的黏彈性拉梅系數，其具體表達式為

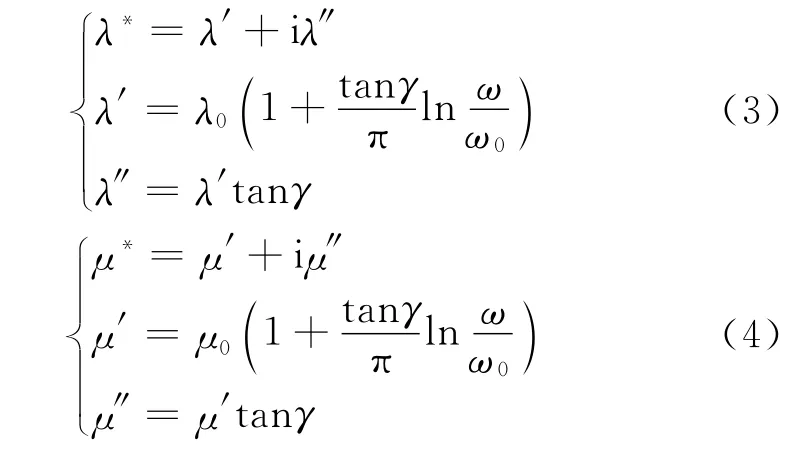
式中：λ0、μ0 是彈性拉梅系數；ω0是基準圓頻率；tanγ是介質的黏彈性參數，Yang 等［26］給出了隨頻率線性變化的一般表達式

其中：tanγ1、tanγ2是最低圓頻率ω1和最高圓頻率ω2對應的黏彈性參數。

1.2 地震波的衰減函數和頻散函數

振幅函數和相位函數是波動方程通解中的重要組成，可通過復波數確定，并能用于介質品質因子和等相位面速度的定義。為了研究強衰減模型介質中地震波的衰減和頻散特征，謝佩瑜等［19］對波動方程（式（1））做縱、橫波分離和傅里葉變換，分別得到縱波和橫波的頻散方程。由頻散方程求解地震波的復波數，并根據Dvorkin等［15］的逆品質因子和相速度的計算公式，得出強衰減模型的逆品質因子和相速度

2 優化的頻率——空間域25點有限差分算法

二維情況下，式（1）在頻率—空間域可表示為

式中：u、v分別為x 和z 方向的位移分量；sx（ω）、sz（ω）分別為x 和z 方向的頻率域震源函數。

2.1 頻率—空間域25點優化差分算子

式中：（i，j）為網格中心點坐標；Am、Bn（m＝1、2、…、6，n＝1、2、3）以及C、D、E、F 是頻率—空間域25點優化差分算子的加權系數；Δx、Δz為空間網格步長。同理也可定義垂直分量v的差分算子。

對于上述差分算子加權系數，需要構造目標函數，使離散模型和連續模型的相速度相等，這是一個非線性優化問題，可利用Gauss-Newton法求解［27］。加權系數的具體取值參考Min等［21］的研究結果，該組優化的加權系數考慮到各種傳播角度和所有泊松比情況，能適用各種模型的正演模擬，可以在α＝vS／（f0Δx）≥3.3（其中f0為震源主頻）的條件下保證數值算法的高精度［28］。

為了探討優化的25 點差分算法的穩定性，在vS＝604m／s、f0＝25Hz的情況下，分別設置Δx＝8、2m（對應α＝3.02＜3.3和α＝12.08＞3.3）兩種不同數值條件，下文將這兩種數值條件依次稱為第一數值條件和第二數值條件。在第一數值條件下，適當修改25 點優化差分加權系數中的一些數值，如令B1＝0.508781、B2＝0.170898、B3＝－0.015727、C＝0.6596838、D＝0.211686，使離散模型與連續模型的相速度不同，對比、分析優化的25點差分法在壓制數值各向異性上的有效性。由第一數值條件和第二數值條件正演出的波場快照如圖2a、圖2b所示。對比圖2a與圖2b可見，當數值算法未能滿足相應的穩定性條件時，波場快照上會表現出明顯的數值頻散和各向異性現象，所以波場模擬應首先考慮數值算法的穩定性條件。

2.2 構造最佳匹配層吸收邊界條件下的差分方程

在正演模擬中，由于計算區域有限會不可避免地引入人為反射界面，嚴重影響最終模擬的效果，有必要構造邊界條件壓制邊界反射［29］。常用的PML邊界條件，吸收效果較好［30］，其基本思想是在計算區域四周設置一定厚度的完全匹配層吸收衰減邊界反射波的能量［31］。

圖2 不同數值條件下的波場快照

若將PML邊界應用于彈性波頻率—空間域的正演模擬，需要將波動方程轉換到復坐標系下。復坐標系變換可表示為

式中：～xj是復坐標系變量，其中j＝1、2分別表征x、z兩個方向；xj是常規坐標變量；匹配層吸收因子ej＝1＋σj／（iω），其中σj＝2πa0f0lj／L 是衰減系數，在非PML層內取值為零，a0為常數，lj是計算區域到PML層交界處的距離，L 是PML層的厚度。當復坐標變量替換常坐標變量之后，二維波動方程（式（7））中的空間偏導項將變為

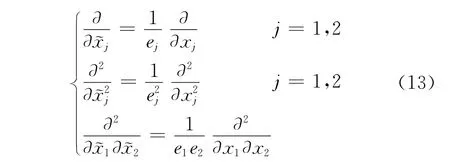
對比圖3中計算區域有、無PML邊界的彈性波單頻切片可見，當計算網格中不含PML層時，單頻切片中的波場信息混亂，即全頻段所有單頻切片經反傅里葉變換之后，不能得到正確的時間域波場值；當計算邊界含有一定厚度的PML層時，單頻波場中的波前面自震源處向外傳播，呈同心圓狀，不受任何邊界反射的影響。

圖3 無（a）、有（b）PML邊界單頻切片對比

將式（8）～式（11）的差分格式代入式（7）中，應用式（13）能構造出含PML邊界的頻率—空間域彈性波離散化波動方程（以水平向為例）

式中：系數p1～p9以及q1、q2是構造式（14）時合并所有同類項而得的系數。當所有網格點的波場值都按式（14）求解時，可建立線性方程組

式中：P 為N 階系數阻抗矩陣，對于二維情況下N＝2Nx×Nz，Nx、Nz分別是x、z 方向上的網格點數；U、S均為N 維列向量，對應元素分別是各網格點頻率—空間域波場值和震源函數值。頻率—空間域波場模擬實則是大型線性方程組的求解過程［32］，因此，本文在25點優化差分的基礎上結合9點差分處理局部邊界網格點，并采用LU 分解法求解大型稀疏矩陣方程，計算出各網格點全頻帶范圍內的波場值。一旦求出全頻帶波場值，就能通過反Fourier變換得到整個計算網格的時域波場值。

3 強衰減模型數值模擬

3.1 震源加載

不同于時間域方法中直接在網格點的速度分量或應力分量上增加地震子波函數，頻率—空間域波場模擬的震源加載需要構造與頻率相關的震源矩陣。殷文等［33］總結幾類頻率域震源加載機制，并給出縱、橫波震源在網格點上的加載公式，即

式中：s（ω）為頻率域震源子波函數；Kx和Kz是震源的方向系數。本文利用四點網格模擬縱波源和橫波源，若將網格左、右上角分別定義為0、1，左、右下角定義為2、3，縱、橫波源的方向系數分別為

3.2 均勻各向同性介質波場模擬

為了驗證優化的25點差分法在強衰減模型波場模擬中的有效性，本文首先設計一個符合近地表介質特征的均勻各向同性介質模型，網格數為100×100，PML層厚為50m，網格間距Δx＝Δz＝2m，其物性參數（表1）的選擇參考了Cui等［34］在勝利油田采集的微測井數據。根據這組實測數據計算的黏彈性參數為

正演時間采樣間隔Δt＝1ms，采樣點數為1024。為了對比波場信息，在模型中心分別加載縱波源和橫波源。震源子波是主頻為25Hz的Ricker子波。

圖4、圖5分別為縱、橫波源單頻波場切片，波前面呈同心圓狀，不同頻率的地震波因為波長不同使單頻切片上的“同心圓”間距不同，而且在相同頻率的情況下，橫波單頻切片上的“同心圓”比縱波“同心圓”分布更為密集。與完全彈性介質相比（圖4b、圖4d、圖5b、圖5d），強衰減介質單頻波場（圖4a、圖4c、圖5a、圖5c）的波前面能量比較弱，同心圓軌跡較模糊，表明地震波各頻率成分受到嚴重的衰減，傳播距離越遠越嚴重。圖6為兩種源激發的60ms波場快照，波前面也是以震源位置為中心的正圓形，其波前面與理論相符。

表1 均勻各向同性介質模型物性參數

圖4 縱波源強衰減與完全彈性介質不同頻率的單頻波場切片對比

圖5 橫波源強衰減與完全彈性介質不同頻率的單頻波場切片對比

圖6 強衰減介質模型60ms的波場快照

圖4、圖5單頻切片及圖6的波場快照充分地描述了地震波在均勻各向同性、強衰減介質中的傳播特征，表明優化的25點差分法模擬強衰減模型中地震波場的可行性。

強衰減模型全面地考慮了介質自身的黏彈性、孔隙度和黏性流體的流動作用，對近地表地震波衰減規律的預測和復雜黏彈性介質的描述更接近于實際［19］。在表1所示物性參數的基礎上，綜合近地表介質孔隙結構、干燥疏松程度、黏滯性等適當地選擇不同的物理參數，分析孔隙度、流體黏度和介質黏彈性對介質衰減特征的影響。當震源位于（90m，15m）處激發，在地表以3m 的道間距設置一條排列接收，將縱、橫波源模擬記錄合并在一起，結果如圖7所示。圖7中的地震記錄能清楚地顯示縱波和橫波在均勻半空間強衰減介質中的波場傳播信息。

圖8～圖16展示了不同孔隙度、不同流體黏度和不同介質黏彈性條件下的x＝120m 處的單道地震記錄及其振幅譜和地震波速度頻散曲線。由圖8、圖11和圖14可清楚看出，隨著介質孔隙度和流體黏度的增大以及介質自身黏滯性的增強，地震波的振幅值越來越小，即介質的任何一種物性條件變差時，介質對地震波的吸收衰減能力變強。在近地表介質條件下，孔隙度的變化所引起的地震波衰減幅度大于另外兩種因素，說明近地表介質的疏松結構是造成介質強衰減性的關鍵。

圖7 均勻強衰減介質地震記錄

圖8 不同孔隙度條件下縱（a）、橫波（b）單道記錄對比

圖9 不同孔隙度條件下縱（a）、橫波（b）單道振幅譜對比

圖9、圖12和圖15分別為圖8、圖11和圖14單道地震記錄對應的振幅譜，可見隨著介質物性條件的變差，各頻率成分的能量越來越弱，這就解釋了圖4和圖5中強衰減單頻切片相對于彈性單頻切片較模糊的原因。而且還可以看出：①隨介質自身黏滯性的增強，高頻地震波能量衰減強于低頻地震波，振幅譜呈現主頻降低的現象；②介質孔隙度和流體黏度的增大能使整個地震頻率范圍內的波場能量發生衰減，其中有效頻帶內的能量衰減最強，但未出現主頻降低的現象。

能量衰減和速度頻散都是黏彈性介質地震波場重要特征，本文基于強衰減模型的相速度公式（式（5）），計算各條件下地震波的速度頻散曲線如圖10、圖13 和圖16 所示。可以看出，介質孔隙度和流體黏度的增大以及介質黏彈性的增強，都能使地震波速度的頻散特征表現更為明顯，其中高頻頻散弱于低頻頻散。

圖10 不同孔隙度條件下縱（a）、橫波（b）頻散曲線對比

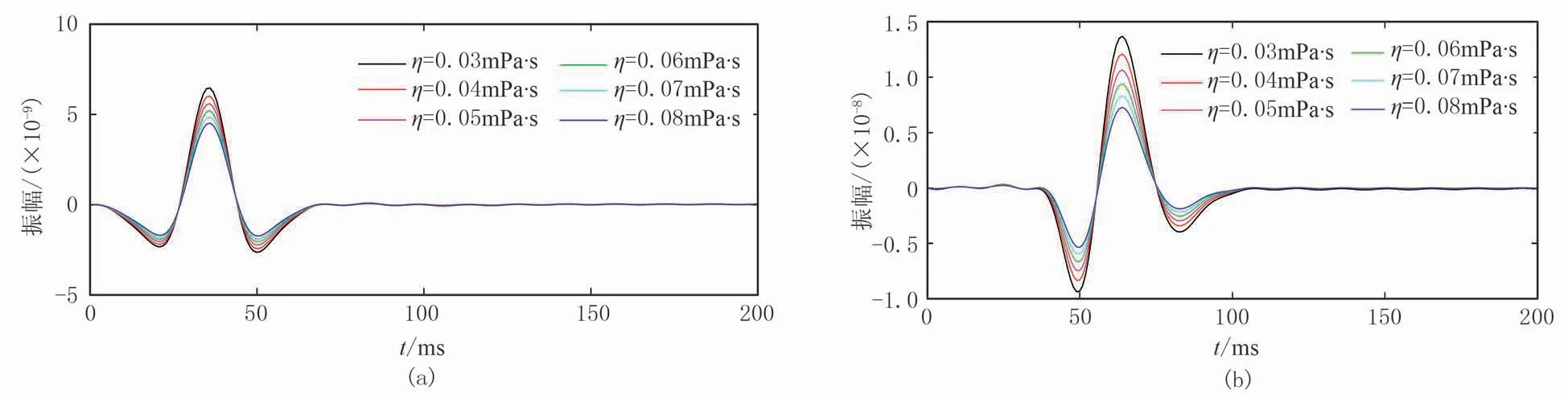
圖11 不同流體黏度條件下縱（a）、橫波（b）單道記錄對比

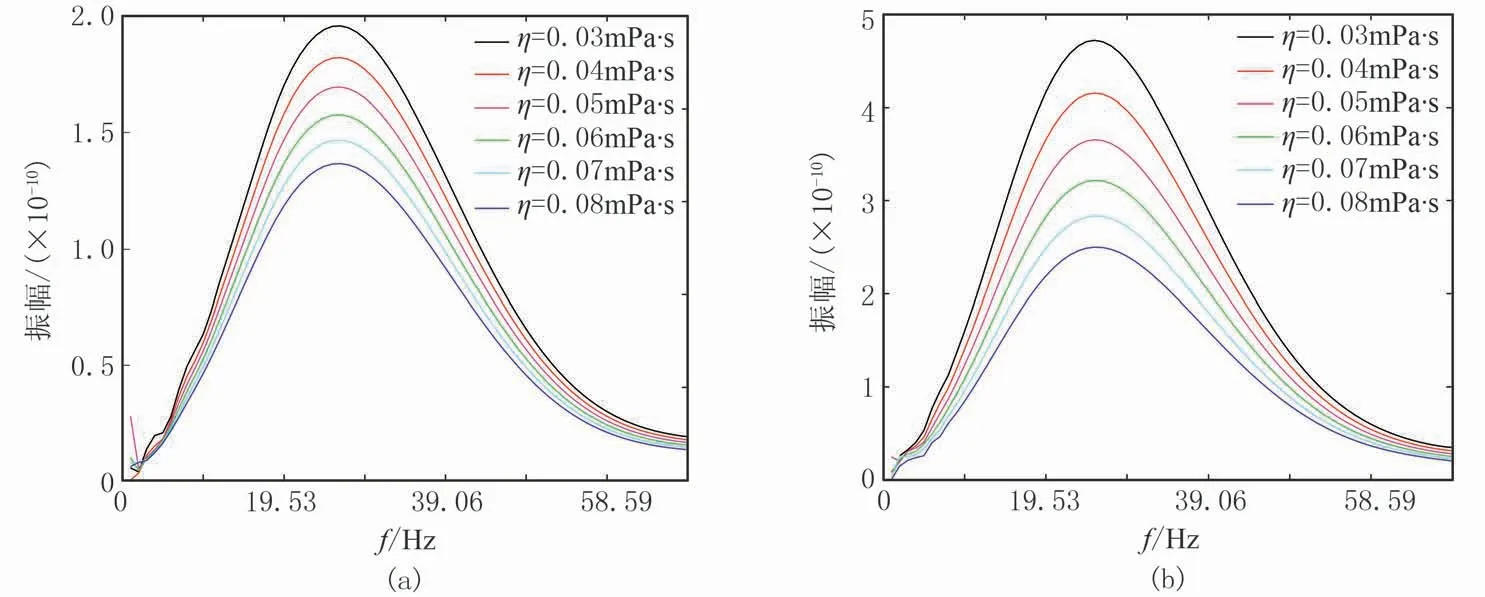
圖12 不同流體黏度條件下縱（a）、橫波（b）單道振幅譜

圖13 不同流體黏度條件下縱（a）、橫波（b）頻散曲線

圖14 不同介質黏彈性條件下縱（a）、橫波（b）單道記錄對比

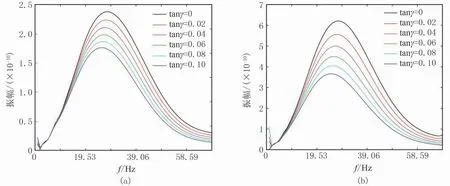
圖15 不同介質黏彈性條件下縱（a）、橫波（b）單道振幅譜對比

圖16 不同介質黏彈性條件下縱（a）、橫波（b）頻散曲線對比

綜合對比圖8～圖16 可以發現，介質的孔隙度、流體黏度以及介質黏彈性對縱波和橫波傳播衰減的影響不同，隨著這三個參數的逐漸增大，橫波振幅的遞減幅度大于縱波。出現這種現象的原因為：

（1）近地表介質結構疏松、多孔，當介質的孔隙度增大時，介質的抗剪切能力會變得越來越弱，導致橫波的衰減隨孔隙度的增大而變強。

（2）強衰減模型波動方程（式（2））中的耗散系數與孔隙度、滲透率和流體黏度相關，其中流體黏度反應流體與固體骨架之間的黏滯作用，這種相互作用是導致地震波衰減的重要因素［35］。橫波不能在流體中傳播，在橫波傳播過程中流體相對于固體骨架的運動位移大于縱波，因此隨流體黏度的逐漸增大，橫波能量的遞減幅度明顯大于縱波。

（3）近地表介質由于長期受風化、剝蝕等外力作用使固體骨架表現出明顯的黏彈性，作為骨架波的橫波受到的影響比較明顯。

綜上所述，強衰減模型考慮多種物理因素，以運動方程刻畫介質的衰減規律是合理、有效的，而且它預測的縱、橫波衰減機制與實際相符，值得在油氣富集區推廣應用。

3.3 含低速層的兩層介質波場模擬

為了研究近地表低速層介質對深層波場信息的影響機制，本文設計一個物性參數如表2所示的兩層介質模型：模型尺寸為175m×175m，其中上層是厚70m 且疏松多孔的黏彈性介質，下層是致密彈性介質，選擇主頻為25Hz的Ricker子波作為縱波源在（87.5m，35.0m）處 激 發，50 個 檢 波 器 點 以3.5m的間隔均勻分布在地表。

圖17展示了兩層介質模型的近地表低速層分別由強衰減模型、一般黏彈性模型（達朗貝爾模型）和完全彈性介質理模型模擬的地震記錄，圖中可見直達波、反射縱波、轉換橫波。若近地表介質由完全彈性或由一般黏彈性模型描述時，各地震分量中攜帶深層介質信息的反射波和轉換波能量較強、記錄直觀清楚，而且兩種條件下的地震記錄差異較小。但在基于強衰減模型所模擬的地震記錄上，反射波和轉換波的同相軸較模糊、能量弱。黃土塬、沙漠等地一般都會因表層覆蓋較厚的低速層介質，對地震波的激發和接收產生巨大的影響［36］。

表2 兩層介質模型物性參數

圖17 強衰減（左）、黏彈性（中）及完全彈性機制（右）下兩層模型地震記錄

為了更直觀地對比完全彈性、一般黏彈性和強衰減機制下的波場信息，抽取圖17地震記錄中x＝140m 處水平分量單道信號，并計算其振幅譜（圖18）。由圖可見：黏彈性介質較彈性介質對地震波高頻成分有明顯的黏滯損耗；強衰減介質中的地震波各頻率成分的能量嚴重衰減。

圖18 兩層模型不同機制下單道記錄（a）及振幅譜（b）對比

4 結論

本文基于頻率—空間域25點優化差分算法實現了強衰減模型波動方程的數值模擬，通過對比分析不同物性條件下地震波的衰減特征，模擬了淺表覆蓋低速層的雙層介質模型的地震波場，可以得出如下結論。

（1）頻率域波場模擬能得到全頻帶范圍內包含所有時刻波場信息的單頻切片，用于分析不同頻率的波場特征。不同頻率的單頻切片由于地震波波長不同，其波場形態不同。相同頻率的縱波和橫波因傳播速度的差異，單頻切片中波前面的疏密程度差異很大。由于介質對地震波各頻率成分的強吸收衰減作用，強衰減介質中地震波的頻率—空間域波場相比于完全彈性波場信息變得模糊。

（2）隨著介質孔隙度和流體黏度的增大以及介質黏滯性的增強，地震波能量衰減和速度頻散現象越來越明顯。孔隙度、流體黏度和介質黏彈性對地震波吸收衰減的影響程度不同。對于近地表介質，孔隙度的影響最大，介質黏彈性次之。在三種影響因素中，介質黏彈性是導致地震波頻帶變窄、主頻減小的關鍵，孔隙度和流體黏度對地震波主頻的影響不大，主要導致地震波各頻率成分尤其有效頻帶范圍內能量的衰減。

（3）基于強衰減模型所模擬的縱波和橫波在不同孔隙度、不同流體黏度和不同介質黏彈性條件下的衰減規律存在差異，與實際情況相符。強衰減模型能有效克服達朗貝爾模型中縱波和橫波衰減機制差異不大的缺陷。

（4）對比上覆低速層分別為完全彈性、黏彈性和強衰減介質的兩層介質模型的模擬波場可知，強衰減模型綜合考慮了介質的多種物理因素，描述的近地表介質對深層波場信息的嚴重干擾更符合實際。所以基于強衰減模型研究近地表介質的強吸收衰減，能為地震數據處理中的Q 值反演和衰減補償提供理論基礎。