社會網絡下分配眾包任務的真實機制

秦海燕，章永龍，李 斌*

（1.揚州大學廣陵學院，江蘇揚州 225000；2.揚州大學信息工程學院，江蘇揚州 225000）

（*通信作者電子郵箱bl@yzu.edu.cn）

0 引言

在眾包中，任務被外包給一組不確定的工人而不是指定雇員。Amazon Mechanical Turk 是一個功能性的眾包平臺，在這個平臺上，任務請求者發布翻譯、標記等任務，瀏覽眾包平臺的網民能夠完成這些小型任務，并且獲得少量的報酬。盡管只有小額報酬，兼職或全職雇傭者還是愿意承接不同類型的任務。這不僅比任務請求者線下雇傭員工的成本低，而且有助于提高工作質量。

值得注意的是，很少有關注眾包工人之間社會網絡的研究。以往的研究中，科學協作網絡被認為是一種具有代表性的社會網絡，其中團隊合作是科學協作的研究要點［1］。有些研究項目過于復雜，由一個科學家完成不了。因此，科學項目的開展必然需要許多科學家的合作，他們能根據自己的研究主題和興趣形成或建立社區。社會網絡為社會工作者之間的合作提供了一個可用的平臺。牛津英語詞典可以被看作一個大規模的眾包任務［2］。可以想象，如果牛津英語詞典出版商雇傭的工人彼此熟悉，他們一定會更有效地編纂詞典。眾包中，TopCoder是一個具有代表性的軟件開發眾包市場，每個項目都需要一個團隊相互合作共同完成。事實上，在眾包中考慮工人之間的社會網絡，工人、任務請求者和平臺都將獲利。對工人來說，他們寧愿與熟悉的人合作，也不愿與那些需要進一步磨合的人合作。這樣，這項任務就會更出色、更有效地完成。任務請求者也會很高興接收到更高質量的結果。文獻［3］也特別指出了工人完成眾包任務過程中質量的重要性。此外，平臺可以雇傭更少的工人，從而降低成本。

眾包任務按其復雜性可分為復雜任務和簡單任務［4］。本文討論了眾包中復雜任務的分配問題，并且眾包工人之間存在社會聯系。首先，任務請求者將一個必須由多個專業員工完成的任務發布到眾包平臺上，同時還會提交一個報價，這是任務請求者愿意支付的最高報酬。然后，平臺將任務公布在社會網絡上。在平臺上，具備完成該任務單個或多個技能的工人將申請該任務。接著，平臺將執行拍賣策略，將任務分配給某個團隊。工人完成任務之后，任務請求者將通過眾包平臺付款給團隊成員。任務請求者最終的支付不能高于自己的報價，也不能低于團隊的要價。這種場景下，仍有幾個挑戰。首先，社會網絡中任務分配問題已經被證明是NP 難問題［5］，因此，提出一個計算有效的機制是最重要的問題。除此之外，社會網絡中工人之間互連關系是十分復雜的。因此，該機制還應該利用好工人之間的社會聯系，找到一個合適的團隊來完成任務。最后，自私的工人可能會謊報他們的要價，以獲得更高的效用。因此，該機制必須確保是真實的。

針對上述問題，本文提出了一種社會網絡下分配眾包任務的真實機制（Truthful Mechanism for Crowdsourcing task assignment in Social Network，TMC-SN）。該問題被模擬成一個拍賣，其中任務請求者是買家，工人是賣家，眾包平臺充當拍賣者。任務請求者發布任務，相連的工人提交技能后，眾包平臺將進行分配。TMC-SN 提出了一種能在多項式時間內有效分配任務的方法。為了找出最合適的團隊，TMC-SN從邊際貢獻和團隊凝聚力兩個方面來衡量工人對團隊的適應性。與此同時，本文還考慮到了自利的參與者，他們可能為了獲得更高的效用而謊報自己的價值。因此，拍賣被成功引入到TMCSN 機制中來防止參與者謊報。TMC-SN 滿足拍賣的所有屬性，包括真實性、個體理性和預算平衡性。

1 相關工作

任務分配是眾包中最重要的過程之一［2］。以任務分配為中心，相關工作可分為兩類：1）有或沒有拍賣的任務分配；2）有或沒有團隊合作的任務分配。

1.1 有或沒有拍賣的任務分配

空間眾包是眾包的熱點問題之一。在該場景下，Hassan等［6］提出了一種基于組合分式規劃方法的距離可靠性比（Distance-Reliability Ratio，DRR）算法和一種擴展算法DRRUCB（DDR based on Upper Confidence Bound），當工人可靠性未知時，該算法利用區間評價啟發式算法來近似工人的可靠性。Cheng等［7］針對多技能空間眾包問題，提出了三種有效的啟發式方法，分別是貪婪、分治和基于成本模型的自適應算法。同樣地，文獻［8-9］都提出了貪婪算法來近似求解空間眾包中任務分配的問題。盡管上述方法能夠有效地解決任務分配問題，但是忽略了自私的參與者，他們可能會謊報價值以提高自身效用。TruTeam 算法［10］是眾包環境下典型的組建團隊來完成眾包任務的真實機制。TruTeam 算法采用了關鍵支付來確保參與者的真實性。因此，引入激勵機制來激勵并約束工人是必要的。

1.2 有或沒有團隊合作的任務分配

Yue 等［11］在任務請求者的預算內組建了虛擬團隊來完成任務，并聲稱是最佳匹配。雖然他們提到了團隊合作的重要性，但在算法中并沒有體現工人之間的團隊合作。同樣，TruTeam 算法［10］考慮了工人單個技能的邊際貢獻，但是團隊合作被忽略了。Xu等［12］提出了三種眾包模式，并且為這三種模式設計了一個真實的任務分配機制，它遵循匹配的方法來解決每一個模型的價值最大化分配問題。他們雖然考慮了任務請求者的偏好和工人工作量的限制，但沒有提及團隊合作。當完成宏任務時，比如編寫文檔、設計產品或開發軟件，這些任務比微任務需要更多的時間和經驗，互助的團隊合作也就顯得尤為重要［13］。Wang等［14］研究了復雜任務分配，處于社會網絡中的工人最終形成團隊完成了任務。他們強調最終形成的團隊，成員之間的社會網絡必須是連通的。因此，要高效地完成任務，團隊合作是必須要考慮的。

2 問題描述

2.1 系統模型

任務請求者：任務請求者可以在平臺上發布任務R，以及任務R的報價b。b是任務R被成功完成后的預估價值，可以不等于任務的真實價值b～。假設，任務請求者現需要τ種技能，S={s1，s2，…，sτ}，來完成任務R。是一個τ維的集合，其中表示完成任務R是否需要第k個技能sk。SR′是未被覆蓋的技能集合，SR′一開始等同于SR，隨著工人加入團隊，SR′會更新。

工人：每一個工人ai∈A都會提交一個元組Ci=給平臺。在Ci中，表示ai是否具備第k個技能，而是ai貢獻技能sk期望的獎勵。不一定等于ai貢獻技能sk的真實成本。C={C1，C2，…，Cm}是所有工人的競標信息。考慮到工人之間的社會網絡，用Nei(ai)來表示與ai直接相連的工人集合。

對于任務R，工人可以貢獻一個或者多個技能。因此，引入總成本oCi的概念來表示工人貢獻的總的技能成本。H={h1，h2，…，hτ}代表技能集合S的權重，hk表示貢獻技能sk所需付出的工作量。如果ai所具備的技能在SR′中是未被覆蓋的狀態，ai總成本的計算方式如下：

平臺：任務請求者和工人提交相關的信息給平臺之后，平臺輸出拍賣的結果，包括最終完成任務的團隊成員T?A，團隊成員的支付集合P={p1，p2，…，pm}。

任務請求者的效用等于完成任務的真實價值與最終支付給團隊的總報酬之差：

同樣地，被雇傭的工人ai∈T的效用等于拍賣平臺給的報酬與付出的成本之差：

2.2 相關定義

本節介紹幾個TMC-SN 預期需要滿足的經濟屬性以及后面將使用的一些概念。

定義1真實性。一個拍賣是真實的，表明不論買家還是賣家都不能通過謊報報價或者要價來獲得更高的收益。在TMC-SN 機制中，這表明，對于買家發布任務R，如果b=，UR是最大的；對于賣家?ai∈A，如果=oCi，Ui是最大的。

真實性是拍賣理論中最重要的屬性。既然公開真實的報價或要價能獲得最高的效用，理性的買賣雙方就不會出現謊報的行為。

Myerson定理［15］是拍賣中重要的理論，具體如下：

定理1Myerson 定理。一個拍賣是真實的，當且僅當同時滿足：

單調的分配規則：如果ai報價時被成功分配，那他報價時仍然能被分配。關鍵支付：關鍵支付作為ai的最終報酬，如果ai報價高于關鍵支付，那他就不能在拍賣中獲勝。

定義2個人理性。被成功分配的賣家得到的報酬高于其付出的成本，被成功分配的買家支付的金額低于其預算。換句話說，如果交易成功，對于?ai∈T，pi≥oCi；對于R，。

定義3預算平衡。預算平衡是指任務請求者的預算大于支付給工人的總報酬，即。

定義4社會福利。社會福利是所有成功被分配的買家、賣家和拍賣者的效用之和。社會福利也被認為是被成功分配的買方總價值和被成功分配賣方總成本之間的差額。

定義5計算有效性。當且僅當算法可以在多項式時間內執行時，該算法才是計算有效性的。

3 TMC-SN機制設計

3.1 詳細設計

一個團隊的表現會受多方面因素的影響。首先，任務請求者更偏愛貢獻力更大的員工。其次，文獻［16］指出，群體凝聚力與團隊的績效正相關。團隊越熟悉，相互之間磨合得越好，完成任務的質量也就越高。因此，綜合考慮工人的貢獻和工人之間的團隊凝聚力，給出如下定義：

定義6邊際貢獻。如果ai被選中進入團隊T，ai的邊際貢獻的值是ai對于未覆蓋的技能集合SR′所貢獻的工作量，即

定義7團隊凝聚力。如果ai被選中進入團隊T，團隊凝聚力的值是ai與團隊成員之間通信成本之和，即

定義8工人的適宜度。工人的適宜度與邊際貢獻和團隊凝聚力有關。因此，ai的適宜度fitness(ai)定義為：

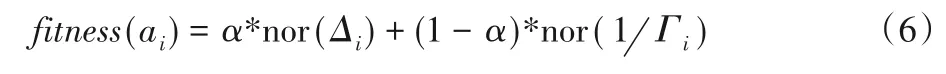
其中：α∈[0，1]是邊際貢獻與團隊凝聚力之間的調節參數；nor(·)是歸一化函數。

TMC-SN 機制如算法1 所示。在算法開始時，先搜索團隊成員的鄰居，并將其添加到Neis中。實現分配時，選擇單位工人適宜度成本最小的工人ai作為加入團隊的候選人，即候選人的在集合Neis中最小。可以肯定的是，候選人與團隊成員之間是有邊相連的。因為只有ai∈T的鄰居節點才可以加入團隊。換句話說，團隊成員在算法結束時會形成一個連通子圖。為了實現關鍵支付，在ai沒有參與的情況下重建團隊。這時，從{Neis′T}中選擇單位工人適宜度成本最小的工人aj，并且aj與現有的團隊成員之間仍然存在直接聯系。因此，

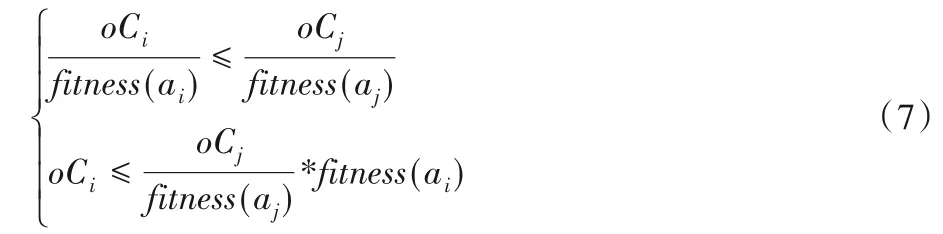
重復選擇aj，直到預算用完或者全部技能請求都得到滿足。迭代過程中，中的最大值會被作為ai的關鍵支付。此外，如果ai的關鍵支付低于剩余預算，ai才會被成功分配。迭代的過程中，一旦一個新的成員加入團隊，Δi、Γi和SR′將會更新。最后，如果任務R的技能需求被全部滿足，交易才是成功的。

算法1 TMC-SN機制。

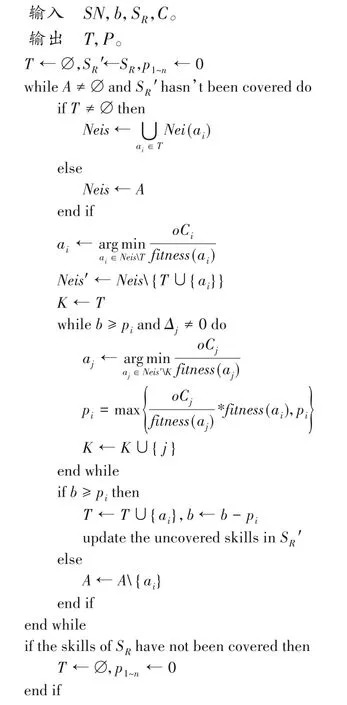
由算法1分析可得，TMC-SN 機制是計算有效的。從現有團隊中選擇團隊成員鄰居的時間復雜度是O(m)；選擇單位工人適應度成本最小的工人的時間復雜度是O(m)；定價階段的時間復雜度是O(mτ)；為了滿足所有的技能而進行了迭代，所以總的時間復雜度是O(m2τ)。因此，TMC-SN 機制是計算有效的。

3.2 理論分析

本節用理論證明了TMC-SN 滿足真實性、個體理性和預算平衡。

定理2TMC-SN滿足真實性。

證明 首先，任務請求者的真實性是顯而易見的。任務R不能被成功分配有兩種可能性：一種是R請求的技能不能被滿足；另一種是預算有限。如果是第一個原因，不論怎樣任務都不能被完成。如果一個預算有限的任務請求者想要被成功分配，那該任務請求者必須提高他的報價直至高于團隊的總報價。但是，這種情況下，任務請求者的效益肯定是負的。因此，理性的任務請求者不會謊報價格。

工人的分配和支付規則滿足Myerson 定理。首先，很顯然TMC-SN 的分配規則是單調的。如果ai報價時能成功被分配，他報價時也會成功被選中，這是因為ai單位適宜度的成本更小。

其次，ai的支付是通過選擇一個沒有ai參與的團隊來決定的。從集合Neis{T∪ai}選出aj，并且aj單位工人適應度的成本在該集合中是最小的。因此，可以得到式（7）。在的情況下，aj將會被選中，而不是ai。在這次迭代中，ai的報酬暫定為。

這時，pi′不是ai的關鍵支付，因為在Neis{T∪ai}中的競爭者沒有被全部考慮，并且任務R的技能請求沒有完全被滿足。因此，繼續迭代直到所有的技能都被滿足，或者預算被耗盡。最終ai的報酬pi為關鍵支付。

在這種支付規則下，如果ai報價高于pi，ai將被放置在最后被選中的工人的后面，最終ai將不會被選中。

綜合考慮單調的分配規則和關鍵支付，工人的真實性得證。

定理3TMC-SN滿足個體理性。

證明 對于任務請求者，每次新加入工人到團隊之前都會核查b≥pi是否成立，并且每次成功加入新成員之后預算都會更新。換句話說，剩余預算總高于新加入成員的報酬。因此，UR=b-≥0成立。

對于工人，由式（7）可得oCi≤pi，由此可得Ui=pi-oCi≥0。

綜上，TMC-SN滿足個體理性。

定理4TMC-SN滿足預算平衡。

證明 根據支付規則，每次新加入一個工人之前，剩余預算都會被核算是否足夠支付該工人的報酬。因此，有b-≥0，即預算高于團隊的總報酬。因此，TMC-SN 滿足預算平衡。

4 性能評估

本章模擬了眾包平臺，并且工人們處于一個社會網絡中。實驗進一步驗證了TMC-SN 滿足真實性；還觀察到調節參數α對交易數、團隊凝聚力、效用和社會福利的影響；并且，從交易數、效用、社會福利和成功率等方面，將TMC-SN 機制與不考慮社會網絡的TruTeam機制［10］進行了比較。

4.1 參數設置

工人數量m從10 變化到100，默認值為50。任務請求者的報價隨機分布在（0.5，6.5］上。工人對單一技能的要價在區間（0，1］中隨機取值。如果E(ai，aj)=1，則D(ai，aj)在區間［2，12］內變化。假設任務請求者最多請求6 種技能。調節參數α分布在間隔［0，1］中，默認值為0.5。圖示中的某些數據是1 000個獨立實例的平均結果。在每個實例中，只有一個任務請求者發布一個任務。

4.2 真實性

在任務請求者和工人中隨機選擇一個贏家和一個輸家，然后在他們報價和要價變化時計算效用。如圖1（a）所示，一個成功被分配的任務請求者若以b==4.57 真實報價，獲得的效用是2.13。當該任務請求者試圖降低他的報價以獲得更高的效用時，他將變成失敗者并且效用為0。圖1（a）中失敗的任務請求者的情況表明，當一個原本失敗的任務請求者想提高報價贏得拍賣時，他獲得的效用將從0 變為負數。圖1（b）表明，當一個獲勝的工人要價oCi==0.156 時，獲得的報酬是0.679，效用為0.523。當工人想通過提高要價來增加效用時，效用在開始時保持在0.523。然而，當他的要價變為0.61 時，他將成為一個失敗者，效用為0。圖1（b）還表明，當一個失敗的工人要價oCi==0.535 時，工人未被成功分配，效用為0。如果他將要價降低到0.195，他將以負效用-0.081 贏得拍賣。換而言之，任務請求者或工人不能通過謊報他們的報價或要價而獲益。

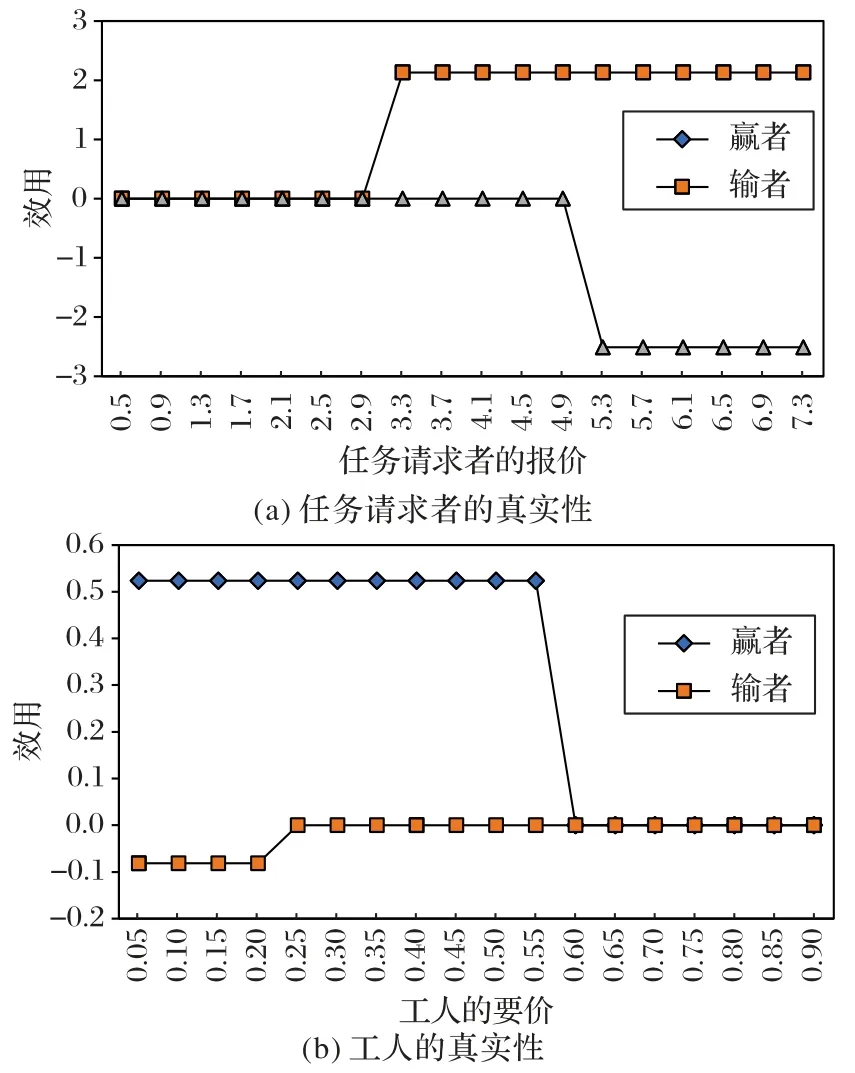
圖1 TMC-SN真實性驗證Fig.1 Verification of TMC-SN truthfulness

4.3 調節參數α對性能的影響

在TMC-SN 機制中，工人對任務的適宜度綜合考慮了邊際貢獻和團隊凝聚力。其中，α是這兩個因素的調節參數，因此，α對TMC-SN機制的性能有一定的影響。實驗數據中的交易數是指1 000 個獨立實例中成功交易的數量。圖2（a）顯示交易數隨α的增大而增加。當α增大時，邊際貢獻在工人適宜度中的重要性增加，相應地，團隊凝聚力的重要性降低。因此，對團隊凝聚力的關注會降低交易數。圖2（a）還可以看出，當α增加時，團隊凝聚力先增加，在α=0.4 左右達到最低點，然后波動上漲。團隊凝聚力的值是團隊通信成本之和。也就是，α越小，通信成本越小，工人之間的聯系也就越緊密。圖2（b）表明，隨著α的增加，任務請求者的效用增加，而工人的效用卻減少了。這是因為α越大，交易成功率會提高，任務請求者被成功分配的概率也就會提高，獲得的效用相應地提高，而工人卻因此獲得了更低的效用。圖2（c）中，可以觀察到，當α增加時，社會福利將減少。這意味著對團隊凝聚力的關注有利于社會福利的增長。但是，隨著更多工人的參與，社會福利會更少。這是因為團隊中的工人越多，對預算的分擔就越充分，社會福利就會降低。

4.4 TMC-SN與TruTeam對比

本節將TMC-SN 機制與TruTeam 機制［10］進行了比較。在TruTeam 機制中，忽視了工人之間的社會關系。在這種情況下，工人的適宜度只與邊際貢獻有關，即α=1。從圖3（a）可以看出，隨著工人數量的增加，TruTeam 的交易數總是高于TMC-SN。這是因為TMC-SN 考慮了工人的團隊凝聚力，交易的限制更嚴格，成交率就更低。圖3（b）表明，任務請求者的效用隨著工人的增加而提高，而工人的效用則降低。另外，TruTeam 中任務請求者的效用優于TMC-SN，而工人的效用低于TMC-SN。這表明關注團隊凝聚力的對工人是有利的，但對任務請求者是不利的。圖3（c）可看出TMC-SN 和TruTeam 的社會福利是波動的。然而，從整體上看，TMC-SN 的社會福利優于TruTeam。對團隊凝聚力的關注有利于提高社會福利。

此外，還比較了TMC-SN與TruTeam 的成功率。成功率是指團隊完成任務的概率。如果ai和aj相連，則在區間（70%，100%）中隨機選擇兩者共同完成任務的成功率；如果不相連，則在間隔（40%，70%）中隨機選擇兩者的成功率。顯然，如果兩個工人相連，成功完成任務的幾率大于不相連的情況。圖3（d）中所示的數據是所有團隊成員之間成功率的乘積。結果表明，隨著工人數量的增加，成功率降低，但TMC-SN 的成功率始終高于TruTeam。顯然，對團隊凝聚力的關注提高了任務完成的可能性。

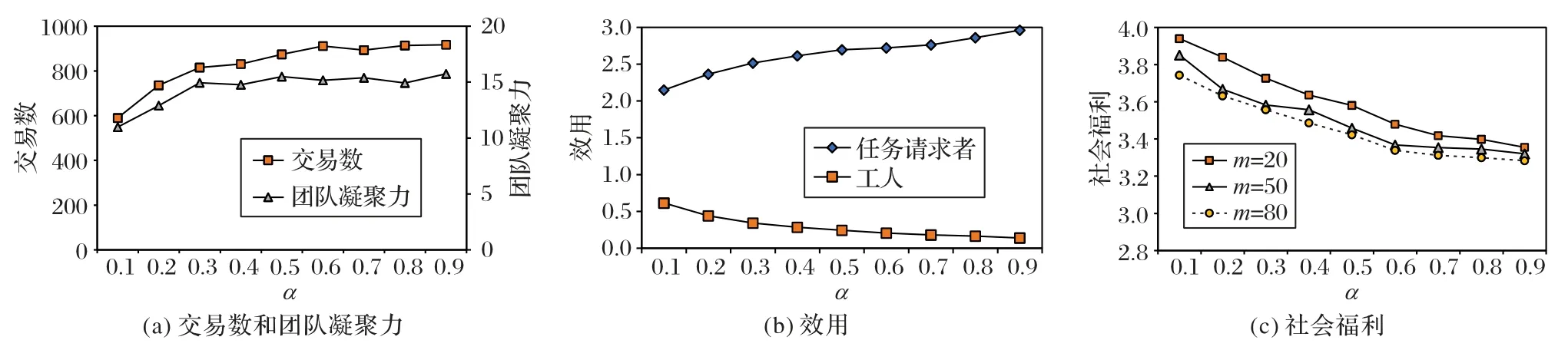
圖2 調節參數α對性能的影響Fig.2 Influence of α on performance

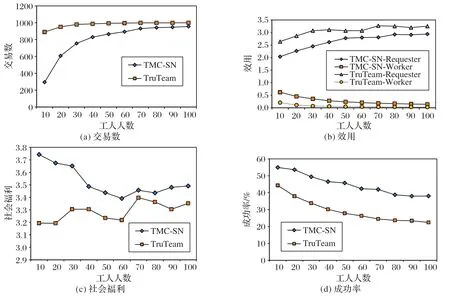
圖3 TMC-SN與TruTeam的比較Fig.3 Comparison of TMC-SN and TruTeam

5 結語

本文將社會網絡下眾包任務分配的問題模擬成一個拍賣，其中任務請求者是買家，工人是賣家，眾包平臺充當拍賣者，并提出TMC-SN 機制以解決該模型下的一些挑戰。為了找出最合適的團隊，TMC-SN從邊際貢獻和團隊凝聚力兩個方面來衡量工人對團隊的適應性。理論分析證明TMC-SN 滿足真實性、個體理性和預算平衡。在性能分析階段，進一步驗證了TMC-SN 滿足真實性，還觀察了調節參數α對性能的影響，并比較了TMC-SN 和TruTeam 的性能。實驗結果表明，TMCSN機制在社會福利方面具有優勢，并且對工人有利。