拱頂罐VOCs排放影響因素研究
趙明婕
(中石油燃料油有限責任公司,北京 102200)
VOCs是形成高臭氧濃度的光化學煙霧和高濃度PM2.5霧霾的關鍵[1],易引發呼吸系統的疾病,危害人體健康。在石油石化企業中VOCs的主要來源是儲罐無組織排放、生產裝置泄漏。我國在2011年首次提出“嚴格控制揮發性有機污染物排放”的政策要求[2],2015年國家發展改革委在《揮發性有機物排污收費試點辦法》中要求各直轄市、各省及計劃單列市環保主管部門負責征收VOCs排污費,確定石油化工行業作為試點。
據此,石油石化企業無組織排放量的準確核算一方面是制定企業大氣環境防護距離和保障居民健康的必要條件,另一方面也是保障企業經濟效益和科學制定污染防治措施的重要前提。目前現行無組織排放量的核算方法有四種,分別來自美國環保署、美國石油學會、《石油庫節能設計導則》和中國石油化工系統。然而這些核算方法多樣且準確度各異,同時缺少風險評估及預防改善措施的數學模型依據,這些問題成為環評和石油企業設計過程中的難點和重點[3]。本文采用數值模擬方法,結合Fluent軟件完成多相流模型和質量傳遞模型,研究拱頂罐在不同進油速率和不同罐內初始濃度條件下,儲罐內部油氣擴散規律,對比二者對拱頂罐呼吸損耗的影響,為拱頂罐損耗量核算提供重要參考。
1 數值模擬模型建立
1.1 幾何模型及控制方程
應用ICEM軟件建立如圖1所示的拱頂罐幾何模型,建立二維計算域,采用多相流(VOF)模型和RNGk-ε模型。規定水平向右為X軸正方向,進油方向沿X軸負方向,垂直于X軸向上為Y軸正方向。拱頂罐進油口直徑為20 cm,呼吸閥直徑為25 cm,儲罐直徑為23.7 m,罐高為12.7 m,拱頂曲率半徑為5.8 m,進油口距罐底40 cm。模擬中對呼吸過程揮發的油品混合物進行簡化,設置為乙烷氣體為第一項,空氣為第二項。
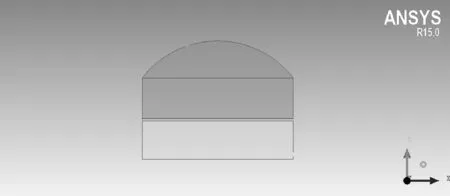
圖1 拱頂罐幾何模型Fig.1 The geometric model of dome roof tank
模擬采用多相流(VOF)模型和RNGk-ε模型,其中,油罐底部裝油的流動過程采用多相流模型計算,氣-液相界面可以通過多相流(VOF)模型中體積分數的連續性方程的計算來確定,如式(1):
(1)
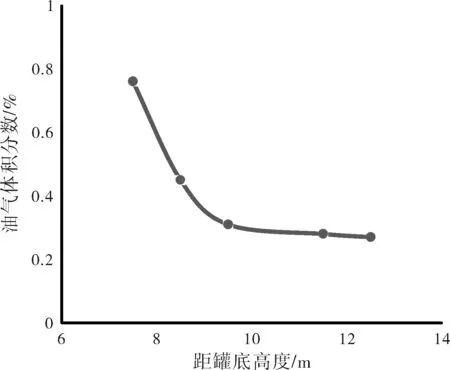
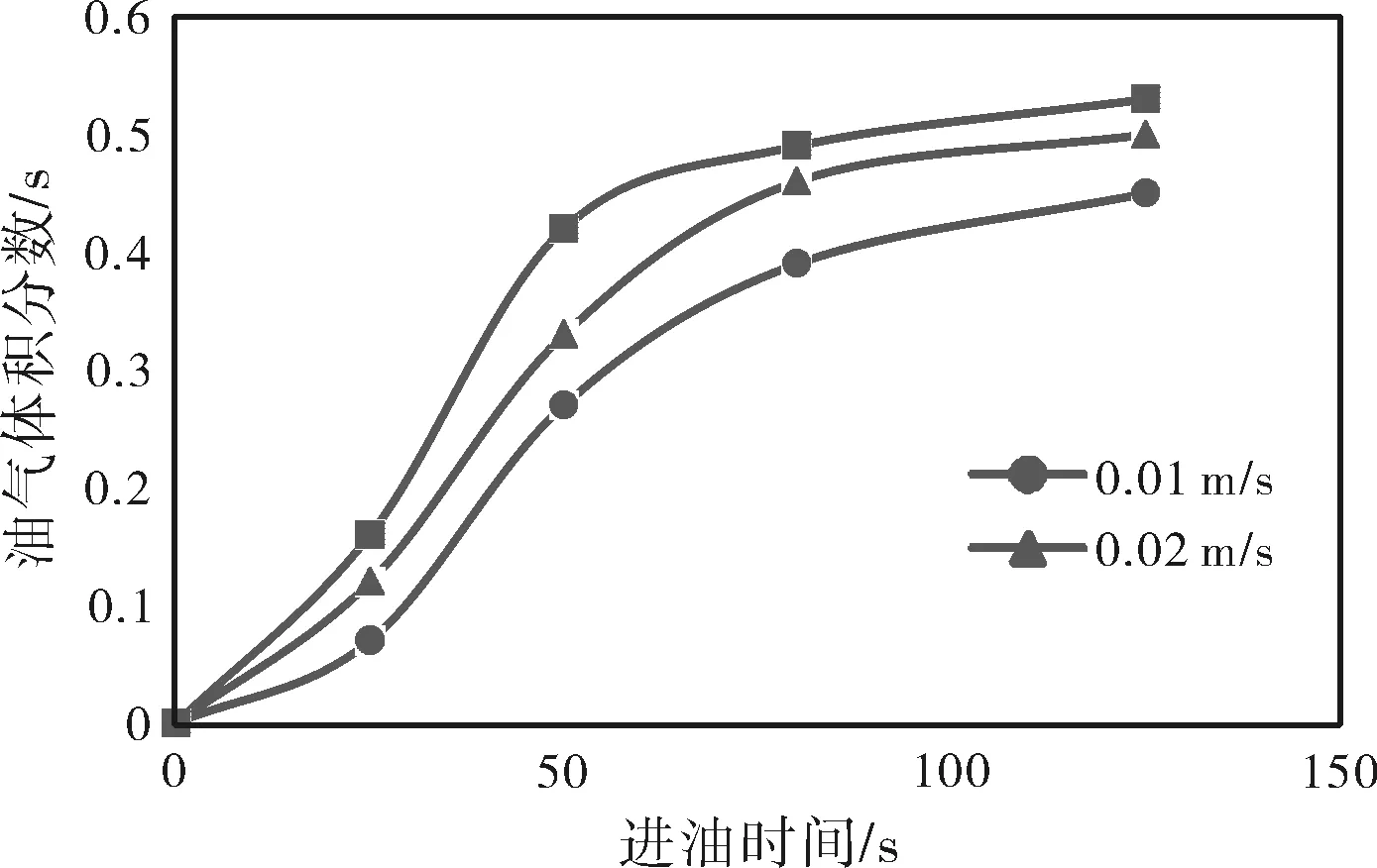
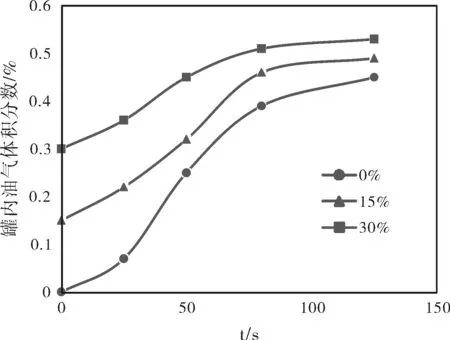
當計算網格內全部是液相時,a=0,反之充滿氣相時則a=1。當0 (2) (3) 其中的ρ和μ由平均體積分數確定,如下式: ρ=αpg+(1-α)ρ1 (4) μ=αμg+(1-α)μ1 (5) 壓力梯度會由于氣—液相界面的表面張力而存在,在平衡狀態下其數值等于動量方程中的體積力,如下式: (6) 式中:α為體積分率;t為時間,s;ε為重力加速度,m/s2;x為運動距離,m;ρ為密度,kg/m3;u為速度,m/s;fσ為體積力,N/(m3·s);μ為動力粘度,Pa·s;ν為運動黏度,m2/s。 油罐底部裝油屬于湍流流動,本模擬過程中利用RNGk-ε模型作為湍流方程,模型如下式,其中,常數σk=1.0;σε=1.2;Cμ=0.09;C1ε=1.44;C2ε=1.9。 (7) (8) (9) (10) 式中:A為氣液相界面體積,m2;K為湍動能,m2/s2;ε為耗散率,m2/s2;σ為表面張力;GK為由于層流速度梯度而形成的湍流動能,m2/s2;Gb為浮力形成湍流動能,m2/s2。 選用非定常模型,重力設置為-9.8 m/s2,采用SIMPLE算法,在氣—液交界面處,引入如下式所示的用戶自定義函數(簡稱UDF)的方法[6]來解決以上問題,即命名一個質量源項,也就是選取氣液體共同存在的網格單元作為飽和油氣質量分數層。流場內全部采取結構化網格劃分,以Determinant 3×3×3為評價標準進行網格質量檢查,均滿足標準要求。當滿足進出口質量相對誤差小于5%,且連續性方程殘差界限設不超過10-5的條件時,即可認為計算收斂。 (11) (12) 式中:xoilgas為油氣的摩爾分數;Moilgas為油氣的分子質量,kg/mol。 由于本模擬忽略了外界環境溫度的變化對油品蒸發速率的影響、實驗的環境條件等因素共同限制,不可避免地促使實驗測量值與模擬值之間存在一定誤差。但是模擬過程時間短,溫差變化較小,保證了模擬與實驗結果的可靠性。從表1不同高度時油氣體積分數隨時間的變化可知,在同一時刻油氣體積分數都是隨高度的升高而降低。且由圖2油氣體積分數隨距罐底高度的變化可知,縱向油氣濃度分布曲線有一個比較明顯的拐點,靠近油液面附近存在高濃度層,油氣濃度沿高度變化比較顯著,距離油液面較遠處油氣濃度較低,但濃度隨高度變化分布均勻,符合罐內縱向油氣體積分數的分布基本規律[7],說明了模型的準確性。 表1 不同高度時油氣體積分數隨時間變化的模擬值Table 1 Simulated values of oil and gas volume fraction over time at different heights 圖2 油氣體積分數隨距罐底高度的變化Fig.2 The oil and gas volume fraction at the different height from the bottom of the tank 國外內四種核算方法中損耗量皆隨周轉量的增大而明顯增加[8],而進油速率是周轉量大小的主要影響因素,由于液面高度的變化以及氣體間的存在,強迫對流占主導地位的傳質過程[9]。因此可看出進油速率是拱頂罐呼吸損耗量核算公式的一項重要參數。 模擬不同進油速率時拱頂罐呼吸閥處油氣體積分數變化。圖3表示進油速度為0.01 m/s、0.02 m/s和0.03 m/s時呼吸閥處的油氣體積分數云圖。進油速度同為0.01 m/s,進油時間為50 s時呼吸閥處油氣體積分數為27%;80 s時,呼吸閥處油氣體積分數為39%,累計時間125 s時呼吸閥處油氣體積分數增加到45%;進油速度為0.02 m/s,選取相同的時間點發現呼吸閥處油氣體積分數分別為為33%、46%和50%;進油速度為0.03 m/s,呼吸閥處油氣體積分數分別為為42%、49%和53%。由圖4油氣體積分數隨進油速率的變化曲線可知,在進油速度較小的情況下,呼吸閥處油氣體積分數變化比較平緩,隨著進油速度的加快,呼吸閥處油氣體積分數達到飽和程度的速率也同步加快。這是因為隨著罐內液面的不斷升高,壓縮罐內上部空間的混合氣,裝油過程的進行使得呼吸閥處的油氣體積分數不斷增加,單位時間內壓縮的體積增多,最終達到飽和狀態。 圖3 不同進油速率時呼吸閥處油氣體積分數Fig.3 The oil and gas volume fraction contour at different oil inlet speed 圖4 油氣體積分數隨進油速率的變化Fig.4 The oil and gas volume fraction at different oil inlet speed 模擬在不同罐內初始油氣濃度條件下拱頂罐呼吸閥處油氣體積分數變化。如圖5表示在進油速度為0.01 m/s,罐內初始濃度分別為0%、15%和30%時呼吸閥處的油氣體積分數云圖。初始濃度為15%,進油時間為50 s時拱頂罐呼吸閥處油氣體積分數為32%,85 s時為46%,125 s時為49%;初始油氣濃度為30%,選取相同的時間點發現拱頂罐呼吸閥處油氣體積分數分別為45%、51%和53%。由圖6油氣體積分數隨罐內初始油氣體積分數的變化可知,罐內初始油氣體積分數值增大,油氣體積分數增長的速率越緩慢,這是由于罐內初始油氣體積分數增加,罐內油氣體積分數較初始濃度為0%時梯度減小,蒸發速率減緩,油氣質量分數的變化曲線隨初始油氣體積分數的升高而變緩。 圖5 不同初始油氣體積分數時油氣體積分數Fig.5 The oil and gas volume fraction contour with different initial oil and gas volume fraction in the tank 圖6 油氣體積分數隨罐內初始油氣濃度的變化Fig.6 The oil and gas volume fraction with different initial oil and gas volume fraction in the tank (1)通過拱罐頂內油氣擴散進行模擬,繪制油氣體積分數隨距罐底高度變化的曲線可知,縱向油氣濃度分布曲線存在一個明顯的拐點,靠近油液面附近存在高濃度層,油氣濃度沿高度變化比較顯著,距離油液面較遠處油氣濃度較低,但濃度隨高度變化分布均勻。 (2)進油速率對罐內油氣擴散具有明顯影響,是拱頂罐呼吸損耗量核算公式的一項重要參數。在罐內初始油氣體積分數相同時,進油速率越大,罐內液面的不斷升高,上部空間的混合氣不斷被壓縮,當進油速率從0.01 m/s升高至0.03 m/s時,呼吸閥處油氣體積分數達到50%的時間從183 s縮短至80 s。 (3)在進油速率相同時,罐內初始油氣濃度越大,油氣濃度梯度越小,達到飽和的時間縮短,在罐頂空間內油氣體積分數的變化越平緩。當罐內初始油氣濃度從0%增加至30%時,呼吸閥處油氣體積分數達到50%的時間從183 s減少至66 s。結合初始油氣濃度對拱罐內油氣擴散也具有明顯影響的情況,建議將罐內初始油氣濃度作為拱頂罐呼吸損耗量核算公式的一項參數。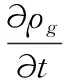
1.2 邊界條件及網格劃分
2 數值模擬結果分析
2.1 數值模擬模型驗證

2.2 進油速率的影響

2.3 罐內初始油氣濃度的影響

3 結 論

