基于MUSIC算法解兩相干陣型配置技術研究

2020-10-20 13:27:52張秋實王坤達丁兆貴

艦船電子對抗 2020年4期

張秋實，王坤達，丁兆貴，趙泉

(中國船舶重工集團公司第七二三研究所，江蘇揚州 225101)

0 引言

在現代電子戰當中，實現對電磁輻射源的定向都是利用天線陣列的陣列特性，因此天線陣列配置技術一直是電子戰領域內的研究重點。早期電子戰中應用的電磁信號通常頻率較低，且電磁環境不復雜，所以早期的測向系統主要采用均勻線陣的波束形成方法[1-2]。該方法具有計算簡便、易于實現等優點；但是陣列孔徑有限，因此波束寬度較寬，測向精度和分辨力都較低。然而隨著電磁信號應用的普及，電子戰中對雷達精度等需求的提升，當下電子戰的目標信號頻段非常高，普遍高于10 GHz，導致信號半波長小于1.5 cm，仍然使用均勻線陣會導致陣列的陣元間距小于1.5 cm；但是在一定的增益和波束寬度要求下，能夠達到的最小天線直徑仍然遠大于1.5 cm，而布置大于半波長的天線間距的均勻線陣則會導致嚴重的模糊，所以當系統的工作頻段特別高的情況下，均勻線陣并不適用。并且當下電子戰的電磁環境愈加復雜，會給系統帶來相干信號的干擾，使測向系統的性能急劇下降，難以滿足電子戰需求。所以，目前電子戰急需一種工作頻段足夠高、抗復雜電磁環境的測向接收機。

以MUSIC算法為代表的子空間類算法的出現，使得陣列天線的測向精度和分辨力大為提高，突破了瑞利極限[3]；因此，這類算法在近20年得到廣泛的關注，研究結果層出不窮。且利用MUSIC算法進行處理，能夠對相干信號進行來波方向估計，十分適用于解決上述問題；但是由于可以避開信號角度估計模糊問題，目前對MUSIC布陣形式的研究多集中在均勻線陣、均勻圓陣、立體陣、十字陣等形式上。文獻[4]、[5]提出了一種雙平行陣布陣形式，文獻[6]提出了一種五元圓陣形式。以上陣列布置形式雖然在特定條件下能夠滿足超分辨測向的條件，達到較好的性能，但是仍然有以下不足：

(1) 均勻線陣是把若干個陣元按照相同的陣元間距進行布署，并形成一種直線形狀的陣列。該陣列形式結構簡單，陣列流型符合Vandermonde矩陣結構。由于均勻線陣無模糊測試來波方向需滿足陣列間距小于等于最大工作頻率波長的一半，而目前電子戰來波頻率普遍大于10 GHz，半波長小于1.5 cm，遠小于有一定增益和波束寬度要求時能達到的最小天線尺寸。均勻線陣如選擇遠大于最小半波長的陣元間距時，就會產生嚴重的相位模糊，產生大量偽峰，導致算法難以分辨；而增加陣元數目將會極大增加設備成本，無論對處理的實時性還是設備的成本控制都會帶來極大的不良影響。

(2) 圓陣、立體陣、十字陣等陣列形式在譜峰搜索時均會采用二維搜索，計算量與一維搜索計算量成平方關系，十分巨大，并不適用于目前對信號實時處理要求越來越高的電子戰系統中。

(3) 目前大多數文獻中的非均勻線陣布置，大多存在較小的陣元間距、陣元數量過多以及無法克服復雜模糊等問題[7-9]。

本文研究了一種適用于解兩相干信號的超分辨陣列布置方法，該方法具有以下優點：

(1) 相對于均勻線陣，具有分辨力高、可適用于較高的工作頻段的優點；

(2) 相對于圓陣、立體陣、十字陣等面陣形式具有譜峰搜索時的計算資源少、計算實時性強的優點；

(3) 相對于現有的非均勻線陣的研究，具有最小陣元間距大于天線尺寸、針對兩相干信號陣元數最少、兩信號測向無模糊、陣列性能滿足工程系統要求等優點，為工作頻段足夠高、抗復雜電磁環境的下一代電子戰測向接收機創造了實現的基礎。

1 信號模型

當N個遠場窄帶信號以不同的入射角度輻射到一個由M個天線組成的陣列上時，第k個陣元接收信號為：

k=1,2,3,…,M

(1)

式中：gki為第k個陣元對第i個信號的增益；nk(t)為第k個陣元在t時刻的噪聲；τki為第i個信號入射到第k個陣元時相對參考陣元的時延。

將M個陣元在特定時刻接收的信號寫成矢量形式可得：

X(t)=AS(t)+N(t)

(2)

式中：X(t)=[x1(t),x2(t),…,xM(t)]T，為陣列的M×1維快拍數據矢量；N(t)為陣列的M×1維噪聲數據矢量；S(t)為空間信號的N×1維矢量；A=[a(θ1),a(θ2),…a(θn)]，為空間陣列的M×N維的陣列流型。

陣列的協方差矩陣為：

R=E[XXH]=AE[SSH]AH+σ2I=

ARsAH+σ2I

(3)

由于信號與噪聲互相獨立，數據協方差矩陣可分解為信號、噪聲相關的兩部分，其中Rs是信號協方差矩陣，ARsAH是信號部分。

對R進行特征分解，有：

(4)

式中:Us為由大特征值對應的特征矢量張成的子空間，也即是信號子空間；UN則為噪聲子空間。

而理想條件下，信號子空間的導向矢量與噪聲子空間正交：

aH(θ)UN=0

(5)

由于噪聲的存在，a(θ)與UN并不能完全正交，因此，實際上求DOA是以最小優化搜索實現的，則MUSIC算法譜估計公式為：

(6)

2 陣列信號模型

將若干個傳感器以一定的幾何形狀進行空間部署并用于接收信號的裝置稱為陣列。陣列的幾何結構可以按照陣元在空間上的擺放位置來劃分：

(1) 線陣：線陣是把若干個陣元按照一定的陣元間距進行布署并形成一種直線形狀的陣列。線陣按照排列間距的不同又可以分為均勻線陣和非均勻線陣。均勻線陣是指任意2個相鄰陣元的間距均相等，非均勻線陣的任意2個相鄰陣元間距則不完全相同[10]。

(2) 面陣：將陣列的天線按照一定的設計規則布置在平面上的陣列為面陣。

(3) 立體陣：陣列的天線不僅布置在一個平面上的形式為立體陣。

目前，針對陣型的研究多集中于均勻線陣上。但是目前電子戰中，信號頻段普遍高于10 GHz，導致信號半波長小于1.5 cm。而天線具有一定的固有尺寸，且天線間距過近會導致天線的耦合特別嚴重，影響陣列測向性能。當使用半波長作為陣元間距布置均勻線陣時，將會導致陣列的角度分辨能力大幅下降，難以達到指標要求。如果想得到足夠的角度分辨力，就需要更多的陣元數量，增加基線長度；但是，這種做法會造成陣元數量和后續的采樣、處理資源的浪費。面陣受限于其二維搜索時超大的計算量，對一些實時性要求高的測向需求并不適用；所以，非均勻線陣是最適用于目前超分辨測向系統的陣列方案。

非均勻線陣具有陣列陣元間距大、來波方向估計的分辨力較高、所用天線的數量更少等優點；但是由于陣列陣元間距均超過半波長的間距，就會引入信號模糊問題。對于任意陣列而言，其陣列流型矩陣表示如下：

(7)

而如果在視角范圍內存在：

a(θi)=a(θi′)，θi≠θi′

(8)

式中：θ表示入射角度。

當陣列設計不當出現上述情況時，就會在譜峰搜索的過程中搜索到非信號入射角度的譜峰，使系統誤認為是多信號入射。這種多個信號導向矢量相同的情況被稱為一般模糊。除此之外，設計不當的非均勻陣列還會存在特定角度的導向矢量是若干個其他導向矢量的線性組合的形式，這也會導致系統誤認為多信號入射，產生錯誤結果，被稱為復雜模糊，如式(9)所示：

(9)

陣元間距互質可以解決簡單模糊問題。滿足M≥N+1時，即可對來波方向進行估計，即對兩信號進行來波方向估計，理論上只需要3個陣元，但是由于噪聲和模糊的存在，利用非均勻三元線陣對兩非相干信號源進行估計的過程中，檢測概率并不理想。圖1為三元陣和四元陣對2個非相干信號不同信噪比下的檢測概率圖，其中每個信噪比進行1 000次蒙特卡洛實驗，2個信號的入射角度在-50°到50°之間隨機選擇。圖2為三元陣對2個非相干信號進行MUSIC計算得到的譜圖。

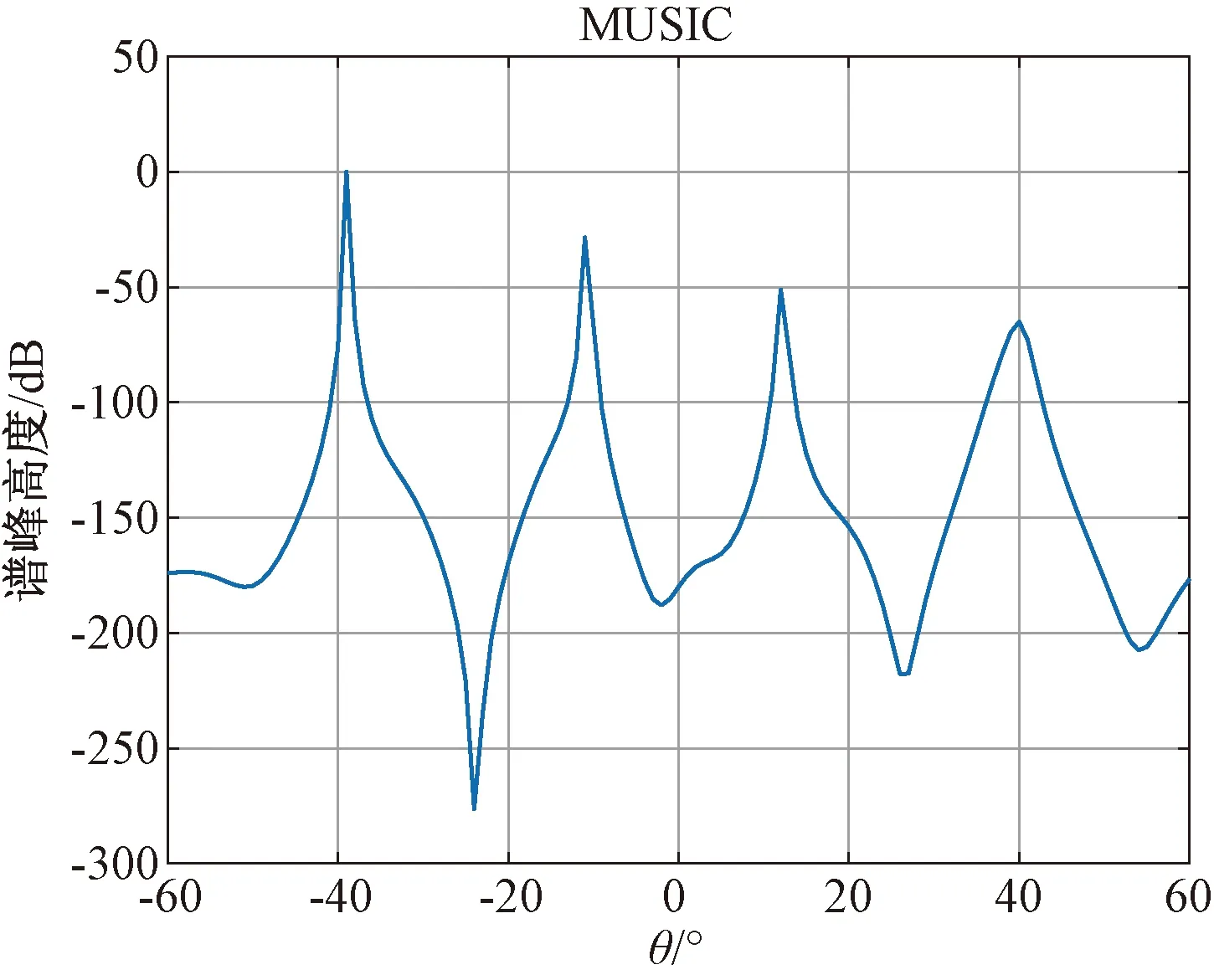
圖2 三元陣對2個非相干信號DOA模糊情況

從圖1中可以看出，利用三陣元對2個非相干信源進行估計時檢測概率遠遠弱于四陣元檢測能力；而從圖2中可以看出，是由于三陣元對2個非相干信源估計的結果中模糊情況十分嚴重導致的。而四元陣列檢測能力十分優異，所以在實際超分辨測向系統中，需要采用陣元間距互質的四陣元陣列形式。

陣元間距互質只能解決簡單的模糊問題，無法克服復雜模糊。所以并不能通過簡單選擇幾個互質間距解決陣列布置問題。通過計算機過度搜素可以得到性能優異、可以克服復雜模糊的陣列。

圖3(a)是過度搜索得到的陣列間距和簡單選取互質陣元間距情況下的檢測概率對比圖，每個信噪比點進行10 000次蒙特卡洛實驗，2個信號在-50°到50°之間隨機選擇，圖3(b)為圖3(a)在高信噪比時的局部圖片。從圖3可以看出，雖然復雜模糊對陣型檢測概率影響不大，但是復雜模糊出現則代表系統出現虛警情況，而虛警情況的出現會極大地增加設備和人員的工作量，產生很大代價，而通過計算機過度搜索得到的陣型，性能比簡單選擇互質間距陣型的檢測概率更高，且能夠突破復雜模糊的影響，在一定信噪比之上達到100%的檢測概率，更適用于測向系統。

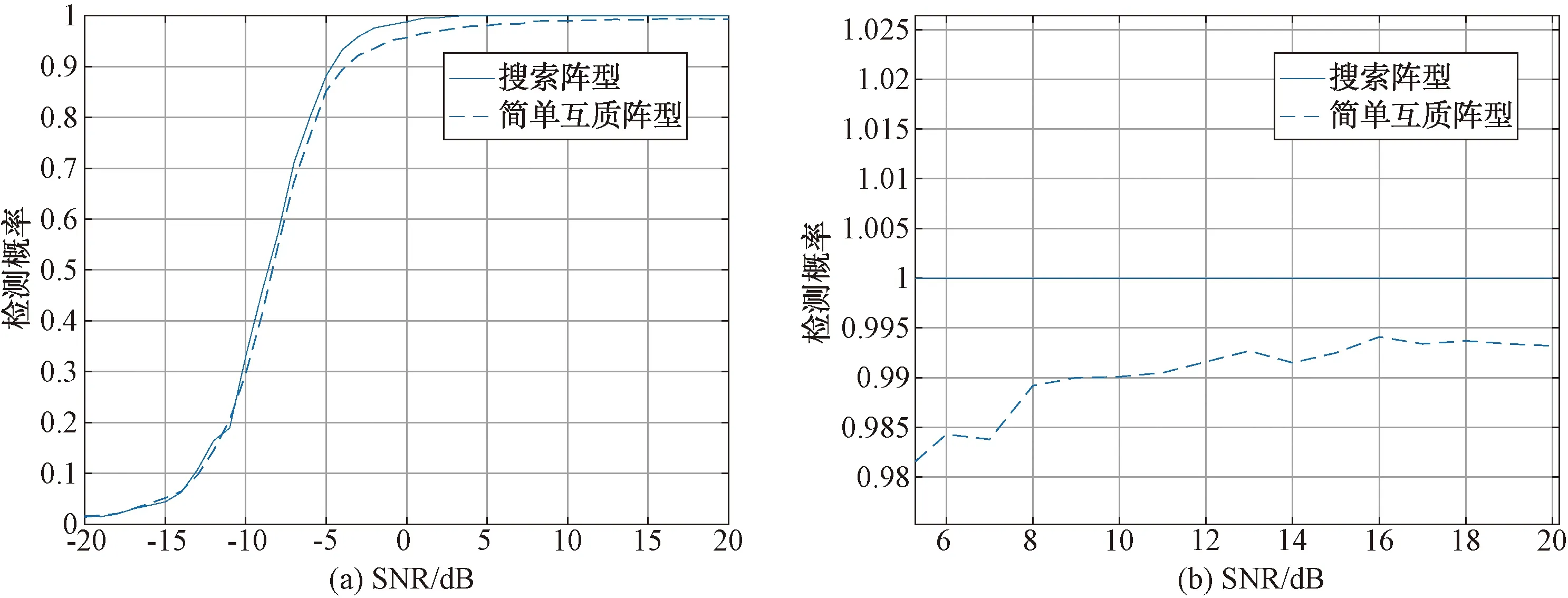
圖3 過度搜索得到的陣型和簡單互質陣型的檢測概率

3 相干信號陣列配置技術

四陣元線陣在非相干條件下具有很好的性能，但在信源相干時，由于陣列接受的數據協方差矩陣的秩降為1，導致信號子空間的維數小于信源數，這會導致某些信號的導向矢量與噪聲子空間不完全正交，從而無法正確估計信源方向。目前，關于解相干的處理基本有空間平滑法、矩陣重構法以及以Toeplitz法為代表的非降維法。其中，空間平滑法由于易于實現、計算量小且可以適用于非等距線陣成為解相干系統的首選方案。

非等距線陣與等距線陣不同的是不能通過增加1個陣元得到多個子陣，所以增加子陣數量就會增加大量的陣元數量。在2個相干信源的情況下，理論上通過2個子陣就可以較好地估計，所以2個子陣平滑測向方案為成本最低方案，可以在以非等距四元陣作為基礎子陣的情況下，增加若干陣元達到2個子陣的平滑效果。

空間平滑法是利用陣列流型的平移不變性構造相同的陣列流型的方式，如圖4所示，1～4陣元和5～8陣元的陣列流型相同，所以可以通過兩矩陣數據協方差矩陣平滑修正的方式得到滿秩協方差矩陣，對兩相干信源進行方向估計。

圖4 兩子陣平滑陣型1

但是可以看出，圖4的平滑方法用了8個陣元，四陣元與五陣元之間的陣列孔徑對該方法并無影響，所以可以復用1個陣元進一步減少陣元數量和后續計算量。

從圖5中可以看出，利用前向平滑可以復用1個陣元。從圖6可以看出，利用后向平滑卻可以復用2個陣元，進一步減少解相干系統成本。

圖5 兩子陣平滑陣型2

圖6 兩子陣平滑陣型3

4 性能仿真及無法解算問題

圖7是3種陣型在信噪比-20 dB到20 dB之間的檢測概率圖，每個信噪比點進行10 000次蒙特卡洛試驗，每次蒙特卡洛試驗的信號入射角度在-50°到50°之間隨機選擇。從圖7中可以看出，3種陣列布置方式的檢測概率區別不大，方法3可以復用2個陣元，陣元數量和系統成本最低，可以作為解兩相干信號系統的陣列布置。

從圖7和圖3中可以看出，其相干信號檢測概率小于其非相干信號檢測概率。其主要原因是：理論上平滑過程中可以將協方差矩陣的秩恢復，但是在一定信噪比下會有(1+ejk(β2-β1))≈2的情況出現，導致：

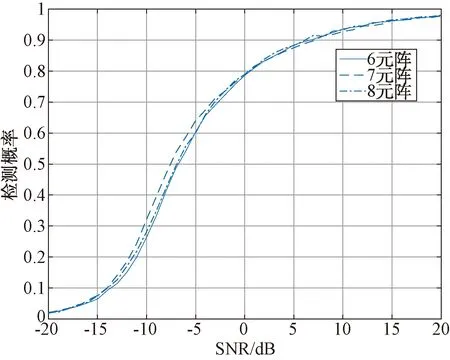
圖7 3種陣列布置方法檢測概率圖

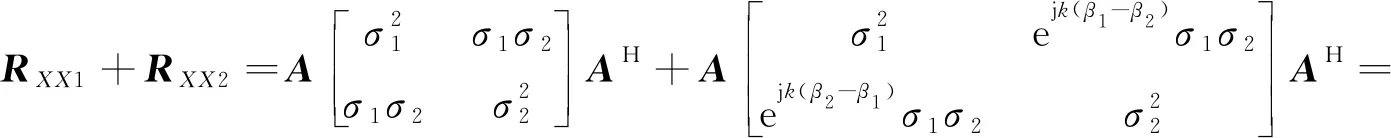
(10)

矩陣分解的特征值結果為1個大值和若干個相差不大的值，無法進行特征值判定的情況出現，導致無法解算現象的出現，降低了系統的檢測概率。改善該問題的方法為增加子陣、改善平滑算法等。增加子陣數量可以有效緩解該問題的發生，但是增加子陣數量會極大地增加系統成本。綜合考慮性能和成本，兩子陣解兩相干信號仍為性價比最高的方案。

5 結束語

本文針對實際工程應用中，當工作頻段過高時，均勻線陣MUSIC測向算法所需的天線間距過小，且小于天線尺寸，難以適用于實際工程的不足，研究了一種適用于解兩相干信號的超分辨陣列布置方法。該方法具有以下優點：