基于深度Q網絡的水面無人艇路徑規劃算法

隨博文　黃志堅　姜寶祥　鄭歡　溫家一

摘要：為實現水面無人艇（unmanned surface vessel， USV）在未知環境下的自主避障航行，提出一種基于深度Q網絡的USV避障路徑規劃算法。該算法將深度學習應用到Q學習算法中，利用深度神經網絡估計Q函數，有效解決傳統Q學習算法在復雜水域環境的路徑規劃中容易產生維數災難的問題。通過訓練模型可有效地建立感知（輸入）與決策（輸出）之間的映射關系。依據此映射關系，USV在每個決策周期選擇Q值最大的動作執行，從而能夠成功避開障礙物并規劃出最優路線。仿真結果表明，在迭代訓練8 000次時，平均損失函數能夠較好地收斂，這證明USV有效學習到了如何避開障礙物并規劃出最優路線。該方法是一種不依賴模型的端到端路徑規劃算法。

關鍵詞：水面無人艇（USV）; 自主避障; 路徑規劃; 深度Q網絡; 卷積神經網絡; 強化學習

中圖分類號：? U675.73

文獻標志碼：A

Path planning algorithm for unmanned surface vessels

based on deep Q network

SUI Bowen， HUANG Zhijian， JIANG Baoxiang， ZHENG Huan， WEN Jiayi

（Merchant Marine College， Shanghai Maritime University， Shanghai 201306， China）

Abstract：

In order to realize the autonomous obstacle avoidance navigation of unmanned surface vessels （USVs） in unknown environment， a USV obstacle avoidance path planning algorithm based on the deep Q network is proposed. In this algorithm， the deep learning is applied to the Q-learning algorithm， and the Q function is estimated by the deep neural network， which effectively solves the problem of dimension disasters in the path planning of complex waters environment caused by the traditional Q-learning algorithm. The mapping relationship between the perception （input） and the decision （output） can be established effectively by the trained model. According to the mapping relationship， a USV chooses the action? with the largest Q value in each decision cycle， so that it can successfully avoid obstacles and plan the optimal route. The simulation results show that， the average loss function can converge well through the iteration training of 8 000 times， which proves that the USV has learned how to avoid obstacles and plan the optimal route effectively. This method is an end-to-end path planning algorithm which does not depend on models.

Key words：

unmanned surface vessel （USV）; autonomous obstacle avoidance; path planning;

deep Q network; convolutional neural network; reinforcement learning

0 引 言

水面無人艇（unmanned surface vessel， USV）在復雜水域環境中要具備自主航行和避障能力，首先面對的是避障路徑規劃問題，即如何規劃出一條從出發點到目標點的安全且最優的航線。目前，根據智能化程度，研究與應用較多的USV路徑規劃算法包括傳統算法、啟發式算法、智能算法、強化學習算法等4類[1]。

傳統算法如可視圖法[2]、人工勢場法[3]等缺乏靈活性，易于陷入局部最優值。啟發式算法是相對于最優化算法提出的，是一種搜索式算法，在離散路徑拓撲結構中得到了很好的應用[4]。智能算法是人們在仿生學研究中發現的算法，常用的智能算法包括遺傳算法、神經網絡算法和群智能算法[1]。以上3類算法都是基于樣本的監督學習算法，即算法需要完備的環境信息。因此，在未知環境（即系統中沒有新環境的先驗信息）水域采用這3種算法USV很難有效地進行路徑規劃。

強化學習算法是由美國學者MINSKY于1954年提出的。目前常用的強化學習算法主要包括Q學習、SARSA學習、TD學習和自適應動態規劃算法等。該類算法通過智能體與環境進行大量的交互，經過不斷試錯獲取未知環境的信息反饋，從而優化路徑規劃策略。該類學習算法不依賴模型和環境的先驗信息，是一種自主學習和在線學習算法，具有較強的不確定環境自適應能力，可以借助相應傳感器感知障礙物信息進行實時在線路徑規劃。例如，王程博等[5]提出了一種基于

Q學習的無人駕駛船舶路徑規劃方法，將強化學習創新應用至無人駕駛船舶的路徑規劃領域，利用強化學習具有自主決策的特點來選擇策略最終完成無人駕駛船的自主避障和路徑規劃。然而，傳統的Q學習是以Q值表的形式存儲狀態行為信息的，而在復雜水域環境中Q值表存儲不了大量的狀態行為信息從而會導致維數災難問題。

為解決維度災難問題并使USV在未知環境水域具有較高的自適應性和穩定性，本文基于深度Q網絡提出一種端對端的USV路徑規劃算法。該算法將深度學習與Q學習相互融合，以神經網絡輸出代替Q值矩陣，有效解決了維度災難問題。該算法是一種無模型的端到端的路徑規劃算法，即通過深度學習實時感知高維度障礙物信息，然后根據感知到的環境信息作出決策，通過端到端的訓練環境信息輸入和規劃路徑輸出，減少了大量中間環節的運算，有效提高了算法的自適應性和模型泛化能力。此外，由于該算法是一種不依賴模型的端到端的路徑規劃算法，所以基于該算法的USV智能系統通過實時與環境交互獲取環境信息，并根據獲取的交互數據不斷學習和改善自身決策行為，最終獲得最優策略，規劃出最優路線。相比于傳統路徑規劃算法，本文所提出的路徑規劃算法更具通用性。

1 Q學習算法

Q學習算法最初是由WATKINS等[6]提出的一種無模型的值函數強化學習算法。該算法通過構建一個Q值表儲存狀態動作值，通過智能體與環境的不斷交互獲得獎勵值，進而更新Q值表，更改動作策略集，最終使智能體趨于最優動作集。算法原理圖見圖1。

在Q學習算法中，USV根據當前的狀態選擇一個動作對環境造成影響，并收到環境給出的反饋（正反饋或負反饋），根據反饋信號作出下一步決策，原則是使得環境的正反饋概率最大[7]。例如，USV路徑規劃決策系統在t時刻選擇動作at，環境接收動作后由狀態st轉移到下一個狀態st+1，狀態轉移概率P取決于at和st：

根據未來獎勵對當前獎勵長期影響的觀點選擇最優動作，在策略π的作用下，狀態值函數被定義為

式中：Rt（a）為當前狀態下采取行動的即時獎勵;γ∈[0，1]為折扣因子，表示未來獎勵對當前獎勵的重要程度。學習的最終目的就是找到最優策略π*，使得每個狀態的值函數取得最大值。

定義狀態動作值函數Q：

式中，Q*（s，a）表示在狀態s下采取動作a所得的最大累積獎勵值;s0和a0分別為初始狀態和在初始狀態下執行的動作。基于當前的狀態和動作，在最優策略π*的作用下，系統將以概率P（s，a，st）轉移到下一狀態st，則由式（4）可得Q學習算法的基本形式：

由式（3）進一步可得最優策略的狀態動作表達式：

式（6）表明，在路徑規劃時只需求得當前的狀態動作值函數Q（s，a），通過不斷對上一狀態的值函數進行迭代更新，即可規劃出全局最優策略。其迭代公式為

式中：α為學習率，主要用于迭代公式的收斂。

2 避障路徑規劃算法

2.1 算法模型結構

本文結合卷積

神經網絡[8]和強化學習提出一種深度強化學習（深度Q網絡）路徑規劃算法。該算法可實現從感知（輸入）到決策（輸出）的端到端的策略選擇。輸入圖片像素后，經過卷積神經網絡對環境信息的逐層提取和對高維特征的感知，從動作空間選取Q值最大的動作執行，從而得到平均獎勵最大的策略即為最優策略，實現對USV的端到端的自主避障控制和路徑規劃。本文提出的路徑規劃算法結構見圖2。

首先根據馬爾科夫決策過程模型[9]和Bellman方程[10]得到當前狀態的動作值函數：

式中：st+1為下一狀態;at+1為下一狀態最優動作;R為采取下一狀態的獎勵。通過多次實驗可找到最優Q*（s，a）：

在狀態s下通過多次實驗可得到多個Q值，當實驗次數足夠多時，該期望值就無限接近真實的Q值。因此，可以通過神經網絡估計Q值：

式中，θ是神經網絡的參數。

利用式（10）估計Q值的方法會產生一定的誤差，因此引入損失函數來反映利用神經網絡估計的Q值與真實Q值之間的差：

采用隨機梯度下降方式不斷優化網絡參數，使損失函數盡可能降到最低，即估計的Q值盡可能逼近真實值，使得智能體每次都能選取最優的Q值從而進行最優決策。

2.2 動作空間設計

在仿真過程中對USV和仿真環境進行簡化處理：把USV近似為1×1像素大小的像素塊，定義USV的動作空間

包括上、下、左、右4個基本動作，并采用ε貪婪策略，分別以ε的概率進行隨機動作選擇來探索新環境，以1-ε的概率選擇Q值最大的動作a。本文設置的探索-利用機制如下：

采用ε貪婪策略，既可以保證USV在策略選擇時選取較優策略，又能保證所有狀態空間都能被探索到。

2.3 激勵函數的設計

本實驗中動作空間是有限且離散化的，故可將激勵函數R做泛化處理：當USV到達目的地時，獎勵值設為100;當USV與黑色方塊重合時，即表示USV沒有進行有效的避碰，獎勵值設為-100，以示懲罰;其他白色可通行區域所有狀態的獎勵值均設為0，激勵函數的表達式如下：

R=100 （到達目的地）0 （未碰撞，未到達）-100 （發生碰撞）

2.4 深度Q網絡結構

本文采用的卷積神經網絡結構包括2個卷積層和2個全連接層，卷積神經網絡訓練參數設置見表1。

在卷積神經網絡中輸入像素為25×25×3的仿真地圖，見圖3。首先經過卷積核數量為10、大小為2×2的第一個卷積層，提取高維特征，生成25×25×10的特征圖;將第一個卷積層的輸出作為第二個卷積層的輸入，其中第二個卷積層的卷積核數量為20、大小同樣為2×2;將第二個卷積層的輸出作為第一個全連接層的輸入，通過重塑數據形狀，將特征圖轉化為1×12 500的特征向量，再輸入到第二個全連接層，輸出一個1×4的矩陣，分別對應USV的上、下、左、右4個離散動作，最后根據每個數據點的Q值的大小選出最優動作。

3 仿真與實驗

3.1 建立仿真環境

基于Python及相應工具包構建如圖4所示的二維仿真環境。隨機生成625張像素為25×25的圖片，每個像素塊都代表環境的一個狀態，并且在像素為25×25的圖片中隨機生成位置各不相同的1×1像素的黑色方塊代表障礙物，白色區域為可自由通行區域。隨機變換障礙物位置200次，即生成了200×625張圖片作為訓練數據進行訓練。從12 500張圖片中隨機選取4張作為仿真環境，如圖4所示。圖4中左上角、右下角灰色方塊分別代表無人艇的出發點和目標點。

結合仿真環境建立二維直角坐標系，如圖5

所示：A點為USV的出發點，坐標為（1，1）;B點為目標點，坐標為（25，25）。本文中所有仿真環境的出發點和目標點均與圖5保持一致。對于USV來說，這些環境信息都是未知的。

3.2 實驗結果分析

實驗環境配置：CPU為intel i7-7700 4.2 GHz，內存為16 GB，顯卡為英偉達GTX1080 Ti，操作系統Ubuntu 16.04。實驗中采用的訓練數據來自隨機生成的12 500張像素為25×25的圖片。利用同樣的方法隨機生成具有不同障礙物分布的20張圖片作為測試集進行測試。

為簡化仿真實驗復雜度，仿真實驗僅在模擬的水上障礙物靜態環境中進行，在實驗前期USV在不同的時間步與障礙物發生碰撞，環境給出懲罰，以降低下次出現相似狀況的概率，有效指引USV選擇最優策略。在上述4種仿真環境中的路徑規劃效果見圖6。

在訓練開始時，USV會多次與障礙物發生碰撞且規劃路徑波動較大;在訓練3 000次時，算法逐漸規劃出安全路徑，但此時路徑并非最短，所耗費時間也較長;在訓練5 000次時，系統可以有效避開障礙物，算法趨于平穩并逐漸規劃出有效路徑，所需時間也明顯縮短;當訓練8 000次時，系統可以高效避開障礙物并規劃出最優路徑。表2為在上述4種仿真環境中分別訓練不同次數產生的數據平均值。

從訓練數據中隨機選出一批圖片進行訓練，其權值更新取決于損失函數，隨著訓練次數的增加，

式（11）的max Q（st+1，at+1s，a）對應上、下、左、右4個動作中的Q值的最大值。首先將神經網絡預測的Q值存儲起來。經過一段時間的訓練，更新Q值并存儲在與訓練模型相同的文本文件中。新Q值又可以用來訓練模型。重復幾個步驟，直到算法學習到所需的特性。當訓練開始時，神經網絡估計的Q值與真實Q值的差值較大，此時的損失函數波動加大（見圖7），顯然此時算法還沒有學會如何避開障礙物。

隨著訓練次數的增加，算法逐漸學會捕捉相應的特性，當訓練結束時算法的平均損失已經明顯收斂（見圖8），這表明網絡誤差較小，USV已經很好地學會如何避開障礙物規劃安全航線。

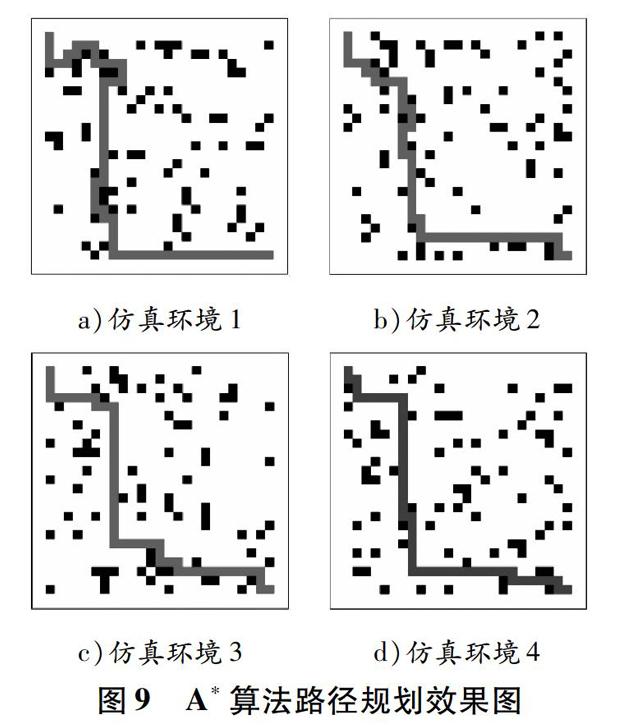
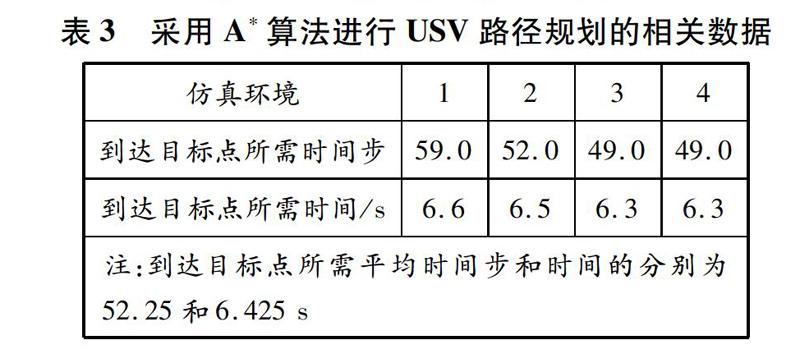
針對上文的4種仿真環境，采用A*算法對USV進行路徑規劃，如圖9所示：隨著仿真環境的變化，A*算法并不穩定，在仿真環境1和仿真環境2中，USV的路徑規劃均存在繞遠現象，并不是最優路線，沒有實現高效合理的路徑規劃目標。采用A*算法進行路徑規劃的相關數據見表3。

由表2和表3可知：采用深度Q網絡進行USV路徑規劃時，當迭代8 000次時算法已經收斂，從出發點到目標點所需平均時間步和時間分別為49.0和5.3 s;采用A*算法進行USV路徑規劃時，從出發點到目標點所需平均時間步和時間分別為52.25和6.425 s。由此可知，采用深度Q網絡進行USV路徑規劃比采用傳統的A*算法更加高效。

以上仿真結果表明，本文提出的路徑規劃算法可以實現USV航行的全局路徑規劃，并且比傳統的A*算法更加高效，可以有效地避開環境中的障礙物并規劃出最優航線。

4 結束語

本文基于深度Q網絡提出一種無須模型的端到端的無人艇（USV）路徑規劃算法。該算法以神經網絡的輸出代替Q值矩陣，解決了采用傳統Q學習進行路徑規劃時的維數災難問題。采取經驗回放機制，有利于提高USV的學習效率，提高USV到達目標的速度。該算法無須知道環境先驗信息，能夠通過與環境的交互獲取數據并進行在線學習，相比于傳統的基于模型的路徑規劃算法，本文所提出的路徑規劃算法更具通用性。通過仿真可知：USV在與環境交互初期，對環境信息了解較少，會發生碰撞及路徑規劃波動較大等現象;隨著迭代次數的增加，USV的決策系統累積學習經驗，提高對環境的自適應性，最終成功規劃路徑并安全抵達目標點。通過對比實驗可知，基于深度Q網絡的USV路徑規劃算法比傳統的A*算法更加高效合理。然而，本文對USV的動作空間進行了離散化處理，與真實情況尚有差距，針對USV的連續動作空間進行路徑規劃將是今后的研究方向。

參考文獻：

[1]劉志榮， 姜樹海. 基于強化學習的移動機器人路徑規劃研究綜述[J]. 制造業自動化， 2019， 41（3）： 90-92.

[2]李洪偉， 袁斯華. 基于Quartus Ⅱ的FPGA/CPLD設計[M]. 北京： 電子工業出版社， 2006.

[3]陳超， 耿沛文， 張新慈. 基于改進人工勢場法的水面無人艇路徑規劃研究[J]. 船舶工程， 2015（9）： 72-75.

[4]邱育紅. GIS空間分析中兩種改進的路徑規劃算法[J]. 計算機系統應用， 2007， 16（7）： 33-35.

[5]王程博， 張新宇， 鄒志強， 等. 基于Q-learning的無人駕駛船舶路徑規劃[J].船海工程， 2018， 47（5）： 168-171.

[6]WATKINS C J C H， DAYAN P. Q-Learning[J]. Machine Learning， 1992， 8（3/4）： 279-292.

[7]衛玉梁， 靳伍銀. 基于神經網絡的Q-learning算法的智能車路徑規劃[J].火力與指揮控制， 2019， 44（2）： 46-49.

[8]林景棟， 吳欣怡， 柴毅， 等. 卷積神經網絡結構優化綜述[J].自動化學報， 2018（2）： 75-89.

[9]劉成勇， 萬偉強， 陳蜀喆， 等. 基于灰色馬爾科夫模型的船舶交通流預測[J]. 中國航海， 2018， 41（3）： 95-100.

[10]李金娜， 尹子軒. 基于非策略Q-學習的網絡控制系統最優跟蹤控制[J]. 控制與決策， 2019（4）： 17-25.

（編輯 趙勉）

收稿日期： 2019-08-26

修回日期： 2019-09-29

基金項目：

國家自然科學基金（61403250）

作者簡介：

隨博文（1992—），男，河南商丘人，碩士研究生，研究方向為深度強化學習，（E-mail）201410121215@stu.shmtu.edu.cn;

黃志堅（1979—），男，江西九江人，高級工程師，研究方向為控制算法，（E-mail）zjhuang@shmtu.edu.cn