具有橫傾抑制功能的船舶PID微分補償航向控制

孫武臣　卜仁祥　劉勇

摘要：為改善船舶航向自動舵性能和減小船舶轉向時的橫傾幅度，提出一種基于模糊邏輯控制和滑模PID微分補償的船舶航向保持控制策略。分析PID控制的積分超調問題和船舶轉向時的橫傾特點。對PID控制進行滑模變形，并引入微分項對PID控制的積分項進行補償以消除積分超調。以橫傾角和橫傾角速度為輸入設計模糊控制規則，對滑模PID微分補償控制器參數進行調節以減小轉向時橫傾角。以集裝箱船“MV KOTA SEGAR”MMG模型為控制對象進行MATLAB仿真。仿真結果表明：該控制器能夠減小船舶轉向時的橫傾幅度，最大橫傾抑制率可達71%;解決了PID控制的積分超調問題，具有參數易調節等特點。

關鍵詞：航向保持控制; 橫傾抑制; PID微分補償; 模糊邏輯控制

中圖分類號：? U664.82

文獻標志碼：A

Ship course control with heel inhibition capacity

based on PID differential compensation

SUN Wuchen， BU Renxiang， LIU Yong

（Navigation College， Dalian Maritime University， Dalian 116026， Liaoning， China）

Abstract：

In order to improve the ship course autopilot performance and reduce the heel amplitude during ship steering， a ship course keeping control strategy based on the fuzzy logic control and the sliding mode PID differential compensation is proposed. The integral overshoot problem of PID control and the heel feature when ship steering are analyzed. PID control is deformed by the sliding mode， and the differential term is introduced to compensate the integral term of PID control to eliminate the integral overshoot. A fuzzy control rule is designed with the heel angle and the angular velocity of heel as the input， and the parameters of the sliding mode PID differential compensation controller are adjusted to reduce the heel angle during ship steering. The MMG model of the container ship “MV KOTA SEGAR” is used as the control object for MATLAB simulation. The simulation results show that： the controller can reduce the heel amplitude during ship steering， and the maximum heel inhibition rate can reach 71%; the integral overshoot problem of PID control is solved， and the parameters are easy to adjust.

Key words：

course keeping control; heel inhibition; PID differential compensation; fuzzy logic control

0 引 言

自20世紀20年代初陀螺羅經研制工作取得實質性進展后，船舶航向保持控制一直是船舶運動控制領域的重要研究課題[1]。最初的航向控制器只是簡單的比例控制，且只能用于低精度要求的航向保持控制，但它讓人們看到了在船舶操縱領域實現自動控制的希望。后來隨著伺服系統理論和電子器件的發展，出現了PID自動舵。PID自動舵具有結構簡單可靠、控制參數少等優點，因此目前大多數船舶仍裝備這種舵。由于PID自動舵的設計基于精確數學模型，而船舶運動模型隨速度、水深、載荷狀態和外部環境干擾的變化而變化，所以常規PID自動舵很難保證在所有的情況下都具有滿意的控制效果[2]。為解決上述問題，在20世紀60年代末瑞典等國家的學者將自適應技術應用于船舶航向保持控制，提高了自動舵在各種氣候條件下適用的可能性[3-4]。然而自適應方法以參數估算或模型試驗為基礎，建立精確的船舶運動數學模型是困難的，只有經驗豐富的舵手才能很好地控制船舶。自20世紀80年代以來，人們開始尋求類似于人工轉向的智能控制技術，各種新型控制算法被應用于航向自動舵，如：TZENG[5]將船舶轉向過程控制轉化為采用順序梯度恢復算法（sequential gradient-restoration algorithm）解決的BOLZA最優控制問題，實現了從設定航向到期望航向的平穩過渡，并可在航向響應速度與超調量之間進行權衡;劉勝等[6]運用飽和局部分析法，將不確定非線性船舶動力模型轉化為線性微分包含模型，設計了飽和線性反饋控制律，設計的控制器具有工程實現容易、轉向平穩快速和無超調等特點;張顯庫等[7]利用閉環增益成形算法設計對模型攝動和風浪干擾具有一定魯棒性的PID控制器，改進了設計分區前饋控制器，提高了轉向時的響應速度、系統靈敏度和系統控制質量;甘浪雄等[8]設計了航向成形算法對船舶轉向過程進行前饋調節，并改進模糊PID控制器，提高了控制的動態性能和穩態精度等。

然而，現有的航向控制器主要針對航向保持和轉向過程進行控制，很少考慮船舶轉向過程中的橫傾問題。船舶轉向尤其大角度轉向必然產生橫傾，過度的橫傾不僅嚴重威脅船舶航行安全，而且對船舶適航性、貨物綁扎固定、船員舒適性有很大的影響[9]，對滾裝船、客滾船、集裝箱船、豪華郵輪等重心較高的船舶的影響更甚。

本文針對傳統PID控制參數不易調節、積分超調問題，對傳統PID控制進行滑模變形，不再是單獨對航向偏差積分，而是對航向偏差和偏差變化率同時積分;為減小船舶轉向時的橫傾幅度，根據船舶轉向時橫傾角大小及其變化率，設計模糊控制規則，對控制器參數進行調節。利用MATLAB仿真環境進行驗證，建立了集裝箱船“MV KOTA SEGAR”MMG模型并加入了風干擾和舵機模型，以更接近實際情況。

1 基本描述

1.1 船舶操縱運動方程

描述船舶的操縱運動時，通常采用兩種不同的坐標系：一種是慣性（固定）坐

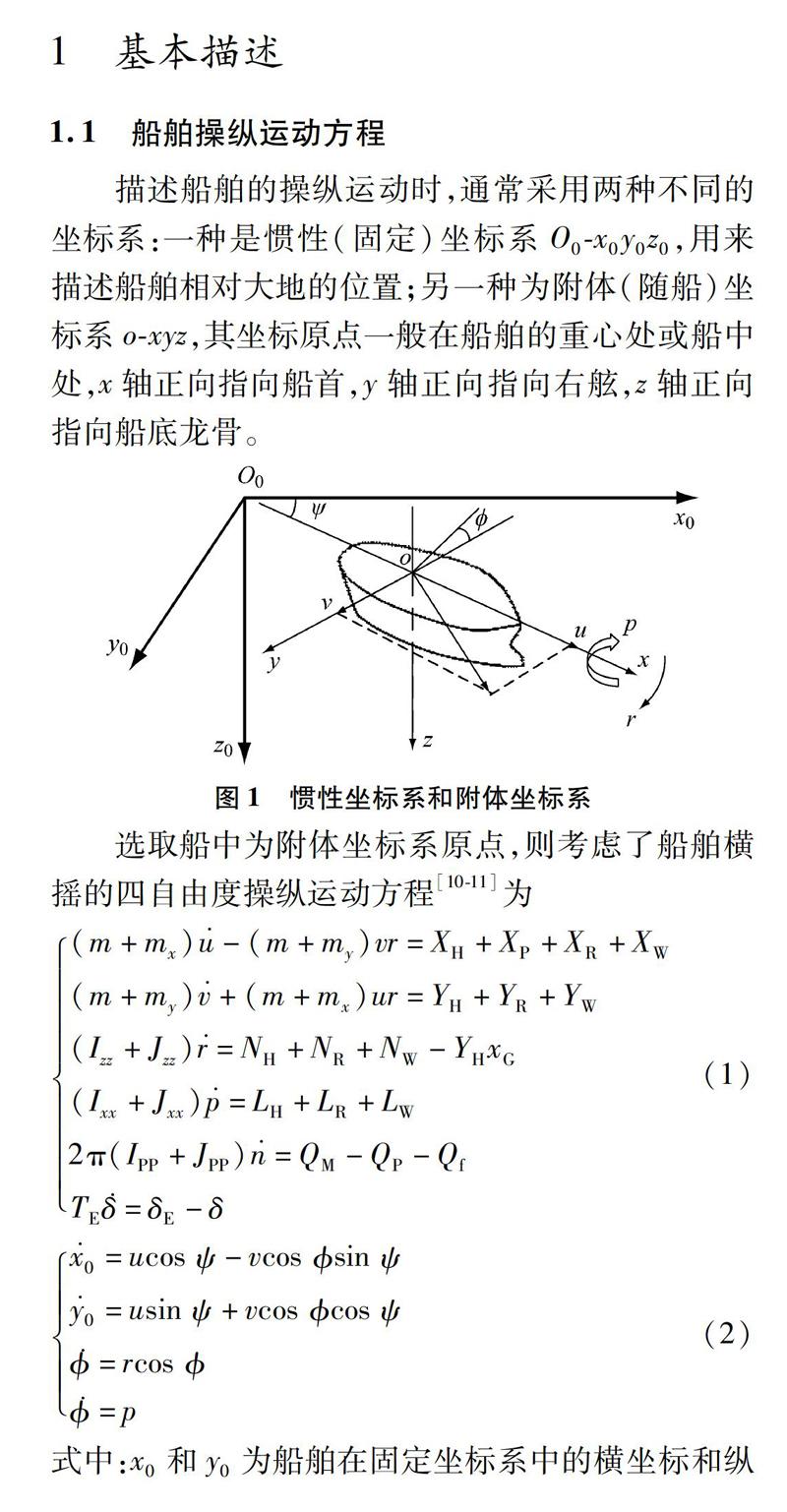
標系O0-x0y0z0，用來描述船舶相對大地的位置;另一種為附體（隨船）坐標系o-xyz，其坐標原點一般在船舶的重心處或船中處，x軸正向指向船首，y軸正向指向右舷，z軸正向指向船底龍骨。

選取船中為附體坐標系原點，則考慮了船舶橫搖的四自由度操縱運動方程[10-11]為

式中：x0和y0為船舶在固定坐標系中的橫坐標和縱坐標;u和v分別為船舶在附體坐標系中的縱向速度和橫向速度;ψ和r分別為艏向角和轉艏角速度;和p分別為橫傾角和橫傾角速度;n、δE和δ分別為主機轉速、命令舵角和實際舵角;TE為舵機時間常數，一般取2.5～3 s;m、mx和my分別為船舶的質量、縱向附加質量和橫向附加質量;Izz和Jzz分別為船舶的轉動慣量和附加轉動慣量;X和Y分別為作用于船體縱向和橫向的力;N和L分別為繞垂直軸和縱軸的力矩;下標H、P、R和W分別表示流體黏性、螺旋槳、舵葉和外界干擾;xG為船舶重心在附體坐標系中x方向上的坐標;Ixx和Jxx分別為船舶的橫搖慣性矩和附加轉動慣量;IPP和JPP分別為螺旋槳與軸系的轉動慣量和附加轉動慣量;QM、QP和Qf分別為主機產生的轉矩、螺旋槳吸收的轉矩和軸系摩擦消耗的轉矩。

1.2 控制目標

控制目標為確定舵角δ，使船舶保持期望航向航行，即航向偏差ψe→0，且轉向時船舶具有橫傾抑制功能。

2 控制器設計

2.1 PID微分補償控制設計

PID控制率的基本形式為

由于PID控制器的3個參

數kp、ki和kd之間相互影響，調整其中一個參數，可能會影響另外兩個參數的性能，所以對式（3）的形式稍作變形，可得到

觀察式（5）可知，PID控制的3個參數轉化為k1、k2和kd，參數的物理意義變得更為明顯，有利于參數的調節和優化[12-13]。為方便書寫，kd用k3代替。

為消除積分超調問題，在式（5）的積分項中添加微分項進行補償，可得

由式（7）可知，控制器的參數仍為3個，但在系統輸出趨近于穩定（即ψe>0，而e<0;或ψe<0，而e>0）時能夠抵消積分項對系統輸出偏差的積分，而在系統偏差偏離控制目標（即ψe<0，而e<0;或ψe>0，而e>0）時積分項會加速系統穩定。

2.2 模糊橫傾抑制設計

根據船舶轉向時橫傾變化特點[14-15]，以橫傾

角和橫傾角速度p為輸入，Δk3為輸出設計模糊控制規則，對PID微分補償控制器參數進行調節以達到抑制橫傾的目的。

對橫傾角、橫傾角速度p和輸出Δk3的模糊集和論域定義如下：、p和Δk3的模糊集均取為{NB， NM， NS， ZO， PS， PM， PB}，其中NB、NM、NS、ZO、PS、PM和PB分別表示負大、負中、負小、零、正小、正中和正大;的論域為{-6， -5， -4， 0， 4， 5， 6};p的論域為{-0.5， -0.4， -0.3， 0， 0.3， 0.4， 0.5};Δk3的論域為{-18， -12， -6， 0， 6， 12， 18}。論域可根據需要自行設計，上面的數

據是以“MV KOTA SEGAR”MMG模型為被控對象設計的。隸屬度函數選用三角形隸屬度函數和S形隸屬度函數。通過仿真，由橫傾角和橫傾角速度p變化趨勢設計減小橫傾的模糊控制規則，根據49條模糊規則（見表1）建立模糊控制表。系統的輸入、輸出隸屬度函數見圖2～4。數值計算采用MAMDANI的Min模糊蘊含關系[16]、ZADEH的Max-min推理合成、最大隸屬度平均法（mom）去模糊化[17]等算法。

2.3 控制器工作原理示意圖

具有橫傾抑制功能的PID微分補償控制器工作原理示意圖見圖5。

3 仿真驗證與分析

為驗證控制策略的可行性和控制效果，本文以集裝箱船“MV KOTA SEGAR”為仿真對象，對不同情況下的橫傾和航向變化進行仿真和對比分析。船型主要參數：垂線間長217 m;型寬37.3 m;型深15.693 m;吃水12.5 m;排水量67 867.2 t;螺旋槳直徑7.9 m;舵葉面積48.8 m2。控制器參數：k1=0.004 6;k2=0.028; k3=18;k=0.033。

3.1 仿真1

設定初始航速19.4 kn、風向30°、風速10 m/s，恒定風的影響用風壓差角表示[18]，浪和隨機風的影響采用白噪聲驅動的二階振蕩環節H（s）=0.419 8s/（s2+0.363 8s+0.367 5）表示[19-20]，初始航向偏差為60°，PID微分補償控制器與常規PID控制器結果對比見圖6。

由圖6可知，常規PID控制器下航向曲線存在4°左右超調。產生超調的根本原因是積分項的存在：在航向趨于穩定的過程中，積分項積累了不利信息（A區），而在航向偏差偏離目標時積分反應又過于遲鈍;根據積分性質，必然產生反向積分區域（B區），而且只有B區面積等于A區面積，才能使航向偏差最終趨于零。PID微分補償控制器下的航向曲線不存在超調，且航向穩定時間比常規PID控制器下的明顯縮短，這是由于控制器中的微分補償項在航向趨于穩定的過程中抵消了積分項對偏差的積分，而在航向偏離目標時加快了積分項的反應速度，抑制航向繼續偏離目標，從而加快系統穩定。

3.2 仿真2

在船舶轉向操縱過程中，由于艏搖與橫搖之間相互耦合，所以橫傾不可避免。小橫傾角對船舶航行安全影響不大，但過大的橫傾角嚴重威脅船舶航行安全，甚至會導致船舶傾覆。因此，設計的控制器應該對小橫傾角不敏感，對越大的橫傾角，橫傾抑制能力越強。利用不同初穩心高度（GM）條件下船舶轉向時橫傾角不同，設計仿真實驗對控制器這種性能進行驗證。設定GM分別為0.6 m、0.9 m，初始航向偏差為60°，橫傾抑制效果分別見圖7和8。由圖7和8可知：當GM為0.6 m時，在橫傾抑制作用下最大橫傾角由9.5°減為3.3°，橫傾抑制率為65%;當GM為0.9 m時，在橫傾抑制作用下最大橫傾角由6.3°減為3.2°，橫傾抑制率為49%。GM為0.6 m時的橫傾抑制效果明顯優于GM為0.9 m時的橫傾抑制效果，驗證了該控制器橫傾角越大，橫傾抑制效果越好的特點。

3.3 仿真3

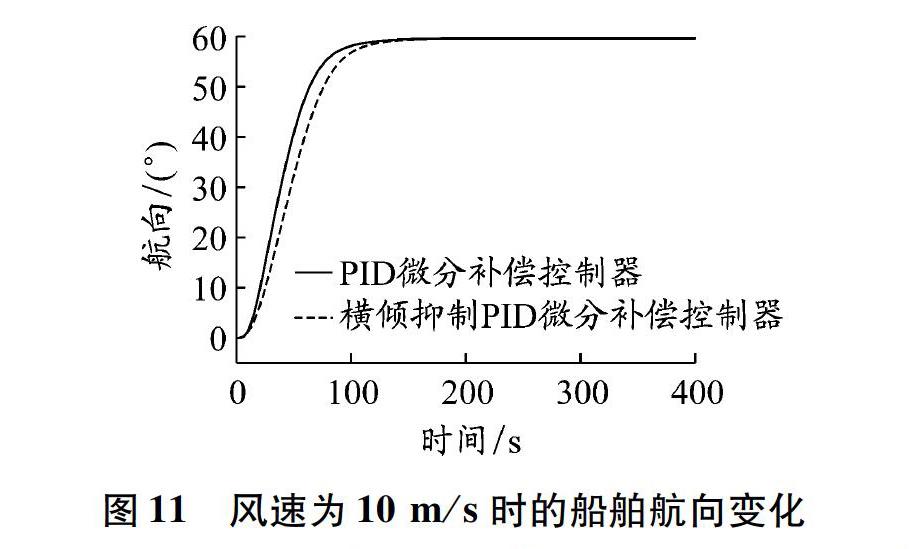
設定風速分別為10 m/s和18 m/s，其他干擾條件同仿真1，GM為 0.6 m，初始航向偏差為60°。不同風速條件下的橫傾抑制效果見圖9和10，風速為10 m/s時的船舶航向變化見圖11。

由圖9和10可知：當風速為10 m/s時，最大橫傾角在橫傾抑制作用下由13.4°減為5.6°，橫傾抑制率為58%;當風速為18 m/s時，最大橫傾角在橫傾抑制作用下由20.8°減為10.9°，橫傾抑制率為48%。與圖7對比可知，風干擾使船舶轉向時橫傾角增大，且航向保持時船舶具有穩定橫傾，可見該控制器對穩定橫傾不起作用，這是因為：用于橫傾抑制功能的模糊控制規則是以橫傾角和橫傾角速度為輸入而設計的，當船舶處于穩定橫傾狀態時，橫傾角速度為零，按照模糊控制規則此時對應的輸出為零，對PID微分補償控制器參數沒有影響，即此時控制器不具有橫傾抑制功能。這種設計符合航海實際情況，船舶在風力作用下所產生的穩定橫傾不宜通過舵角來調整，因為用舵角調整不僅會增加舵機燃油消耗，而且會給控制器的航向保持功能帶來不確定影響。實船上一般通過壓載水系統調節穩定橫傾，這不是本文研究內容，暫不詳細介紹。由圖11可以看出，在具有橫傾抑制功能的PID微分補償控制器作用下的航向響應速度略慢，因此在設計具有橫傾抑制功能的控制器時需充分考慮實際情況，避免因不必要的加強橫傾抑制功能而減慢航向響應速度。

3.4 仿真4

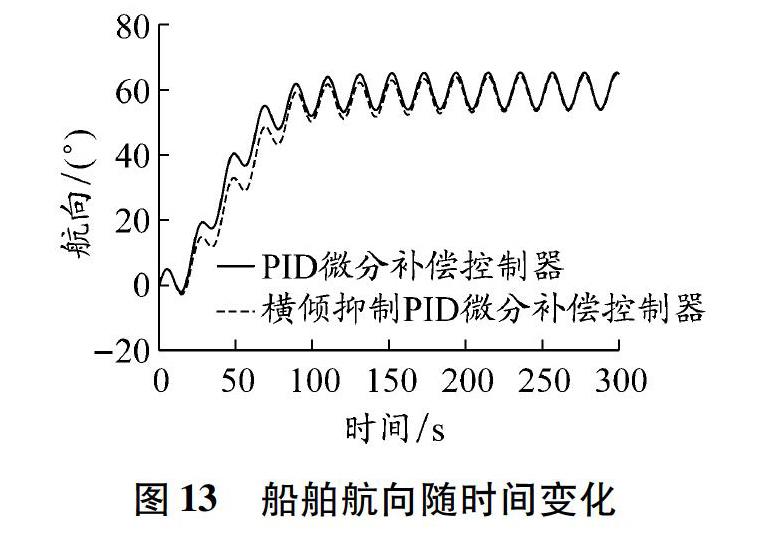
設計具有橫傾抑制功能的控制器的目的是為了減小船舶轉向時的橫傾幅度，同時不影響船舶的航向保持功能。為驗證控制器的這種性能，設定GM為0.6 m，初始航向偏差為60°，船首向受幅值為5°的正弦信號干擾進行仿真。其橫傾抑制效果見圖12，船舶航向變化見圖13。

觀察仿真結果可知：（1）在船舶轉向開始時，控制器具有很好的橫傾抑制效果，最大橫傾抑制率可達71%;與PID微分補償控制器相比，在橫傾抑制PID微分補償控制器下船舶航向響應速度略慢，再次驗證了仿真圖10得到的結論。（2）在船舶進入航向保持階段后，在正弦信號干擾下，橫傾抑制PID微分補償控制器能夠很好地跟蹤控制目標，且具有一定的橫傾抑制功能。仿真結果驗證了該控制器能夠減小船舶轉向時的橫傾幅度，防止轉向時橫傾過大，控制器的橫傾抑制功能不會影響船舶的航向保持功能，實現了控制器設計的目的。

4 結 論

本文對船舶航向PID控制率進行了滑模變形，并引入了微分項對PID控制中的積分項進行補償;根據船舶轉向時的橫傾特點設計了模糊邏輯規則，用以調節PID微分補償控制器的參數，使控制器能夠減小船舶轉向時的橫傾幅度，具有橫傾抑制功能。采用集裝箱船“MV KOTA SEGAR”MMG模型進行仿真，結果驗證了本文所設計的控制器能夠消除常規PID控制器的積分超調問題，在船舶轉向時具有橫傾抑制功能，橫傾角越大橫傾抑制效果越好，最大橫傾抑制率可達71%，且不影響船舶航向保持性能，符合航海實際需求。為提高控制器的魯棒性，下一步的工作是將控制器與其它智能控制技術相結合，對控制器參數進行在線優化。

參考文獻：

[1]徐國平， 張顯庫. 船舶自動舵研究綜述[J]. 中國造船， 2013， 54（2）： 191-200.

[2]張顯庫. 船舶控制系統[M]. 大連： 大連海事大學出版社， 2010： 4-7.

[3]賈欣樂， 張顯庫. 船舶運動智能控制與H∞魯棒控制[M]. 大連： 大連海事大學出版社， 2002： 9-13.

[4]HASELTALAB A， NEGENBORN R R. Adaptive control for autonomous ships with uncertain model and unknown propeller dynamics[J]. Control Engineering Practice， 2019， 91： 1-12.

[5]TZENG C Y. Optimal control of a ship for a course-changing maneuver[J]. Journal of Optimization Theory and Applications， 1998， 97： 281-297. DOI： 10.1023/A：1022674516570.

[6]劉勝， 周麗明. 船舶轉向靜態飽和控制器設計[J]. 系統仿真學報， 2009， 21（7）： 1983-1985. DOI： 10.16182/j.cnki.joss.2009.07.072.

[7]張顯庫， 趙翔宇. 船舶轉向的魯棒控制及其優化設計[J]. 哈爾濱工程大學學報， 2006， 27（3）： 319-322.

[8]甘浪雄， 鄧巍， 周春輝， 等. 船舶航向模糊控制器優化設計及仿真[J]. 武漢理工大學學報（交通科學與工程版）， 2019， 43（3）： 398-403. DOI： 10.3963/j.issn.2095-3844.2019.03.005.

[9]LIANG Lihua， WEN Yu. Rudder roll stabilization with disturbance compensation model predictive control[J]. Journal of Marine Science and Technology， 2019， 24： 249-259. DOI： 10.1007/s00773-018-0550-6.

[10]賈欣樂， 楊鹽生. 船舶運動數學模型： 機理建模與辨識建模[M]. 大連： 大連海事大學出版社， 1999： 170-173.

[11]YO Fukui， HIROTAKE Yokota， HIROYUKI Yano， et al. 4-DOF mathematical model for manoeuvring simulation including roll motion[J]. Journal of Marine Science and Technology， 2016， 24： 167-179. DOI： 10.2534/jjasnaoe.24.167.

[12]卜仁祥. 欠驅動水面船舶非線性反饋控制研究[D]. 大連： 大連海事大學， 2007.

[13]朱業求. 船舶航向PID控制參數優化研究[D]. 大連： 大連海事大學， 2012.

[14]HIRANO M， TAKASHINA J. A calculation of ship turning motion taking coupling effect due to heel into consideration[J]. Transactions of the West-Japan Society of Naval Architects， 1980， 59： 71-81.

[15]王立軍. 船舶大舵角轉向時艏搖與橫搖的耦合仿真研究[J]. 船舶與海洋工程， 2013（1）： 6-11.

[16]MAMDANI E H， ASSILIAN S. An experiment in linguistic synthesis with a fuzzy controller[J]. Internatinal Journal of Man-Machine Studies， 1975， 7（1）： 1-13. DOI： 10.1016/S0020-7373（75）80002-2.

[17]ZADEH L A. Fuzzy sets[J]. Journal of Information and Control， 1965， 8： 338-353. DOI： 10.1016/S0019-9958（65）90241-X.

[18]SUN Wuchen， BU Renxiang， LIU Yong， et al. Prediction of leeway and drift angle based on empirical formula[C]//2018 Asia-Pacific Conference on Intelligent Medical and 7th Internaltional Conference on Trasportation and Traffic Engineering （APCIM 2018 & ICTTE 2018）. Association for Computing Machinery， 2018： 196-199. DOI： 10.1145/3321619.3321661.

[19]ZHANG Xianku， FENG Yongxiao. Control algorithm of YUPENG ship autopilot based on tangent function nonlinear feedback[J]. Journal of Measurement Science and Instrumentation， 2017， 8（1）： 73-78. DOI： 10.3969/j.issn.1674-8042.2017.01.012.

[20]馮永孝， 張顯庫. 非線性修飾與模糊控制船舶航向保持控制比較[J]. 中國航海， 2018， 41（4）： 12-15， 27.

（編輯 賈裙平）

收稿日期： 2019-11-27

修回日期： 2020-01-03

基金項目：

國家自然科學基金（61751202， 61751205， U1813203）;遼寧省自然科學基金引導計劃（20170540089）;遼寧省自然科學基金計劃重點項目（20170540098）;大連海事大學航海學院2019年一流學科開放研究基金

作者簡介：

孫武臣（1987—），男，河南鹿邑人，碩士研究生，研究方向為船舶運動控制、航海科學與技術，（E-mail）chenwusun@163.com;

卜仁祥（1975—），男，遼寧岫巖人，副教授，博士，研究方向為交通運輸工程、船舶運動控制、航海科學與技術，（E-mail）burenxiang@dlmu.edu.cn