蒙特卡洛與馬爾可夫方法在降水預測中的應用

黃鶴 張維江 李娟

摘 要：為了更深入地分析原州區的降水特征，為該區域水資源預測提供依據，基于原州區1957—2016年60 a降水資料，采用蒙特卡洛方法推求降水分布，采用K-S檢驗對模型進行顯著性檢驗，采用基于歐氏距離的層次聚類方法進行狀態劃分，確定了原州區的降水分布，建立了適用于原州區的滑動平均加權馬爾可夫預測模型。根據已有數據驗證了預測結果的有效性，再結合已確定的降水分布，通過K-S檢驗，檢驗了未來5 a降水預測的準確性。結果表明：原州區降水分布符合P-Ⅲ型分布;馬爾可夫模型適用于原州區降水預測，且未來5 a的降水預測結果是準確的，分別為508.5、520.8、554.9、451.0、466.6 mm。

關鍵詞：蒙特卡洛方法;馬爾可夫模型;隨機模擬;降水預測;原州區;K-S檢驗

中圖分類號：TV11 文獻標志碼：A

doi：10.3969/j.issn.1000-1379.2020.05.004

Abstract： In order to analyze the characteristics of precipitation in YuanzhouDistrict and provide a basis for water resources prediction in the region， based on the precipitation data from 1957 to 2016 of the district， the Monte Carlo method was used to estimate the precipitation distribution and the K-S test was used to model the significant test. It used the hierarchical clustering method based on Euclidean distance to divide the state， determined the precipitation distribution of the region and established a sliding average weighted Markov prediction model which was suitable for Yuanzhou District. Based on the existing data， the true validity of the prediction results was verified. Combined with the determined precipitation distribution， the accuracy of precipitation prediction for the next 5 years was tested by K-S test. Comparing with Pearson three-type distribution， the results show that the precipitation distribution in Yuanzhou District is more consistent with the log-normal distribution. The Markov model can be applied to the precipitation forecast in the region， and the prediction results of the sliding average precipitation in the next 5 years are real and effective， respectively 508.5， 520.8， 554.9， 451.0 and 466.6 mm.

Key words： Monte Carlo method; Markov model; stochastic simulation; precipitation prediction; Yuanzhou District; K-S test

1 引 言

由于客觀世界中的一些現象可能與另一種現象存在著某種相似性，因此我們經常從一種現象出發來研究另一種現象。當某個概率模型可以描述隨機系統并可以基于此概率模型進行實驗時，這種實驗方法即為隨機模擬方法[1]。近年來，隨機模擬在水文系統預測中發展迅速，取得了顯著進展[2]。劉新立[3]研究了隨機過程情況下隨機模擬和馬爾可夫鏈在水災風險管理中所起的作用，研究表明兩者結合可以評估未來若干個時間單位水災所造成的風險;尹正杰等[4]提出了一個同時含有趨勢、季節、隨機3個分量的時間序列模型，并通過此時間序列模型對灌區灌溉需水量進行隨機模擬;溫季等[5]探討了集中作物需水量的隨機模擬及預測模型，結果表明隨機模擬在作物灌溉管理中具有很強的應用性及普適性。

蒙特卡洛方法與馬爾可夫方法在水文系統方面的應用發展十分迅速。ZHANG等[6]研究開發了基于馬爾可夫鏈-蒙特卡洛的多級因子分析方法，從而更好地對水文模型參數不確定性進行評估;KNIGHTON等[7]通過蒙特卡洛方法將建立的概率分布應用于已知模型，用來估計水文模型的不確定性;劉悅憶等[8]在淮河流域水動力學-水質模型的基礎上，使用蒙特卡洛方法隨機模擬了大量入流數據并將其用作模型的輸入條件進行計算，建立了基于蒙特卡洛模擬的水質概率預報模型;李娟等[9]應用滑動平均-馬爾可夫模型對固原市隆德縣的降水進行預測，研究證明改進后的馬爾可夫模型預測精度較高;王艷等[10]在傳統的馬爾可夫方法上用最優分割法優化了分級標準;岳遙等[11]提出了一種基于投影距離的處理級別特征值的方法來代替傳統的處理方法，并將其引入馬爾可夫模型，從而應用于對水質的定量預測;李亞斌等[12]用樣本均值-均方差方法對銅川地區降水量進行分級，建立相應的馬爾可夫模型進行降水預測。

降水受氣候和人類活動兩者的共同影響，且由于氣候因素本身具有很強的變異性、復雜性以及多樣性，因此降水系統呈現出十分復雜的行為特征。過于復雜的系統難以建立精確的數學模型進行準確預測。筆者運用隨機模擬原理，在確定地區降水的分布模型后，結合蒙特卡洛方法以及馬爾可夫方法對固原市原州區的降水進行隨機模擬，以期預測未來原州區降水的發展變化趨勢，為水資源合理利用及調控提供依據。

2 研究方法

2.1 蒙特卡洛方法

蒙特卡洛方法又稱為概率統計法，是一種基于概率論思想，對隨機變量進行數理統計實驗及分布概率模擬，從而近似求解得到預測值的方法[13]。只要能構建出適當的模型，此方法都能夠進行模擬應用，其基本框架：①假設變量X服從某一概率分布;②用隨機抽樣的方法對概率分布進行抽樣從而得到樣本值，一般選擇常用的均勻分布模型，產生（0，1）區間內的隨機數，再結合原始數據產生服從特定分布的隨機序列，即樣本值;③確定和選取統計值;④由統計量的算術平均值得到統計量的估計值，從而近似求解出預測值。

2.2 馬爾可夫方法

2.2.1 馬爾可夫基本原理

馬爾可夫模型是基于馬爾可夫鏈建立起來的，馬爾可夫鏈是一種特殊的隨機過程[14]。設有一隨機運動的系統，它可能處的狀態記為E0、E1、…、En。這個系統只可能在時刻t（t=1，2，…，n）上改變它的狀態。隨著隨機運動的進行，定義一列隨機變量Xn（n=0，1，2，…），其中Xn=k，表示在t=n時，系統狀態為Ek。

2.2.2 模糊集理論中的級別特征值

使用傳統的馬爾可夫只能夠預測到某個區間，無法預測較為準確的降水值，在實際應用中作用有限，筆者選用模糊集理論中的級別特征值方法有效地解決了這個問題。

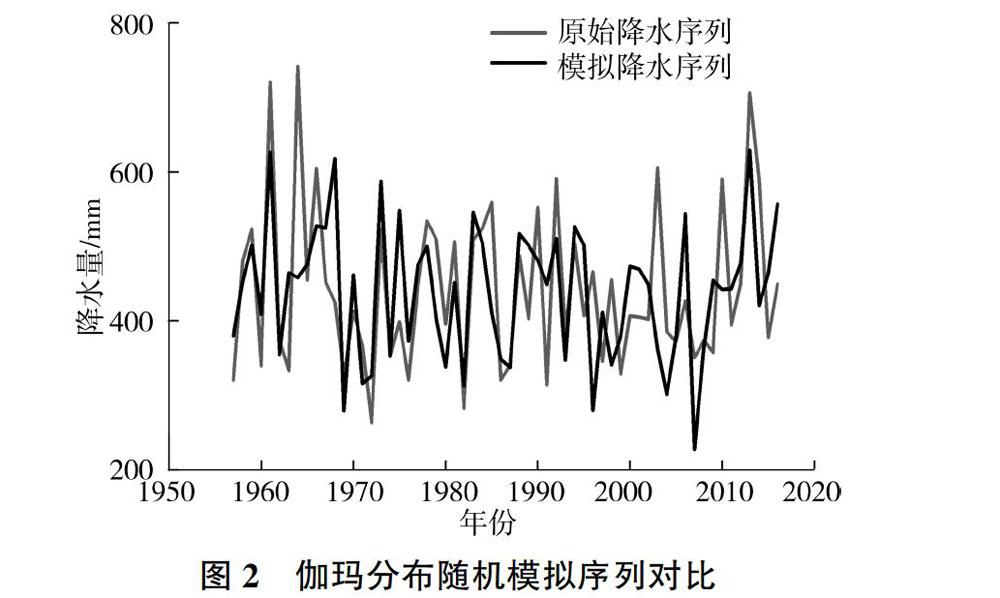
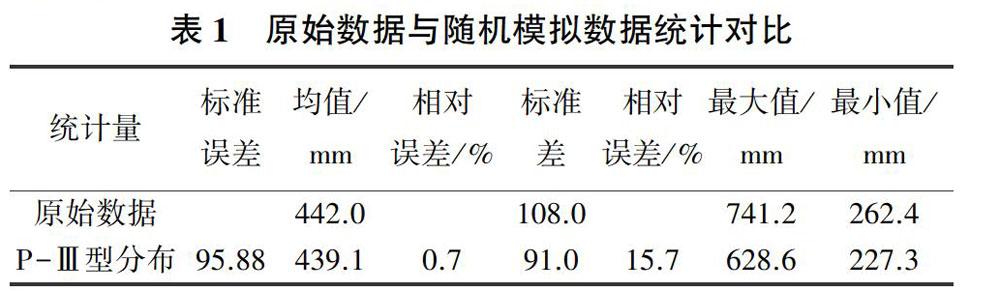
假定最大概率的狀態為i，當H>i時，年降水量的預測值X預報=TiHi+0.5;當H

2.3 K-S分布檢驗

K-S檢驗是用于檢測一組數據的分布與已知分布之間相似程度的一種檢驗方法，通過顯著性水平來判別是否相似。

設累積頻率曲線的理論分布形式為Fe（x），樣本的累積頻率F1（x）=k/n。其中：n為總觀測數，k為不大于x的次數。

3 原州區降水隨機模擬分析

3.1 原州區降水量理論分布函數

根據我國水文計算的相關規范，我國主要流域的降水量可假定服從P-Ⅲ型分布或對數正態分布[15]。通過計算機軟件用原始數據畫頻率曲線發現，當變差系數CV=0.26、偏態系數CS=0.52時，曲線模擬效果很好。又由P-Ⅲ型分布特性可知，當CS=2CV時，參數a0=0，此時的P-Ⅲ型分布就是伽瑪分布，故筆者采用a0=0的P-Ⅲ型分布，即伽瑪分布進行隨機模擬。因為筆者主要研究降水的隨機模擬，需要建立最為適合的模型，所以對兩種分布進行對比，選出最貼近原始數據的分布，從而建立最優模型。

3.1.1 伽瑪分布

3.1.2 對數正態分布

3.1.3 參數確定

通過原始降水數據可求得式（7）和式（8）的未知參數。由原始降水數據可知，原州區近60 a降水量的期望值為442.0 mm，方差為11 659.2 mm，從而求得對數正態分布參數μ為6.064、σ為0.234，伽瑪分布中的形狀參數α為14.80、尺度參數β為0.03。

3.1.4 對比分析

將原州區近60 a降水量的經驗分布分別與對數正態函數理論分布及伽瑪函數理論分布作對比，如圖1所示。可以看出，樣本數據與對數正態分布、伽瑪分布的擬合效果均較好，但無法進一步判斷最適合的理論分布，故筆者應用K-S檢驗對兩者進行概率分布判斷。

為了使結果更加精確，取置信度α=0.01，n=60，其K-S臨界值Dα（n）為0.206 7。當假設數據服從對數正態分布時，最大偏差D（n）為0.094 1;假設數據服從伽瑪分布時，最大偏差D（n）為0.107 6。通過對比分布的最大偏差與K-S檢驗臨界值，發現兩者均不能拒絕原假設，而且在99%的置信區間上符合對數正態分布及伽瑪分布。由此可知，原州區降水數據既服從對數正態分布，又服從P-Ⅲ型分布。此處選取一般水文規范所用到的P-Ⅲ型分布進行隨機模擬及預測研究。

3.2 降水量蒙特卡洛隨機模擬

借助計算機編程，引用均勻分布模型，通過蒙特卡洛方法產生（0，1）區間的隨機數，將產生的結果視為隨機變量概率。為了使模擬更具可靠性，使用伽瑪分布的反函數，根據原始降水序列的均值和方差，產生1 000 000組隨機降水序列值。用平方誤差作為評判標準，選取與原始降水序列數據平方誤差最小的一組作為隨機模擬降水量結果，見圖2。

將原始降水序列依次與通過伽瑪分布函數隨機模擬出的降水序列進行對比分析。可以看出，在伽瑪分布隨機模擬出的新降水序列中，整體波動較大，部分極值點在時間趨勢上保持一致。部分重要指標的對比見表1，伽瑪分布所模擬出來的均值、標準差等指標與原始數據相差不大，模擬效果良好，進一步證明了原始數據服從P-Ⅲ型分布的結論。

3.3 馬爾可夫降水預測驗證

當前對馬爾可夫預測準確度的評定大都是通過原始數據進行對比驗證，沒有考慮未來數據驗證的準確性。而從隨機模擬結果得到的P-Ⅲ型分布就可以很好地解決這個問題。筆者先通過對原始數據的預測及驗證判別馬爾可夫方法的可行性，之后再進行5 a預測，并進行K-S檢驗，判別其是否依舊符合P-Ⅲ型分布，從而確定預測結果的準確性。

3.3.1 分級標準及狀態確定

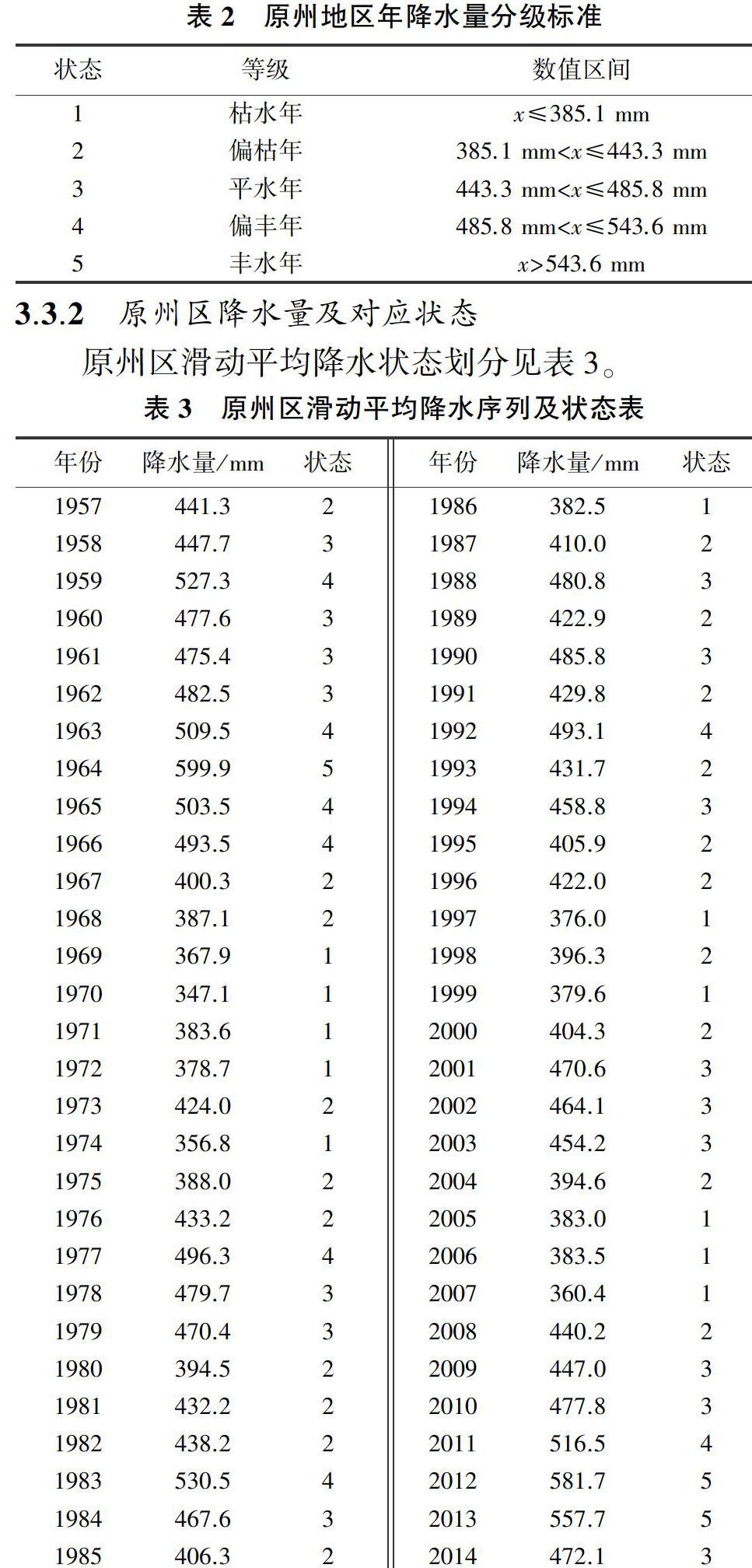
考慮到降水序列的連續性及降水特性，采取降水序列的3 a滑動平均值進行降水預測。考慮水文現象的本身特性及序列數據的結構合理性，將降水量序列分為5類，即將降水量劃分為5個區間，分別為枯水年、偏枯年、平水年、偏豐年、豐水年，采用基于歐氏距離的層次聚類法進行分級，見表2，其中x為年降水量。

3.3.3 相關系數與權重的確定

3.3.4 模型檢驗及分析

基于隨機模擬出的2007—2011年的年降水數據，采用加權馬爾可夫模型對2012年降水量進行預測，結果見表5，2012年的預測值為狀態3，根據模糊集理論，級別特征值為2.824，2012年的降水量預測值為500.8 mm，相對誤差為13.9%，在中長期水文預報允許誤差20%之內。2013年、2014年預測值分別為521.4、499.5 mm，相對誤差分別為6.5%、5.8%，都在允許誤差以內。

通過以上對原始數據的驗證，能在一定程度上證明加權馬爾可夫模型在降水預測應用上的可行性。但是，其只能對未來降水進行預測，并不能對未來降水預測的準確性進行檢驗，要確保對未來預測的準確性，還需要進一步的驗證。由于前文已經得到寧南地區降水符合P-Ⅲ型分布，因此筆者通過對寧南山區降水進行接下來3 a滑動平均的預測，再通過K-S檢驗，看是否滿足P-Ⅲ型分布，預測結果見表6。

此時，n=63，取置信度α=0.01，其K-S臨界值Dα（n）為0.201 8，假設數據服從P-Ⅲ型分布，最大偏差D（n）為0.080 6。通過對比分布的最大偏差與K-S檢驗臨界值，發現不能拒絕原假設，而且在99%的置信區間上符合P-Ⅲ型分布。可見，對未來5 a的降水預測結果是可靠的。

4 結 論

（1）依據原州區1957—2016年實測降水資料，運用蒙特卡洛方法進行隨機模擬，通過K-S檢驗，得出原州區降水符合P-Ⅲ型分布。

（2）通過對降水數據進行3 a滑動平均處理，采用基于歐氏距離的層次聚類法進行狀態劃分，確定了枯水年、偏枯年、正常年、偏豐年和豐水年5個狀態，建立了滑動平均-加權馬爾可夫鏈預測模型。

（3）通過對2012年、2013年、2014年滑動平均降水量的預測，得出馬爾可夫降水預測模型可以應用于原州區降水預測。

（4）對未來5 a降水進行預測，預測值分別為508.5、520.8，554.9、451.0、466.6 mm，通過K-S檢驗進行驗證，證明了預測的準確性。

參考文獻：

[1] 魏艷華，王丙參.概率論與數理統計[M].成都：西南交通大學出版社，2013：264-269.

[2] 丁晶，鄧育仁.隨機水文學[M].成都：成都科技大學出版社，1988：9-10.

[3] 劉新立.隨機過程與隨機模擬在水災風險管理中的應用研究[J].經濟科學，2003（1）：114-119.

[4] 尹正杰，袁宏源，崔遠來，等.灌區灌溉需水量的隨機模擬[J].中國農村水利水電，2001（11）：19-22.

[5] 溫季，郭樹龍，盧聞航.作物灌溉隨機模擬技術研究[J].人民黃河，2004，26（5）：39-41.

[6] ZHANG J L， LI Y P， HUANG G H， et al. Assessment of Parameter Uncertainty in Hydrological Model Using a Markov-Chain-Monte-Carlo-Based Multilevel-Factorial-Analysis Method[J].Journal of Hydrology， 2016， 538（7）：471-486.

[7] KNIGHTON J， WHITE E， LENNON E， et al. Development of Probability Distributions for Urban Hydrologic Model Parameters and a Monte Carlo Analysis of Model Sensitivity[J].Hydrological Processes， 2015， 28（19）：5131-5139.

[8] 劉悅憶，趙建世，黃躍飛，等.基于蒙特卡洛模擬的水質概率預報模型[J].水利學報，2015，46（1）：51-57.

[9] 李娟，張維江，馬軼.滑動平均-馬爾可夫模型在降水預測中的應用[J].水土保持研究，2005，12（6）：200-202，209.

[10] 王艷，毛明志，范晶，等.最優分割法確定的加權馬爾可夫鏈在降雨量預測中的應用[J].統計與決策，2009，25（11）：17-18.

[11] 岳遙，李天宏.基于模糊集理論的馬爾可夫模型在水質定量預測中的應用[J].應用基礎與工程科學學報，2011，19（2）：231-242.

[12] 李亞斌，徐盼盼，錢會，等.加權馬爾可夫鏈在銅川地區降水量預測中的應用[J].灌溉排水學報，2017，36（5）：96-102.

[13] GARCA-ALONSO C R， ARENAS-ARROYO E， PREZ-ALCAL G M. A Macro-Economic Model to Forecast Remittances Based on Monte-Carlo Simulation and Artificial Intelligence[J].Expert Systems with Applications， 2012， 39（9）：7929-7937.

[14] 夏樂天.馬爾可夫鏈預測方法及其在水文序列中的應用研究[D].南京：河海大學，2005：11-12.

[15] 夏樂天，朱元甡.馬爾可夫鏈預測方法的統計試驗研究[J].水利學報，2007，38（增刊1）：372-378.

【責任編輯 張 帥】