動態更新屬性值變化時的最優粒度
劉鳳玲,林國平
(閩南師范大學 數學與統計學院,福建 漳州 363000)
1 引 言
數據規模隨著信息技術的迅速發展而不斷膨脹,粒計算常用于處理復雜的數據系統.粒計算是將所需探究的論域劃分成若干相對簡單的粒,簇、塊或集合構成了這些粒.
Zadeh于1979年首次提出模糊信息粒這一概念[1].隨后,相關應用背景的粒計算模型與方法相繼被提出[2-5].信息粒在解決復雜問題中起重要作用,其可將較為復雜的信息系統抽象地轉化為若干相對簡單的信息系統,這樣既可以降低處理難度,又可以提高預測信息的準確性.
在大部分信息系統中,同一對象在同一個屬性下只有一個屬性值,這使得人們只能從固定的粒度或視角分析數據信息.然而,在實際應用中,根據實際問題的不同需要,同一個對象在同一個屬性下可以取不同粒度層次標記的值. 例如,需要評定獎學金時學生的考試成績一般記錄為0~100之間的數,需要知曉成績優秀、較好等級別的人數時可以將成績記為“優秀”、“較好”、“中等”、“差”. 進一步的,如果需要,還可以將其分為兩個值,比如給予學位認定時記為“合格”和“不合格”.基于此,Wu等人根據對象在決策系統中擁有不同的粒度標記,于2011年首次給出了多粒度標記決策系統的概念[6].近年來,基于多粒度標記劃分的粗糙集數據分析方法得到不斷完善和發展,多粒度標記決策系統是人們研究的熱點. 目前,查閱相關文獻發現學者們主要從最優粒度選擇[7-17]、規則約簡或提取[18,19]及知識表示[20]等方面對多粒度標記決策系統進行研究. 從系統的協調性與完備性的角度來看,學者們主要研究了協調且完備的、協調不完備的以及不協調但完備的這三種多粒度標記決策系統.在實際應用中,多粒度標記決策系統是常被用于各種信息分析,如被廣泛應用于數據挖掘、圖像處理、人工智能、地理信息甄別和軍事技術等領域.
如今是大數據時代,在許多實際情況下,由于各種需求或人為失誤,數據可能會發生變化.因此,需要對動態數據集中隱藏的知識進行相應的更新. 增量更新機制是利用前面獲得的計算結果來獲取動態數據集中的知識而不是重新從頭開始計算.在動態環境中,目前基于粗糙集理論的增量更新方法主要涉及對象的變化[21-23]、屬性的變化[24,25]以及屬性值的變化[26,27].而有關多粒度標記決策系統方面的動態更新,本人只查閱到學者們討論了在多粒度決策系統中,對象更新環境下選擇最優粒度的策略并設計了相應的算法.
事實上,在實際應用中人為或其他因素難免不出現收集到的多粒度標記決策系統在某個粒度標記下的屬性值是錯誤的,而此時則需要將正確的屬性值更新進去,從而得正確的數據,即此時新的系統屬性值發生了更新.若當前粒度尺度下屬性值發生變化,則粗于該粒度尺度的粒度尺度可能也隨之發生變化.一般來說,在多粒度標記系統中等級越小的粒度越細,然而粒越細獲取知識的成本越高,因此選擇合適的粒度級別來獲取規則及求目標近似集等較為重要,即最優粒度選擇是多粒度標記系統中的知識獲取較為關鍵的一步.基于此,本文針對屬性值變化環境下的不協調多粒度決策系統最優粒度的選擇進行研究.
由于WU在文獻[9]中分析了不協調多粒度決策系統中8種不協調性選擇最優粒度的對比,指出實際上只有4種:分布協調; 最大分布協調;而分配協調、似然協調、上近似協調及廣義協調互相等價; 下近似協調與信任協調等價.基于此,本文將只討論4種協調性下屬性值變化環境下的不協調多粒度決策系統選擇最優粒度的策略:分布協調、最大分布協調、上近似協調及下近似協調.
2 基本知識
2.1 多粒度標記決策系統的概念
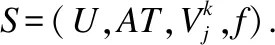
在多粒度標記系統中,每一個屬性aj∈AT均為多粒度標記屬性,也即對于同一個對象x∈U在不同粒度層面下有不同的取值.為方便討論,本文約定沒有特別說明情況下在同一系統中,所有條件屬性的粒度層次均為I.
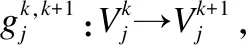
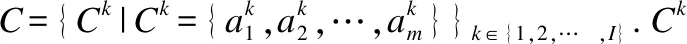
對任意的Ck?C,將論域U在Ck下的等價關系、等價類及等價劃分分別記為:
類似記:Rg0gggggg={(x,y)∈U×U|fg0gggggg(x)=fg0gggggg(x)},[x]g0gggggg={y∈U|(x,y)∈Rg0gggggg},U/Rg0gggggg={[x]g0gggggg|x∈U}={D1,D2,…,Dr},r為決策類劃分的個數,即r=|U/Rg0gggggg|.
對于論域U中的一個子集X,其關于RCk的下近似和上近似分別為:
若對任意的[x]RCk∈U/RCk,總存在[x]Rd∈U/Rg0gggggg使得[x]RCk?[x]Rd成立,則記RCk?Rd.
假設dIS=(U,C∪g0gggggg)為一個多決策的多粒度標記決策系統,該系統中所有條件屬性均有I個等級粒度,則dIS=(U,C∪g0gggggg)可分解為I個信息系統,也即dIS=dIS1∪dIS2∪…∪dISI.
2.2 不協調多粒度標記決策系統的協調性與最優粒度選擇
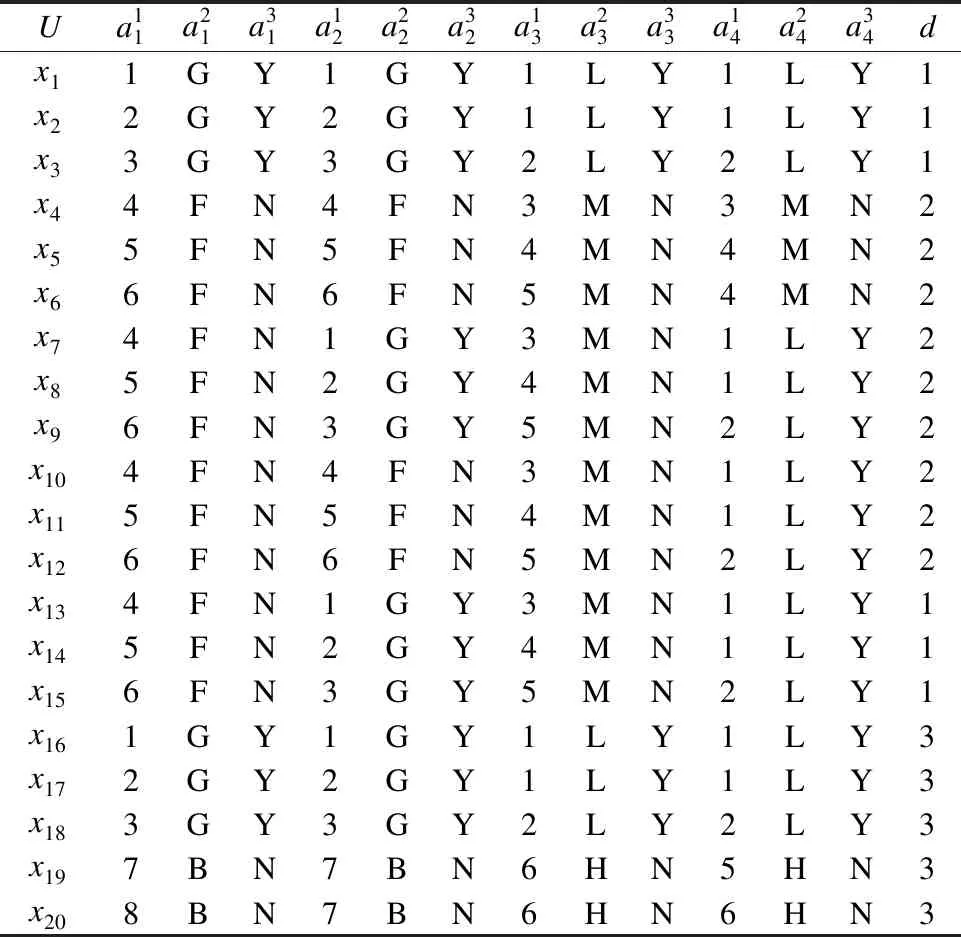
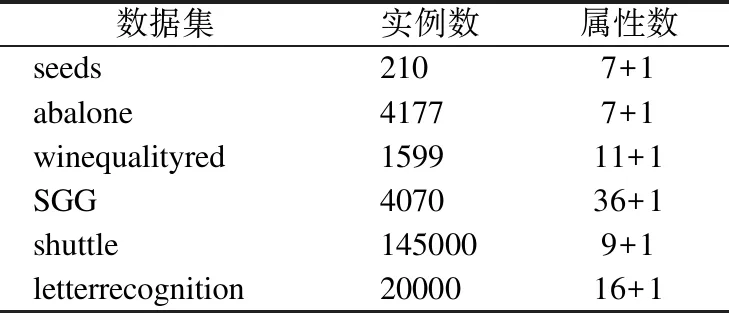
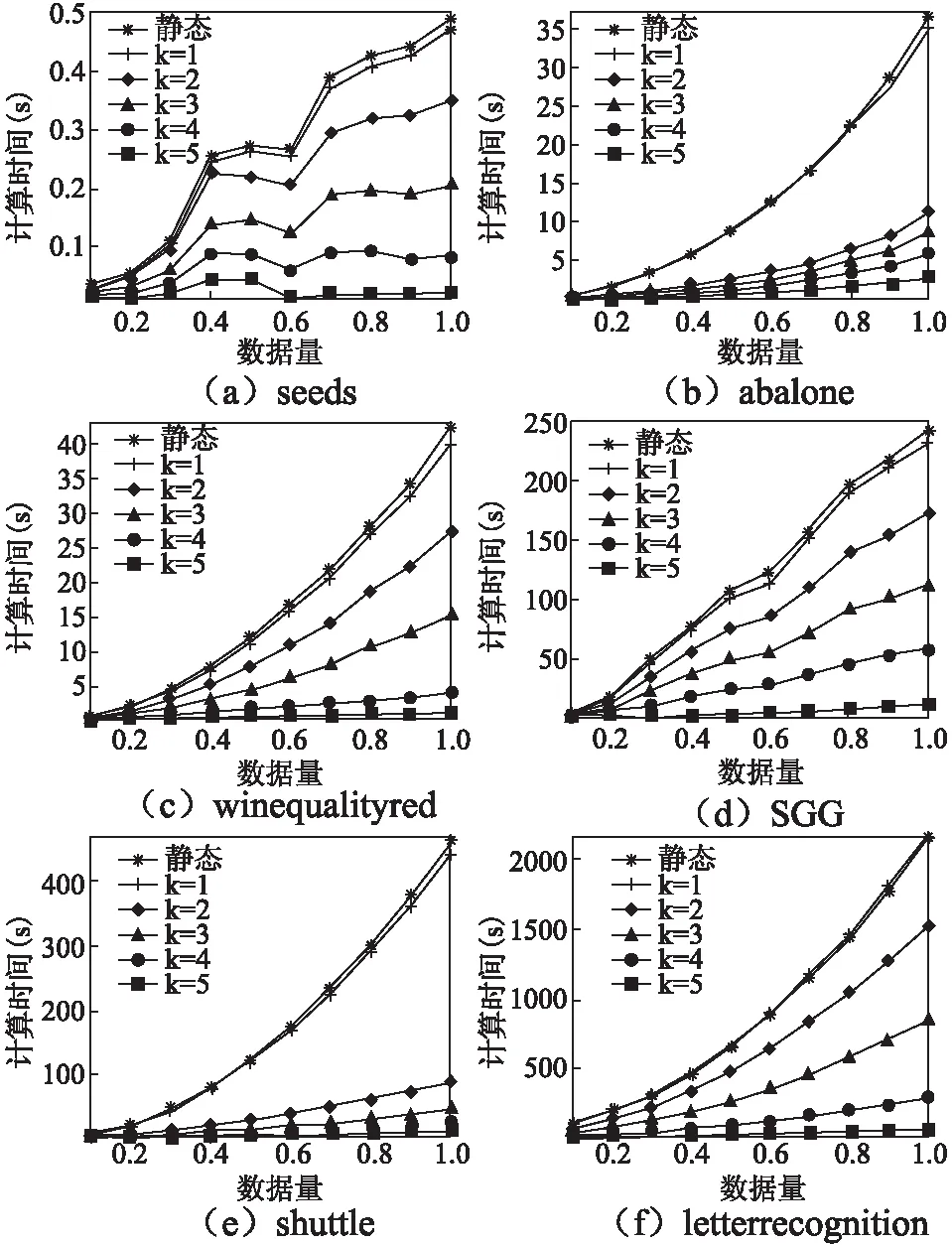
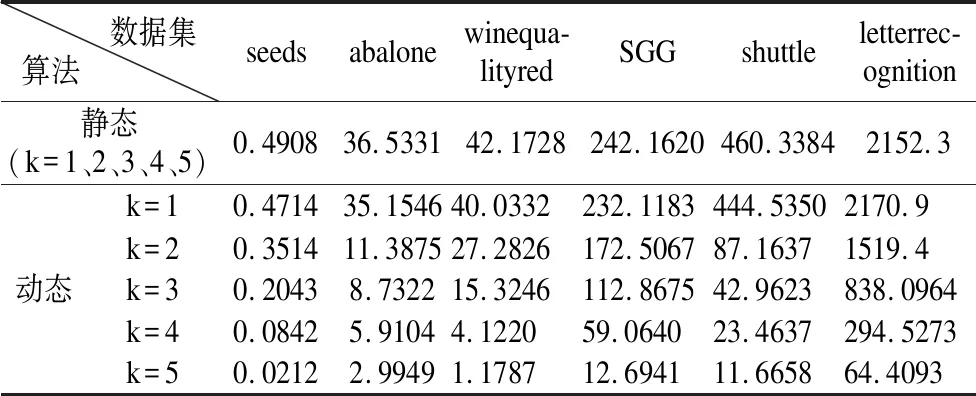
定義3[6].設dIS=(U,C∪g0gggggg)為多粒度決策系統,若RC1?Rd,則系統dIS是協調的.若進一步滿足RCk?Rd,則稱dISk=(U,Ck∪g0gggggg)協調.若dISk=(U,Ck∪g0gggggg)協調,則對任意的k′ 定義4[9].設dIS=(U,C∪g0gggggg)為不協調的多粒度決策系統,則 1)如果LCk(d)=LC1(d),就稱dISk關于dIS下近似協調.若dISk關于dIS下近似協調,但若k+1≤I,dISk+1關于dIS不是下近似協調,那么S的下近似最優粒度為第k粒度層次. 2)如果HCk(d)=HC1(d),就稱dISk關于dIS上近似協調.若dISk關于dIS上近似協調,但如果k+1≤I,dISk+1關于dIS不是上近似協調,那么S的下近似最優粒度為第k粒度層次. 3)如果對任意的x∈U,有μCk(d)=μC1(d),就稱dISk關于dIS分布協調.若dISk關于dIS分布協調,但若k+1≤I,dISk+1關于dIS不是分布協調,那么S的分布最優粒度為第k粒度層次. 4)如果對任意的x∈U,有γCk(d)=γC1(d),就稱dISk關于dIS最大分布協調.若dISk關于dIS最大分布協調,但若k+1≤I,dISk+1關于dIS不是最大分布協調,那么S的最大分布最優粒度為第k粒度層次. 定理1.設在t時刻,不協調多粒度決策系統為dIS(t)=(U,C∪g0gggggg),且系統dIS(t)的下近似最優粒度層次為第kt粒度層次;在t+1時刻,k′ 1)當k>kt+1時,則kt+1=kt; 2)當k≤kt+1時,若dISk關于dISt+1不是下近似協調的,則kt+1=k-1;若dISk關于dISt+1是下近似協調的,則判斷k+1的下近似協調性,若dISk+1關于dISt+1是下近似協調的,則繼續判斷k+2的下近似協調性,以此循環,直至k+m關于dISt+1不是下近似協調的,則kt+1=k+m-1. 證明:在t時刻,系統dIS(t)的下近似最優粒度層次為第kt粒度層次,則由定義4易知,對任意的k′≤kt,dISk′均關于dISt是下近似協調的;dISkt+1關于dISt不下近似協調. 1)若k>kt+1,則說明在t+1時刻,任意的k′≤kt+1所對應的屬性值均未發生變化.此時對任意的k′≤kt+1,dISk′均關于dISt+1是下近似協調的,又dISkt+1關于dISt+1不是下近似協調的,從而由定義4可知t+1時刻系統的下近似最優粒度為kt.即可得kt+1=kt. 2)若k≤kt+1,則說明任意的k′≤k-1所對應的屬性值均未發生變化.即此時對任意的k′≤k-1,dISk′均關于dISt+1是下近似協調的.若dISk關于dISt+1不是下近似協調的,又dISk-1關于dISt+1是下近似協調的,則由定義4可知t+1時刻系統的下近似最優粒度層次為k-1;若dISk關于dISt+1下近似協調則由定義4中的(1)可知成立. 下面給出例子來分析及理解所提出的定理. 例1.如表1為一個多粒度標記決策系統,記為dIS=(U,C∪g0gggggg).該表的條件屬性有三個粒度層次,其中“G,F,B,S,M,L,Y,N”分別表示“好,中等,差,小,中,大,是,否”.按粒度層次該信息表可分解為三個信息表,即dIS=dIS1∪dIS2∪dIS3,其中, 表1 多決策的多粒度標記信息表Table 1 Multi-granular labeled table with multi-decision 定理2.設在t時刻,不協調多粒度決策系統為dIS(t)=(U,C∪g0gggggg),且系統dIS(t)的上近似最優粒度層次為第kt粒度層次;在t+1時刻,k′ 1)當k>kt+1時,則kt+1=kt; 2)當k≤kt+1時, 若dISk關于dISt+1不是上近似協調的,則kt+1=k-1; 若dISk關于dISt+1是上近似協調的,則判斷k+1的上近似協調性,若dISk+1關于dISt+1是上近似協調的,則繼續判斷k+2的上近似協調性,以此循環,直至k+m關于dISt+1不是上近似協調的,則kt+1=k+m-1. 定理3.設在t時刻,不協調多粒度決策系統為dIS(t)=(U,C∪g0gggggg),且系統dIS(t)的分布最優粒度層次為第kt粒度層次;在t+1時刻,k′ 1)當k>kt+1時,則kt+1=kt; 2)當k≤kt+1時, 若dISk關于dISt+1不是分布協調的,則kt+1=k-1; 若dISk關于dISt+1是分布協調的,則判斷k+1的分布協調性,若dISk+1關于dISt+1是分布協調的,則繼續判斷k+2的分布協調性,以此循環,直至k+m關于dISt+1不是分布協調的,則kt+1=k+m-1. 定理4.設在t時刻,不協調多粒度決策系統為dIS(t)=(U,C∪g0gggggg),且系統dIS(t)的最大分布最優粒度層次為第kt粒度層次;在t+1時刻,k' 1)當k>kt+1時,則kt+1=kt; 2)當k≤kt+1時, 若dISk關于dISt+1不是最大分布協調的,則kt+1=k-1; 若dISk關于dISt+1是最大分布協調的,則判斷k+1的最大分布協調性,若dISk+1關于dISt+1是最大分布協調的,則繼續判斷k+2的最大分布似協調性,以此循環,直至k+m關于dISt+1不是最大分布協調的,則kt+1=k+m-1. 下面以下近似協調為例給出相應的靜態算法和動態算法. 算法1.靜態:多粒度決策系統的最優粒度選擇 輸入:t+1時刻求得的多粒度決策系統dIS(t+1)=(U,C∪g0gggggg). 輸出:多粒度決策表的最優粒度kt+1. Step1.計算決策劃分U/Rd={D1,D2,…,Dr},k′=1; Step2.當k′=1:|I|時,則計算[x]Ck′(x∈U); Step3.當k′=1:|I|時,求出LCk′(d); Step4.判斷LCk′(d)與LC1(d) 的關系,若LCk′(d)≠LC1(d),則kt+1=kt-1,停止運算.若LCk′(d)=LC1(d),則轉Step 5. Step5.若k′+1>I,則kk+1=k′,停止運算;若k′+1≤I,則k′=k′+1,并轉到Step 2. 算法2.動態:多粒度決策系統在屬性值更新環境下的最優粒度選擇 輸入:t時刻求得的多粒度決策系統dIS(t)=(U,C∪g0gggggg)及其最優粒度層次kt及其決策劃分{D1,D2, …,Dr}、t+1時刻的多粒度決策系統dIS(t+1),屬性值變化的最小粒度層次k. 輸出:多粒度決策表在屬性值更新之后的最優粒度kt+1. Step1.判斷k與kt+1的大小關系,若k>kt+1,則轉Step2;若k≤kt+1,則轉Step3; Step2.kt+1=kt,停止運算; Step3.當k′=k:|I|時,求出LCk′(d);判斷LCk′(d)與LC1(d) 的關系,若LCk′(d)≠LC1(d),則kt+1=kt-1,停止運算,若LCk′(d)=LC1(d),則轉Step 4. Step4.若k′+1>I,則kt+1=kt,停止運算;若k′+1≤I,則k′=k′+1,并轉回Step 3. 這部分通過在6個UCI數據集來比較靜態和動態算法的計算性能.6個數據集的相關信息見表2. 表2 數據集描述Table 2 Data set description 在這個實驗中,比較了隨著數據規模增大,靜態和動態算法的執行時間.所有的算法運行在個人電腦,配置Windows 7,Intel(R)Core(TM)i7-3632QM CPU 2.20GHz,4GB內存.編程語言matalb. 將預處理好的每個數據集分割為等大小的10份.第1份作為第1個數據集,第1和第2份的組合作為第2個數據集,第2個數據集和第3份數據的組合作為第3個數據集,以此類推,全部10份的數據組合作為第10個數據集.10個數據集的目標概念都使用所對應的數據集的決策類.這10個數據集可以用來觀察靜態和動態算法執行時間隨著數據集規模增大的變化情況. 在本小節中,不失一般性,對于所有粒度標記下屬性值變化的可能都進行了實驗,即對k=1,2,3,4,5這五種情況都進行了靜態和動態的實驗.由于k=1,2,3,4,5時靜態算法的計算時間一致,故本文只羅列一次.為了公平,兩個算法沒有進行其它的優化. 圖1 靜態和動態算法最優粒度選擇的計算時間比較Fig.1 Comparison of computation time of optimal scale selection between static and dynamic algorithms 實驗結果見圖1和表3.圖1展示了兩個算法計算時間隨數據集規模的變化情況.從圖1(x軸表示數據集占總數據的比例,y軸表示計算時間)不難發現,對于相同的大小的數據集,當k≥2時靜態最優粒度選擇算法時間消耗一致地低于靜態最優粒度選擇算法.另外,在大多數數據中,計算時間的差值隨著數據的增加而增大.k=1時計算時間基本持平.表3展示了兩個算法在6個數據集各自產生的第10個數據集上的運行時間.結果顯示局部多粒度下近似算法僅僅花費了相應全局算法的十分之一執行時間. 表3 靜態和動態算法計算時間比較(時間:秒)Table 3 Comparison of computation time between static and dynamic algorithms(time:s) 研究了某個粒度下屬性值變化時最優粒度的選擇策略,并設計了相應的靜態和動態最優粒度選擇算法并進行了相關實驗.實驗結果表明,新提出的方法可以對于屬性值變化的系統可以有效進行選擇最優粒度,且設計的動態最優粒度選擇算法在一定程度上提高了計算效率.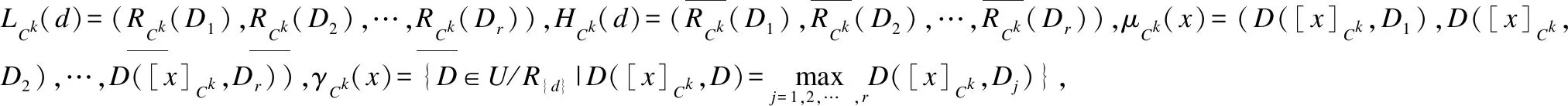
3 屬性值變化環境下的不協調多粒度決策系統的最優粒度選擇
4 屬性值變化環境下的不協調多粒度決策系統的最優粒度選擇算法
5 實驗分析
6 結 語

