基于信息匹配度的混合推薦算法

任靜霞，武志峰

（天津職業技術師范大學信息技術工程學院，天津 3002222）

推薦系統[1]是大數據背景下，降低信息過載、幫助服務商精準提供用戶所需信息的一種解決方案，被廣泛應用于各大電子商務網站。推薦系統利用收集到的用戶喜好或者物品信息特性等進行訓練，得到用戶-物品推薦模型，從而預測用戶未來可能會感興趣或者需要的物品，為用戶提供定制化服務。實現推薦系統的推薦算法有協同過濾推薦算法、基于內容的推薦算法、基于知識的推薦算法、基于關聯規則的推薦算法等，其中協同過濾算法（collaborative filtering，CF）使用最為廣泛，但是冷啟動問題無法得到解決，在稀疏矩陣中性能下降，可擴展性差；基于內容的推薦算法要求內容能夠容易抽取成有意義的特征，并且要求特征內容有良好的結構性，但其可解釋性差；而基于知識的推薦算法存在知識難以獲取的問題，要求用戶需求明確且需求具有可推薦性。正因為以上算法均有不足之處，所以研究者們一直致力于追求適應性更強、推薦質量更高的推薦算法。

為提高推薦質量獲得較好的推薦結果，前人做了大量研究。如冷亞軍等[2]對協同過濾技術進行了總結；饒鈺等[3]通過融合評分向量間余弦值和均方差值改進協同過濾算法；Koren 等[4]對推薦系統中現有的矩陣分解技術進行了分析綜述；王娟等[5]提出將矩陣分解的結果應用于基于用戶的最近鄰推薦；劉沛文等[6]將不同用戶對于不同物品的個性化行為特征指數引入相似度的計算中；李鵬飛等[7]將物品屬性相似性和改進的修正余弦相似性線性組合作為相似性度量方法；蘇曉云等[8]提出一種基于動態加權的混合協同過濾算法，考慮了項目近鄰和隱藏特征這2 個因子并進行權重計算，提高推薦精度。本文在傳統推薦方法的基礎上，提出了一種新的基于推薦信息匹配度的協同過濾和矩陣分解的動態權重混合算法（UIBCF-MF），該算法根據某一用戶和物品的近鄰推薦與已有信息的不匹配度動態調整權重，與傳統單個算法相比，既能發揮各算法優勢，又能改善其準確性和可擴展性。

1 協同過濾算法

協同過濾算法[9]采用 K 近鄰（k-nearest neighbor，KNN）技術，從用戶角度出發，通過用戶的歷史喜好信息分析各個用戶之間的相似度或者物品之間的相似度，然后利用目標用戶的最近鄰用戶，或是目標物品的最近鄰物品，以其對商品評價的加權評價值來預測用戶對特定商品的喜好程度，系統根據這一喜好程度進行推薦。協同過濾算法依賴于準確的用戶評分，計算過程中熱門商品被推薦幾率更大，存在冷啟動問題，無法對新用戶或物品進行處理，不適用于生存周期短的物品。協同過濾算法分為基于用戶的協同過濾（user-based CF）和基于物品的協同過濾（item-based CF）[10]2 種。

1.1 基于用戶的協同過濾

user-based CF 適用于用戶交互性強或者用戶數量相較物品數量變化較穩定的情況。定義推薦系統中，U={u1，u2，…，um}為 m 個用戶的集合，I={i1，i2，…，in}為n 個物品的集合，R[m×n]為用戶-物品評分矩陣，rui為用戶 u 對物品 i 原始評分值為用戶 u 對物品 i預測評分值，user-based CF 所得預測評分為

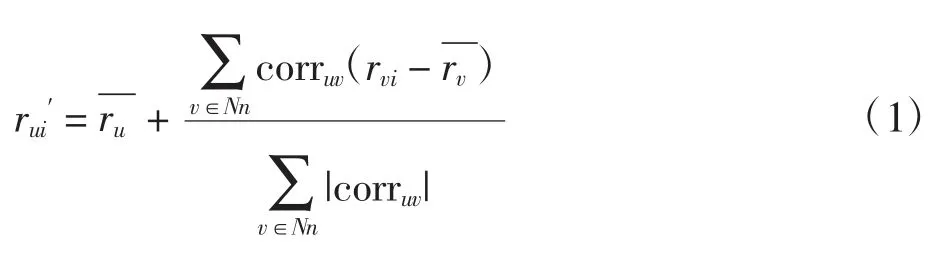
1.2 基于物品的協同過濾

item-based CF 適用于物品數量變化明顯小于用戶數量變化的情況。定義推薦系統中，U={u1，u2，…，um}為 m 個用戶的集合，I={i1，i2，…，in}為 n 個物品的集合，R[m ×n]為用戶-物品評分矩陣，rui為用戶 u 對物品i 原始評分值為用戶u 對物品i 預測評分值，item-based CF 所得預測評分為

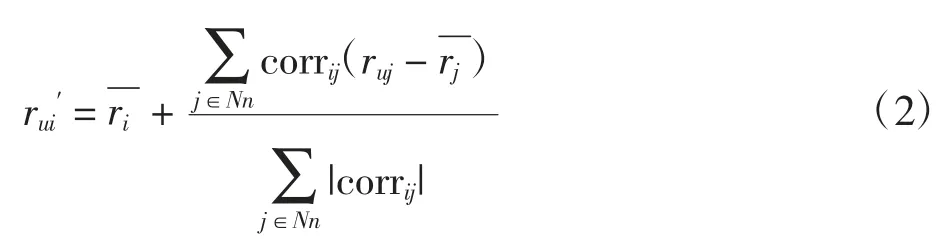
1.3 相似度計算

適用于推薦系統的相似性度量方法有很多，使用較多的有皮爾遜相關系數、余弦相似度和歐式距離等。

1.3.1 皮爾遜相關系數

計算公式

式中：corr 為相關系數，值在[-1，1]，corr=0 時，u、v 不相關；|corr|越大，u、v 相關性越強。

1.3.2 余弦相似度

計算公式

式中：cos Sim 為 u、v 間相似度。

1.3.3 歐氏距離

計算公式

式中：d 為 u、v 間歐氏距離。

2 矩陣分解算法

矩陣分解算法（matrix factorization，MF）[11-12]是基于模型的推薦算法中的一種，通過將歷史用戶-物品信息矩陣進行分解，再用分解后的矩陣預測未知評分，從而完成推薦。矩陣分解很好地解決了評分數據稀疏性問題，易于編程實現，具有可擴展性，但其模型訓練過程耗時較長且解釋性不強。

2.1 矩陣分解模型

定義推薦系統中，U={u1，u2，…，um}為 m 個用戶的集合，I={i1，i2，…，in}為 n 個物品的集合，R[m × n]為用戶-物品評分矩陣，將矩陣R 分解為2 個矩陣Pm×k和Qk×n的乘積，Rm×n≈Pm×k× Qk×n=R′，其中，矩陣 P 為用戶隱含特征矩陣；矩陣Q 為物品隱含特征矩陣為用戶u 對i 物品預測評分值。MF 所得預測評分為

式中：p、q 分別由矩陣 P、Q 經隨機梯度下降算法得到。

2.2 隨機梯度下降算法

隨機梯度下降算法是機器學習較常見的一種優化算法。將原始評分矩陣R 和重新構建的評分矩陣R′之間誤差的平方作為損失函數[13]，利用梯度下降法求解損失函數最小值，為了獲得較好的泛化能力，在損失函數中加入正則項，得到損失函數

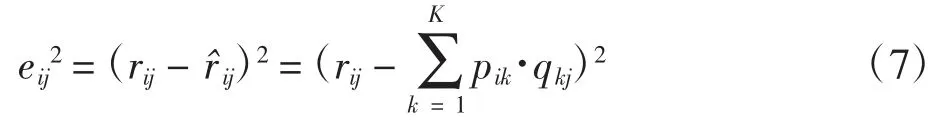
損失函數負梯度為

得到更新變量公式

通過迭代，直到算法收斂，得到p、q。

3 UIBCF-MF 算法

算法首先采用單一傳統user-based CF、item-based CF 和MF 推薦算法進行評分預測，再根據3 種算法所得預測評分與歷史數據間不匹配度動態調整各算法權重從而實現最終評分預測，針對冷啟動問題采用二次矩陣分解辦法。算法分為3 個部分：①通過KNN計算預測評分時提出的一種新的主觀評分規范化方法；②針對不同情況下的3 種推薦算法進行加權混合；③當新用戶或新物品出現時采用冷啟動處理方法。

3.1 主觀評分規范化

在進行傳統user-based CF 和item-based CF 評分預測時，考慮到鄰居用戶或物品與目標用戶或物品的評分習慣不同造成的評分差異，在使用皮爾遜相關系數計算相似性，通過最近鄰進行評分預測時，提出一種適用于不同評分區間的評分規范化方法。以基于用戶的最近鄰為例，定義用戶v 對用戶u 影響因子為fv，則 user-based CF 所得預測評分 rui′為

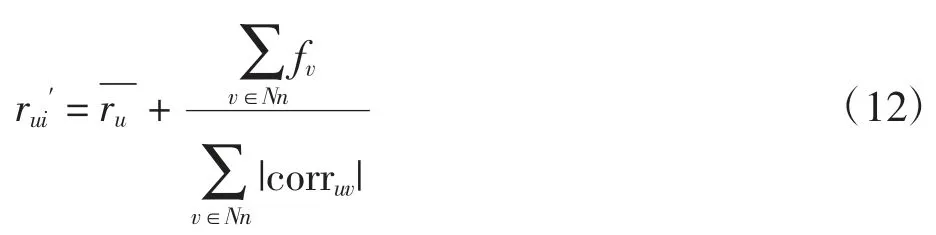
進行評分規范化的評分預測步驟如下。

輸入：原始用戶-物品評分rui，用戶或物品近鄰列表。

輸出：用戶v 對用戶u 影響因子fv。

步驟1 評分區間為[rmin，rmax]，計算用戶u 與近鄰用戶v 間相關系數corruv。

步驟 2 若 corruv＞ 0，則為正相關，fv值由式（13）求得；反之，若 corruv＜ 0，則為負相關，fv值由式（14）求得

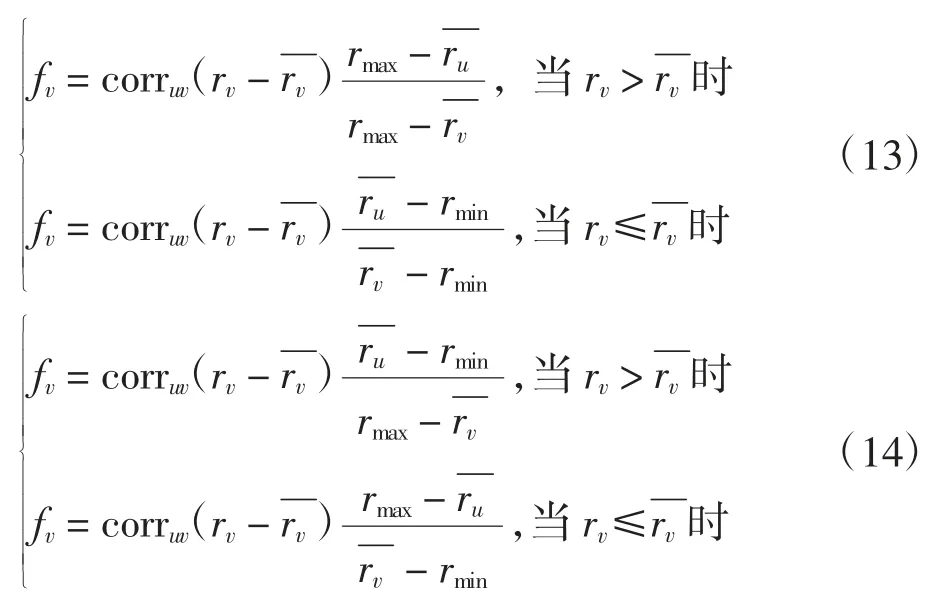
3.2 加權混合預測

定義R[m×n]為原始用戶-物品評分矩陣，rui為用戶u 對物品i 原始評分值，由user-based CF、item-based CF 和MF 算法得到預測評分矩陣R1[m×n]、R2[m×n]和 R3[m × n]、r1ui、r2ui、r3ui分別為矩陣 R1、R2、R3 中用戶u 對物品i 評分，經加權混合算法得到最終評分預測矩陣R4[m × n]，其中用戶u 對物品i 評分值為r4ui。

算法思想：對于評分矩陣中每一個評分r，計算user-based CF，item-based CF 和 MF 3 種算法所得預測評分r 與原始評分rui匹配度，從而動態調整權重。若原始評分rui不為空而某一算法預測評分為空，則認為該算法推薦不合理，調整各算法對該評分值影響，降低該算法影響度；若存在多個合理推薦值，則根據匹配度擇優選擇。

混合算法步驟如下。

輸入：原始用戶-物品評分rui，基于用戶的協同過濾預測評分r1ui，基于物品的協同過濾預測評分r2ui，矩陣分解預測評分r3ui。

輸出：加權混合預測評分r4ui。

步驟1 根據輸入的評分，定義w1、w2、w3 為加權因子，len為物品數，當rui值不為空時，統計r1ui空值個數 a，r2ui空值個數 b。

步驟2 若rui值為空，執行步驟3，否則執行步驟6。

步驟3 若r1ui值為空，執行步驟4，否則執行步驟5。

步驟4 若r2ui值為空，r4ui=r3ui，結束算法。否則w1r1ui+w2r2ui+w3r3ui，結束算法。

步驟5 若r2ui值為空結束算法。否則結束算法。

步驟6 若r1ui值為空，執行步驟7，否則執行步驟8。

步驟7 若r2ui值為空，r4ui= r3ui，結束算法。否則選擇 |r2ui-rui|與|r3ui-rui|較小值賦給r4ui，結束算法。

步驟 8 若 r2ui值為空，選擇|r1ui-rui|與|r3ui-rui|較小值賦給r4ui，結束算法。否則選擇|r1ui-rui|、|r2ui-rui|與|r3ui-rui|較小值賦給r4ui，結束算法。

3.3 冷啟動問題

在推薦系統中，傳統user-based CF 和item-based CF 算法利用已有歷史數據構建推薦模型，故當新用戶或新物品出現時，算法無法給出相應推薦，冷啟動問題無法解決。UIBCF-MF 算法利用MF 算法能有效解決冷啟動問題這一思路解決上述問題，解決方式如下。

對于用戶冷啟動，提出新用戶，對提取后剩余的待測數據 R[m′× n]使用 user-based CF、item-based CF和MF 算法進行評分預測分別得到評分矩陣R1[m′×n]、R2[m′× n]和 R3[m′× n]，通過 UIBCF-MF 算法中混合加權方法得到預測結果矩陣R4[m′× n]，添加已提出新用戶數據到該矩陣得到矩陣R4′[m×n]，并使用MF 算法進行二次矩陣分解得到最終預測結果矩陣R4[m × n]。

對于物品冷啟動，提出新物品，對提取后剩余的待測數據 R[m × n′]使用 user-based CF、item-based CF和MF 算法進行評分預測分別得到評分矩陣R1[m×n′]、R2[m × n′]和 R3[m × n′]，使用 UIBCF-MF 算法中混合加權方法得到預測結果矩陣R4[m×n′]，添加已提出新用戶數據到預測結果矩陣得到矩陣 R4′′[m × n]，使用MF算法進行二次矩陣分解得到最終預測結果矩陣R4[m × n]。

算法冷啟動解決偽代碼如下。

Begin

輸入 待測數據A，訓練數據B

IF A 中用戶或物品集a∈B 中用戶或物品集b 執行

Step1：將測試數據進行UIBCF-MF 加權混合預測ELSE執行

Step2：提出 A 中滿足 a[i]?b 冷數據

Step3：將提出后的待測數據進行UIBCF-MF 加權混合預測

Step4：添加已提出數據a[i]到預測結果矩陣，使用MF 算法進行評分預測

End

4 結果與分析

4.1 評價標準

實驗使用均方根誤差（rootmeansquareerror，RMSE）和平均絕對誤差（mean absolute error ，MAE）[13-14]作為算法評價指標。計算公式為

4.2 實驗結果

實驗所用數據集為Grouplens 提供的MovieLens數據集中943 位用戶對1 682 部電影的最新評分，共計100 000 條，評分范圍為0~5 分，其中每位用戶至少擁有20 條評分，數據集極其稀疏，稀疏度為0.936 9。實驗將數據集按照8 ∶2 分為訓練集和測試集[15]。

本文設置了3 組對比實驗，第1 組實驗為固定MF 算法所得預測矩陣，當近鄰數Nn 不同時，傳統單一的user-based CF 算法、item-based CF 算法與本文提出的UIBCF-MF 算法的實驗結果對比，user-based CF、item-based 與 UIBCF-MF 的 RMSE 及 MAE 比較分別如圖 1 和圖 2 所示[16]。

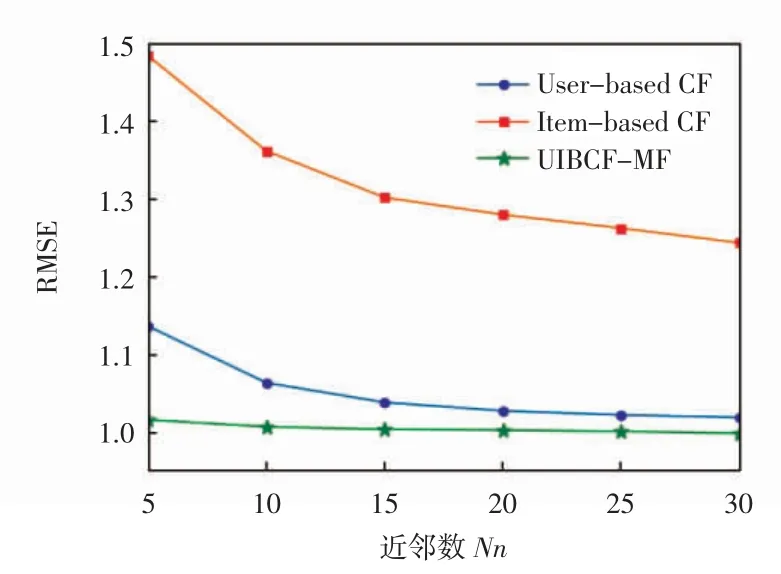
圖 1 user-based CF、item-based 與 UIBCF-MF 的RMSE 比較

圖 2 user-based CF、item-based 與 UIBCF-MF 的MAE 比較

由圖1、圖2 可知，當近鄰數逐漸增大到接近30時，user-based CF、item-based CF 的 RMSE、MAE 值均趨于穩定，而UIBCF-MF 算法受近鄰數影響較小，RMSE、MAE 值隨著近鄰數增大穩定減小，相較單一user-based CF、item-based CF 算法，在利用近鄰用戶或物品進行評分預測的同時，考慮到近鄰用戶或物品較少時會造成推薦不準確，故適當降低該算法比重，提高其他2 種算法權重因子，結果表明UIBCF-MF 算法始終獲得較好的推薦結果。

第2 組實驗為固定user-based CF、item-based CF算法所得預測矩陣，當隱藏矩陣因子不同時，傳統單一的MF 算法與本文提出的UIBCF-MF 算法的實驗結果對比，MF 與 UIBCF-MF 的 RMSE 與 MAE 比較如圖3 所示。

由圖3 可知，隱藏矩陣因子逐漸增大時，MF 所得推薦誤差RMSE、MAE 均增大，而UIBCF-MF 算法受隱藏矩陣因子影響較小，RMSE、MAE 值隨著隱藏矩陣因子增大穩定增大，值為2 時，誤差最小。單一的MF算法解釋性不強，故考慮物品和用戶喜好信息，使得預測評分更加合理準確，結果表明UIBCF-MF 算法始終獲得較好的推薦結果。

圖 3 MF 與 UIBCF-MF 的 RMSE 與 MAE 比較

第3 組實驗為固定user-based CF 算法所得預測矩陣，當近鄰數不同時，文獻[8]中IACF 算法在隱藏因子不同時與本文提出的UIBCF-MF 算法的實驗結果對比，IACF 與 UIBCF-MF 的 RMSE 比較如圖 4 所示，IACF 與 UIBCF-MF 的 MAE 比較如圖 5 所示。

圖 4 IACF 與 UIBCF-MF 的 RMSE 比較

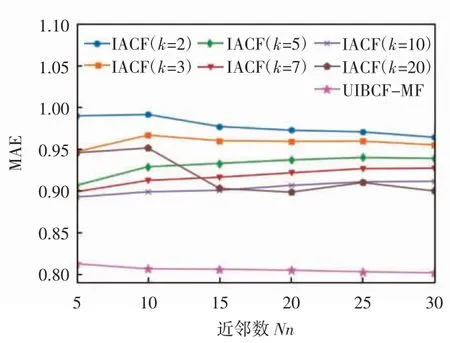
圖 5 IACF 與 UIBCF-MF 的 MAE 比較

由圖4、圖5 可知，隨著近鄰數增大，文獻[8]中IACF 算法RMSE、MAE 值變化較小，本文提出的UIBCF-MF 算法RMSE、MAE 值穩定減小，在隱藏因子不同的情況下，本文提出的UIBCF-MF 算法在item-based CF、MF 算法的基礎上考慮基于用戶的信息，采用匹配度進行度量動態調整權重，對每1 個評分值都考慮到了其用戶和物品特性，并進行權值調整，結果表明UIBCF-MF 算法誤差值遠小于IACF 算法，始終獲得較好的推薦結果。

5 結 語

本文提出了一種基于信息匹配度的混合推薦算法，采用新的評分規范化方法進行評分預測，使得評分數據更為規范，近鄰影響更加合理，結合基于用戶協同過濾、基于物品協同過濾和矩陣分解推薦方法各自的優點，得出某一用戶-物品的預測評分，根據3 種算法與歷史信息匹配度進行動態加權混合求得，不僅數據集稀疏問題得到了解決，也使得推薦結果更加準確并具有可解釋性，使用Grouplens 提供的MovieLens數據集進行實驗，結果表明，相較于傳統的推薦方法，該算法推薦誤差更低，適應性更強，稀疏矩陣中也能取得較好的推薦結果，冷啟動問題得以解決。