基于可分離編碼的高分辨X射線熒光成像技術研究*
孫世峰
1)(華北電力大學核科學與工程學院,北京102206)
2)(華北電力大學非能動核能安全技術北京市重點實驗室,北京102206)
(2020年5月7日收到;2020年6月4日收到修改稿)
1 引 言
基于X射線的分析技術是非常重要的材料表征方法,它們被廣泛用于元素空間分布、化學狀態和質構特性等的測量[1].其中,X射線熒光(XRF)技術因其具有對多元素樣品進行無損分析的能力在許多科學領域和工業應用中得到了迅速發展[1?4].在很多情況下,獲得高質量的X射線圖像非常困難[5].因此,如何提高圖像質量一直是相關學者研究的熱點[6].類似于可見光成像,X射線圖像的質量在很大程度上取決于所采用的光學系統.但是不同于可見光,X射線穿透性強且折射率近似為1,對其進行反射、折射或聚焦都非常困難;用于X射線成像的光學器件,如反射鏡或透鏡等,必須滿足非常嚴格的要求,而且造價非常昂貴[7].
最簡單的實現X射線成像的方法是利用小孔成像原理,設計基于單孔準直器的針孔成像系統.針孔的直徑越小,成像系統的空間分辨率越好;但直徑越小,系統的光收集效率越低,圖像的信噪比(SNR)也越差.為了解決上述問題,Dicke[8]和Ables[9]分別獨立提出了采用多開孔的準直器(編碼孔徑)取代單一開孔的準直器;編碼孔徑技術使系統在保留小孔徑對應的高空間分辨率的同時,大幅提高系統的光收集效率(正比于開孔個數),從而提高圖像信噪比.編碼孔徑技術提出之后得到了極大的發展,并廣泛用于X射線和g射線成像,包括天文觀測、醫學成像和輻射防護等[10?12].
傳統上,X射線熒光成像采用基于全反射原理制成的多毛細管作為光學聚焦器件,但是此類系統能夠收集的X射線的角度范圍過小.為提高系統的數值孔徑,Haboub等[13]探索將編碼孔徑技術用于X射線熒光成像,獲得了幾種標準樣品的實驗圖像,初步驗證了該技術的可行性.Kulow等[14]進一步研究了近場成像時的圖像重建算法,并通過實驗證明了采用編碼孔徑技術可以大幅提高采集到的光子通量,降低成像時間.另外,相比于小孔或多毛細管方案,編碼孔徑技術的一個很重要的優勢是擴展性更強,系統可以在不犧牲分辨率的前提下,通過增加編碼準直器的編碼數和面積,增大成像視野范圍.
目前,編碼孔徑技術應用于X射線熒光成像已顯示出良好應用前景,但仍存在采用傳統的卷積成像模型時,近場成像偽影大、圖像分辨率較低等不足.近年來,得益于計算機視覺算法的進步,編碼孔徑成像技術在光學成像領域取得了一些值得關注的進展.DeWeert[15]和Asif[16]分別提出采用可分離編碼矩陣的編碼孔徑成像模型,可以極大地降低計算的復雜度,從而實現高編碼數下的高分辨成像.基于上述工作,Adams和Boominathan進一步提出了Texas Two-Step(T2S)模型[17],獲得了高幀頻、分辨率達微米級的近場可見光圖像.T2S模型已被證明可用于近場高分辨g射線成像[18].本研究基于可分離編碼的T2S模型,進一步對編碼孔徑技術應用于X射線熒光成像進行詳細的理論分析和模擬計算,期望為將來的實驗研究和實際應用提供參考依據和分析數據.
2 編碼孔徑成像原理
編碼孔徑成像系統通常由編碼準直器和位置靈敏探測器組成,兩者相互平行.編碼準直器為多開孔結構,其上的開孔是按照某種規則排列,開孔部分允許射線通過而非開孔部分阻擋射線.如圖1所示,編碼孔徑成像過程可以分為兩部分:編碼投影和圖像重建.編碼過程即物體發射的射線經過準直器在探測器平面進行投影,對于準直器上的每一個開孔,其均會在探測器平面上產生一個一定比例的物體的倒立投影;編碼孔徑的多開孔,使探測器平面上記錄的是若干倒立投影的退化疊加像.圖像重建即計算機對探測器輸出的原始投影圖像進行圖像解碼,以獲得物體的重建圖像.
假設物體X,探測器測量的投影圖像Y均為M×N的二維矩陣.對于任意的編碼準直器,編碼孔徑成像可以用廣義線性模型表示為

其中,x和y為分別將X和Y的列連接并矢量化后的一維向量(長度為MN);Φ為傳遞矩陣(大小為MN×MN),表示物體和投影圖像之間的線性關系;e是測量噪聲.對于任意給定的編碼準直器和探測器,可以通過模擬射線從物體傳輸到探測器或通過校準過程來獲得不同幾何條件下的傳遞矩陣.但當成像系統分辨率或編碼數較高時,傳遞矩陣Φ將非常大,很難通過估算或校準計算得到Φ,同時,進行圖像重建時的反問題求解也非常困難.比如,當物體圖像和探測器的分辨率均為300×300時,傳遞矩陣Φ將包含(9×104)×(9×104)=8.1×109個元素.
為減少從物體到測量投影的線性映射的復雜性,一般將編碼矩陣設計為可分離的,即二維編碼準直器的圖樣由兩個一維序列的外積構造而來[16,17].此時,可以將式(1)中的成像模型重寫為
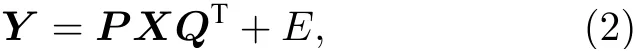
其中,P和Q分別為表示物體行和列的一維卷積的矩陣;E是測量噪聲和模型失配.當物體圖像和探測器的分辨率均為300×300時,P和Q各只有9×104個元素,而Φ中有8.1×109個元素.
在T2 S模型中,考慮到近場效應的影響,探測器投影被進一步分解為兩個可分離函數的疊加[17].對于一個二維的物體Xd,設其距離成像系統的距離為d,探測器的測量投影滿足
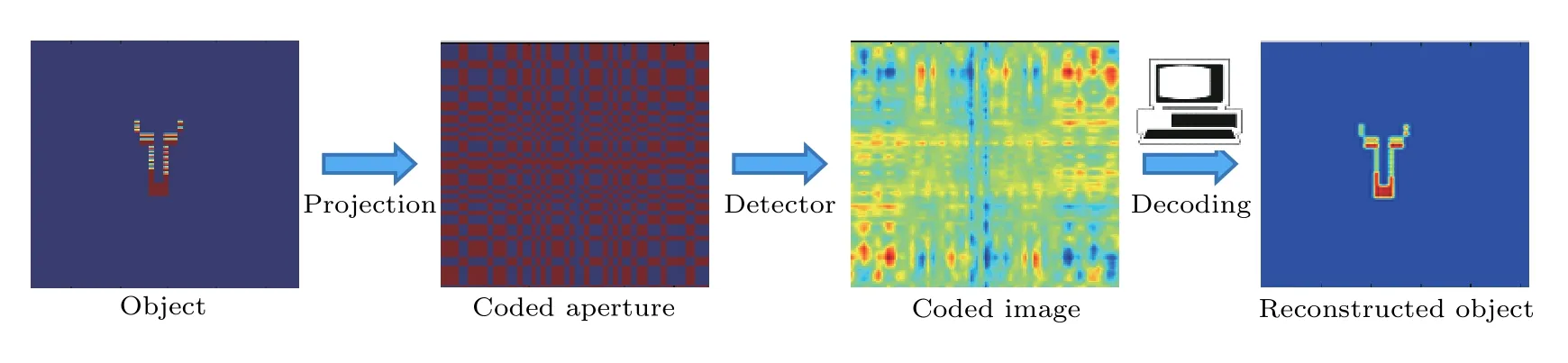
圖1編碼孔徑成像示意圖Fig.1.Schematics diagram of coded aperture imaging.
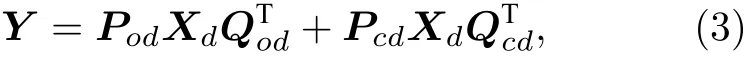
其中,Pod和 Qod為無準直器時探測器響應的傳遞矩陣;Pcd和 Qcd為準直器編碼對應的傳遞矩陣(下標“o”代表開孔,“c”代表編碼,“d”代表不同距離d).
對于三維物體XD,可以將其離散為D個距離成像系統d的二維物體Xd,則測量投影滿足
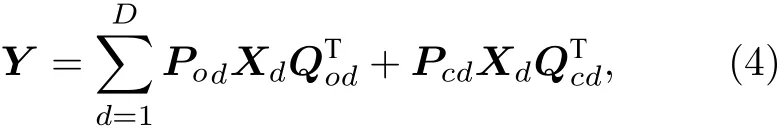
為了減小各種噪聲源項對重建圖像的影響,同時避免過擬合,可以通過求解正則化的總體最小二乘問題來進行圖像重建.采用FISTA(快速迭代閾值收縮算法)[19]求解Lasso問題對應方程,可以得到重建的物體圖像
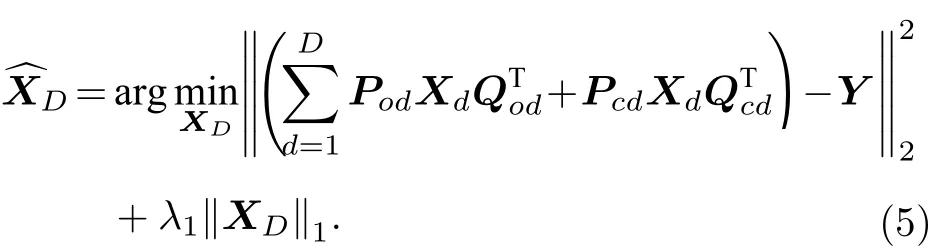
3 基于Geant4的成像模擬
3.1 成像系統參數設計
本工作基于Geant4軟件包[20], 選用QGSP_BIC物理模型,通過設計基于可分離編碼準直器的X射線成像模擬程序,驗證T2S模型用于高分辨X射線成像的有效性.編碼準直器采用修正均勻冗余陣列(modified uniformly redundant arrays,MURA),選擇高編碼數(N=463)以使成像系統具有較高的分辨率.如圖2所示,選取原編碼排布中心區域的90×90個像素設計編碼準直器,黑色部分為重金屬(鉑),白色部分為開孔,單位像素尺寸為25μm×25μm.編碼準直器的厚度應能夠阻擋大部分垂直入射的X射線,考慮到準直效應可能影響重建圖像的質量,準直器厚度設為25—200μm.參考目前pnCCD所用探測器[2],本工作模擬的探測器材料設置為硅, 靈敏體積為2 mm ×2 mm×0.5 mm, 單位像素尺寸為25μm ×25μm,總像素數為80×80.探測器與編碼準直器的距離設置為固定值2 mm.模擬程序記錄入射X射線在探測器上的沉積能量及對應像素編號生成不同情況對應的投影圖像.
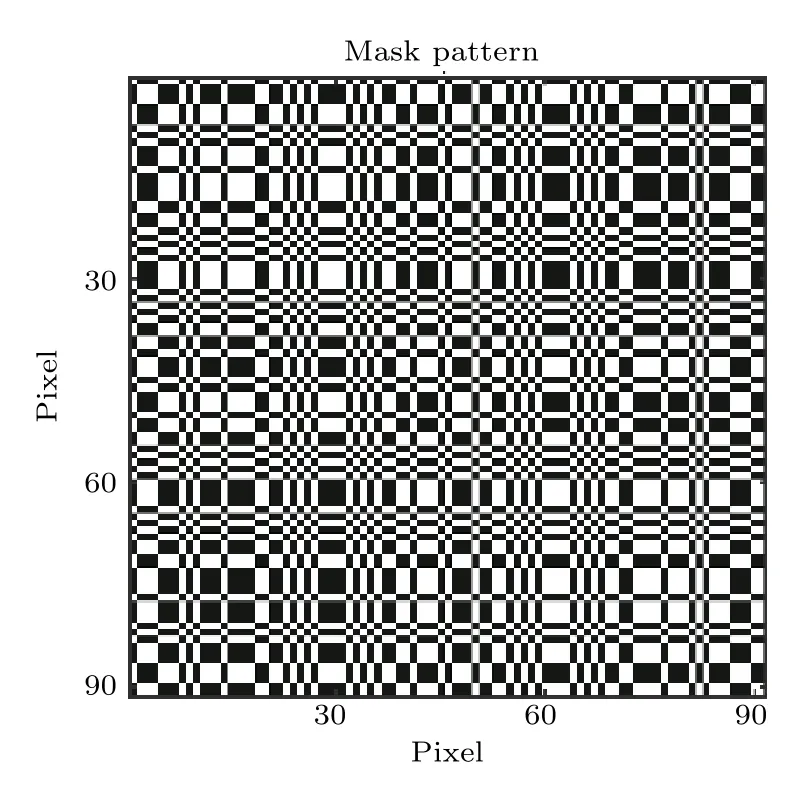
圖2 模擬選用的可編碼準直器圖樣Fig.2.The mask pattern used in the simulation.
3.2 模型校準
對于給定的成像系統,成像模型中的傳遞矩陣可以通過建立射線經準直器到探測器的模型求解或經過校準來得到.本工作通過模擬校準過程,計算所需的所有傳遞矩陣.當物體與系統之間距離固定為任一d時,若物體平面僅第i行對應的像素分布著放射源,即物體圖像可表示為Xi=ei1T.此時探測器測量到的投影圖像為
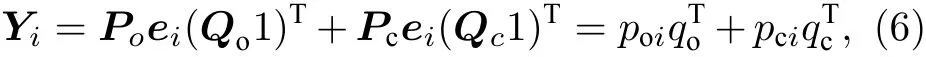
其中,poi和pci分別為Po和Pc的第i列;qo和qc分別為Qo和Qc的列的和.由于poi和pci是正交的,因此可以進行截斷奇異值分解(truncated singular value decomposition,TSVD)投影Yi,僅保留最大的兩個奇異值,分別賦值給poi和pci.通過逐行掃描物體平面的每一行,可以計算出Po和Pc的所有元素.類似地,再通過逐列掃描物體平面的所有列,可以計算出Qo和 Qc的所有元素.通過改變物體與系統之間距離d,重復上述掃描過程,可以獲得不同d對應的傳遞矩陣.
對于上述成像系統,采用長度為2 mm,寬度為0.001 mm的線狀X射線源模擬校準過程.參考相關研究工作[13,14],本文研究的熒光X射線能量范圍設置為5—20 keV,因此計算了線源能量為6、8、10和16 keV時對應的傳遞矩陣.如果系統的參數保持不變,只需執行一次校準過程,對應的傳遞矩陣可重復使用.
3.3 重建圖像評價
本工作主要采用2個二維平面物體測試系統的成像能力. 一是長度為0.4 mm, 寬度為0.001 mm的線源;二是形狀為“180”的物體,考察系統對復雜物體的成像能力.兩個物體均設置在平行于成像系統,且距離為10 mm的平面上.
為了比較不同條件下的重建圖像,選用均方根誤差(root mean square error,RMSE)和通用圖像質量指標(universal quality index,UQI)2個指標定量評價圖像質量.RMSE的定義為:
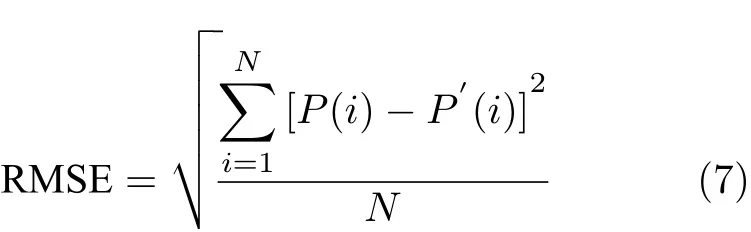
其中,P(i)為原始物體圖像的像素值;P’(i)為重建圖像的像素值;N是圖像總的像素數.RMSE值越大,表明重建圖像與原始圖像的差異越大.
UQI的定義為[21]:
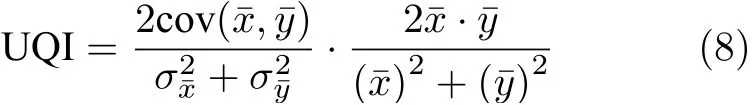
其中,cov是協方差函數;xˉ和yˉ 分別是原始圖像和重建圖像的均值;分別是原始圖像和重建圖像的方差.UQI的動態范圍為[0,1],UQI的值越接近1,表明重建圖像與原始圖像越相似.
4 模擬結果分析
4.1 準直器厚度的影響
采用傳統的卷積成像模型進行近場成像時,由于編碼準直器厚度引起的準直效應會使重建圖像質量嚴重下降[14].因此,本節研究采用T2S模型時,準直器厚度對重建圖像的影響.將X射線能量設置為10 keV,編碼準直器的厚度設置為25、50、100和200μm等4個厚度.圖3(a)所示為0.4 mm線源的重建圖像,由于系統的空間分辨率有限,重建圖像在橫縱向均有一定程度的模糊.雖然線源沿橫向均勻分布,但其重建圖像沿橫向并不是均勻分布,且與準直器厚度無關(圖3b).準直器的厚度從25μm增加到200μm,系統沿縱向的分辨率并無明顯變化(圖3c).通過進一步模擬點源(10 keV)成像, 計算得到準直器的厚度為25、50、100和200 μm時,系統的空間分辨率(半高全寬,FWHM)分別為66.5、65.8、64.9和64.2μm.可以看出,隨著準直器厚度的增加,空間分辨率緩慢減小.作為對比,Haboub等人基于20μm準直器研制的成像系統的空間分辨率約為72μm[13].因此,相比于傳統的卷積模型,采用T2 S模型時分辨率略優.
對于形狀復雜的成像物體,采用T2S模型時,重建圖像比較準確地還原了物體的原始分布情況(圖4b).而采用傳統的卷積模型近場成像時,重建圖像通常存在較強的偽影[13,14].當準直器厚度從25μm增加到200μm,重建圖像無明顯變化.在后兩節的模擬中,準直器的厚度設置為固定值25μm.
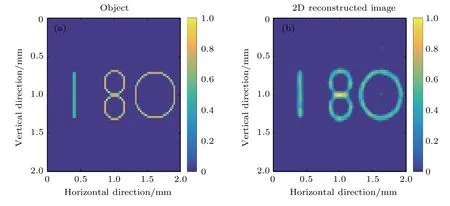
圖4 物體的原始圖像及重建圖像(a)原始圖像;(b)準直器厚度25微米時的重建圖像Fig.4.Original image and reconstructed image of the object:(a)Original image;(b)reconstructed image when the mask thickness was 25 micron.
4.2 X射線能量的影響
X射線的能量越高,穿透能力越強,散射也越嚴重;物體發射的X射線能量不同時,產生的投影圖像不同.同樣,校準時采用的X射線能量不同,計算得到的傳遞矩陣也不同.因此,本節研究物體發射的X射線能量和校準時采用的X射線能量對成像結果的影響.
如圖5所示,當校準能量為10 keV時,物體發射的X射線能量為6和8 keV對應的重建圖像質量較好;而當物體能量增大為16 keV時,重建圖像的質量明顯變差.如圖6所示,當校準能量為16 keV時,物體能量為16 keV對應的重建圖像的質量較好,而物體能量為6和8 keV時,重建圖像均有一定程度的畸變.圖7展示了形狀為“180”的物體的重建圖像質量的定量評價結果隨物體能量和校準能量的變化情況.可以看出,物體能量不同時,不同校準能量對應的重建圖像的質量所能達到的最佳值相近,且均出現在校準能量和物體能量相同時;校準能量和物體能量不同時,重建圖像的質量均有不同程度的變差.整體而言,校準能量為10 keV時,重建圖像質量受物體能量變化的影響最小.
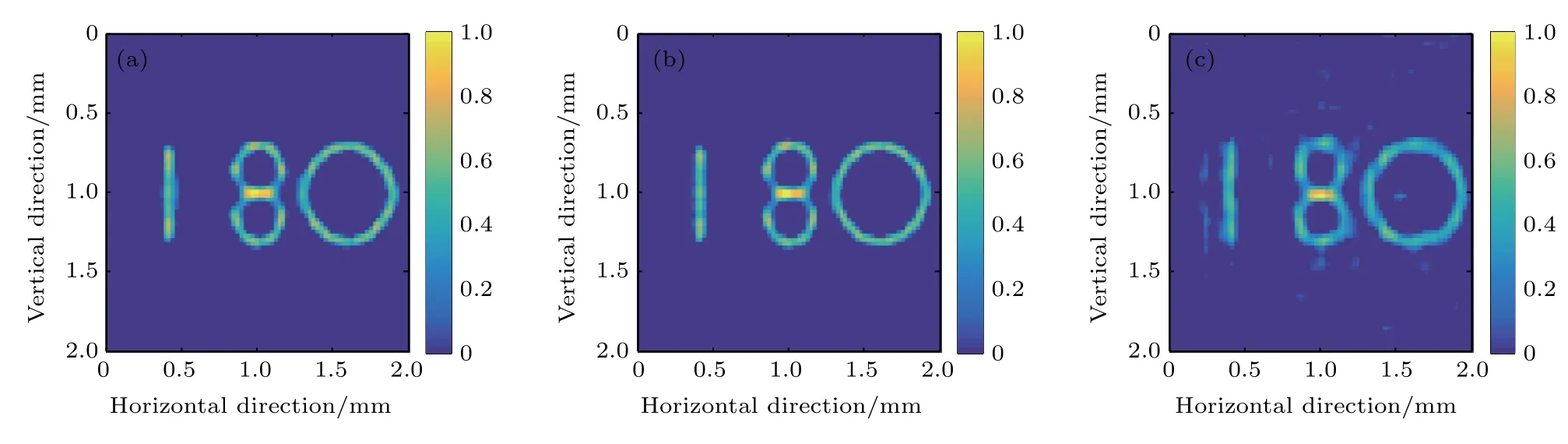
圖5校準能量10 keV情況下物體不同能量時的重建圖像(a)6 keV;(b)8 keV;(c)16 keVFig.5.Reconstructed images of the object with different energies at a calibration energy of 10 keV:(a)6 keV;(b)8 keV;(c)16 keV.
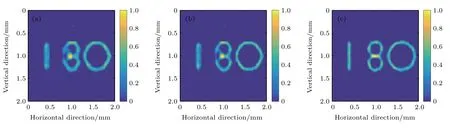
圖6校準能量16 keV情況下物體不同能量時的重建圖像(a)6 keV;(b)8 keV;(c)16 keVFig.6.Reconstructed images of the object with different energies at a calibration energy of 16 keV:(a)6 keV;(b)8 keV;(c)16 keV.
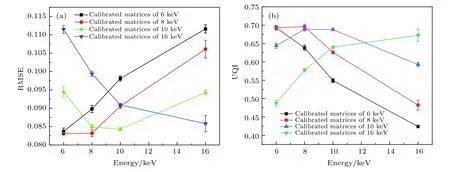
圖7 重建圖像質量的定量評價結果隨物體能量和校準能量的變化情況(a)RMSE;(b)UQIFig.7.Quantitative evaluation results of reconstructed images change with the object energy and calibration energy: (a) RMSE; (b) UQI.
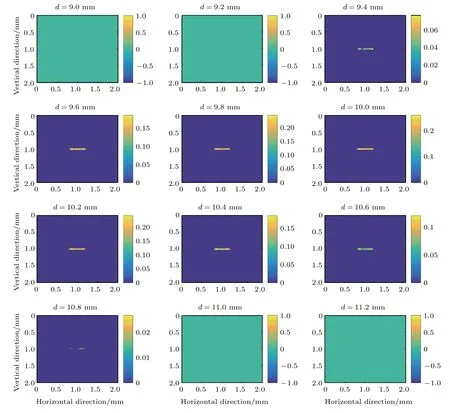
圖8線源的三維重建圖像Fig.8.3D reconstructed image of the line source.
4.3 三維成像結果
在近場條件下,編碼孔徑成像系統可以在二維成像的基礎上提取三維和重聚焦信息.為了考察系統的三維成像能力,將兩個成像物體的能量設為10 keV,并放置于與系統距離為d=10.0 mm的平面上.如圖8所示,雖然模擬的線源是平面物體,但重建的線源出現在不同的軸向切片上,極大值出現在真實距離(d=10.0 mm)附近;成像系統的軸向分辨率較差(FWHM=1.1 mm).圖9是形狀為“180”的物體的三維重建圖像.類似于線源的重建結果,重建物體出現在不同的軸向切片上,并且在真實距離(d=10.0 mm)附近最清晰.因此,相比于傳統基于卷積模型的成像系統僅能實現二維成像,采用T2S模型的成像系統可以很容易地實現距離d的估算.
5 總結與討論

圖9復雜物體的三維重建圖像Fig.9.3D reconstructed image of the complex object.
本文利用Geant4蒙特卡羅仿真,研究了基于可分離編碼的新型編碼孔徑成像計算模型用于高分辨X射線熒光成像的可行性.模擬結果表明,基于該模型的成像系統能夠實現對線源和形狀復雜物體的高質量成像,系統的空間分辨率約為65μm.與采用傳統卷積模型的成像系統不同,該系統的性能在近場成像時并不受準直效應的影響.重建圖像的質量同時受物體能量和校準能量的影響,兩者差異越小,重建圖像的質量越高.系統能夠從單次測量的二維投影圖像,正確地重建出物體與系統的距離,軸向空間分辨率約為1.1 mm.
成像系統的空間分辨率受多個因素的影響,包括編碼準直器和探測器的像素尺寸、物體的放大倍數(取決于物體到編碼準直器的距離與編碼準直器到探測器的距離之比)、圖像重建算法等.提高系統空間分辨率的途徑包括減小編碼準直器和探測器的像素尺寸、增大物體的放大倍數以及采用更復雜的圖像重建算法等.未來的工作將集中于優化系統設計并開發新的重建算法,以進一步提高系統的空間分辨率.

