快速均值回歸隨機波動率模型參數估計及應用

李蓬實, 楊建輝, 林 焰

(1.東莞理工學院 經濟與管理學院,廣東 東莞 523106； 2.華南理工大學 工商管理學院,廣東 廣州 510640； 3.北京大學 匯豐商學院,深圳 100871)

0 引言

傳統的期權定價模型假設波動率是常數, 根據該假設, 不同執行價格的同種標的資產的看漲期權應具有相同的波動率。 然而實證研究表明，從金融市場上的看漲期權價格推算出的波動率在平值期權(at the money)附近的波動率相對較低, 但隨著期權的虛值程度(out of the money)或實值程度(in the money)增加波動率也逐漸增大。 這種現象被稱為隱含波動率的“微笑曲線”(smile)現象。 隱含波動率的“微笑曲線”現象說明了在給定到期期限條件下, 隱含波動率與期權的在值程度或執行價格之間的關系并非固定不變的, 因此傳統的期權定價模型中波動率為常數的假設并不符合現實。 除此之外, 隱含波動率“微笑曲線”還可能是由于標的資產價格的杠桿效應(標的資產價格與波動率之間的負相關關系)與標的資產價格的跳躍現象引起的, 然而傳統的期權定價模型并沒有考慮杠桿效應與資產價格的跳躍現象的存在。

為了解決傳統期權模型中存在的問題, 學者們提出了各種方法來修正傳統期權定價模型的缺陷。 其中兩種主要的模型分別是跳躍擴散模型和隨機波動率模型。 跳躍擴散模型比較適合解決到期期限較短的期權定價問題, 而隨機波動率模型比較適合到期期限較長的期權定價問題。 Bakshi等[1]證明了跳躍擴散模型和隨機波動率模型能夠改進期權定價誤差，同時也發現在考慮隨機波動率之后引入隨機跳躍只能夠有限地減少期權定價誤差。 因此, 本文主要研究隨機波動率模型。

大量實證研究表明金融資產具有隨機波動率的特點。 Chernov等[2]發現金融市場中股票價格的收益率具有明顯的隨機波動率性質。 劉志東等[3]研究了上證50股票指數及其成分股的高頻數據后認為, 中國股市中約43%的風險來源于資產收益過程的隨機波動風險。 通過對中國股市的研究，吳鑫育等[4]認為隨機波動率模型能夠更好地增加模型擬合度。 研究證明標的資產的波動率不僅具有隨機的性質同時具有均值回歸的特點，同時吳鑫育等[5]運用雙杠桿門限隨機波動率模型對中國股市進行實證研究發現，股市具有強波動率持續性以及顯著的杠桿效應。 Liu等[6]通過對臺灣金融市場數據的研究，發現外匯和股指市場中都存在均值回歸的性質。 在實證研究的支撐下, 一般隨機波動率模型假設波動率是由一個具有均值回歸性質的擴散過程驅動。 Hull等[7]首先研究了具有隨機波動率的金融資產的歐式期權定價問題。 Heston[8]假設隨機方差(stochastic variance)服從CIR過程, 通過特征函數的方法推導出歐式看漲和看跌期權的解析解。

Fouque等[9]利用S&P500的數據證實了股指中存在的波動率聚集(volatility clustering)和波動率的快速均值(fast mean-reverting)回歸現象, 在此基礎上他們提出了一種基于快速均值回歸的隨機波動率模型, 該模型在衍生品定價方面得到廣泛的應用。 Fouque等[10]在隨機波動率是快速均值回歸的擴散過程假設下, 利用奇異攝動分析方法推導出歐式看漲期權價格的近似解析解。 Wong等[11]研究了快速均值回歸以及常數彈性波動率假設下渦輪期權(Turbo warrant)的定價問題。 通過引入違約風險中的隨機波動率效應。 Fouque等[12]研究了可違約債券(defaultable bond)的定價問題, 并推導出近似解析解。 Yang等[13]在隨機波動率框架下得到脆弱期權(vulnerable option)的近似解公式, 并研究了隨機波動率對脆弱期權價格的影響。 Kim等[14]考慮了帶有隨機利率的隨機波動率模型, 并證明了在較短的到期期限內新模型的對歐式期權定價效果要優于常數利率模型。

在上述研究成果的基礎上, 本文研究基于快速均值回歸隨機波動率的雙限期權(collar option)定價問題。 雙限期權在到期時間T的收益可以表示為min(max(ST,K1),K2),其中K2>K1>0是期權的執行價格；ST是標的資產在T時刻的價格。 雙限期權可幫助投資者鎖定從投資的標的資產中賺得的利潤, 還可以作為一種對沖策略使投資者避免標的資產價格劇烈變化所引起的投資風險。 除了可以對沖金融產品的風險, 雙限期權還可以用于項目中的收益管理。 Yim等[15]提出將雙限期權用于項目的物料采購, 用雙限期權控制建筑項目中原材料的價格波動。

本文基于快速均值回歸波動率的假設, 同時考慮了標的資產價格過程和驅動波動率擴散過程之間的相關性, 研究雙限期權的定價問題。 由于考慮了波動率的隨機性質, 期權價格難以直接獲得, 因此本文采用Fouque等[10]的方法研究快速均值回歸波動率框架下的期權定價。 該方法優點在于, 首先可以有效地減少隨機波動率模型中的參數；其次可以通過較為簡便的方法對簡化后的模型參數進行估計；最后可以得到期權價格的近似解析解表達式。 本文的主要理論貢獻在于：首先在快速均值回歸隨機波動率框架下研究雙限期權, 由于雙限期權在資產風險管理中的作用, 研究雙限期權的定價問題具有一定現實意義; 其次, 對快速均值回歸隨機波動率模型中的參數進行了估計, 這些參數可以進一步應用到其它期權的定價研究中。

本文共分為五個部分。 第二部分介紹快速均值回歸隨機波動率模型；第三部分給出了基于快速均值回歸隨機波動率模型的參數估計公式；第四部分用金融市場數據估計了模型參數, 推導了考慮隨機波動率的雙限期權定價公式, 同時對雙限期權價格進行了數值分析; 第五部分對本文進行總結。

1 模型

記標的資產在t時刻的價格為St,并假設標的資產滿足以下隨機微分方程

dSt=μStdt+f(Yt)StdWt

(1)

其中μ是標的資產的期望收益率,Wt是標準布朗運動,f(y)是大于零的光滑有界的函數,Yt是一個擴散過程。 與Black-Scholes模型中的常數波動率的假設不同, 式中的波動率是隨機波動率。 假設驅動隨機波動率的擴散過程是一個快速均值回歸的OU過程,Yt滿足以下隨機微分方程

(2)

記為P*風險中性測度,γt為光滑的有界函數，表示波動率風險的市場價格。 根據Girsanov定理, 可得到在風險中性測度下的隨機波動率模型

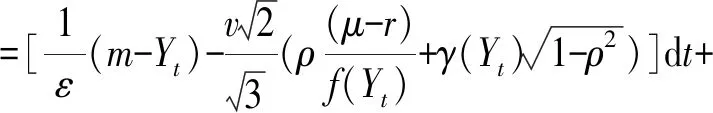
(3)

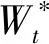
V(t,s,y)=E*[e-r(T-t)φ(ST)|St=s,Yt=y]

(4)

根據Feynman-Kac定理可知, 期權在t時刻的價格V(t,s,y)滿足以下偏微分方程和終值條件

(5)

V(T,s,y)=φ(s)

(6)

將歐式期權在t時刻的價格V(t,s,y)以如下形式展開

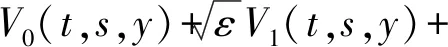
(7)

利用Fouque等[10]提出的奇異攝動方法, 可以由上述偏微分方程和價格展開式得到關于歐式期權價格近似表達式。 由該方法得到的關于歐式期權價格的三個主要結論：

結論1展開式(7)中的第一項與y無關,且V0(t,s)滿足以下偏微分方程和終值條件

(8)

V0(T,s)=φ(s)

(9)

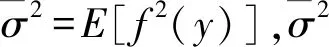
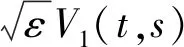
(10)

其中τ是期權合約的到期期限,即τ=T-t；C1和C2是待定系數。

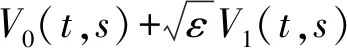
(11)

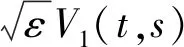
這種方法的優點在于可以有效地減少隨機波動率模型中需要估計的參數的數量。 隨機波動率模型涉及到的模型參數包括波動率擴散過程的均值水平、波動率的方差、波動率的均值回歸速率、模型中兩個隨機過程的相關系數以及波動率風險的市場價格。 利用Fouque等[10]的方法，可以將上述五個模型參數包含到C1和C2兩個系數中。 而C1和C2這兩個系數可以通過金融市場中的看漲期權的隱含波動率的估計值得到。 這兩個參數的估計方法在第3部分介紹。

2 模型參數估計

在給定期權到期時間T和執行價格K的條件下，可以從金融市場上觀測到看漲期權在當前時刻的市場價格。 記該看漲期權的市場價格為Cmarket(K,T)。 所謂隱含波動率(Implied Volatility)指的是使金融市場觀測到的實際期權價格與模型計算得到的理論價格相等的波動率數值。 一般將Black-Scholes期權定價公式作為計算隱含波動率的理論值的基準模型。 記隱含波動率為IV，根據隱含波動率的定義以下關系成立

Cmarket(K,T)=BSC(t,s,IV,K,T)

(12)

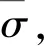
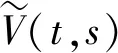
=sN(d1)-Ke-r(T-t)N(d2)+

(13)

其中，

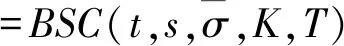
=sN(d1)-Ke-r(T-t)N(d2)

(14)

(15)

(16)

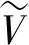
BSC(t,s,IV,K,T)

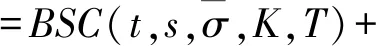
(17)

將式(17)和市場實際價格的近似表達式代入式(12)后, 可知隱含波動率滿足以下關系式

(18)

期權的在值程度(moneyness)指的是期權的實值或虛值程度, 定義為期權執行價格與標的資產價格的比值。 期權的隱含波動率變化可以通過期權的在值程度和期權的到期期限反映出來。 由(18)式能夠進一步推導出隱含波動率IV,期權的在值程度K/s與期權的到期期限τ之間的近似線性關系。

引理1隱含波動率IV,期權的在值程度K/s與期權的到期期限τ滿足以下線性關系。

(19)

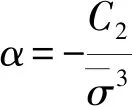
(20)

(21)

根據式(19),可以利用線性回歸方法估計出斜率α和β截距的值, 再利用(20)和(21)推算出C1和C2這兩個參數。

3 實證分析及應用

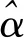
表1 斜率和截距估計值系數

得到斜率和截距的估計值后,可以根據(20)和(21)計算出快速均值回歸隨機波動率模型中的期權定價參數C1和C2:

(22)

(23)

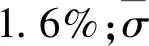
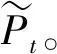
(24)

從(24)可知,雙限期權在到期時刻的價格等價于包含K1單位貨幣，一個多頭頭寸執行價格為K1的看漲期權和一個空頭頭寸執行價格為K2的看漲期權的資產組合。 因此雙限期權在t時刻的價格為

(25)

其中C(Ki)為執行價格為Ki的歐式看漲期權在t時刻的價格。 眾所周知，C(Ki)的表達式為

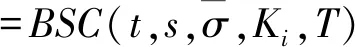
(26)

(27)

由于(25)是兩個歐式看漲期權的線性組合,易知(25)應滿足偏微分方程(8)。因此根據第2部分結論1可知,式(25)式快速均值回歸隨機波動率框架下,歐式雙限期權近似解析解的第一項。在得到近似解析解的第一項之后，可以根據第2部分結論2得到近似解析解的第二項表達式

(28)

在快速均值回歸隨機波動率假設下，雙限期權的價格Pt可以通過(25)和(28)式近似表示，即

(29)

下面通過控制變量的方法進一步分析變量和參數對模型的影響。 取當期標的資產的價格的變動范圍為[200,300],其它參數保持不變。根據式(25)和(29)可以分別得到常數波動率雙限期權價格、隨機波動率雙限期權價格與標的資產價格之間的關系,如圖1所示。根據式(28)可以得到雙限期權近似表達式的修正項與標的資產之間的關系,如圖2所示。

由圖1可以看出,在考慮了隨機波動率之后,雙限期權的價格比常數波動率模型的價格較低。尤其在標的資產價格超過雙期權合約兩個執行價格的均值之后,兩種不同模型給出的價格差異會更加明顯。這個結果說明了,若只通過歷史波動率和Black-Scholes常數波動率模型定價,很可能會高估了雙限期權的價格,從而造成交易損失。由圖2可知,在標的資產變化范圍內，雙限期權近似價格的修正項取值為負數,并且有隨著標的資產價格增加而減少的趨勢。因此考慮了快速回歸隨機波動率的雙限期權價格小于常數波動率模型的價格主要是因為定價公式中的修正項的影響,反映了隨機波動率對期權價格的影響程度。

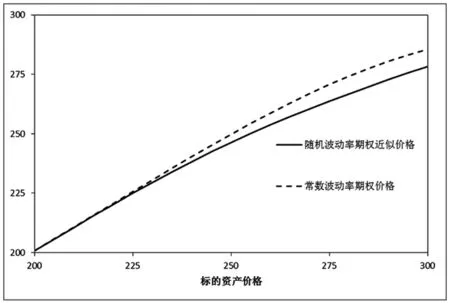
圖1 期權價格比較

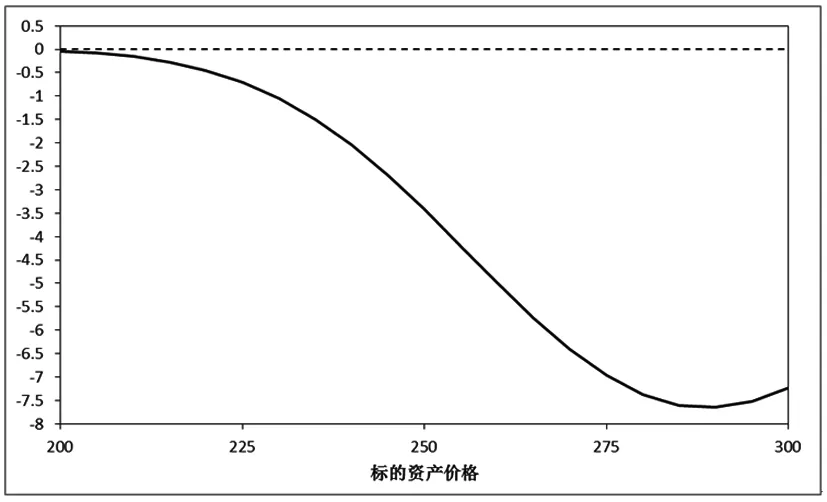
圖2 雙限期權修正項

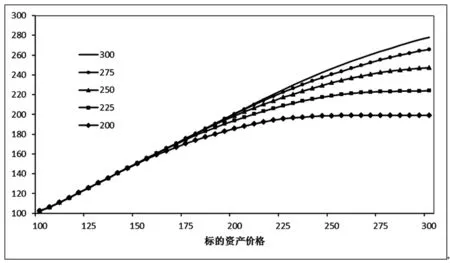
圖3 執行價格對期權價格的影響

取當期標的資產的價格的變動范圍為[100,300],期權執行價格K2的變動范圍為[200,300],其它參數保持不變。根據式(29)可以得到具有不同執行價格的隨機波動率雙限期權價格與標的資產價格之間的關系,如圖3所示。從圖3可知,隨著執行價格K2的增大,隨機波動率雙限期權的價格也較高。這個結論與常數波動率模型的定價是一致的,因此在隨機波動率模型中,執行價格的變化并不會對雙限期權的定價產生影響。

在上述的實證分析和應用中,我們首先利用金融市場上流動性較大的看漲期權的隱含波動率曲線估計出均值回歸隨機波動率模型中的兩個參數,進而應用到雙限期權的定價中。該方法與其它模型相比,具有兩個較為明顯的特點。首先減少了隨機波動率模型(3)中需要估計的參數的個數,提高了效率;其次,可以先從流動性較大的期權(如歐式看漲期權)中估計出求解偏微分方程的參數,再應用到其它流動性較小的期權(雙限期權)定價中,解決了某些奇異期權由于交易數據稀缺無法進行有效參數估計的問題。

4 結論

本文基于快速均值回歸隨機波動率模型,研究了雙限期權的定價問題。雙限期權可以對沖投資者由于標的資產價格波動造成的投資風險,因此研究雙限期權定價問題對于金融市場中的現貨和期權交易,以及金融市場的風險管理和控制具有一定的理論和現實意義。由于傳統的期權定價模型中關于常數波動率的假設無法解釋隱含波動率的“微笑曲線”現象,而快速均值回歸隨機波動率模型不但能夠較好地解釋隱含波動率的“微笑曲線”現象,還能夠較好地解釋標的資產收益的“尖峰厚尾”分布和波動率的“聚集”效應,因此在快速均值回歸隨機波動率模型框架下研究雙限期權定價比較切合實際。本文通過市場隱含波動率的數據,估計了快速均值回歸隨機波動率模型中的兩個參數,并應用到雙限期權的定價計算中。在得到考慮了隨機波動率的雙限期權定價公式之后,對期權價格與標的資產價格之間的關系做了數值分析。基于快速均值回歸隨機波動率模型的期權定價方法可以進一步應用到其它的衍生品定價和資產組合管理中,這也是下一步研究的重要方向。