基于鞍點(diǎn)逼近的投資組合極端風(fēng)險(xiǎn)貢獻(xiàn)度測(cè)度

范 琪， 秦學(xué)志， 王 麟， 宋 宇

(大連理工大學(xué) 經(jīng)濟(jì)管理學(xué)院，遼寧 大連 116024)

0 引言

投資組合風(fēng)險(xiǎn)管理意在通過對(duì)資產(chǎn)的配置以及對(duì)風(fēng)險(xiǎn)的預(yù)警和防范，減少投資組合的潛在損失。在過去幾年我國(guó)金融市場(chǎng)資產(chǎn)價(jià)格高波動(dòng)的背景下，有必要探析投資組合風(fēng)險(xiǎn)波動(dòng)不定的深層次原因。

風(fēng)險(xiǎn)價(jià)值VaR(value at risk)、條件風(fēng)險(xiǎn)價(jià)值CVaR(conditional value at risk) 或期望損失ES(expected shortfall)等是目前廣泛使用的風(fēng)險(xiǎn)度量指標(biāo)。VaR能提供某個(gè)置信度下的可能風(fēng)險(xiǎn)，CVaR或ES能表征超出某個(gè)置信度的可能風(fēng)險(xiǎn)。若需要度量投資組合中每種資產(chǎn)對(duì)組合總風(fēng)險(xiǎn)的貢獻(xiàn)度，則需要對(duì)它們進(jìn)一步改進(jìn)和完善。即通過對(duì)風(fēng)險(xiǎn)指標(biāo)分解，來度量各資產(chǎn)、組合對(duì)總風(fēng)險(xiǎn)的貢獻(xiàn)，藉此用于風(fēng)險(xiǎn)預(yù)警、防范和資產(chǎn)配置等。

將投資組合中每種資產(chǎn)對(duì)總風(fēng)險(xiǎn)的貢獻(xiàn)稱為風(fēng)險(xiǎn)貢獻(xiàn)度。其中常見的定義是資產(chǎn)配置的微小變化對(duì)投資組合總體風(fēng)險(xiǎn)的敏感性(如，Litterman[1], Tasche[2],和Hallerbach[3],。Litterman揭示了風(fēng)險(xiǎn)貢獻(xiàn)度的優(yōu)點(diǎn)并繪制了整體風(fēng)險(xiǎn)來源的幾何形態(tài)，不過他沒進(jìn)一步對(duì)風(fēng)險(xiǎn)貢獻(xiàn)度進(jìn)行分解；Lee和Lam[4],等提出風(fēng)險(xiǎn)貢獻(xiàn)度和風(fēng)險(xiǎn)貢獻(xiàn)比的概念，并實(shí)際應(yīng)用于風(fēng)險(xiǎn)管理和風(fēng)險(xiǎn)預(yù)算以及資產(chǎn)分配與投資組合管理領(lǐng)域；Menchero和Hu[5],提出將風(fēng)險(xiǎn)貢獻(xiàn)度分解為波動(dòng)性和相關(guān)性，但沒進(jìn)一步研究波動(dòng)性和相關(guān)性，也沒將風(fēng)險(xiǎn)貢獻(xiàn)度付諸應(yīng)用；Nil[6],研究了基于風(fēng)險(xiǎn)價(jià)值()的歷史數(shù)據(jù)法表征風(fēng)險(xiǎn)貢獻(xiàn)度，方法雖簡(jiǎn)便，但應(yīng)用于實(shí)際測(cè)算時(shí)存在諸多問題。

值得關(guān)注的是，Martin等[7],通過鞍點(diǎn)估計(jì)測(cè)算了每種資產(chǎn)對(duì)組合的風(fēng)險(xiǎn)貢獻(xiàn)度，并進(jìn)行了實(shí)證研究；在Martin研究基礎(chǔ)上，Muromachi[8],通過假設(shè)投資組合中各資產(chǎn)條件獨(dú)立，提出了一個(gè)新的風(fēng)險(xiǎn)評(píng)估框架，但所計(jì)算出的風(fēng)險(xiǎn)貢獻(xiàn)度準(zhǔn)確性尚不夠高。鑒于上述研究現(xiàn)狀和不足，本文進(jìn)一步優(yōu)化了基于鞍點(diǎn)逼近的風(fēng)險(xiǎn)貢獻(xiàn)度模型。為了驗(yàn)證新方法的有效性，分別采用了鞍點(diǎn)逼近模型和歷史數(shù)據(jù)法對(duì)投資組合的風(fēng)險(xiǎn)貢獻(xiàn)度進(jìn)行了建模和實(shí)證分析。

本文結(jié)構(gòu)如下：首先對(duì)研究現(xiàn)狀進(jìn)行梳理。第一部分對(duì)風(fēng)險(xiǎn)貢獻(xiàn)度的含義進(jìn)行刻畫。第二部分構(gòu)建了基于鞍點(diǎn)逼近的風(fēng)險(xiǎn)貢獻(xiàn)度模型。第三部分采用我國(guó)股票市場(chǎng)股票數(shù)據(jù)，分別基于鞍點(diǎn)逼近模型和歷史數(shù)據(jù)法進(jìn)行了實(shí)證研究，據(jù)此度量了我國(guó)股市的風(fēng)險(xiǎn)。最后得出結(jié)論。

1 風(fēng)險(xiǎn)貢獻(xiàn)度的基本測(cè)度模型

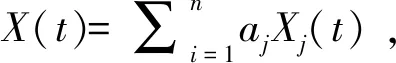
記X為在時(shí)刻T投資組合收益率的隨機(jī)變量，以FX(x)表示其分布函數(shù)，fx(x)表示其密度函數(shù)。本文中，X的100α分位數(shù)表示為Qx(α),0<α<1, 則

QX(α)=inf{x|Fx(x)≥α}

(1)

如果FX(x)是關(guān)于x的嚴(yán)格遞增函數(shù)，則QX(α)=x,其中滿足Fx(x)=α。

記c是參考值，如c為投資組合t時(shí)刻的平均收益率，則VaR在置信水平α下可定義為

VaRX(α)=c-QX(1-α)

(2)

以RCj表示資產(chǎn)j在投資組合中的風(fēng)險(xiǎn)貢獻(xiàn)度，定義如下：投資組合總風(fēng)險(xiǎn)Rp相對(duì)于aj的微小變化的敏感性?RP/?aj，再乘以aj，即

(3)

其中，RP可以是標(biāo)準(zhǔn)差、VaR或CVaR等。

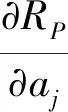
(4)

Tasche對(duì)采用來表征風(fēng)險(xiǎn)貢獻(xiàn)度的必要條件進(jìn)行了推證，即，如果資產(chǎn)j在置信度α下的VaR風(fēng)險(xiǎn)貢獻(xiàn)度存在，可表示如下:

(5)

遺憾的是，式(5)很難給出解析解，為此現(xiàn)有研究廣泛采用歷史數(shù)據(jù)法: 假設(shè)未來的收益分布依賴過去時(shí)期的收益分布，即通過歷史收益來估計(jì)組合的未來潛在收益分布及風(fēng)險(xiǎn)大小，進(jìn)而求出相應(yīng)的風(fēng)險(xiǎn)貢獻(xiàn)度。

上述方法存在一定的局限。歷史數(shù)據(jù)法主要適用于存在數(shù)據(jù)量較大且持有期較短的情況，但是即使持有期短、觀測(cè)數(shù)據(jù)很多，對(duì)風(fēng)險(xiǎn)價(jià)值和極端情況下的風(fēng)險(xiǎn)貢獻(xiàn)度的估計(jì)仍由處于分布尾部相對(duì)少量的觀測(cè)值決定，因此估計(jì)的準(zhǔn)確性仍難以保證。

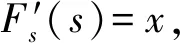
2 鞍點(diǎn)逼近模型

2.1 對(duì)一般分布函數(shù)和密度函數(shù)的估計(jì)

假設(shè)投資組合中單個(gè)資產(chǎn)的收益率服從獨(dú)立同分布。對(duì)于資產(chǎn)j的收益率采用鞍點(diǎn)逼近方法，得到投資組合收益率的密度函數(shù)和分布函數(shù)近似表示。

Xj(t)的矩母函數(shù)MXj(s)可表示為

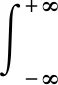
(6)

投資組合收益率X(T)的矩母函數(shù)可表示為

(7)

根據(jù)定義，投資組合收益率X(T)的生成函數(shù)為

KX(s)=logMX(s)

(8)

通過Fourier逆變換，投資組合密度函數(shù)可表示為

(9)

其中γ為一個(gè)趨于無窮小的實(shí)數(shù)。因此，為了便于計(jì)算，本文使用鞍點(diǎn)逼近方法。通過鞍點(diǎn)估計(jì)[11]，可得

(10)

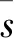
通過使用Edgeworth展開公式漸進(jìn)展開，得到關(guān)于投資組合收益率的分布函數(shù)估計(jì)[12]:

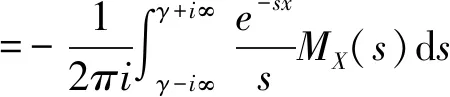
(11)

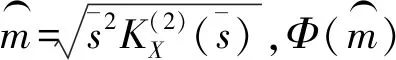
2.2 對(duì)投資組合風(fēng)險(xiǎn)貢獻(xiàn)度的表示

若FX(x)對(duì)aj可微的，則

(12)

進(jìn)而得到：

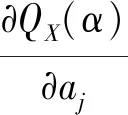
(13)

c是參考值，如果c對(duì)aj可微的，根據(jù)式(13)可以得到投資組合中資產(chǎn)j風(fēng)險(xiǎn)貢獻(xiàn)度表達(dá)式：

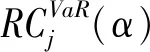
(14)

3 實(shí)證研究

3.1 投資組合VaR及風(fēng)險(xiǎn)貢獻(xiàn)度的計(jì)算

2012年8月，為反映房地產(chǎn)行業(yè)股票的收益表現(xiàn)，向市場(chǎng)提供細(xì)分的行業(yè)投資標(biāo)的，國(guó)證房地產(chǎn)指數(shù)以巨潮行業(yè)分類標(biāo)準(zhǔn)為基礎(chǔ)，選取A股市場(chǎng)上歸屬于房地產(chǎn)行業(yè)的規(guī)模和流動(dòng)性突出的50只股票作為樣本股。查詢從2014年1月至2016年3月國(guó)證房地產(chǎn)指數(shù)數(shù)據(jù)，萬(wàn)科A(15.684%)、保利地產(chǎn)(7.719%)和招商蛇口(4.956%)三支股票在國(guó)證房地產(chǎn)指數(shù)中一直占很高權(quán)重。從國(guó)證房地產(chǎn)指數(shù)選取權(quán)重可知，這三支股票對(duì)房地產(chǎn)行業(yè)具有一定的代表性。

因此，本文選擇上述三支股票，使用鞍點(diǎn)逼近模型和歷史數(shù)據(jù)法測(cè)算投資組合的和對(duì)應(yīng)的風(fēng)險(xiǎn)貢獻(xiàn)度，并與實(shí)際結(jié)果比較。

假設(shè)所選三支股票組成一個(gè)投資組合，組合中三支股票所占比例與單只股票市值有關(guān)，即為單支股票的年均市值。招商地產(chǎn)在2015年4月3日因宣布“籌劃重大事項(xiàng)”而停牌，同時(shí)萬(wàn)科A股在2015年12月份因被惡意收購(gòu)而停牌。所以本文選擇對(duì)2015年4月2日的數(shù)據(jù)進(jìn)行估計(jì)。同時(shí)，因股票一年的交易日是250天，所以本文使用2014年3月25日至2015年4月1日共250個(gè)數(shù)據(jù)作為分析基礎(chǔ)。使用鞍點(diǎn)逼近模型和歷史數(shù)據(jù)法測(cè)算2015年4月2日三支股票所組成投資組合所對(duì)應(yīng)的及風(fēng)險(xiǎn)貢獻(xiàn)度，并與2015年4月2日三支股票所組成投資組合的對(duì)應(yīng)結(jié)果進(jìn)行比較，得出最適用模型。

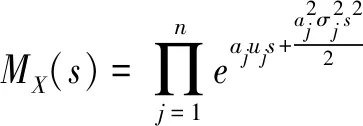
表1列出了2015年4月2日兩種方法三種置信度下所測(cè)算投資組合的VaR和對(duì)應(yīng)風(fēng)險(xiǎn)貢獻(xiàn)度的結(jié)果，從中可以看出，所有模型測(cè)算的VaR都大于真實(shí)值，可知所有模型都不會(huì)低估風(fēng)險(xiǎn)。所以，如果歷史數(shù)據(jù)缺乏，可使用鞍點(diǎn)逼近模型計(jì)算投資組合風(fēng)險(xiǎn)價(jià)值VaR，這對(duì)極端風(fēng)險(xiǎn)的識(shí)別與謹(jǐn)慎規(guī)避具有重要意義。表2列出了兩種方法三種置信度下每種資產(chǎn)的風(fēng)險(xiǎn)貢獻(xiàn)度測(cè)算情況與實(shí)際情形比較(偏差)，并計(jì)算了整個(gè)投資組合偏差。由表2可知：除外α=95%，鞍點(diǎn)逼近法的精度大于歷史數(shù)據(jù)法的精度，若進(jìn)一步考慮歷史數(shù)據(jù)缺乏或很難獲取情況下鞍點(diǎn)逼近模型的優(yōu)異表現(xiàn)，可以認(rèn)為鞍點(diǎn)逼近模型測(cè)算結(jié)果具有較強(qiáng)的代表性。同時(shí)比較α三種取值下投資組合VaR值和投資組合風(fēng)險(xiǎn)貢獻(xiàn)度偏差可知，當(dāng)α=95%時(shí)，無論是鞍點(diǎn)逼近法或者歷史數(shù)據(jù)法，所得結(jié)果都最可靠。

表1 2015年4月2日風(fēng)險(xiǎn)貢獻(xiàn)度和VaR的估計(jì)值

表2 估計(jì)結(jié)果與實(shí)際值的精度比較

3.2 基于歷史情景法的壓力測(cè)試

上述實(shí)證分析日期為2015年4月2日，當(dāng)日上證綜指的漲跌幅是0.41%，國(guó)證房地產(chǎn)指數(shù)的漲跌幅是-0.45%，屬輕微震蕩。但是，20多年來我國(guó)股市歷經(jīng)多次大震蕩大調(diào)整。特別是2015年，滬指暴跌42.7%，各方損失慘重。因此對(duì)極端情況下鞍點(diǎn)逼近模型可靠性分析極為重要。本文測(cè)試了上證綜指和國(guó)證房地產(chǎn)指數(shù)出現(xiàn)極端暴跌情況下投資組合的VaR和風(fēng)險(xiǎn)貢獻(xiàn)度。

對(duì)漲跌幅的選擇：分別收集上證綜指和國(guó)證房地產(chǎn)指數(shù)2012年8月至2015年12月漲跌幅數(shù)據(jù)進(jìn)行排序分析，考慮投資組合三類資產(chǎn)數(shù)據(jù)的有效性，選擇此時(shí)間段內(nèi)上證綜指最大跌幅8.49%和國(guó)證房地產(chǎn)最大跌幅8.75%為極端情景,進(jìn)行壓力測(cè)試。

表3列出了在上證綜指和國(guó)證房地產(chǎn)指數(shù)出現(xiàn)極端跌幅下投資組合的實(shí)際損失值和風(fēng)險(xiǎn)貢獻(xiàn)度以及鞍點(diǎn)逼近模型在三種α置信水平下所測(cè)算出投資組合的VaR和風(fēng)險(xiǎn)貢獻(xiàn)度。比較投資組合VaR值可知，即使在極端情況下，模型所測(cè)出的VaR也不會(huì)出現(xiàn)低估情況。表4列出鞍點(diǎn)逼近模型三種置信度下每種資產(chǎn)風(fēng)險(xiǎn)貢獻(xiàn)度測(cè)算情況與實(shí)際情形的偏差，并計(jì)算了投資組合的偏差。通過投資組合偏差可知：當(dāng)上證綜指和國(guó)證地產(chǎn)指數(shù)出現(xiàn)劇烈震蕩時(shí)，鞍點(diǎn)逼近模型所計(jì)算結(jié)果偏差小于10%，應(yīng)屬合理誤差范圍內(nèi)。且當(dāng)置信度α=95%時(shí)，所得結(jié)果相對(duì)實(shí)際值偏差最小。同時(shí)，投資組合偏差程度隨α置信度增加而增加。所以，在極端情況下鞍點(diǎn)逼近模型也能較好地測(cè)算投資組合風(fēng)險(xiǎn)貢獻(xiàn)度。

表3 鞍點(diǎn)逼近模型在上證指數(shù)和國(guó)證指數(shù)極端跌幅下的測(cè)算結(jié)果

表4 極端情景下上證指數(shù)和國(guó)證指數(shù)鞍點(diǎn)逼近模型測(cè)算精度

4 結(jié)論

決策者若能對(duì)所擁有的投資組合風(fēng)險(xiǎn)貢獻(xiàn)度進(jìn)行定量分析，就有望得到具有前瞻性的風(fēng)險(xiǎn)貢獻(xiàn)度信息，這有助于決策者在負(fù)面結(jié)果出現(xiàn)之前，通過及時(shí)調(diào)整投資組合等策略，減少未預(yù)期風(fēng)險(xiǎn)帶來的損害，因?yàn)轱L(fēng)險(xiǎn)貢獻(xiàn)度度量了個(gè)體資產(chǎn)的風(fēng)險(xiǎn)對(duì)整個(gè)組合資產(chǎn)風(fēng)險(xiǎn)的貢獻(xiàn)，是投資組合管理者藉此做出科學(xué)資產(chǎn)配置的重要依據(jù)之一。

本文給出基于鞍點(diǎn)逼近模型計(jì)算投資組合風(fēng)險(xiǎn)貢獻(xiàn)度的方法。通過鞍點(diǎn)逼近模型，能估計(jì)出簡(jiǎn)潔的投資組合密度函數(shù)和分布函數(shù)。同時(shí)，實(shí)證研究結(jié)果表明，鞍點(diǎn)逼近模型所計(jì)算出的結(jié)果在多數(shù)情況下其精度高于歷史數(shù)據(jù)法，若進(jìn)一步考慮歷史數(shù)據(jù)缺失(例如股票停牌等)頻繁出現(xiàn)的現(xiàn)實(shí)背景，采用鞍點(diǎn)逼近法測(cè)算投資組合風(fēng)險(xiǎn)貢獻(xiàn)度的實(shí)用性將更加凸顯，壓力測(cè)試分析也支持了在極端情況下鞍點(diǎn)逼近模型的適用性。

最后，需要指出的是，因本身的局限性，所計(jì)算的風(fēng)險(xiǎn)貢獻(xiàn)度精度仍有通過其他度量方法進(jìn)一步提高的可能，這有待進(jìn)一步研究。