圖解法和矩值法海洋沉積物粒度參數的對比

李高聰，李志強，朱士兵，張會領，曾春華

圖解法和矩值法海洋沉積物粒度參數的對比

李高聰1，李志強1，朱士兵1，張會領2，曾春華2

（廣東海洋大學：1. 電子與信息工程學院//2. 海洋工程學院，廣東 湛江 524088）

【】系統探討圖解法和矩值法計算海洋沉積物粒度參數結果的相互轉換關系。首先對雷州半島南三島海灘沉積物開展圖解法和矩值法粒度參數的對比研究，然后將結果與其他分析結果相結合，討論兩種方法在不同沉積環境中的轉換規律。對于南三島海灘樣品而言，兩類方法獲得的平均粒徑和分選系數相關性較高（2≥ 0.821），可相互轉換，但偏態和峰態的相關性較弱（2≤ 0.229），不存在相互換算的數學基礎；對于不同沉積環境的樣品而言，兩類方法的計算結果不存在隨計算公式階次增加而相關性逐漸變差的普適規律；兩類方法所得的平均粒徑和分選系數可相互換算，但偏態和峰態在不同沉積環境中的可換算性差異較大。圖解法和矩值法計算的粒度參數在不同沉積環境存在較大差異，不能直接相互替代。

粒度參數；圖解法；矩值法；相互換算關系；不同沉積環境

對沉積物進行粒度分析是獲取沉積環境的物質來源、物質輸運趨勢、污染物濃度和沉積環境類別分析等有關信息的重要步驟[1-7]。沉積物粒度分布特征通常使用粒度參數來定量表征。常見粒度參數一般包括4種，即平均粒徑、分選系數、偏態和峰態。這些參數分別代表了沉積物顆粒的粗細、均勻性、對稱性和相對集中程度，主要受物源顆粒的原始大小和搬運介質的平均動能影響[1-2, 8-9]。計算粒度參數的方法有很多，目前被廣泛使用的可分為圖解法和矩值法兩大類。圖解法是基于粒度分析結果繪制出頻率累積曲線圖，隨后在曲線上選擇幾個具有代表性的點，利用簡單計算公式求得粒徑參數結果[1-2]。矩值法則將平均粒徑值、分選系數值、偏態值和峰態值分別定義為粒度分布的一、二、三和四階矩函數[8-9]。

在眾多的圖解法公式中，Folk & Ward圖解法計算的粒度參數具有明確的物理意義，應用最為廣泛[10-11]。為尋求Folk &Ward圖解法和不同矩值法計算得到的粒度參數之間的聯系和可比對性，急需開展對不同沉積物環境的沉積物樣品關于兩類方法計算結果的對比研究。目前，已有眾多研究者開展了大陸坡[12]、深海盆地[12]、河口海岸[13]、潟湖[14]、海灣[15]、河口近海[16]和潮灘環境[17]的沉積物樣品關于圖解法和矩值法計算結果的對比分析，尚還少見對海灘沉積環境的研究報道。為此，本研究利用雷州半島東北部南三島海灘的109個沉積物樣品開展海灘沉積環境的案例分析。在此基礎上，將結果與上述不同沉積環境的研究案例匯總起來，綜合探討圖解法和矩值法計算得到的粒度參數之間的關系。本研究有助于提高對不同沉積環境粒度參數關于不同計算方法之間的異同及其原因的認知水平，進而可為未來特定沉積環境粒度參數計算方法的選擇提供決策參考。

1 材料與方法

粒度分析樣品來自雷州半島東北部南三島采樣區域受人類活動影響較小的海灘岸段，總長度1.1 km（圖1）。采樣時間為2018年8月14日低潮位時段，沉積物樣品包含了潮上帶、潮間帶和潮下帶共109個表層沉積物樣品。采樣間隔在沿岸方向上，每隔100 m采集1個樣品；在離岸方向上，每隔10 m采集1個樣品。實驗室樣品預處理及分析流程按照《海洋底質調查技術規程》[13]。首先，取適量樣品加入燒杯中，并使用質量濃度為10%的鹽酸去除樣品中的碳酸鈣物質；其次，加入雙氧水靜置12 h以上，去除樣品中有機質；隨后，加入蒸餾水，稀釋過量的鹽酸和雙氧水，靜置24 h以上，并抽掉上部澄清液體；然后，加入0.5 mol/L的六偏磷酸鈉溶液，并用超聲波振蕩10 min來分散樣品；最后，將處理好的樣品倒入BT-2002激光粒度儀測量粒度。BT-2002激光粒度儀的測量范圍為1~2 600 μm，重復性誤差小于3%。

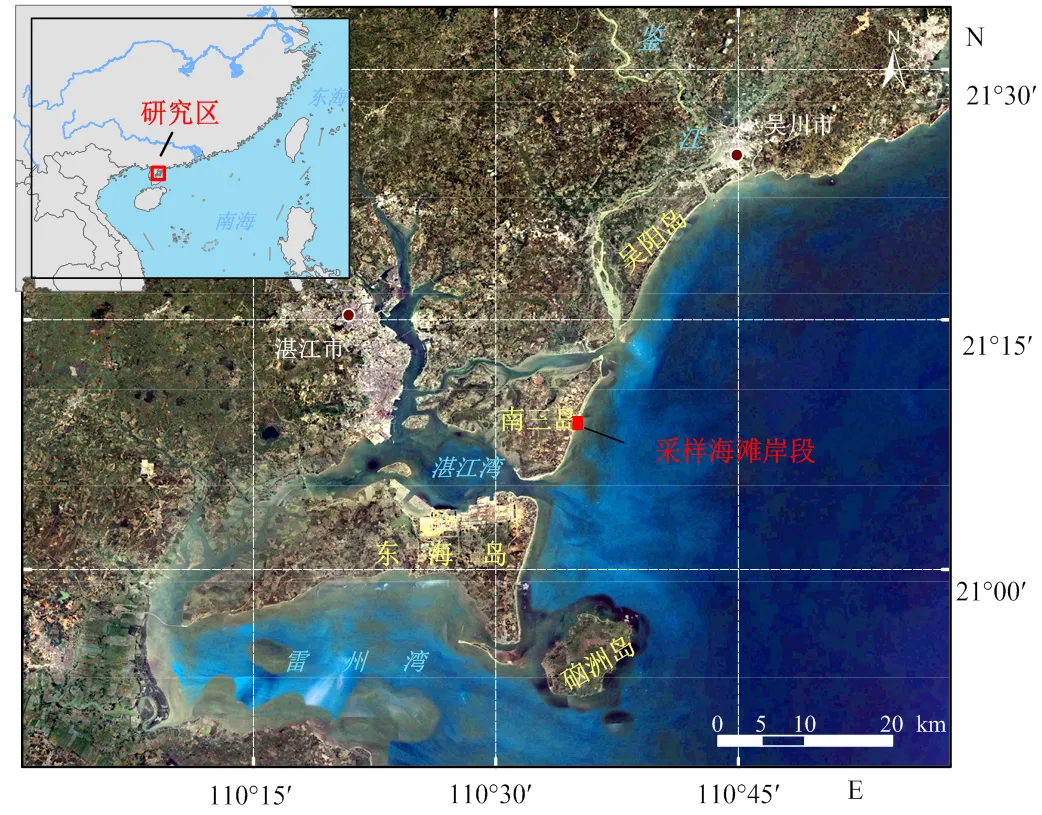
圖1 研究區位置

本研究探討的沉積物粒度參數包括平均粒徑、分選系數、偏態和峰態等4類。首先，基于MATLAB的線性內插功能，獲取5、1625507584、95和粒級組的中值（X）。其次，利用表1中3種公式，即Folk & Ward的圖解法[1]、Friedman的矩值法[3]和McManus的矩值法[4]，進行粒度參數計算。隨后，通過線性回歸分析和作圖法評估3種計算方法所得粒度參數結果的相關性。在計算時，由于兩種矩值法的平均粒徑和分選系數計算公式一致，只對圖解法和矩值法的結果進行一次回歸分析處理。

表1 沉積物粒度參數計算公式匯總

注：5、162550758495分別對應概率累積曲線上5%、16%、25%、50%、75%、84%和95%的粒徑（）；X為粒級組的中值（），f為各粒級范圍的百分比含量。

2 結果

2.1 沉積物平均粒徑

結果表明，圖解法和矩值法計算的平均粒徑數值幾乎全部都落在了直線=上（圖2a）。線性回歸分析表明，圖解法和矩值法線性回歸的擬合優度達到了0.98（表2），表明兩類方法計算的平均粒徑數值非常接近，能夠相互代替。

表2 圖解法與矩值法粒度參數的相關關系統計

2.2 分選系數

相較于平均粒徑分布情況，圖解法和矩值法計算的分選系數要相對離散一些，但也基本圍繞直線分布（圖2b）。矩值法計算得到的分選系數略大于圖解法計算的結果。兩類方法計算結果的擬合優度也較高，達到0.82（表3）。因此，兩類方法計算的分選系數可以通過線性關系相互換算。

2.3 偏態

從圖2c和2d可以看出，圖解法和矩值法計算的偏態值在分布上明顯偏離直線。總體而言，圖解法計算的結果大于MMFr矩值法計算的結果，但其值比MMMc矩值法計算的結果明顯要小。兩類方法計算的結果之間缺少線性相關趨勢，線性擬合優度數值很小，數值僅為0.23和0.07（表3）。因此，圖解法和矩值法計算的偏態不能通過線性關系相互換算。

2.4 峰態

與偏態類似，圖解法和矩值法計算的峰態值在分布上顯著偏離直線=（圖2e、2f）。在數值大小上，圖解法計算結果明顯小于MMFr矩值法計算結果，但其數值要大于MMMc矩值法計算值。同樣，兩類方法計算值之間缺少線性相關趨勢，線性擬合優度數值僅為0.03和0.16（表3）。因此，圖解法和矩值法計算的峰態也不能通過線性關系來相互替換。

3 討論

Folk & Ward圖解法[1]和Friedman矩值法[9]或McManus矩值法[9]是計算沉積物粒度參數最常用的方法[8-21]。兩類方法共同之處在于存在一個相同假設，即沉積物粒度分布服從對數的正態分布。不同之處在于圖解法僅考慮了90%主要粒級分布情況，而矩值法則考慮了全部粒級分布情況[1-2, 8-9]。可以推論，兩類方法計算結果的異同是受檢沉積物的粒度分布偏離對數正態分布以及尾部10%粒級分布情況的函數。如果受檢沉積物的粒級分布嚴格符合對數正態分布，這兩類方法的計算結果應該完全一致。如果受檢沉積物的粒級分布偏離了對數正態分布，則會產生偏差，且偏差程度會隨著計算公式階次的增加而發生顯著變化。

為探討兩類方法計算粒度參數結果的偏差情況，需對盡可能多類型的沉積物樣品或對不同沉積環境的沉積物樣品進行對比分析。基于此，本研究匯總了眾多研究者在不同海洋沉積環境中采集的沉積物樣品關于矩值法和圖解法粒度參數之間的對比分析結果（表3）。結果表明，在大陸坡、深海盆地、河口海岸、堡島-潟湖、海灣、河口近海和潮灘沉積環境中，圖解法和矩值法計算的平均粒徑具有非常好的線性相關關系，它們的線性回歸擬合優度都大于等于0.940。分選系數情況與此類似，也顯示出較高線性相關關系，線性回歸擬合優度大多數都大于等于0.940。上述平均粒徑和分選系數的情況與本研究基于南三島地區海灘表層沉積物樣品的結果是一致的，表明這一結論具有一定普適性。

但對于偏態和峰態而言，不同沉積環境下圖解法和矩值法結果的相關性存在較大差異。在大陸坡、深海盆地和潮灘環境，兩類方法計算的偏態和峰態存在較好線性回歸關系，它們擬合優度的范圍達到了0.669 ~ 0.937。然而，在河口海岸、海灣和本研究的海灘沉積環境中，兩類方法計算的偏態和峰態線性關系較弱，擬合優度值僅為0.035 ~ 0.229。從計算公式差異可知，當物質組成均勻和頻率分布接近正態分布時，兩類方法的粒度參數的相關性會比較高[10-18]。但當沉積物較粗或較細時，由于粒度分布偏離正態分布，且具有明顯的尾部特征，兩類方法的計算結果差異會隨之增大[10-21]。因此，無論在什么沉積環境中，圖解法和矩值法計算的平均粒徑和分選系數都會存在明確的線性可轉換關系，但是對于偏態和峰態而言，線性轉換關系僅存在于少數幾個沉積環境。

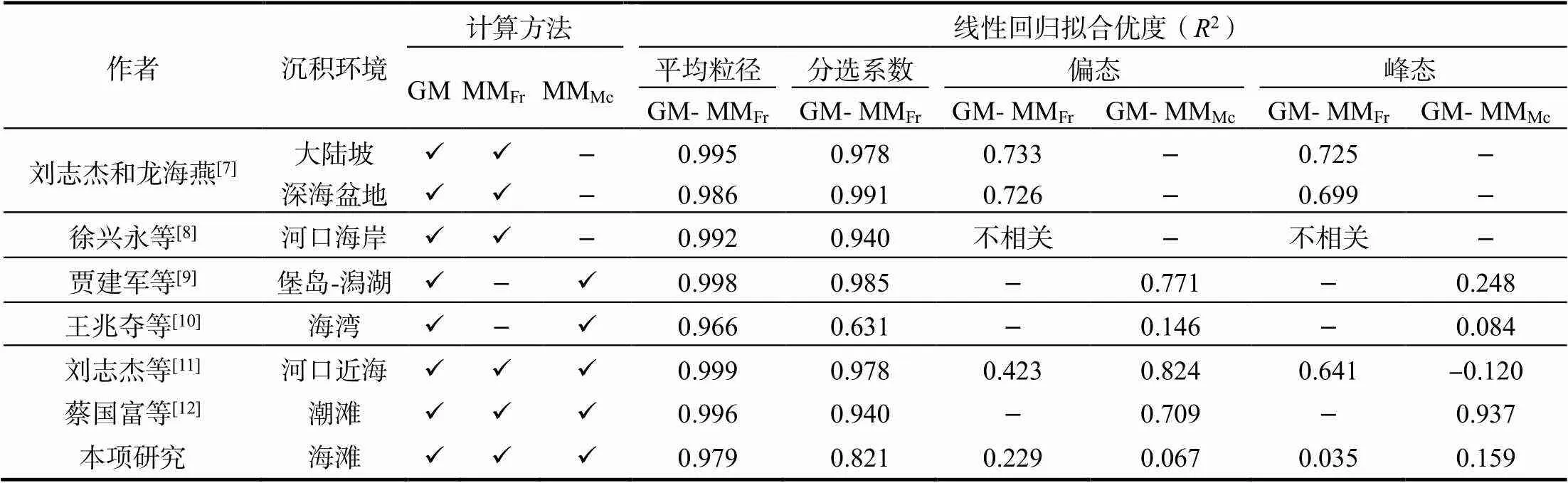
表3 粒度參數不同計算方法的相關性分析結果匯總

為使粒度參數結果便于對比，Folk & Ward[1]根據統計學原理提出基于圖解法粒度參數數值結果對應的定性描述術語（表4）。在理論上，當4個粒徑參數相關性都較高的情況下，圖解法和矩值法結果可以相互轉換。基于此，有不少學者利用圖解法和矩值法粒度參數的線性轉換關系，推導出矩值法粒度參數數值對應的定性描述術語參照表（如表5和表6）[14, 17, 20]。通過對比表5和表6可知，對于偏態和峰態兩個參數的描述術語而言，相同術語對應的數值范圍是不一致的。其原因在于表5是建立在潮灘沉積環境，而表6是建立在堡島-潟湖沉積環境，兩個環境在物源供給和水動力條件方面存在明顯差異。因此，表5和表6 推算出的矩值法定性描述術語僅適用于各自所在研究區（類似于建立了地方參照標準），而不具有普適性。而對于粒徑參數相關性較差的研究區而言，圖解法和矩值法數值結果不存在相互換算的數學基礎，也就不存在傳遞特定物理指示意義的可能。

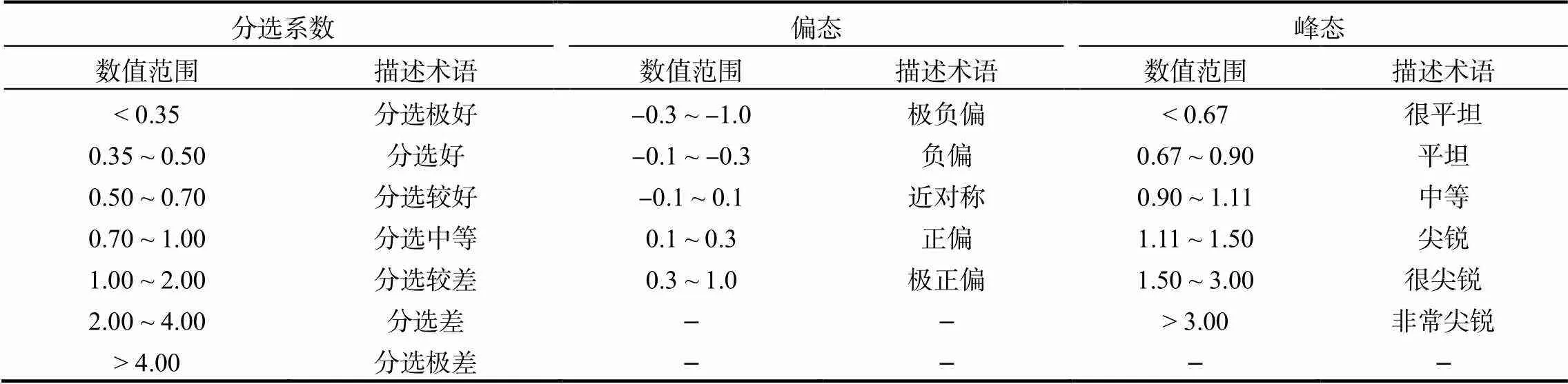
表4 Folk & Ward[1]提出圖解法粒度參數的定性描述術語

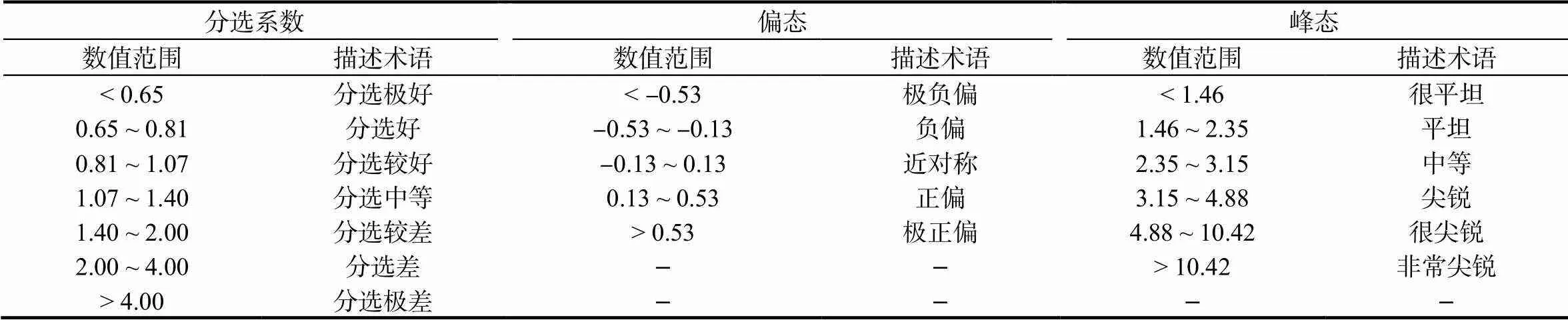
表5 蔡國富等[12]提出的矩值法粒度參數的定性描述術語

表6 賈建軍等[9]提出的矩值法粒度參數的定性描述術語

上述分析表明，并不存在普適于各類沉積環境的矩值法粒度參數定性描述術語標準。因此，在今后粒度參數定性分析過程中，建議使用Folk & Ward圖解法。如選擇了矩值法，則首先要建立其與Folk & Ward圖解法4個粒度參數計算結果的線性轉換關系。如果線性相關關系明顯，則可以仿照賈建軍等[9]和蔡國富等[12]的例子，推算出一個適合于研究區的矩值法定性描述術語參照標準。假若不存在明顯線性關系，則建議使用Folk & Ward圖解法進行粒度參數的計算及其定性分析工作。如在本研究海灘沉積物粒度參數分析中，由于圖解法和矩值法計算得到的偏態或峰態并不存在明顯線性回歸關系，擬合優度僅為0.035 ~ 0.229，故而建議使用Folk & Ward圖解法進行粒度參數計算及其定性分析。

4 結論

本研究利用雷州半島南三島海灘109個表層沉積物粒度數據，對其開展圖解法和矩值法的粒度參數對比研究。在此基礎上，通過數據收集方式統計8種沉積環境的兩類方法計算得到的粒度參數的線性關系，進而系統分析了圖解法和矩值法計算得到的粒度參數之間的關系。本研究得到如下主要認識：

（1）對于南三島海灘沉積物而言，圖解法和矩值法計算得到的平均粒徑和分選系數相關性都比較高（2≥0.821），可以相互轉換，但兩者的偏態和峰態的相關性都比較差（2≤ 0.229），不能相互換算。

（2）對于不同沉積環境的沉積物樣品而言，圖解法和矩值法計算得到的平均粒徑和分選系數的相關性都比較高（2≥ 0.631）。兩類方法計算的偏態和峰態的分選系數在不同沉積環境中有不同體現，在大陸坡、深海盆地和潮灘中擬合優度相對較高（2≥ 0.699），但在河口海岸、海灣和海灘環境，兩者相關性較差。因此，建議在粒度參數定性分析時，首選Folk & Ward圖解法；如選用矩值法，則需建立其與Folk & Ward圖解法的線性轉換關系。

[1] FOLK R L, WARD W C. Brazos River bar [Texas]; a study in the significance of grain size parameters[J]. Journal of Sedimentary Research, 1957, 27(1): 3-26.

[2] GAO S, COLLINS M. Net sediment transport patterns inferred from grain-size trends, based upon definition of “transport vectors”[J]. Sedimentary Geology, 1994, 81(1/2):47-60.

[3] 張才學, 孫省利, 陳春亮. 湛江港灣表層沉積物重金屬的分布特征及潛在生態危害評價[J]. 廣東海洋大學學報, 2006, 26(3): 45-49.

[4] 張才學, 孫省利, 陳春亮. 湛江港附近海域潮間帶海水、沉積物和貝類體內的重金屬[J]. 廣東海洋大學學報, 2011, 31(1): 67-72.

[5] 李自超, 蒲曉強, 趙輝, 等. 湖光巖瑪珥湖表層沉積物粒度特征及其物源指示意義[J]. 廣東海洋大學學報, 2017, 37(3): 93-99.

[6] 黃鑫, 蒲曉強. 熱液活動對海底沉積物中有機質的影響[J]. 廣東海洋大學學報, 2017, 37(1): 117-124.

[7] 馮鈺婷, 彭詩云, 謝輝, 等. 近8000年來珠江口沉積物磁化率及其氣候環境意義[J]. 廣東海洋大學學報, 2018, 38(3): 49-53.

[8] FRIEDMAN G M. Comparison of moment measures for sieving and thin-section data in sedimentary petrological studies[J]. Journal of Sedimentary Research, 1962, 32(1): 15-25.

[9] MCMANUS J. Grain size determination and interpretation[M]//TRUCKER M. Techniques in sedimentology. Oxford: Backwell, 1988: 63-85.

[10] 趙珍清. 南黃海沉積物粒度分布參數計算方法的比較[J]. 海洋地質與第四紀地質, 1992, 12(3): 95-107.

[11] 付莉莉, 馮秀麗, 楊旭輝. 沉積物粒度參數和頻率曲線對粒級劃分的響應[J]. 中國海洋大學學報(自然科學版), 2011, 41(9): 83-89 .

[12] 劉志杰, 龍海燕. 南海沉積物圖解法和矩值法粒度參數計算及對比[J]. 中國海洋大學學報(自然科學版), 2009, 39(2): 313-316, 336.

[13] 徐興永, 易亮, 于洪軍, 等. 圖解法和矩值法估計海岸帶沉積物粒度參數的差異[J]. 海洋學報, 2010, 32(2): 80-86.

[14] 賈建軍, 高抒, 薛允傳. 圖解法與矩法沉積物粒度參數的對比[J]. 海洋與湖沼, 2002, 33(6): 577-582.

[15] 王兆奪, 于東生, 羅福生, 等. 圖解法和矩法計算泉州灣表層沉積物粒度參數的對比[J]. 海洋地質前沿, 2016, 32(7): 19-27.

[16] 劉志杰, 公衍芬, 周松望, 等. 海洋沉積物粒度參數3種計算方法的對比研究[J]. 海洋學報, 2013, 35(3): 179-188.

[17] 蔡國富, 范代讀, 尚帥, 等. 圖解法與矩值法計算的潮汐沉積粒度參數之差異及其原因解析[J]. 海洋地質與第四紀地質, 2014, 34(1): 195-204.

[18] 國家海洋局908專項辦公室. 海洋底質調查技術規程[M]. 北京: 海洋出版社，2006：63.

[19]INMAN D L. Measures for describing the size distribution of sediments[J]. Journal of Sedimentary Research, 1952, 22(3): 125-145.

[20] BLOTT S J, PYE K. GRADISTAT: a grain size distribution and statistics package for the analysis of unconsolidated sediments[J]. Earth Surface Processes and Landforms, 2001, 26(11): 1237-1248.

[21] ZHOU L, GAO S, YANG Y, et al. Typhoon events recorded in coastal lagoon deposits, southeastern Hainan Island[J]. Acta Oceanologica Sinica, 2017, 36(4): 37-45.

Comparative Study on Grain-size Parameters of Marine Sediment Derived from Graphic and Moment Methods

LI Gao-cong1, LI Zhi-qiang1, ZHU Shi-bing1, ZHANG Hui-ling2, ZENG Chun-hua2

（1.//2.,,524088,）

The interconversion relationship between the grain-size parameters of marine sediment calculated by graphic measures (GM) and moment measures (MM) is investigated in this study.First, a comparative study on grain-size parameters of beach sediment of Nansan Island, Leizhou Peninsula, has been carried out. Then, the comparative results of various sedimentary environments are collected to systematically analyzed the transformation relationship between the results of GM and MM.The results show that: in terms of the beach sediment, the mean grain size and sorting coefficient calculated by GM and MM both have a high correlation (2≥ 0.821), which means that they can be converted to each other; but the correlation of the skewness and kurtosis are very poor (2≤ 0.229), which means they cannot be converted to each other; for sediment samples of different sedimentary environments obtained by statistical methods, no general rule of the relationship of particle size parameters between GM and MM is found with the increase of moment; the mean grain size and sorting coefficient of GM and MM can be converted to each other, but there is a great difference in the convertibility of the skewness and kurtosis calculated by GM and MM in different sedimentary environments.It is suggested that the conversion relationship of the grain-size parameters between moment measures and the folk & Ward graphical method need to be clarified, before using MM to describe the physical meaning of the particle size parameters of sediments.

grain-size parameters; graphic measures; moment measures; mutual conversion; sedimentary environments

P736.21

A

1673-9159（2020）06-0096-06

10.3969/j.issn.1673-9159.2020.06.012

李高聰，李志強，朱士兵，等. 圖解法和矩值法海洋沉積物粒度參數的對比[J].廣東海洋大學學報，2020，40（6）：96-101.

2020-04-13

國家自然科學基金項目(41676079); 廣東海洋大學創新強校工程項目(Q18307)

李高聰（1987－），男，博士，講師，研究方向為海洋地質學，Email: ligaocong2013@163.com

李志強（1974－），男，教授，研究方向為海灘過程和海岸工程環境，Email：qiangzl1974@163.com

（責任編輯：劉嶺）