自動駕駛車輛循跡路徑生成算法研究

李晉津 孫二鑫 陳宗娟

摘 要：在無人駕駛領域中 已經實現了車輛按照已有路徑進行循跡無人駕駛 通常已有路徑是由車輛實際采集獲得。文章采用Matlab編寫了循跡路徑的生成算法 解決了循跡路線必須由車輛采集獲取的問題 使車輛控制更加高效。再循跡路徑生成算法中結合了車輛的左右轉最小拐彎半徑約束和允許倒車的情況 得到了無人駕駛車輛可行駛的路徑。最后通過算法生成的路徑進行了實車實驗 車輛能夠按照算法生成的路徑進行自動駕駛 最后對算法生成的路徑和車輛實際路徑進行了對比 驗證了算法的可行性。

關鍵詞：路徑生成;倒車;車輛轉彎半徑;實車實驗

中圖分類號：U495? 文獻標識碼：A? 文章編號：1671-7988（2020）18-16-06

Abstract： In the field of unmanned driving， it has been realized that vehicles follow existing paths to track unmanned driving， Usually the existing path is obtained by actual vehicle collection. this paper uses Matlab to write the algorithm of generating the tracing path， which solves the problem that the tracing route must be acquired by vehicle collection and makes the vehicle control more efficient. The re-tracking path generation algorithm combines the vehicle's left-right tur -ning minimum turning radius constraint and the allowable reversing situation to obtain a path that can be driven by an unmanned vehicle. Finally， a real-vehicle experiment was performed on the path generated by the algorithm. The vehicle can drive automatically according to the path generated by the algorithm. Finally， the path generated by the algorithm is compared with the actual path of the vehicle to verify the feasibility of the algorithm.

Keywords： Path generation; Reversing; Vehicle turning radius; Real car experiment

CLC NO.： U495? Document Code： A? Article ID： 1671-7988（2020）18-16-06

前言

在無人駕駛領域中 軌跡規劃有多種算法 主要分為：1）基于搜索的規劃算法 如：Hybrid A 算法、DLite算法;2） 基于采樣的規劃算法 如概率路線圖（PRM）和快速搜索隨機樹（RRT）算法;3）人工勢場法;4）參數化曲線構造法。本文中循跡路徑算法即采樣的參數化曲線構造方法實現的。

參數化曲線構造法又分為多項式曲線 貝塞爾曲線樣條曲線和Dubins（直線和圓弧）。Andrei M Shke等人對dubins曲線進行了研究 對起始點的姿態進行了坐標變換 完成了各類情況的路線計算[1];劉流等研究了帶速度約束的dubins路徑 研究表明 拐彎半徑是速度的函數 當速度較大時 需要匹配更大的轉彎半徑 并進行了無人機飛行驗證[2];吳克風等人針對起終點距離較近情況 進行了不同情況下的分類 推導了并驗證了各類情況下的最短路徑情況[3];楊秀霞等人 考慮了角度約束 即起始轉彎半徑不同情況下的路徑 并對不同角度下的路徑進行了分析對比[4]。黃得剛等人，研究了三維Dubins路徑 即在位置中加入不同的高度z 其核心主要是對起終點不同高度進行插值 并對三維Dubins路徑進行了仿真實驗[5]。

目前基于倒車和起始點轉彎半徑（曲率）不同的Dubins路徑研究較少 而加入倒車模式會得到更短的路徑并在某些特定的領域如避障 自動泊車等方面大有所為。本文研究了加入倒車和選擇不同的起始轉彎半徑情況下的Dubins路徑 算法另辟蹊徑 解決了車輛循跡路徑生成問題。

1 問題描述

在一個二維平面中 尋找兩個帶方向的點間的最短光滑路徑。起點為A（xa，ya） A點頭車朝向為αa 車頭朝向與地理方位角一致 即正北為0度 范圍為[0-360];終點為B（xb，yb） 終點車頭朝向為αb。尋找從起點A到終點B的最短光滑路徑。車輛的轉彎半徑設置為R 受車輛最小轉彎半徑約束 R選取應大于車的最小轉彎半徑。

2 約束條件

2.1 車輛的轉彎半徑約束

2.1.1 轉彎半徑

由于車輛的結構特征存在最小拐彎半徑 有些車輛的左轉最小拐彎半徑和右轉最小轉彎半徑還可能不相同 如圖2所示 已知A點的位置及方位角αa 由一個特定的位置出發 車輛在下一步只能到達它可能到達的位置 受制于汽車最大轉彎半徑的限制。下圖中紅色箭頭表示車輛在最大拐彎半徑情況下的極限可行駛方向 藍色表示直行。車輛前方區域表示正向行駛的區域 范圍為極限右轉與極限左轉之間;車輛后方為倒車情況下的可行駛區域;范圍也為為極限右轉與極限左轉之間。那么只要給定車輛的拐彎半徑大于車輛的極限拐彎半徑 車輛是可以行駛的。

2.1.2 實車轉彎半徑參數

本次實驗采用的是傳祺GE3改裝的自動駕駛車輛 最大拐彎半徑根據實車采集數據獲取如圖3所示 車輛的左轉和右轉情況具有不同的最大轉彎半徑 左轉最大轉彎半徑為3.75m 右轉最大轉彎半徑為4.2m。

2.2 倒車約束約束

如下圖所示 在某些情況下 正向行駛會走更長的路程 例如終點在起點的正后方 且車頭朝向和初始車頭朝向一致 這樣車輛只需掛倒擋即可實現到達終點。又如當車輛從A點出發 通過固定的拐彎半徑可以實現到達終點B且滿足到達B的車頭朝向 同時車輛也可以掛倒擋實現到達終點B且滿足B點車頭朝向。對比發現 掛倒擋走的路徑要遠小于前進走的道路。因此對于任意車輛可走的圓弧 均有兩種到達方式 一種時正向行駛 一種是后退行駛 走的弧段大于半圓稱之為劣弧 走的弧段小于半圓稱之為優弧。因此車輛在加入倒車模式后 在某些情況下能夠得到更短的路徑。

文中以f（forward）表示向前行駛 以b（back）表示倒車行駛 故對應于直線情況 將AB直線記為 前進直線路徑記為 倒車直線路徑記為。對于圓弧路徑情況 將起終點圓弧記為 那么向前行駛弧AB記為 倒車行駛AB記為。

3 算法實現

3.1 算法構思

對于任意位置任意車頭朝向的兩個起終車位點 無論情況怎樣復雜都可以將其劃分為如圖四種情況 即考慮實際情況 車輛可以左轉出發也可以右轉出發 到達終點可以是左轉到達或者右轉到達。

假設在不考慮避障及車輛速度情況下 認為在任意位置車輛都可以按車頭反方向倒車行駛。

實際路線為車輛從起點A以拐彎半徑R走圓弧（向左或向右） 接著直行走起終點兩個圓弧的公切線 最后以拐彎半徑R走圓弧到達終點B 即路線為圓弧-直線-圓弧路線。可將所有情況都列出 最后對到達終點過程中是否有倒車情形及到達終點車頭的正反向情況進行分類。將行駛過程中有無倒車狀態記為'Back'或者'Noback';將到達終點B與目標車頭朝向的正反狀態記為'Positive' 'Reverse';那么所有狀態可以為：'PositiveNoback' 'PositiveBack' 'ReverseNoback' 'Reverse Back'四種。四種狀態分別表示為：到達終點正向且行駛中無倒車情形;到達終點正向且行駛中有倒車情形;到達終點反向且行駛中無倒車情形;到達終點反向且行駛中有倒車情形。編寫算法計算求出所有存在的路徑 并對路徑的狀態進行標注。

編寫選擇路徑算法 一般情況下 更為關心的是行駛過程中無倒車情形且到達終點B頭車朝向一致的路徑。選擇最短的作為最終需求的路徑。最后按需提取不同狀態路徑即實現了路徑的生成。

3.2 路線說明

3.2.1 基礎路徑

以圖5左上圖（從起點A右邊出發 左邊到達終點B情形）為例進行說明 從A到B有4種路線 分別是黃色 綠色 藍色 紫色四種路徑。1.黃色路徑為（圓弧 直線 圓弧）;2.綠色路徑為（圓弧 直線 圓弧）;3.藍色路徑為（圓弧 直線 圓弧）;4.紫色路徑為（圓弧 直線 圓弧）。

3.2.2 實際車輛行駛路徑

根據圓弧的可正向行駛和反向行駛的特征 到達一個圓弧處的終點B有兩種方式到達 根據上述路線需要走兩個圓弧 故每一條路線 可以有四種行駛方法。具體以圖6為例黃色路線為例進行說明車輛可能行駛路徑為①（）②（）③（ ）④（ ）。

3.2.3 路徑狀態標注

對圖6路徑進行分析可以發現該路線到達終點B的車頭朝向與需求的正好相反 其中只有路徑①沒有倒車行駛情況。那么路徑①的狀態為'ReverseNoback' 其他的路徑狀態為'ReverseBack'。圖5中第一種情況路徑狀態見表1 其它三類情況類似 均可求出每條路徑的狀態 故其他三類情況不在贅述。

3.3 算法實現步驟

3.3.1 求圓心

以A點為例 輸入為（xa，ya，αa）及拐彎半徑R 可以求得左右共兩個圓的圓心位置。輸出為圓心CA（xi，yi）（i=1，2） 同樣終點B處可以求取兩個圓心CB（xj，yj）（j=1，2）。

式中 x y為圓心的橫縱坐標;xa ya為起點的橫縱坐標位置;αa為起點車頭朝向;中+表示右側圓心位置的求法 -表示左側圓心位置的求法。

3.3.2 求兩圓公切點

根據兩圓相切公切線存在情況 如圖7 當兩個圓的半徑相同時存在四種情況即：有四組公切線（兩圓相離） 三組公切線（兩圓外切） 兩組公切線（兩圓相交） 沒有公切線（同心圓 即兩圓重合）。

求取兩個圓相切的所有切點對。輸入參數為CA（xCA? yCA） RA CB（xCB yCB） RB;輸出參數為公切點對 即兩個切點組成的切點對 如圖8所示外公切線中的切點對[A1，B1] [A4，B4]及內公切線中的切點對[A2，B2] [A4，B4]。計算公式如下：

3.3.3 路徑生成

只需將圓弧或者直線路徑求出 按照圓弧-直線-圓弧路線生成軌跡路徑即可 三段路徑可用相同的算法進行編寫。輸入參數為：起點位置及車頭朝向A（xa，ya，αa） 終點位置A1（xa1，ya1） 向前或者向后行駛（forwardorback） 輸出為終點車頭朝向αa1 路徑長度dAA1 離散路徑序列點 （xi，yi，αi）。由于路徑為離散采樣 可以根據不同的需求進行設計 如等長度分割 等數量分割等。算法實現詳細如下圖所示。

4 算法仿真結果

4.1 路徑展示

4.1.1 路徑情形展示

對于任意位置 任意車頭朝向的兩個起終點 根據圖5所示 一種情況最多有16組路徑 4種情況共計最多有64種解。例如A點（0，0，0） B（15，15，315） 拐彎半徑R=5。如圖所示為存在64組解的所有情況。具體路徑圖見圖10-13。

4.1.2 路徑分類統計

根據展示的所有路徑 對路徑分類統計結果如下表所示。

4.2 路徑篩選結果對比

選擇符合要求的路徑進行分析顯示 一般情況下 更關注正向的沒有倒擋情況下的路徑即'PositiveNoback' 此外在有倒車情形下的最短路徑'Positive'也是非常關注的 下面通過不同的參數對比兩者路徑中的最短路徑。

4.2.1 轉彎半徑相同時 各類情況路徑對比

（1）對比AB直線距離不同情況下的路徑;設置起點A位置為（0，0，0） 車的拐彎半徑R=8 設置起終點車頭朝向αb=60° B點與A點距離分別為0 R 2R 3R情況下的路徑對比如下。

（2）B點與A點距離固定B點的車頭朝向不同情況下的路徑;設置起點A位置為（0，0，0） 車的拐彎半徑R=8 設置起終點B在A的某個象限 B點車頭朝向不同情況下的路徑對比如下。

（3）B點與A點距離固定 B點車頭朝向固定 B位于A不同象限情況下的路徑。設置起點A位置為（0，0，0） 車的拐彎半徑R=8 設置起終點車頭朝向αb=60° B點分別位于A的不同象限情況下的路徑對比如下。

綜合對比可以得出：算法可以找到任意復雜情況的最短路徑;加入倒車情形會得到更短的路徑。

4.2.2 轉彎半徑不同時 不同類別路徑對比

設置起點A位置為（0，0，0） 車的起始拐彎半徑RA=8 設置起終點B位置為（0，0，0） 到達B點拐彎半徑分別設置為RB=[5，8，11，14] 三種不同類型（'PositiveNoback';'Positive';' ReverseNoback'）情況下的路徑對比如下。

4.2.3 結論

對比曲線可以得出以下結論。1、不同轉彎半徑約束下 半徑越大會得到更長的路徑里程;2、加入倒擋模式在某種情況下會得到更短的路徑 倒車路徑的影響范圍比沒有倒車情況更小 倒車路徑的控制復雜度要高于沒有倒車情形的路徑;3、所有路徑中存在到達B點但與預期的車頭朝向相反的路徑 且在某些情況下會有更短的路徑 當某些場合不太關注車頭的正反向時有重要意義。

5 實車驗證

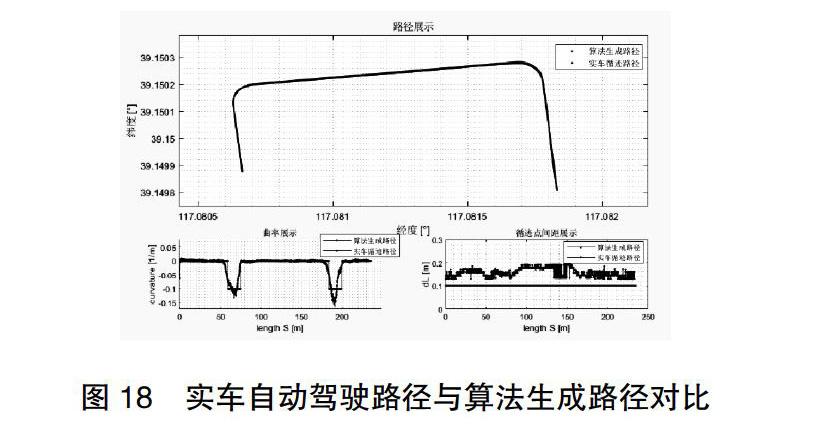
通過仿真結果可以給出任意情況下 起終點的連接路徑 算法在自動駕駛場地進行了實車測試 對比結果如下圖：

根據路徑展示情況可以看出 實車循跡路線與算法生成的路線基本吻合 僅在拐彎處存在一定的誤差;分析曲率變化情況可以看出 算法生成的曲率平滑 當曲率為0表示直行 曲率為-0.1表示車輛以拐彎半徑為10m進行左轉 實車循跡路線的曲率為緩慢增大再變為0 這是由于車輛控制算法導致的 車輛完成左轉首先需要逐步左打方向盤 待完成拐彎后方向盤回正 表現出來的是曲率的絕對值先增大后減小;點距為采樣點 算法生成的路線點是10cm一個點 實車采樣點距為10cm～20cm之間。

通過實車實驗 驗證了算法的可行性 大大提高了無人駕駛車輛的測試效率 解決了要進行測試首先需要車輛去錄制軌跡數據這一“痛點” 在實踐中得到廣泛應用。

最后算法在車輛遠程控制中得到應用 將算法集成在web端 通過遠程路徑下發來控制無人駕駛車輛自動駕駛至目的地。

6 結束語

本文通過詳細介紹了自動駕駛循跡路線生成算法 通過該算法生成的路徑可指導自動駕駛車輛按照路徑進行自動駕駛。解決了自動駕駛車輛必須先錄制車輛軌跡路徑才能進行自動駕駛的弊端。極大的提升了控制的靈活性。

通過實車進行了測試 在空曠的無人駕駛場地中自動駕駛車輛按照算法生成的既定路線進行自動駕駛。

參考文獻

[1] Andrei M Shkel，Vladimir Lumelsky. Classification of Dubins set[J]. Robotics and Autonomous Systems 2001，34，179-202.

[2] 劉 流，梁曉龍，何呂龍，等.考慮速度約束的無人機Dubins路徑規劃[J].火力與指揮控制，2018，43（12）：50-58.

[3] 吳克風，曹曉文，周其忠，等.任意距離下Dubins最短路徑研究[J].戰術導彈技術，2017，1：76-84.

[4] 楊秀霞，曹唯一，張毅.時間和角度約束下的雙圓弧路徑規劃[J].空間控制技術與應用，2019，41（8）：1835-1843.

[5] 黃得剛，章衛國，楊立本.無動力無人機進場階段三維Dubins路徑跟蹤方法[J].系統工程與電子技術，2016，38（3）：629-637.