某履帶裝甲車輛傳動齒輪系疲勞載荷研究

魏領軍，劉海鷗，陳慧巖，石 鋒

（1.北京理工大學，北京 100081；2.北京交通運輸職業學院，北京 102611；3.中國汽車工程研究院，重慶 401122）

在現代軍事戰爭中，履帶裝甲車輛良好的越野性能使其在陸軍地面武器中具有不可替代的作用[1]。隨著現代新技術的發展，履帶裝甲車輛通常把傳動、操縱、轉向、制動、液壓控制系統集成一體，即綜合傳動系統[2]。傳動齒輪系作為綜合傳動系統的核心部件，其編譜技術的研究與產品設計息息相關，并涉及多種學科和領域，準確的載荷譜在強度研究及產品設計中是必不可少的，所以傳動齒輪系載荷譜研究具有十分重要的實用價值[3]。鑒于傳動齒輪系載荷譜在指導試驗和設計方面的重要作用，國內外眾多行業都把其列為高密級的重點研究課題，研究成果極少對外公開[4]。

我國對履帶裝甲車輛傳動齒輪系轉矩測試數據有一定的積累，但未形成完整、規范的轉矩載荷譜，傳動齒輪系設計基本上是根據經驗估計轉矩載荷條件，與實際轉矩載荷情況有一定差距，導致了傳動齒輪系過設計或使用過程中出現傳動齒輪斷裂等問題，制約了我國履帶裝甲車輛綜合傳動技術的發展[5]。為了進一步提升我國履帶裝甲車輛傳動系統的設計和試驗驗證能力，逐步實現由基于靜載荷的安全系數法向基于載荷譜的疲勞設計法轉變，對于實車傳動齒輪系載荷編譜技術的研究是十分必要的[6]。

1 峰值計數技術

LMS TecWare的峰值計數原理如圖1所示，其實質是統計隨機時域數據的載荷極大值和極小值的分布。

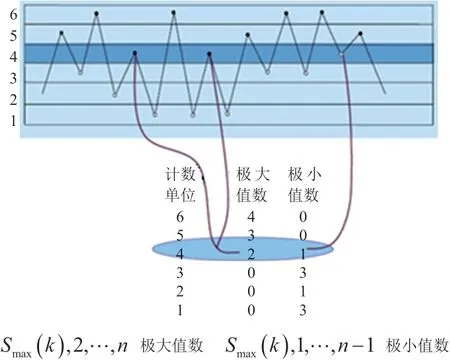
圖1 峰值計數技術原理

把試驗修正過的13個左輸出軸轉矩時域的數據樣本在LMS TecWare中進行峰值計數，典型結果（021號樣本）如圖2所示。

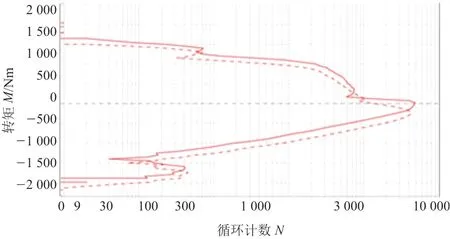
圖2 021號樣本數據峰值計數結果

由圖2可知，極大值點（虛線）的分布比極小值點（實線）的分布在絕對數值上明顯偏大，因此，只需按照極大值點的統計分布來指定和獲得具有一定置信度的最大值即可。

2 參數估計

將試驗獲得的全部6名駕駛員的樣本數據峰值計數結果匯總，得到一個極大值點分布的大樣本數據，其中左、右輸出軸的數據結果分別如圖3和圖4中的藍色柱狀圖所示。

假設左、右輸出軸轉矩極大值服從正態分布，則通過極大似然法獲得左輸出軸轉矩極大值的平均值為1 313 Nm、標準差為1 662 Nm，可得圖3中黑色的正態分布擬合線；右輸出軸轉矩極大值的平均值為1 369 Nm、標準差為1 688 Nm，可得出圖4中黑色的正態分布擬合線。

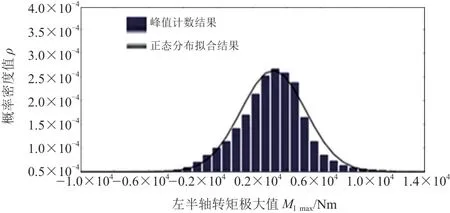
圖3 全部數據樣本獲得的左輸出軸極大值分布結果的正態分布擬合結果

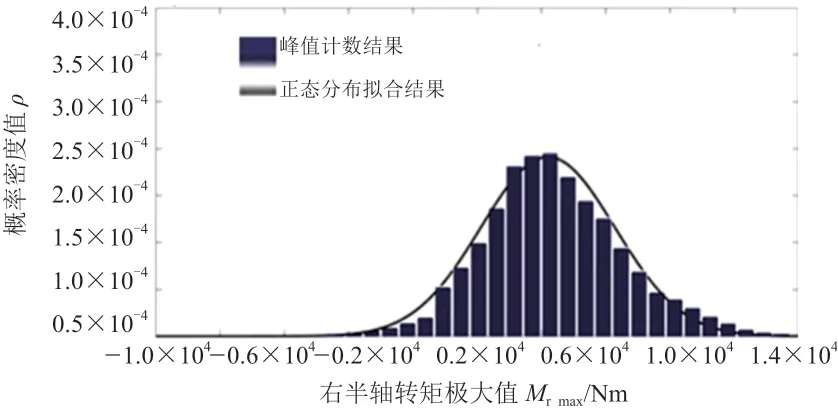
圖4 全部數據樣本獲得的右輸出軸極大值分布結果的正態分布擬合結果

對照圖3和圖4，全部數據樣本獲得的左、右輸出軸極大值分布結果的正態分布擬合狀況有稍許的差異，造成這種差異的主要原因是試驗用車的左、右傳動軸結構非完全對稱，以及數據采集過程中出現上、下坡轉向。

3 由極大值分布獲得最大值分布

經統計全部樣本數據獲得了極大值的正態分布，然后由極大值分布獲得最大值分布，并在此基礎上最終給出設計譜。

設X1,X2, …,Xn獨立同分布于分布函數f(x)和密度函數f(x)，記Y= max (X1,X2, …Xn)，則Y有概率密度函數nFn-1(x)f(x)[7]。對于一維隨機變量，最大值Y有概率密度函數F0(x)f(x)=f(x)，對于一維隨機變量來說，最大值與極大值同分布，即左轉矩最大值服從N[1 313 Nm，（1 662 Nm）2]的正態分布；右轉矩最大值服從N[1 369 Nm，（1 688 Nm）2]的正態分布。

既然左轉矩最大值服從N[1 313 Nm，（1 688Nm）2]的正態分布，那么可以根據正態分布表，給出具有一定置信度的極大值置信區間上界作為設計譜。比如說，如果指定置信度為99.999%，則設計譜為2 996 Nm，其統計學意義是：在實際使用環境中，左輸出軸承受的最大轉矩值大于2 996 Nm的概率僅為（1-99.999%），即百萬分之一。對于右轉矩來說，對應的數值為3 158 Nm。

4 車輛起伏路面行駛時的雨流譜和階次譜

針對傳動軸制定臺架試驗方案，需采用雨流循環測試方法，以試驗對象件（傳動軸）所經受的真實損傷（而不是偽損傷）為依據，將真實損傷“搬”到臺架上。該技術首先對傳動軸所承受的隨機轉矩時域數據進行雨流計數，得到載荷譜后，再以損傷等價為基礎編輯得出階次譜。

4.1 雨流譜

針對試驗處理后的數據分別生成與它們對應的雨流譜，從6名駕駛員中選出具有代表性的駕駛員A，其全部數據生成的左、右傳動軸雨流譜如圖5所示；通過駕駛員A全部數據生成的左、右傳動軸雨流譜圖形對照可知，所采集數據的可信度較高。

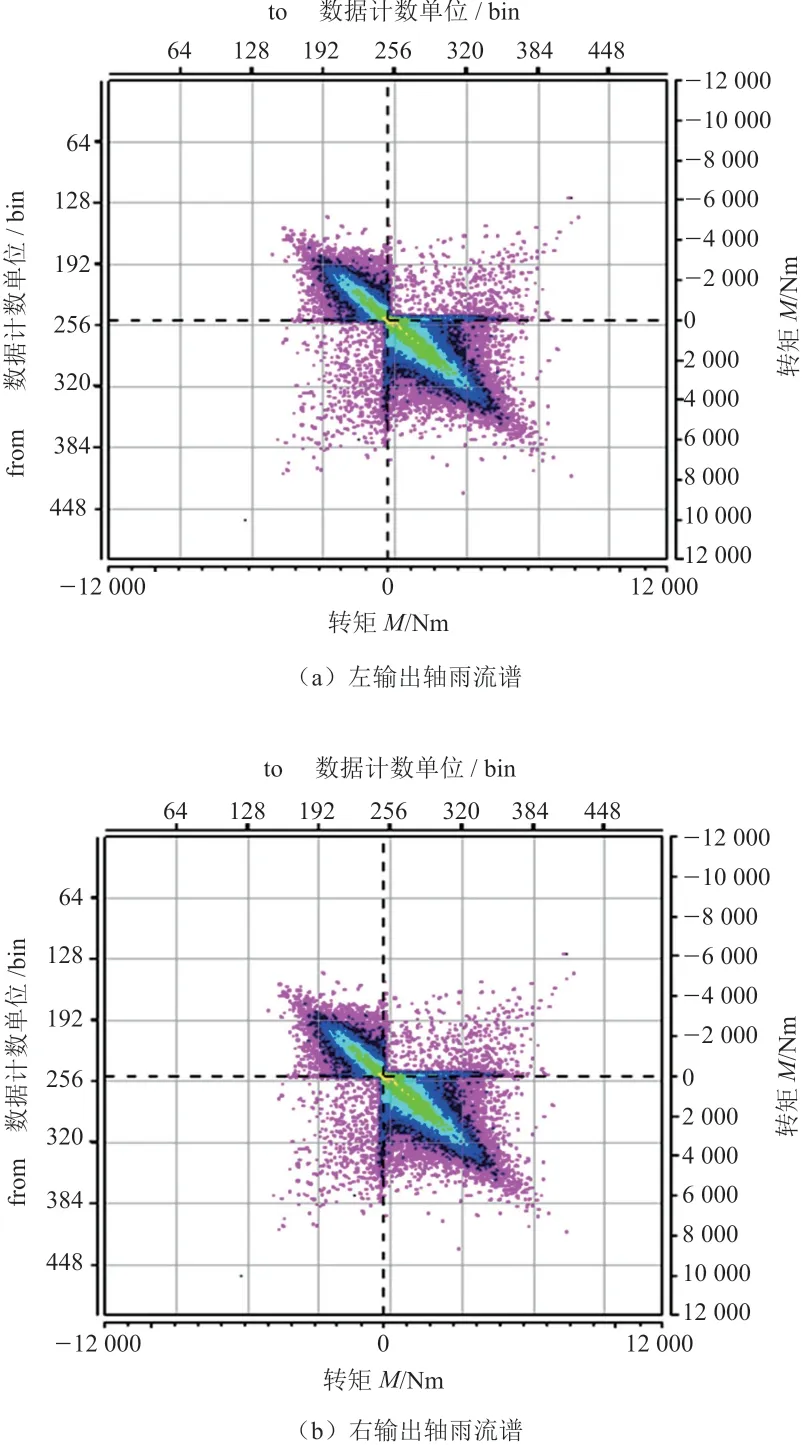
圖5 駕駛員A的雨流譜

4.2 階次譜

在階次譜編輯過程中，需要結合傳動軸材料的真實S-N曲線（本研究中b=5，疲勞極限為1 000 MPa，對應107循環），在考慮平均剪應力的影響（圖6）情況下，采用Lsegment平均剪應力修正模型，取系數為0.300，計算真實損傷；將雨流計數矩陣中的每個載荷進行等效損傷平均應力轉換，使其成為對稱載荷循環，即將均幅值二維載荷譜轉換成以幅值為變量的一維載荷譜，然后再次運用等損傷方法將一維載荷譜的幅值轉換成8級譜，并針對這8個等級載荷所造成的真實損傷，計算在試驗臺架上不同載荷幅值等級和頻次的載荷旋轉次數，從而完成試驗方案的初步制定。其主要思路如圖7所示。

圖6 局部平均剪應力修正模型圖

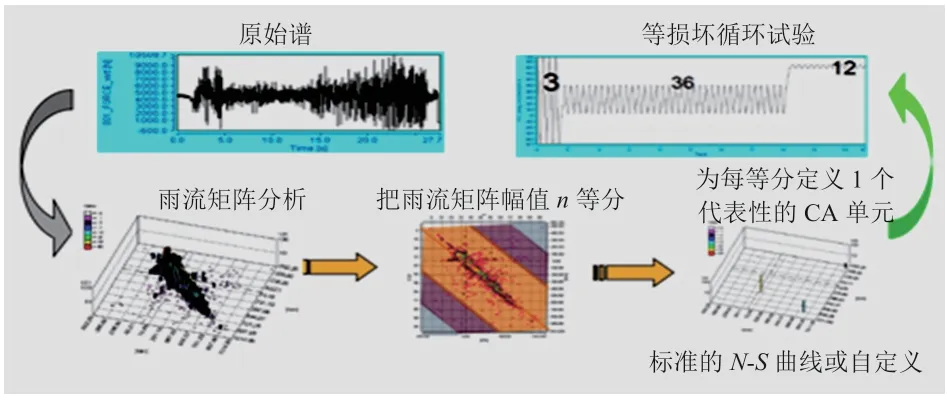
圖7 雨流循環測試方法

用不等間隔及等效方法將一維載荷譜轉換為8級程序譜，即采用等損傷方法，將幅值在1級與2級之間的載荷循環，分別轉換成對稱幅值為1級和2級的載荷循環，將幅值在2級與3級之間的載荷循環，分別轉換成對稱幅值為2級和3級的載荷循環，然后依此類推，將全部數據的對稱載荷循環轉換為8個幅值級別的對稱載荷循環[8]。等效損傷轉換公式為：

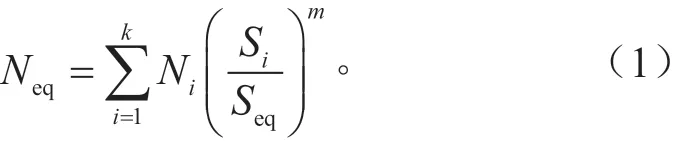
式中：Seq和Neq分別為等效載荷循環的幅值和頻次；Si和Ni分別為原載荷循環的幅值和頻次；m為S-N曲線的冪指數。把小幅值高頻次載荷循環轉換成大幅值低頻次的載荷循環，對載荷譜疲勞試驗起到加速作用。基于雨流循環測試方法制定的左輸出軸8級階次譜見表1。

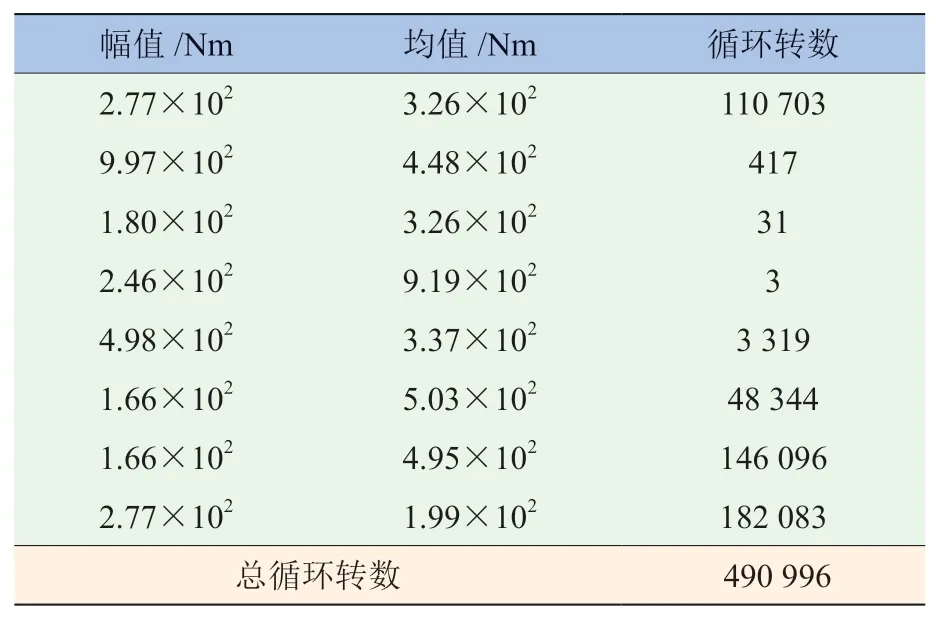
表1 基于雨流循環測試方法制定的左輸出軸8級階次譜

5 損傷數

假設用于制造相關齒輪材料的S-N曲線（循環載荷比R=0）為N·Sb=C（式中，N為循環轉，S為載荷幅值，b為材料參數），則齒輪在隨機載荷作用下疲勞危險部位所受到的損傷D為[9]：

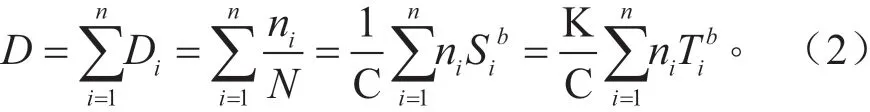
式中：假定齒根疲勞危險點應力水平S與軸轉矩T之間呈線性關系，S=KT（K為常數）；ni為對應于軸轉矩數值為Ti的旋轉頻數（也就是齒所遭受的交變轉矩在水平為Ti的次數）。

由式（1）可知，由于C與K都為常數，所以對齒根疲勞危險部位造成真正損傷的載荷量值為該數值被稱為“損傷數”。在制定臺架試驗方案時，需將具有統計代表性和滿足設計目標的損傷數“搬”到臺架上，以完成相關的考核驗證。要實現這一目標只需確定材料參數b即可完成。

6 旋轉直方圖技術

為了計算損傷數（圖8），需要6個前進擋和1個倒擋的轉速與轉矩信息。同時，需要把轉矩分割為足夠小的bin區間，通過把落入相應bin區間內的轉速進行時間積分，在恒定水平的轉矩Ti作用下，可得與轉矩水平相應的齒輪旋轉速度ni，從而得到足夠多的用于計算損傷精確的（ni，Ti）數據對[10]。上述過程集成在“旋轉直方圖”中，其相關技術是制定穩態旋轉臺架試驗方案的關鍵。

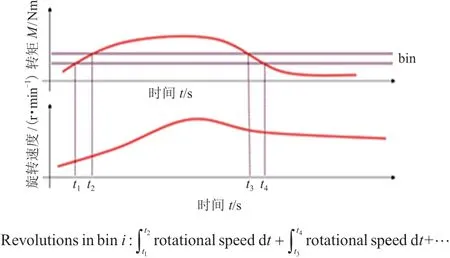
圖8 旋轉直方圖技術原理

分別把全部樣本數據分解到6個前進擋和倒擋R的載荷（主要指轉矩和轉速）進行旋轉直方圖統計，并作為制定臺架試驗載荷譜的關鍵基礎數據。在此過程中將產生大量的重要過程數據和圖標，是制定面向傳動齒輪系統試驗譜的核心基礎數據。

7 試驗載荷譜的制定

試驗載荷譜制定的總體思路如圖9所示。采集到的數據來自于6名駕駛員的不同樣本。首先把每個駕駛員的數據樣本放大到相應的總設計里程。在涵蓋98%駕駛員的駕駛習慣下，分解到6個前進擋和倒擋R的相應擋位的設計里程為10 000 km。在起伏路面以5擋行駛時從6名駕駛員的數據中選出3個有代表性的數據，將相應的旋轉直方圖計數結果進行相應比例的放大，其結果見表2。

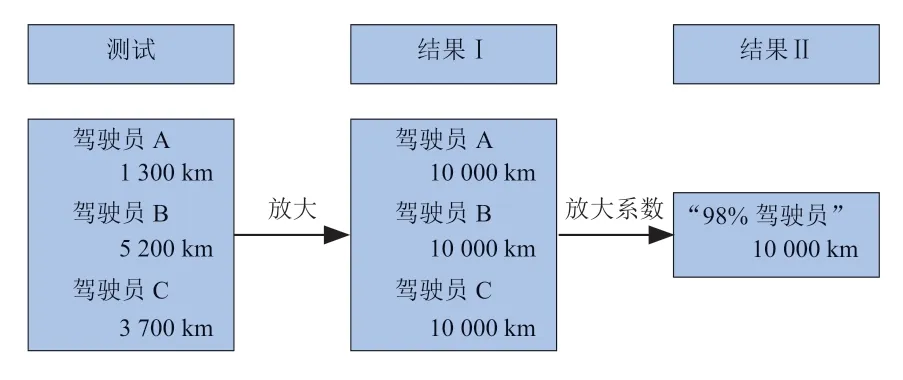
圖9 臺架試驗方案的制定思路

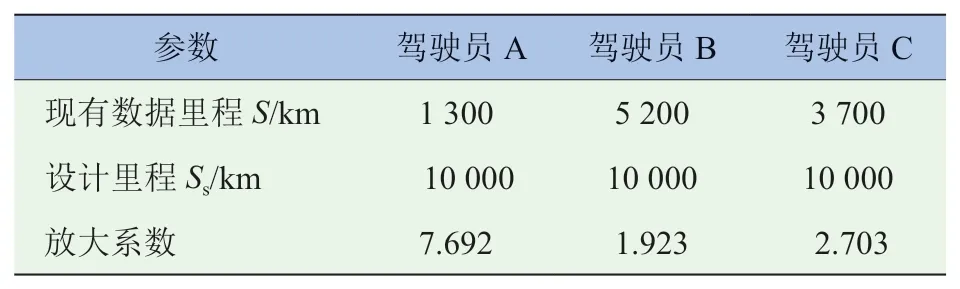
表2 三名駕駛員5擋行駛的放大結果

在此基礎上，需要考慮到駕駛員的駕駛習慣，給出帶有分位數的外推結果。然而，由于樣本數比較小，只有6名有效駕駛員（N=6），所以采用一種特殊的統計方法，以98%的精度來計算駕駛員的特性。先對6名駕駛員在各自區間內的總轉數進行平均，其值為再確保轉數分布置信水平在98%以上。參照1973年Lipson的研究[11]，利用式（3）計算置信水平為98%的用戶轉數分布x98%。

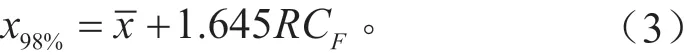
式中：R為轉矩區間最大轉數與最小轉數之間的差值；它的標準差系數參照表3所示，在本試驗過程中Cf的標準差系數為0.812；1.645為置信水平為98%時標準正態分布中的值，若需提高置信水平或其它置信度，可參照相應的統計公式進行更改，本文中這一數值全部取為98%。

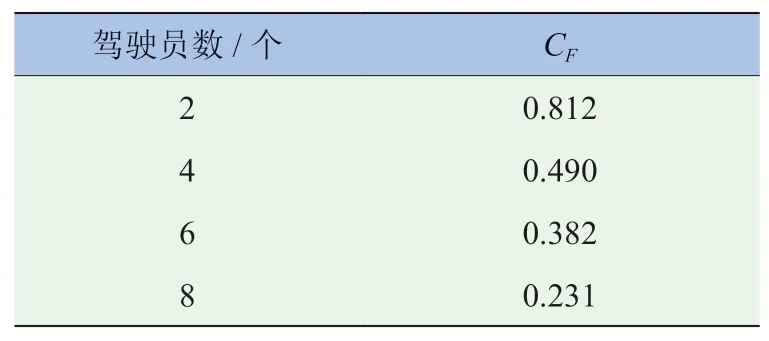
表3 一個區間的標準差系數

下文以履帶裝甲車輛常用的5擋位行駛為例，進行行駛試驗譜的制定，分析其試驗譜制定過程，其分析過程對于其它擋位也相同。

涵蓋98%駕駛員駕駛習慣的、分解到以5擋位行駛的設計里程為6 738 km，將相應的旋轉直方圖計數結果進行相應比例的放大，其結果見表4。

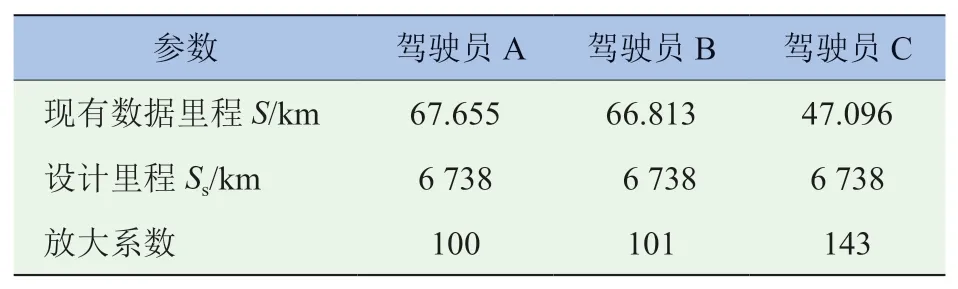
表4 以5擋位行駛的放大倍數結果

考慮到駕駛員的駕駛習慣，獲得置信水平為98%，總設計里程為10 000 km且保持5擋行駛的T-n結果（轉矩-循環數）。在此基礎上，采用相等的損傷數來制定臺架試驗計劃即可。在5擋位行駛工況下，齒輪材料的S-N曲線b=5，則如上所述，損傷數為[12]：

為了給試驗譜選擇合適的轉矩，如圖10所示，通過旋轉直方圖計數給出了部分代表性樣本數據的總累積損傷分布圖。由圖可知，以5擋位行駛時載荷比較平穩，因此，在1 400 Nm轉矩水平上進行臺架試驗（表5），在此基礎上，在損傷數等效的約束下，確定轉矩為1 400 Nm時需要旋轉5 164 904轉。

表5 以5擋位行駛時設計總里程的試驗結果

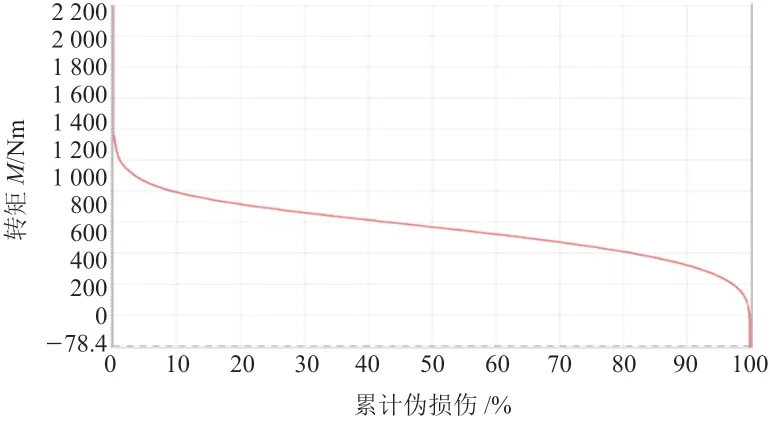
圖10 部分樣本數據的總累積損傷直方圖

當部分代表性樣本以5擋位行駛時，對相應的發動機轉速數據進行幅值概率密度分布分析，如圖11所示，得到發動機轉速的幅值概率密度分布結果。由圖可知，以5擋位行駛時發動機轉速最有可能出現在1 800 r/min，以此確定在轉矩為1 400 Nm時，應以1 800 r/min的發動機轉速將試驗持續47 h 50 min。

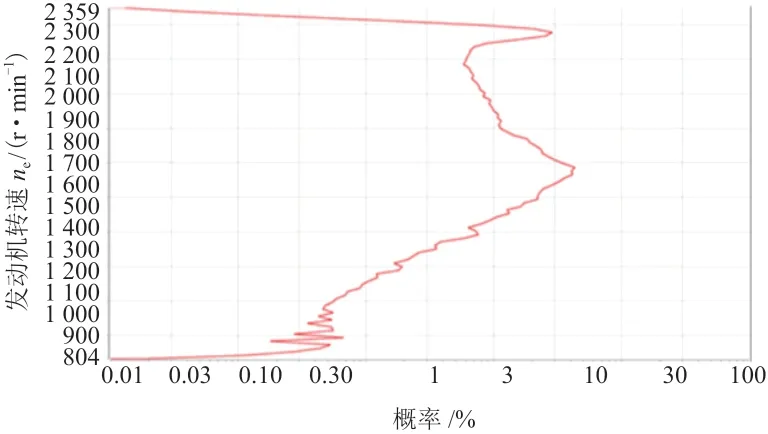
圖11 以5擋位行駛時發動機轉速幅值概率密度分布

8 穩態旋轉臺架試驗方案

經過上述數據處理，最終可得針對傳動軸的穩態旋轉臺架試驗方案，見表6。該方案對應履帶裝甲車輛在起伏路面上行駛10 000 km時的設計里程。

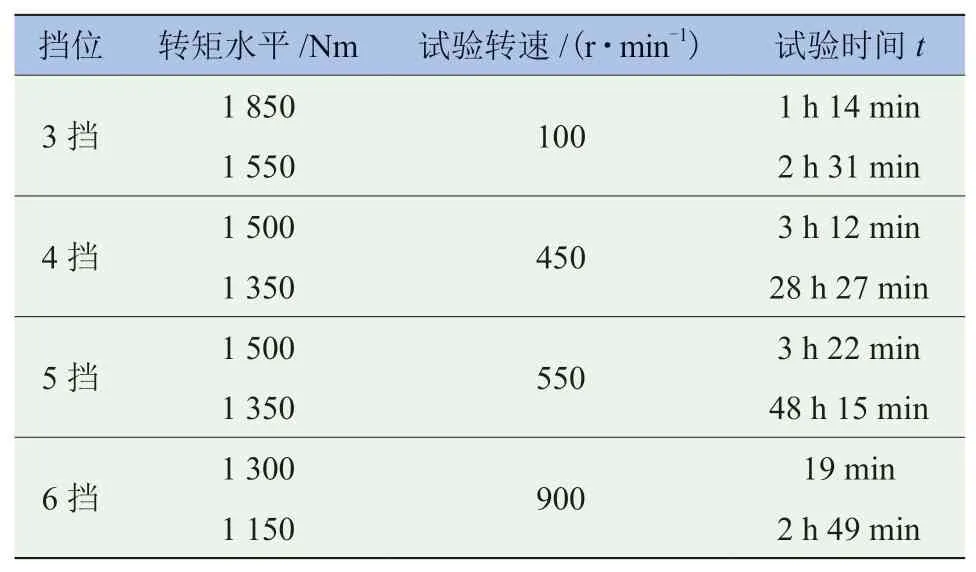
表6 綜合傳動軸穩態旋轉臺架試驗方案

9 生成具有指定置信度的設計譜

經證明可知，左輸出軸轉矩極大值服從N[1 161.562 Nm，（4 620.004 Nm）2]的正態分布，那么，根據正態分布表可以得出具有一定置信度的極大值置信區間上界值，作為設計譜安全設計限值，圖12所示為13個數據樣本獲得的左輸出軸極大值分布結果及正態分布擬合結果，由圖可知設計譜的可靠性較高。

利用統計學正態分布及F檢驗原理，在實際使用環境中，左輸出軸承受的轉矩極大值大于2 294 Nm的概率僅為（1-99.999%），即百萬分之一。如果指定置信度為99.999%，則設計譜為2 294 N，從而證明了設計譜的可靠性。

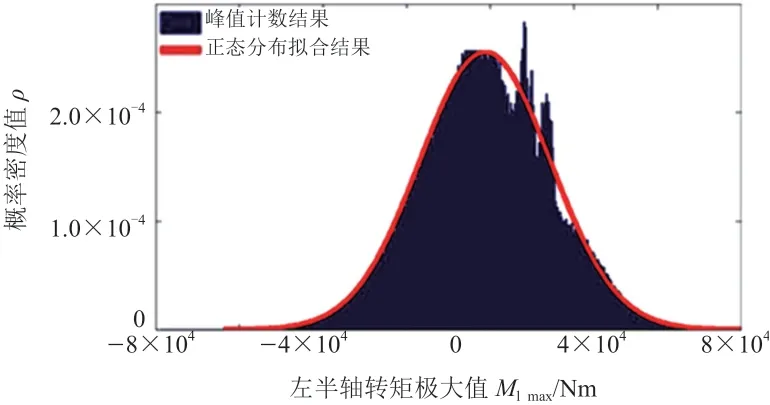
圖12 13個數據樣本獲得的左輸出軸極大值分布結果及正態分布擬合結果

10 結論

本研究針對起伏路面行駛時采集后去毛刺和偏置糾正數據樣本（主要為傳動軸轉矩和車速時域數據），制定了傳動軸的轉矩試驗載荷譜，采用雨流循環測試方法，結合傳動軸材料的真實S-N曲線，分析了車輛在起伏路面行駛時的載荷譜和階次譜，以及綜合傳動系統的試驗譜。根據不同幅度的載荷所造成的損傷形成了8級譜，并針對這8個等級的載荷所造成的真實損傷，計算在試驗臺架上所需要重復的轉數，將轉速、轉矩和車速信息按照履帶裝甲車輛行駛擋位進行分割，對于每個行駛擋位制定穩態旋轉臺架試驗方案。在分析過程中，將車輛的總設計歷程和軸轉矩載荷的不確定性納入考量，并將擋位分割及統計各擋位數據里程，以此形成試驗載荷譜的制定方法，最后形成穩態旋轉臺架試驗方案。

按照峰值計數方法的極大值點的統計分布來獲得具有一定置信度的最大值，參照極大值分布函數推導出最大值分布，并在此基礎上最終給出設計譜。該編譜技術為履帶裝甲車輛傳動軸疲勞設計提供部分參考，并推廣應用于工程或民用車輛傳動件的抗疲勞設計中，具有一定的實用價值。