帶預(yù)設(shè)性能的火箭垂直著陸段姿態(tài)自適應(yīng)控制設(shè)計(jì)

李璟瀾,楊秦敏

(浙江大學(xué)控制科學(xué)與工程學(xué)院, 杭州 310027)

0 引言

研制低成本、高可靠、高效率的運(yùn)載器一直是航天界追求的目標(biāo)[1]。實(shí)現(xiàn)運(yùn)載火箭各子級(jí)的無損回收，從而通過重復(fù)使用來分?jǐn)傔\(yùn)載火箭的發(fā)射成本，是可行的技術(shù)途徑之一[2]。目前，SpaceX公司Falcon 9系列火箭的多次成功回收，也再次證明了垂直起降重復(fù)使用模式的可行性[3-4]。

垂直著陸段的姿態(tài)控制是可重復(fù)使用火箭的關(guān)鍵技術(shù)。考慮火箭子級(jí)返回過程中，其姿態(tài)角和角速度呈現(xiàn)復(fù)雜的非線性耦合特性，且存在氣動(dòng)參數(shù)偏差、嚴(yán)重環(huán)境干擾以及火箭自身燃料變化引起的重心和轉(zhuǎn)動(dòng)慣量變化等，經(jīng)典控制方法往往難以保證控制系統(tǒng)的精度和穩(wěn)定性。因此，需要設(shè)計(jì)更為先進(jìn)的控制系統(tǒng)以滿足火箭垂直返回段姿態(tài)跟蹤的性能需求。

周軍等[5]考慮彈性振動(dòng)和液體晃動(dòng)為外界干擾，采用魯棒觀測(cè)器設(shè)計(jì)了運(yùn)載火箭的姿態(tài)控制系統(tǒng)。薛宇等[6]考慮參數(shù)不確定性和外部干擾，采用魯棒控制理論設(shè)計(jì)火箭姿控系統(tǒng)，仿真結(jié)果表明，對(duì)參數(shù)不確定性具有良好的魯棒性。趙黨軍等[7]將自抗擾控制思想與微分代數(shù)結(jié)合，提出了一種新的自抗擾姿態(tài)控制器方法，提高了運(yùn)載火箭姿態(tài)控制系統(tǒng)的可靠性，但其使用的算法模型依然為標(biāo)稱軌跡下的小偏差線性化模型。此外，動(dòng)態(tài)逆控制[8]、滑模控制[9]、神經(jīng)網(wǎng)絡(luò)控制[10]和魯棒增益調(diào)度控制[11]等方法也被用于解決運(yùn)載火箭姿態(tài)系統(tǒng)的穩(wěn)定控制問題，但這些工作大多針對(duì)運(yùn)載火箭發(fā)射、大推力入軌和在軌飛行階段進(jìn)行研究，較少分析運(yùn)載火箭垂直著陸段的模型特性和性能需求。錢默抒等[12]針對(duì)運(yùn)載火箭一子級(jí)垂直著陸前的姿態(tài)調(diào)整階段，提出了一種基于滑模動(dòng)態(tài)面控制技術(shù)的垂直回收控制策略，可實(shí)現(xiàn)姿態(tài)角的非線性跟蹤控制。

本文將針對(duì)火箭一子級(jí)垂直著陸段的姿態(tài)控制問題展開研究，提出一種帶預(yù)設(shè)性能的姿態(tài)自適應(yīng)控制策略，能夠有效地解決外界環(huán)境干擾、參數(shù)不確定性以及系統(tǒng)未知?jiǎng)討B(tài)對(duì)系統(tǒng)的影響。該控制策略中，引入了誤差轉(zhuǎn)換技術(shù)，在對(duì)姿態(tài)角跟蹤誤差進(jìn)行系統(tǒng)變換后設(shè)計(jì)自適應(yīng)控制律，可滿足用戶預(yù)設(shè)的瞬態(tài)和穩(wěn)態(tài)性能需求，進(jìn)一步提高了運(yùn)載火箭姿態(tài)控制系統(tǒng)的可靠性和控制精度。

本文內(nèi)容安排如下：第一節(jié)建立了垂直著陸段火箭的姿態(tài)動(dòng)力學(xué)模型；第二節(jié)引入了誤差轉(zhuǎn)換技術(shù)，基于神經(jīng)網(wǎng)絡(luò)和自適應(yīng)方法設(shè)計(jì)了帶預(yù)設(shè)性能的姿態(tài)自適應(yīng)控制系統(tǒng)，并通過Lyapunov理論完成了對(duì)閉環(huán)系統(tǒng)的穩(wěn)定性分析；第三節(jié)通過開展數(shù)值仿真實(shí)驗(yàn)，充分驗(yàn)證了本文提出的控制方法的有效性和強(qiáng)魯棒性。

1 火箭姿態(tài)動(dòng)力學(xué)模型

定義箭體坐標(biāo)系為Oxyz，坐標(biāo)原點(diǎn)O為火箭質(zhì)心,z軸為箭體外殼對(duì)稱軸，方向沿箭體軸指向火箭頭部，與x，y軸構(gòu)成右手直角坐標(biāo)系。考慮運(yùn)載火箭為剛性箭體，其姿態(tài)動(dòng)力學(xué)方程可表示為

(1)

(2)

式中，sηsinη,cηcosη,tηtanη。τ∈R3為火箭柵格舵產(chǎn)生的控制力矩；M(T,δx,δy)為尾部發(fā)動(dòng)機(jī)推力矢量作用下產(chǎn)生的箭體偏轉(zhuǎn)力矩，在本文中假設(shè)偏轉(zhuǎn)力矩與發(fā)動(dòng)機(jī)推力大小T、發(fā)動(dòng)機(jī)擺角δx和δy成函數(shù)關(guān)系；同時(shí)，火箭飛行過程中燃料消耗和貯箱液體晃動(dòng)等因素將引起火箭箭體轉(zhuǎn)動(dòng)慣量的變化，記為ΔJ，其對(duì)應(yīng)產(chǎn)生的攝動(dòng)力矩可表示為MΔJ；Mext為氣流速度引起的氣動(dòng)力矩，考慮飛行環(huán)境中普遍存在不可測(cè)的風(fēng)速干擾，該氣動(dòng)力矩視作未知環(huán)境干擾。為方便表示，可定義dMΔJ+Mext為總未知干擾力矩。

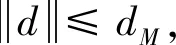
2 火箭姿態(tài)控制系統(tǒng)設(shè)計(jì)

2.1 控制目標(biāo)描述

本文的目的在于設(shè)計(jì)一種帶預(yù)設(shè)性能的自適應(yīng)控制算法，在未知環(huán)境干擾和未建模系統(tǒng)動(dòng)態(tài)同時(shí)存在的情況下，實(shí)現(xiàn)對(duì)火箭垂直著陸段飛行過程中期望姿態(tài)角ηd=[φd,θd,ψd]T的高精度跟蹤；同時(shí)，為保證飛行安全，火箭姿態(tài)角將始終被限制在預(yù)設(shè)的運(yùn)行范圍內(nèi)，表示為

(3)

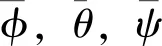
假設(shè)2期望姿態(tài)角軌跡ηd=[φd,θd,ψd]T和預(yù)設(shè)的姿態(tài)角上下界已知，均為關(guān)于時(shí)間連續(xù)可導(dǎo)的光滑函數(shù)。

2.2 誤差轉(zhuǎn)換

定義姿態(tài)角跟蹤誤差為

eη[eφ,eθ,eψ]T=η-ηd

(4)

結(jié)合式(3)可得到

(5)

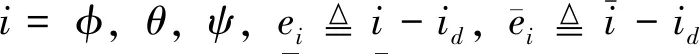
為實(shí)現(xiàn)預(yù)設(shè)的控制性能，本文引入誤差轉(zhuǎn)換技術(shù)將上述原始的受約束跟蹤誤差信號(hào)(約束誤差信號(hào)需保持在預(yù)設(shè)的誤差上下界內(nèi))轉(zhuǎn)換為一個(gè)新的不受約束的誤差信號(hào)。誤差轉(zhuǎn)換函數(shù)可表示為

(6)

式中，si∈R為轉(zhuǎn)換后誤差，Zi(·):R×R×R→R為用戶自定義的隨ei嚴(yán)格遞增的光滑函數(shù)，即?si/?ei>0。同時(shí)，該函數(shù)滿足

(7)

可以判斷，若轉(zhuǎn)化后的誤差si有界，則原始誤差ei有界，且始終維持在預(yù)設(shè)的誤差域內(nèi)。因此，上述控制目標(biāo)轉(zhuǎn)化為尋找合適的控制律，以保證誤差信號(hào)si是有界的。

本文中，選取如下誤差轉(zhuǎn)換函數(shù)

(8)

式中，ln(·)為自然對(duì)數(shù)函數(shù)，Z0∈R+為正實(shí)數(shù)。

接下來，需要進(jìn)一步獲取經(jīng)轉(zhuǎn)換后新的誤差動(dòng)態(tài)。總寫式(6)為

(9)

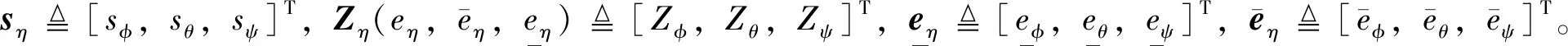
并進(jìn)行如下定義

(10)

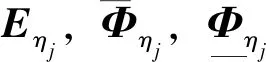
接著，對(duì)公式(9)中的姿態(tài)轉(zhuǎn)換誤差依次求時(shí)間微分可得到

(11)

式中

(12)

進(jìn)一步對(duì)式(11)求時(shí)間微分有

(13)

式中

(14)

類似的，上述公式中Mη1和Mη2可通過計(jì)算得到。

接著，定義濾波跟蹤誤差為

(15)

式中，λη∈R+為正實(shí)數(shù)。

結(jié)合式(1)求解上述濾波跟蹤誤差rη的時(shí)間微分，可得到

(16)

2.3 神經(jīng)網(wǎng)絡(luò)補(bǔ)償器

針對(duì)火箭姿態(tài)動(dòng)力學(xué)(1)中的未知系統(tǒng)動(dòng)態(tài)M(T,δx,δy)，本文引入一個(gè)三層的神經(jīng)網(wǎng)絡(luò)加以補(bǔ)償。神經(jīng)網(wǎng)絡(luò)的輸出可表示為

(17)

M(T,δx,δy)=W*Tφ(VTX)+ε

(18)

式中，W*∈Rn×3為輸出層的理想權(quán)重矩陣，ε為對(duì)應(yīng)的函數(shù)逼近誤差。如果隱含層的權(quán)重隨機(jī)初始化并且在隨后的學(xué)習(xí)過程中保持不變，通過增加隱含層節(jié)點(diǎn)個(gè)數(shù)n，可使得逼近誤差ε足夠小。此外，考慮隱含層權(quán)重V在學(xué)習(xí)過程中保持不變，在下文的敘述中將予以省略。

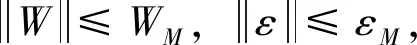
2.4 姿態(tài)控制器設(shè)計(jì)

本文針對(duì)運(yùn)載火箭垂直著陸段飛行的自適應(yīng)姿態(tài)控制器設(shè)計(jì)為

(19)

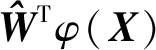
(20)

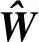
(21)

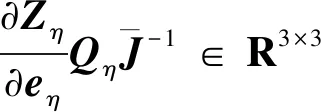
(22)

式中，μ∈R+為正實(shí)數(shù)。

本文所設(shè)計(jì)的姿態(tài)控制算法的穩(wěn)定性由以下定理給出。

定理1考慮公式(1)所描述的運(yùn)載火箭垂直著陸段姿態(tài)動(dòng)力學(xué)模型，當(dāng)假設(shè)1～3成立時(shí),如果選擇姿態(tài)控制器(19)，以及自適應(yīng)律(20)和(22)，可以保證姿態(tài)角跟蹤誤差eη漸進(jìn)趨于零點(diǎn)，且閉環(huán)系統(tǒng)其他信號(hào)始終有界。

證明：構(gòu)造Lyapunov函數(shù)為

(23)

對(duì)V求時(shí)間微分可得到

(24)

將公式(16)和(18)代入式(24)有

(25)

接著，代入姿態(tài)控制器(19)，式(25)可寫作

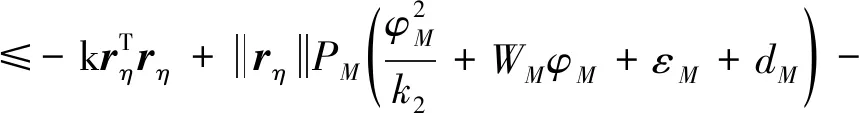
(26)

考慮下式始終成立

(27)

則公式(26)可計(jì)算為

(28)

進(jìn)一步，將自適應(yīng)律(22)代入式(28)，得到

(29)

對(duì)式(29)兩邊同時(shí)取時(shí)間積分有

(30)

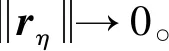
3 仿真驗(yàn)證

3.1 仿真參數(shù)設(shè)置

仿真中采用的運(yùn)載火箭總體參數(shù)如表1所示。

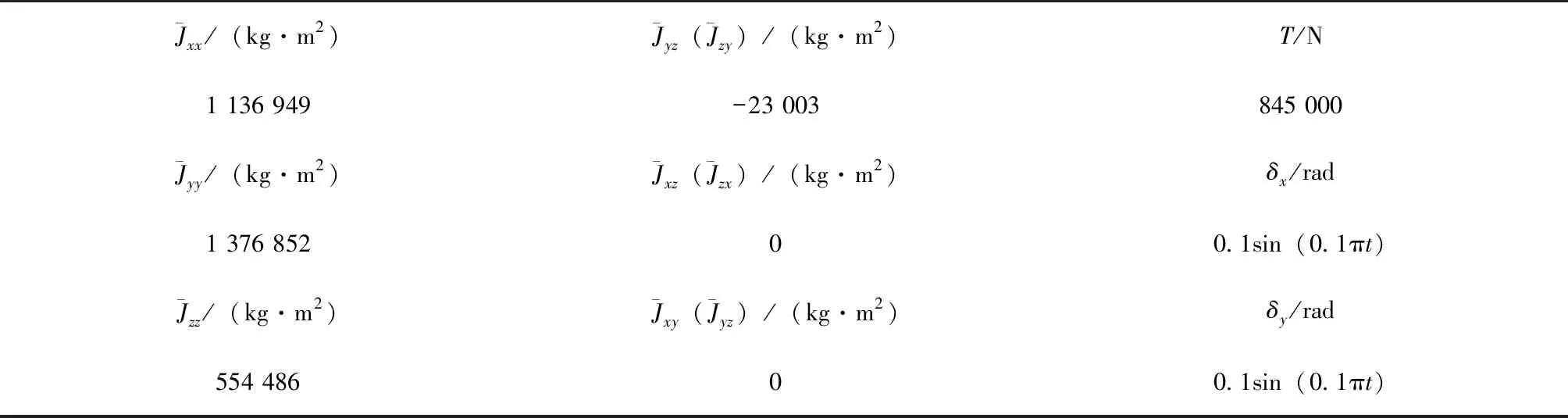
表1 仿真參數(shù)

垂直著陸段飛行的各初始姿態(tài)角選擇如下

φ(0)=31.51°,θ(0)=20.05°,ψ(0)=2.86°ωx(0)=ωy(0)=ωz(0)=0(rad/s)

(31)

仿真中姿態(tài)控制器各控制參數(shù)選擇為

k=200,k1=k2=λη=2,μ=300

(32)

待更新參數(shù)初始值設(shè)置為

(33)

未知?dú)鈩?dòng)干擾力矩在仿真中設(shè)定為

Mext=104×

[sin(0.1πt),sin(0.2πt),cos(0.1πt)]T(N·m)

(34)

垂直著陸段飛行中的慣性參數(shù)攝動(dòng)為

(35)

尾部發(fā)動(dòng)機(jī)推力矢量作用下產(chǎn)生的偏轉(zhuǎn)力矩假定為

M(T,δx,δy)=

T[-sin(δx),sin(δy)cos(δx),0]T(N·m)

(36)

為充分驗(yàn)證所設(shè)計(jì)的姿態(tài)自適應(yīng)控制算法的有效性，本文將給出上述外部干擾和未知系統(tǒng)動(dòng)態(tài)均存在下的火箭垂直著陸段的姿態(tài)跟蹤控制仿真。

3.2 仿真結(jié)果和分析

考慮未知?dú)鈩?dòng)干擾力矩Mext、發(fā)動(dòng)機(jī)推力矢量帶來的未知偏轉(zhuǎn)力矩M(T,δx,δy)以及燃料消耗帶來轉(zhuǎn)動(dòng)慣量變化ΔJ引起的干擾力矩同時(shí)存在于運(yùn)載火箭垂直著陸段的飛行過程中。分別設(shè)計(jì)PD控制器和上文中自適應(yīng)控制器，在給定參考姿態(tài)軌跡和預(yù)設(shè)控制性能下，各姿態(tài)角響應(yīng)曲線如圖1～圖3所示。

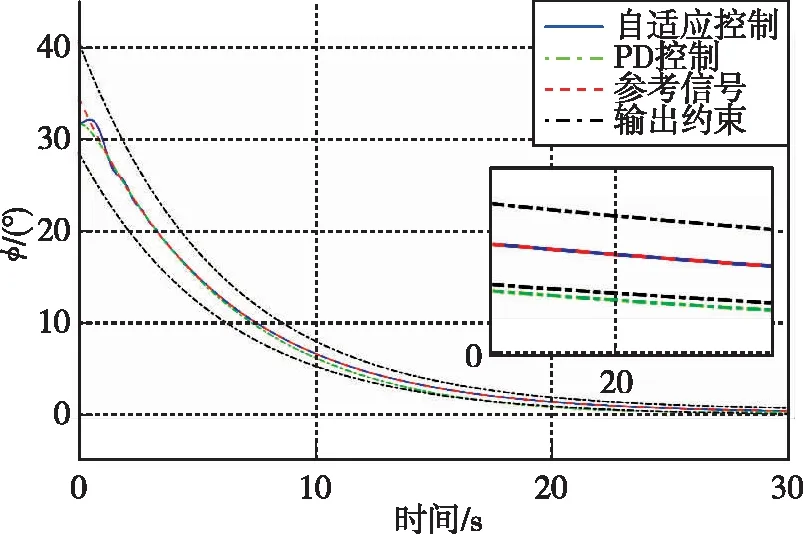
圖1 時(shí)間-滾轉(zhuǎn)角變化曲線Fig.1 Time history of roll angle

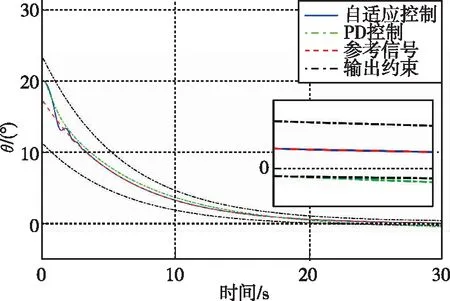
圖2 時(shí)間-俯仰角變化曲線Fig.2 Time history of pitch angle

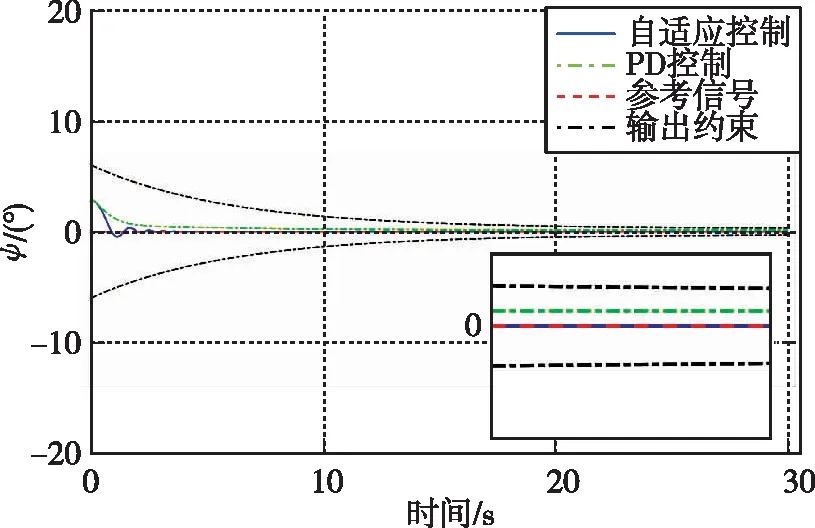
圖3 時(shí)間-偏航角變化曲線Fig.3 Time history of yaw angle

由各姿態(tài)角隨時(shí)間的響應(yīng)曲線可知，在外部干擾、模型不確定性同時(shí)存在的情況下，相比于PD控制器，本文提出的自適應(yīng)控制方法能在短時(shí)間內(nèi)實(shí)現(xiàn)對(duì)預(yù)定姿態(tài)軌跡的穩(wěn)定跟蹤，具有更強(qiáng)的魯棒性。同時(shí)，通過自定義姿態(tài)角跟蹤誤差的的上、下界，可使得姿態(tài)軌跡始終處于預(yù)設(shè)范圍內(nèi)，而PD控制器下則無法實(shí)現(xiàn)該性能。本文所設(shè)計(jì)的帶預(yù)設(shè)性能的姿態(tài)控制器一方面可以用于改善火箭姿態(tài)控制系統(tǒng)的瞬態(tài)響應(yīng)性能，另一方面可以保證其穩(wěn)態(tài)性能。以本文的仿真算例為例，通過預(yù)設(shè)姿態(tài)角跟蹤誤差的上、下界函數(shù)，系統(tǒng)穩(wěn)態(tài)誤差將始終小于0.3°，這充分顯示出本文設(shè)計(jì)的自適應(yīng)姿態(tài)控制算法的高穩(wěn)態(tài)精度。

4 結(jié)論

針對(duì)可重復(fù)使用運(yùn)載火箭復(fù)雜非線性和強(qiáng)不確定性等動(dòng)力學(xué)特性，基于自適應(yīng)控制技術(shù)設(shè)計(jì)了火箭垂直著陸段飛行的姿態(tài)控制方法。同時(shí)，引入誤差轉(zhuǎn)換技術(shù)，實(shí)現(xiàn)用戶預(yù)設(shè)的控制性能。研究表明，本文設(shè)計(jì)的帶預(yù)設(shè)性能的自適應(yīng)控制算法能實(shí)現(xiàn)對(duì)預(yù)定姿態(tài)軌跡的穩(wěn)定跟蹤，閉環(huán)系統(tǒng)具有良好的瞬態(tài)和穩(wěn)態(tài)性能，且對(duì)外部干擾和模型不確定性具有強(qiáng)適應(yīng)性。