基于兩種方法的鐵路隧道棄渣場抗滑穩定性分析

鄭良靜

(中鐵二十一局集團有限公司 甘肅蘭州 730070)

1 前言

隧道棄渣場一般由開挖隧道所排出的松散土體、碎石等物質組成，具有非飽和、欠密實、多孔隙等結構特點；強度較低，容易產生滑坡等地質災害，對其下方建筑物、公用設施以及居民的生命財產安全等都存在著巨大威脅[1]。棄渣堆積體穩定性主要受堆積體幾何形態、物理力學性質和下伏基巖產狀及物理力學性質、地表水及地下水等因素影響。穩定分析方法主要有工程地質法、傳統極限分析法以及數值極限分析法[2]。

通常邊坡穩定的安全系數與滑動面位置關系密切[3]，張昊[4]等以均質邊坡為例采用強度折減法計算分析了邊坡穩定過程中安全系數和滑動面之間的關系。李建朋[5]等基于臨界狀態速度場的分析，提出了一種新的邊坡臨界狀態滑動面確定方法。

隧道棄渣堆積體多孔多相不均勻，結構松散欠密實，傳統方法在確定破壞面形態方面存在困難[6]。劉建偉[7]等通過采集測定坡面不同位置處棄渣容重、含水量、飽和導水率、飽和含水量、砂粒含量、碎石含量等物理指標和直剪試驗，分析了棄渣場邊坡穩定性特征。楊華清[8]以云南省華麗高速26號合同段棄渣場為例研究了粒組級配、最終堆積形態及棄渣場穩定的關系。數值計算方面，田永鑄[9]針對中南部鐵路通道沿線某一黃土隧道棄渣場，通過現場勘查及已有相關資料，結合室內外土工試驗，運用理論分析方法，對該棄渣場的穩定性進行計算與分析。毛雪松[10]等以某新近堆積棄渣場為例，采用非飽和滲流研究方法，基于GeoStudio軟件中的SEEP/W和SLOPE/W模塊對其滲流場及不同工況下的穩定性進行分析。孫朝燚[11]等通過現場地質調查和區域劃分，借助基于強度折減法的有限元軟件分析棄渣場邊坡穩定性和潛在破壞機制，以此研究棄渣場走向夾角對其潛在破壞機制的影響。本文以新建鐵路敦格線闊克薩隧道棄渣場為例，介紹一種較為實用且穩妥的計算棄渣場抗滑穩定安全系數的方法。

2 工程概況

新建鐵路敦格線闊克薩隧道段區域隸屬于甘肅省阿克塞縣，隧道洞身穿過當金山脈。闊克薩隧道棄渣場位于闊克薩隧道出口DIK191＋600右側荒溝內。棄渣場設計棄渣量約4.87萬m3，占荒溝9.57畝。棄渣場前緣高度約為8 m，坡度約45°，棄渣堆坡頂平臺寬度約為43 m。坡腳采用擋墻防護，擋墻高8 m，基礎埋深2 m。擋墻頂部設置一個寬為10 m的平臺，棄渣堆邊坡前緣無人員活動場所和設施，至2019年邊坡已穩定存在五年。

棄渣場平均海拔約2 858 m，最高海拔2 888 m。棄渣場所在區域為中溫帶干旱氣候區，降水量小，蒸發量大，冬冷夏熱，空氣干燥。年平均氣溫3.1℃，年平均降水量127 mm，年平均蒸發量3 297.9 mm。土壤最大凍結深度235 cm。棄渣場范圍未見地表水，偶見有積雪融水，隧道洞身及附近未見地下水出露。地下水類型為第四系潛水及基巖裂隙水，補給主要靠大氣降水及地表徑流，排泄以蒸發和地下徑流為主。

闊克薩隧道棄渣以斷層角礫、碎裂巖為主。斷層角礫呈灰白色、青灰色，尖棱狀～棱角狀，成分以石英片巖為主，粒徑2～20 mm的含量約為50%，20～60 mm的占5% ～15%，粉土、砂土充填，局部可見輕微泥砂質膠結，角礫手可捏碎，夾斷層泥，稍濕，密實；碎裂巖呈棕紅色，原巖為泥巖夾礫巖，成分以黏土礦物為主，洞身段碎裂巖為灰黑色、青灰色，表面局部呈銹黃色，原巖為石英片巖，成分以石英、云母等為主，巖質受構造影響破碎不均，局部呈巨塊狀，大部呈碎石狀、角礫狀。

棄渣場地基為粉土，灰黃色，土質不均，含少量礫石，表層含植物根系，稍濕。

3 棄渣場邊坡穩定性分析

棄渣場抗滑穩定性計算一般采用瑞典圓弧法，對于均質渣體推薦使用簡化畢肖普法，對于有軟弱夾層的渣場，宜采用摩根斯頓-普賴斯(M-P)法計算[12]。本棄渣場棄渣組分多元，為非均質渣體。為保證計算分析的可靠性，首先采用強度折減法進行邊坡穩定性分析，確定臨界滑動面形態，然后采用傳統極限平衡法中的M-P法計算典型剖面的安全系數，并將二者計算結果進行比較。

3.1 計算工況

本棄渣場場地所在位置處于Ⅵ度烈度區，依據規范不需要考慮地震對棄渣場穩定性的影響。同時本地區屬于典型的干旱地區(年降雨量不足200 mm)，且淺層無地下水分布，也無需考慮滲流工況或降雨工況下的邊坡穩定性。因此，計算工況僅需考慮采用自然狀態下巖土體物理力學參數分析棄渣場邊坡穩定性。

3.2 計算坡面選取

根據現場實地測量，形成棄土堆坡面三維地形圖，并選取坡度最大截面為穩定性分析的計算剖面。剖面尺寸見圖1。

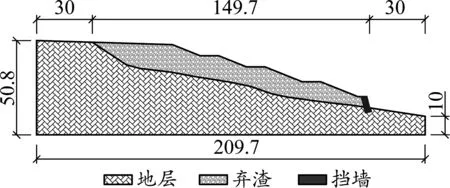
圖1 計算剖面(單位:m)

闊克薩隧道棄渣場實際棄渣量約5萬m3，最大堆渣高度約38 m，渣場失事對主體工程或環境造成的危害程度較輕，判別該棄渣場為4級棄渣場，計算參數如表1所示。

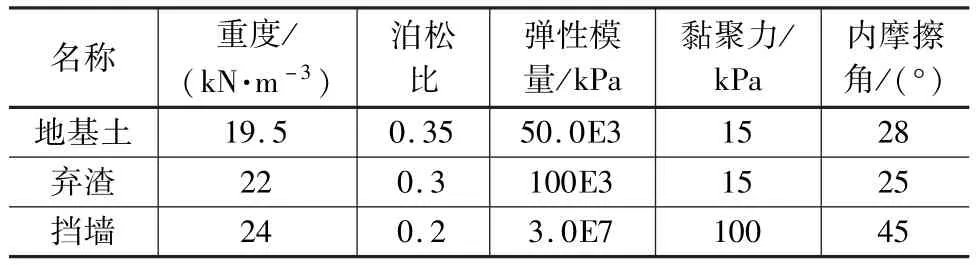
表1 巖土體及擋墻物理力學參數

3.3 強度折減法計算模型及分析結果

計算模型如圖2所示，整個模型共劃分4 996個單元，其中地層3 615個單元，棄渣堆1 352個單元，擋墻29個單元，均采用平面應變CPE4單元。土體和擋墻均采用摩爾-庫倫模型，為防止滑動面穿過擋墻，擋墻混凝土材料的黏聚力和內摩擦角取較大數值。棄渣堆與地層邊界采用非光滑面-面接觸，棄渣堆與擋墻邊界采用Tie連接，地層與擋墻部分邊界采用非光滑面-面接觸，部分采用Tie連接。外部邊界條件如圖2所示。

塑性變形云圖見圖3。可以看出，當強度折減系數為1.504時，擋墻處開始出現較大塑性應變，整個擋墻在墻后邊坡的擠壓作用下發生繞墻踵的轉動位移，導致墻后及墻趾處塑性變形較大；當強度折減系數增大到1.642時，塑性區范圍進一步擴大，滑動面尚未形成，但可見其繞過擋墻根部，由墻踵出發，逐漸向墻后棄渣堆積體內部發展，如圖4所示；當強度折減系數進一步增大到1.678時，塑性區擴展到棄渣堆積體第一級平臺頂部，從而在渣堆內部形成了一條貫通的滑動面，如圖5a所示。

圖2 有限元計算模型

圖3 塑性應變云圖(折減系數＝1.504)

圖4 塑性應變云圖(折減系數＝1.642)

圖5 塑性應變云圖(折減系數＝1.678)

由圖5b可見，擋墻前側、墻蹱處以及墻背土體均出現塑性區，且墻背塑性區呈倒三角形，表明擋墻既有平動位移也發生了轉動位移。渣堆體下部滑動明顯，越往上，變形逐漸減小。

計算結果表明，當折減系數為1.642時(見圖6)，擋墻頂部水平位移出現突增，即強度折減系數取為1.642時，邊坡處于臨界平衡狀態。表明棄渣場邊坡具有一定的強度儲備。

圖6 擋墻頂部水平位移(U1)隨折減系數的變化

3.4 極限平衡法計算模型及分析結果

基于強度折減的有限元法結合彈性數值分析進行邊坡穩定性評估，具有較高精度，但數值分析不能獲得巖土的破壞狀態與破壞面，因而無法求出極限荷載與穩定安全系數[12]。采用傳統極限平衡法計算出臨界滑動面的穩定安全系數，但是確定具有最小安全系數臨界滑動面的位置是極限平衡法的關鍵。臨界滑動面的位置及形態與地層分布、渣堆體及地層的物理力學性質等諸多因素有關，很難通過搜索確定可信的臨界滑動面。如果將基于強度折減的數值法與基于極限平衡的傳統分析法結合起來，就可以確定出破壞面，也可以求出穩定安全系數。

傳統的極限平衡法計算模型采用相同的物理力學參數和幾何尺寸，模型如圖7所示。根據強度折減法分析的破壞面形態和位置，在極限平衡法中采用指定滑動面入口和出口的方式搜索臨界滑動面，滑動面為圓弧面，條間力函數采用半正弦函數，分析結果安全系數為1.777。臨界滑動面形態見圖8，可見與強度折減法計算結果大體相近。根據規范，4級棄渣場正常運用抗滑穩定安全系數須大于1.2，因此可判定該邊坡抗滑穩定性滿足規范要求。

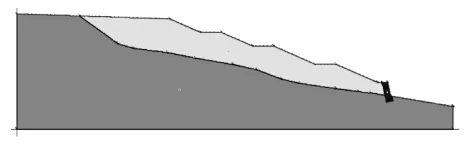
圖7 極限平衡法計算模型

圖8 臨界滑動面形態

采用M-P法收斂情況如圖9所示。M-P法通過引入系數λ和條間力函數建立條間豎向力和水平力之間的約束關系，使得靜力平衡方程完備。當λ＝0時，M-P法力矩平衡退化為簡化Bishop法(對應的安全系數為1.774)，力平衡退化為簡化Janbu法(對應的安全系數為1.646)。

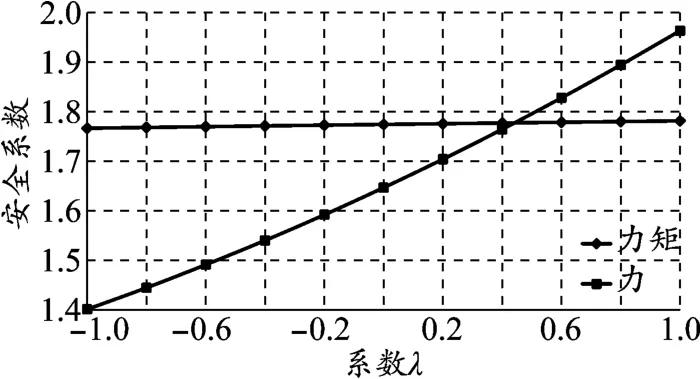
圖9 安全系數隨λ變化情況

4 結束語

綜上所述，規范推薦采用傳統極限分析法求解棄渣場穩定安全系數，但由于棄渣堆積體通常成分復雜，傳統方法并不能完全適應，特別是在臨界滑動面的位置和形態確定方面存在困難。因此對于棄渣場邊坡抗滑穩定問題，建議首先應用基于強度折減法的有限元分析初步確定破壞面形態，然后根據破壞面的形態利用傳統方法求解穩定安全系數。