基于改進支持向量機回歸的非線性飛機結構載荷模型建模

唐寧，白雪

(中國飛行試驗研究院 飛機所， 西安 710089)

0 引 言

飛機結構載荷測量是驗證飛機結構強度設計、實施飛行安全監控及飛機疲勞壽命估算的重要手段，國軍標及相關適航條例均對此做出了具體要求[1-2]。目前，通常采用應變法對飛機結構載荷進行測量，該方法通過地面校準試驗建立結構載荷-應變模型，并在此基礎上通過飛行實測應變得到真實飛行環境下的飛機結構載荷。該方法的關鍵在于結構應變測量，但應變電橋在使用中存在使用壽命限制，并且可能會遭受無法修復的意外損壞，從而導致無法進行長期可靠的載荷測量。因此，有必要在應變法所測量飛機結構載荷的基礎上發展一種基于飛機飛行參數的飛機結構載荷模型。采用該模型，可對同一型號多架飛機在無需進行應變改裝及校準試驗的情況下，實施載荷監控及結構強度分析，并為飛機疲勞壽命評估積累相關數據。

飛機結構在真實飛行過程中同時受到氣動力、慣性力及約束力影響，其中約束力即所測量的飛機結構載荷。根據達朗貝爾原理[3]，三者合力恒為零，即飛機結構載荷取決于飛機結構所受氣動力及慣性力，其中慣性力與結構重力及其過載線性相關；而氣動力在低馬赫數及小迎角情況下與飛行迎角及動壓呈線性關系，但在高馬赫數或大迎角條件下，該線性關系并不存在，氣動力呈現較為復雜的非線性特征[4]。在該條件下，可通過空氣動力學及飛行力學理論方法建立基于飛行參數的非線性飛機結構載荷模型，但實現難度較高，而以人工神經網絡和支持向量機為代表的基于數據的非線性建模方法可在已知相關飛行參數及其對應結構載荷數據的情況下進行建模。目前，國內外已在該領域開展了相關研究工作[5-7]，其中神經網絡模型具有較好的適應性及非線性特征，但建模過程中網絡結構的確定并無明確方法且模型對樣本敏感，存在過擬合問題[8]；而支持向量機回歸(SVR)方法則較好地避免了上述問題，該方法數學理論基礎完善，具有較強的魯棒性，在引入核函數的條件下具有較好的非線性建模能力，基于該方法的建模工作研究已于眾多領域開展[9]。因此，針對基于飛行參數的飛機結構載荷建模問題，可在SVR方法的基礎上展開應用研究。

本文在原始SVR方法基礎上，通過改進序列最小優化(Sequential Minimal Optimization，簡稱SMO)算法及基于粒子群算法的模型參數優選方法得到一種飛機結構載荷模型的建立方法，并以某型飛機跨聲速俯仰對稱機動為例進行該建模方法的仿真驗證計算。

1 飛機結構載荷SVR模型建立

飛機在飛行過程中的結構載荷包含關鍵部位的彎矩、剪力、扭矩及拉壓力等，而結構載荷受飛行高度、速度、迎角、側滑角、舵面偏角、各向角速度及過載等眾多因素影響。建立飛機結構載荷模型的目的是使用SVR方法基于飛行實測載荷及飛參數據準確建立表述結構載荷與重要飛行參數之間關系的非線性模型。

1.1 模型輸入變量確定

飛機飛行過程中所記錄的飛行參數種類較多，如果將所有參數均作為飛機結構載荷模型的輸入變量，首先會因變量過多，樣本容量過大而降低運算速度；其次，過多的變量類型中必然包含冗余變量，會對模型精度造成不利影響。因此，在構建模型過程中，應明確與模型輸出有較好相關性的輸入變量，以保證模型精度及效率。

為確定有效輸入變量，首先應依據空氣動力學及飛行動力學理論定性地對飛機進行動力學分析，得到影響飛機姿態及運動狀態的主要參數，例如速度、高度、迎角、舵面偏角等，以初步確定輸入變量。在此基礎上，對于輸入變量與輸出變量之間的相關性，采用兩者間的皮爾遜相關系數R(X,Y)進行量化判定，其表達式如下[10]

(1)

式中：cov(X,Y)為兩變量的協方差；var(X)、var(Y)分別為變量方差，其取值范圍為[-1,1]。

|R|越大，則兩變量間相關性越強，一般以|R|是否大于0.7判斷兩變量間是否具有較強相關性，取具有強相關性的參數作為建模參數可保證所建立的模型精度不受冗余參數影響。

1.2 SVR方法基本原理

回歸是研究變量間函數關系的一種方法[11],其目的是通過相應估算方法得到給定的訓練樣本集xi∈Rn,yi∈R(i=1,…,l)之間的回歸方程：

f(x)=ωTk(x)+b

(2)

式中：ω為回歸參數向量；函數k為非線性回歸中對樣本在高維空間中的非線性映射。

傳統回歸模型一般通過模型輸出f(x)與真實輸出y之間的差別來計算精度損失，而SVR模型則以f(x)為中心，構建寬為2ε的間隔帶，訓練樣本在此間隔帶內則認為預測正確，不計入損失，該方法保證了模型的魯棒性。基于損失最小的原則，SVR問題在支持向量機(SVM)問題的基礎上形式化為[12]

(3)

式中：C為正則化常數；lε為不敏感損失函數，當訓練樣本落入間隔帶內時該值為0，否則計入損失。

損失為

loss=|f(xi)-yi|-ε

(4)

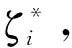
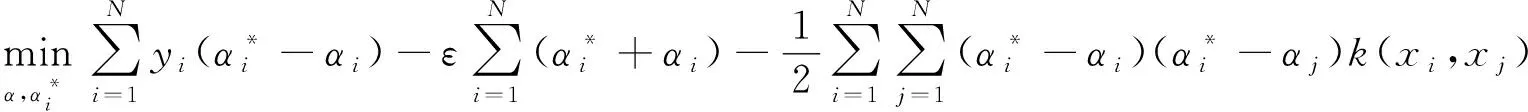
(5)

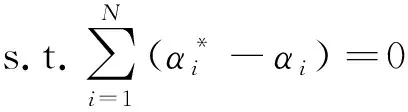
0≤αi≤C

其中k(xi,xj)=φ(xi)Tφ(xj)為核函數，采用核函數可簡化低維空間樣本點映射到高維空間的運算，是該方法可進行非線性回歸的關鍵因素。求解式(5)優化問題，可得SVR問題解的形式為

(6)

2 飛機結構載荷SVR模型訓練算法

SMO算法是針對SVR問題的快速學習算法[14]，在樣本容量較大時，其效率高于傳統凸二次規劃問題求解算法，該算法包括兩部分：啟發式雙變量選擇和變量解析計算。以下將給出該算法實現的主要步驟，并對其進行改進，以進一步提升效率。

2.1 啟發式雙變量選擇

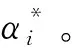
對式(5)進行變量替換：

(7)

則式(5)可寫為

(8)

首先對(-C,C)區間內的訓練樣本點進行遍歷，選擇違反KKT條件最嚴重的點作為第一個變量；若該區間內不存在違反KKT條件的點，則以相同方法對區間邊界樣本點進行檢驗；若仍不存在這樣的樣本點，則已得到問題的最優解，程序結束。

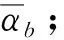
2.2 變量解析運算

(9)

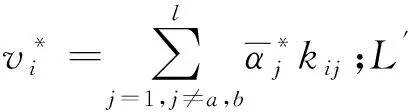
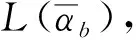
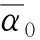
2.3 SMO算法改進

雖然SMO算法可實現SVR問題的高效求解，但實踐表明，僅以KKT條件為停機準則過于嚴格，使得訓練時間較長，而模型在訓練到一定程度時已滿足精度要求，因此有必要基于停機準則對SMO算法進行改進以提高建模效率。

根據對偶問題(式(8))與原始問題(式(2))的關系，當對偶問題與原始問題對偶間隙為0時，所得的對偶問題解為原始問題的全局最優解，因此當對偶間隙小于給定閾值時，即可認為已得到目標解，可停止建模計算。在此基礎上對SMO算法進行改進，具體方法如下：

(10)

則原始問題的目標函數可寫為

(11)

(12)

當σ小于指定值時則停止模型訓練。因此，定義如下三個停機條件：①所有變量滿足KKT條件；②σ小于指定值；③迭代循環次數到達制定上限。當上述任一停機條件達到時，均停止建模，以此提升SMO算法效率。

3 飛機結構載荷SVR模型參數優化

SVR模型參數包括正則化常數C及核函數K的相關參數，模型參數選擇的合理性會直接影響模型精度及計算效率，但SVR方法并未提供模型參數優選方法，一般為任意給定或通過經驗給定。本文采用粒子群優化(PSO)算法[15]對飛機結構載荷SVR模型參數進行優化選取。

PSO算法假設待優化變量處于范圍給定的D維搜索空間內，由n個粒子組成粒子群X=(X1,X2,…,Xn)，其中每個粒子均為D維向量，是該粒子在搜索空間中的位置，同時也是原始優化問題的潛在解。依據優化目標函數可計算出每個粒子的適應度，并依此判斷目標優化情況。在迭代過程中，為使粒子群向優化目標運動，定義第i個粒子的速度Vi=[Vi1,Vi2,…,ViD]，并定義單個粒子在尋優過程中的極值變量Pi=[Pi1,Pi2,…,PiD]，整個粒子群極值變量Pg=[Pg1,Pg2,…,PgD]。在迭代過程中，粒子通過Pi和Pg更新Vi及X，更新方法為

(13)

式中：ρ為慣性權重常數；c1和c2為非負的加速度因子常數；r1和r2為[0,1]之間的隨機數。

當迭代次數達到最大限制或連續多次適應度函數迭代結果保持不變時，則停止計算。

采用PSO算法對飛機結構載荷SVR模型相關參數進行優選，定義適應度函數F為模型的平均誤差，其形式為

(14)

式中：f(xi)為第i個樣本點的計算值；yi為與之對應的樣本目標值。

每組模型參數對應單個粒子，其優化目標是得到使適應度函數最小的SVR模型參數。由此，采用PSO算法優化的飛機結構載荷SVR模型建立方法如圖1所示。

圖1 建模流程

4 方法驗證及結果分析

以某型飛機在基本飛行重量且無外掛構型下跨聲速俯仰對稱機動過程中機翼某一測載剖面處結構剪力實測數據為原始數據，采用上述改進支持向量機回歸方法進行建模，為確保所建立模型的泛化能力得到檢驗，未對正負過載進行區分，取36個法向過載較小的俯仰機動數據作為建模數據集，9個法向過載較大的俯仰機動數據作為測試數據集。建模前對原始實測數據進行清零、去跳點及各參數時間統一性檢驗等預處理工作。

4.1 建模參數確定

飛機在對稱俯仰機動過程中，繞質心運動為其主要運動形式，運動中飛機除受自身轉動慣量Iy影響外，還受到翼身氣動力矩Mwb、平尾氣動力矩Mt、俯仰阻尼力矩Mq及洗流時差力矩Mα等外部因素影響。根據空氣動力學理論，上述外力矩的主要影響飛行參數包括氣壓高度H、指示空速V、迎角α、升降舵或全動平尾偏度δe、俯仰角速度q及其他可對飛機氣動力產生影響的舵面偏度。在機動過程中，飛機會形成法向過載，這是俯仰機動的主要特征。初步將上述參數確定為主要建模參數，對剖面結構剪力與上述參數的相關性進行分析，相關系數計算結果如表1所示。

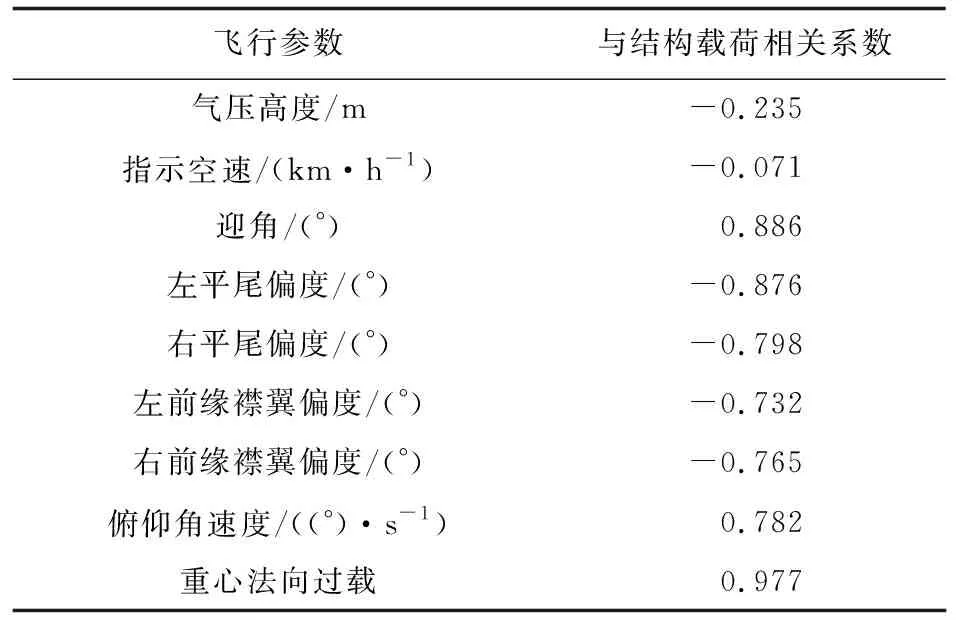
表1 相關性計算結果

從表1可以看出：氣壓高度及空速與結構載荷的相關系數很小，表明其在機動過程中與機翼結構載荷相關性并不強，究其原因，雖然它們是決定氣動力的關鍵因素，但建模采用俯仰機動過程數據，在該時間段內飛機高度和速度基本保持不變，而實測結構載荷隨機動過程必然產生相應變化，因此兩參數與載荷間呈現低相關性是合理的，故在給定飛機狀態俯仰機動結構載荷建模中不將其作為建模參數；而根據空氣動力學理論，該過程中引起氣動力改變的主要因素是迎角，相關系數計算結果也證明了這一點。

對于參與建模的參數，因其量級差異較大，在開始建模前，為保證后續建模工作的計算效率，需對其進行歸一化處理。針對各參數，在飛行實測中均有對應的測量范圍[Ximin,Ximax]，故歸一化方式為

(15)

4.2 模型建立及檢驗

在確定建模參數并對其進行歸一化的基礎上，采用改進支持向量機回歸方法建立飛機結構載荷模型，選擇高斯核函數作為核函數，其表達式為

(16)

給定支持向量機回歸間隔帶半帶寬ε為0.05，σ的臨界值為0.001，因此PSO算法需要確定的參數為正則化常數C和核函數參數γ，搜索空間為二維空間。設定粒子群中粒子數量為50，最大迭代數為100，采用圖1所示算法，使用建模數據集進行建模，每代最優個體適應度如圖2所示，根據迭代結果確定C=30.476，γ=3.223。

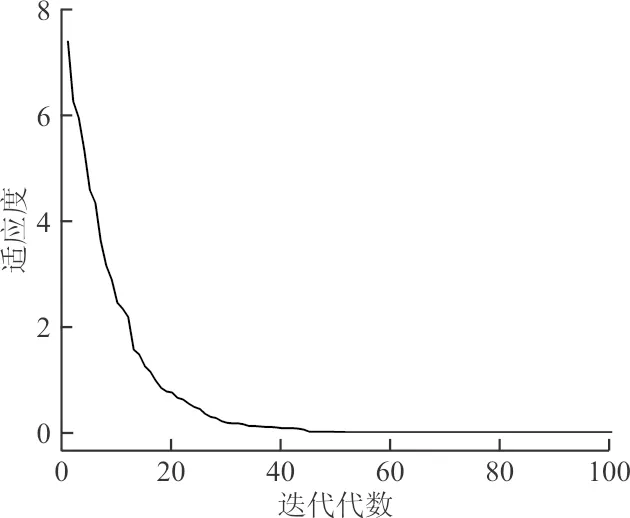
圖2 個體適應度迭代結果

作為對比，采用網格搜索及原始SVR方法對參數C、γ進行尋優，尋優目標仍為平均誤差(式(14))，尋優過程如圖3所示，目標仍為使誤差最小的參數組合。受計算時間限制，C的變化步長為1，γ的變化步長為0.1，最終確定C=32，γ=3.5。

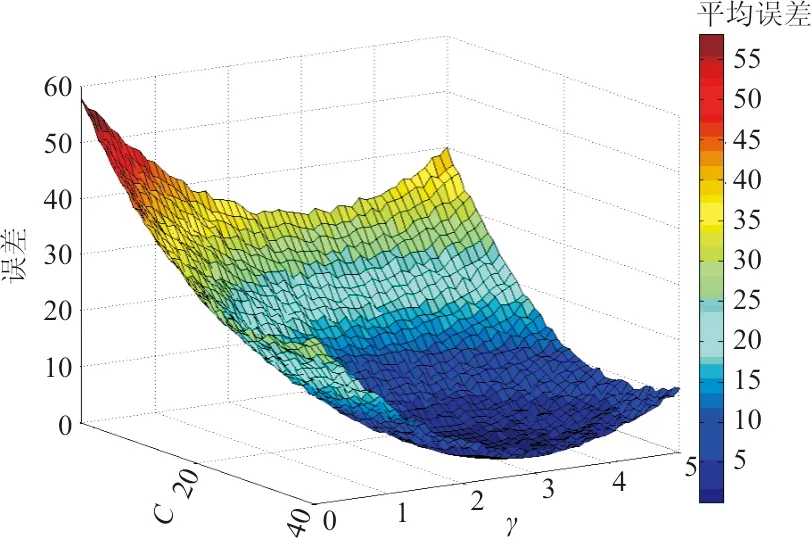
圖3 網格搜索法誤差

分別使用兩組C和γ進行建模計算, 并使用測試數據集對所建立的模型進行測試，結果如圖4所示。

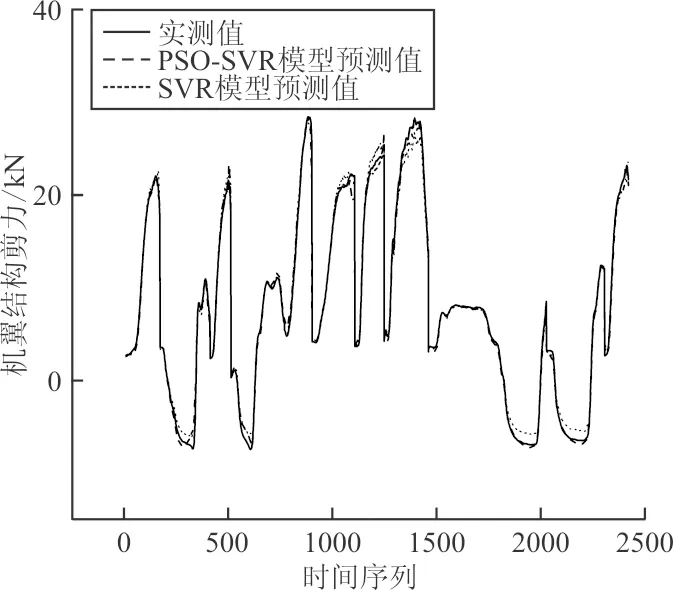
圖4 模型預測結果與載荷實測值對比

基于原始SVR算法與改進后的SVR算法的模型計算結果對比如表2所示，模型訓練精度及測試精度均使用平均誤差(式(14))進行評價。

表2 模型精度對比

從表2可以看出：基于改進SVR算法的飛機結構載荷模型與原始SVR算法模型相比，雖然訓練精度相差不大，但測試精度明顯優于后者，證明通過模型參數優選可提高模型泛化能力，并且建模過程中參數尋優速度明顯優于原始SVR算法，因此改進SMO算法停機條件并通過PSO算法優化模型參數是有必要的。

5 結 論

(1) 通過改進支持向量機回歸方法可獲得精度較高的非線性飛機結構載荷模型，相較于原始支持向量機算法，該方法建模效率高，且所得到的模型泛化能力較強，可更為準確地對飛機結構載荷進行預測。

(2) 通過建立泛化能力較好的飛機結構載荷模型，可對同一型號多架飛機進行結構載荷監控及結構疲勞壽命評估數據積累，對飛行數據進行深層次挖掘。

(3) 采用改進支持向量機方法所建立的基于試飛數據的飛機載荷模型避免了采用空氣動力學及飛行動力學理論進行建模所需的復雜理論推導工作，充分利用了飛行數據。