表面粗糙度對航空液壓作動器密封性能的影響

閆曉亮，杜曉瓊，常凱，李夢晨

(航空工業慶安集團有限公司 航空設備研究所， 西安 710077)

0 引 言

目前，飛機液壓系統的壓力向著高壓化方向發展，已經有越來越多的先進飛機采用35 MPa壓力體系[1]。作為單獨或者集成于電靜液作動器中的執行元件，液壓作動器一旦發生泄漏，輕則引起環境污染，降低系統傳動效率，重則影響飛機任務的執行甚至危脅飛行安全。液壓作動器在工作中會受到溫度、壓力、振動、密封材料性能及作動速度等因素的明顯影響，其密封性能受流固與熱相互耦合作用影響。

目前，國內對航空液壓往復密封的理論研究較為缺乏，沒有完善的理論指導，密封設計大多基于工程經驗和仿制國外先進密封結構。受實驗手段的限制，當前的實驗研究也無法真實描述密封機理。

隨著計算科學的飛速發展，仿真技術成為科研人員探索工程問題的重要手段，通常采用數值方法研究往復密封規律。國外，G.K.Nikas等[2-3]針對做往復運動的矩形密封圈建立了數值仿真模型，并進行了一系列數值仿真研究；M.Scaraggi等[4]將軟彈性體密封的平均流量模型進行了理論擴展，模擬實際加工表面粗糙度對密封的影響；M.Crudu等[5]將試驗和數值方法結合，考察了表面粗糙效應對做往復運動的活塞桿密封性能的影響；S.Bhaumik等[6]進一步將磨損仿真應用到表面粗糙度對往復密封的影響分析。國內，張延良等[7]、董峰[8]采用數值方法研究了組合密封滑環表面粗糙度對往復密封性能的影響；歐陽小平等[9]建立了基于混合潤滑理論的多場耦合模型，研究了典型航空高壓往復密封問題，考察了高壓、高溫及速度的影響；Xiang Chong等[10]基于平均流量模型開發出更加高效的針對往復密封的流-固耦合算法。

上述研究大多數建立的是往復密封的統計性模型，無法考察實際密封副表面粗糙形貌的影響，而為數不多的文獻采用確定性模型的研究，也無法考慮混合潤滑狀態下的密封問題。

本文針對做往復運動的液壓作動器建立組合密封的流-固耦合確定性仿真分析模型，考察密封副的表面粗糙度及使用工況參數對密封性能的影響規律，以期為密封圈的結構設計和使用提供理論指導。

1 往復密封的求解模型

由于橡膠材料具有摩擦系數大、不耐磨、抗擠出能力差的缺點，在高壓、長行程、長壽命的往復密封場合，普遍采用橡膠圈和塑料滑環組成的組合密封形式，其中橡膠圈提供初始變形的彈力，塑料滑環與軸或者塑料滑環與襯套組成滑動副，一方面可以減小摩擦，另一方面具有較好的耐磨性。塑料滑環通常由添加了增強添加劑和減摩添加劑的改性PTFE材料制成。

由于密封圈具有軸對稱性，忽略結構偏心和軸的偏斜，則可簡化為二維線接觸模型，因此可以對上述接觸副開展結構強度分析、流體力學分析，求解得到密封接觸副的壓力分布和膜厚分布，進而預測密封副的密封性能。

在對組合密封圈進行有限元強度分析時，由于密封采用O型的橡膠材料屬于超彈性材料，具有材料非線性、幾何非線性、接觸非線性的特點，可以用超彈性本構模型通過應變能密度函數來定義。本文用兩參數Mooney-Rivlin模型來定義其本構模型[11]，其表達式為

w=C10(I1-3)+C01(I2-3)

(1)

式中：w為應變能密度；C10和C01為橡膠材料常數，本文取橡膠材料的Mooney-Rivilin常數C10=1.946 1,C01=0.461 9[12]；I1和I2為Green應變不變量。

對密封系統進行流體力學求解是為了獲得密封間隙的流體壓力分布、流體膜厚分布，并在此基礎上計算泄漏率和摩擦力。密封面的潤滑油膜控制模型為雷諾方程和密封變形模型，數值求解方法有逆解法、直接迭代法和復合直接迭代法等。

由于密封間隙往往是沿圓周方向對稱的，因此忽略沿圓周方向上參數的變化，將三維密封問題簡化為二維密封問題，且本文分析的活塞桿密封為二維穩態問題，其流體控制方程為

(2)

式中：ve為平均速度，ve=(v1+v2)/2；h、η、ρ均為x的函數，邊界條件可采用雷諾邊界條件。

在任意點x處的油膜厚度為

h(x)=hc+S(x)+σ(x)+δ(x)

(3)

式中：hc為沒有變形時的中心膜厚；S(x)為由于表面幾何尺寸變化引起的油膜厚度變化；σ(x)為由于表面粗糙形貌引起的油膜厚度變化；δ(x)為由于壓力分布在各點產生的彈性變形。

假設粗糙表面處在靜止表面，且服從正弦分布，則可對表面形貌進行確定性的描述和分析，其二維正弦粗糙表面的表達式為

(4)

式中：As為正弦波的幅值；ωx為x方向的波長；xs為正弦波表面中心的位置。

采用式(4)描述正弦粗糙表面，來考察正弦粗糙表面形貌對往復密封性能的影響。

表面彈性變形可通過Boussinesq積分式來計算：

(5)

式中：p(x)為流體壓力；psc(x)為靜態接觸壓力；s1，s2分別為載荷的起點和終點坐標；E′為等效彈性模量。

當發生粗糙接觸時，油膜厚度變成0，傳統的Reynolds方程變成如下特殊形式[13]：

(6)

式中：εh為用來判斷是否關閉壓力流動項的預設值，本文選取εh值為10 nm。

式(6)為式(2)的特殊形式，在流體潤滑區和粗糙接觸區的邊界，可自動滿足壓力連續條件。由此在一個迭代循環中可以同時求解流體壓力和粗糙接觸壓力。

粘-壓關系式采用Roelands粘壓公式

(7)

式中：α為潤滑油的黏-壓系數，Pa-1；η0為液壓油的環境黏度，Pa·s。

密-壓關系采用Dowson-Higginson公式來計算：

(8)

式中：ρ0為液壓油的環境密度，kg/m3。

2 往復密封的流固耦合數值求解方法

數值迭代求解過程如圖1所示。在求解往復密封的潤滑問題時，首先根據給定的密封幾何尺寸、材料參數和安裝參數，借助有限元軟件計算密封接觸副的靜態接觸壓力和結構變形，然后連同潤滑油參數、工況參數、初始油膜厚度作為流固耦合求解的輸入條件開展耦合求解。每次在修正完流體壓力后，根據彈性變形方程更新膜厚，并計算新的潤滑油黏度和密度。當壓力求解收斂后，再判斷膜厚是否收斂，如不收斂，則修正油膜厚度。為了加快計算速度，采用基于離散卷積和快速傅里葉變換法的彈性變形計算法[14]。

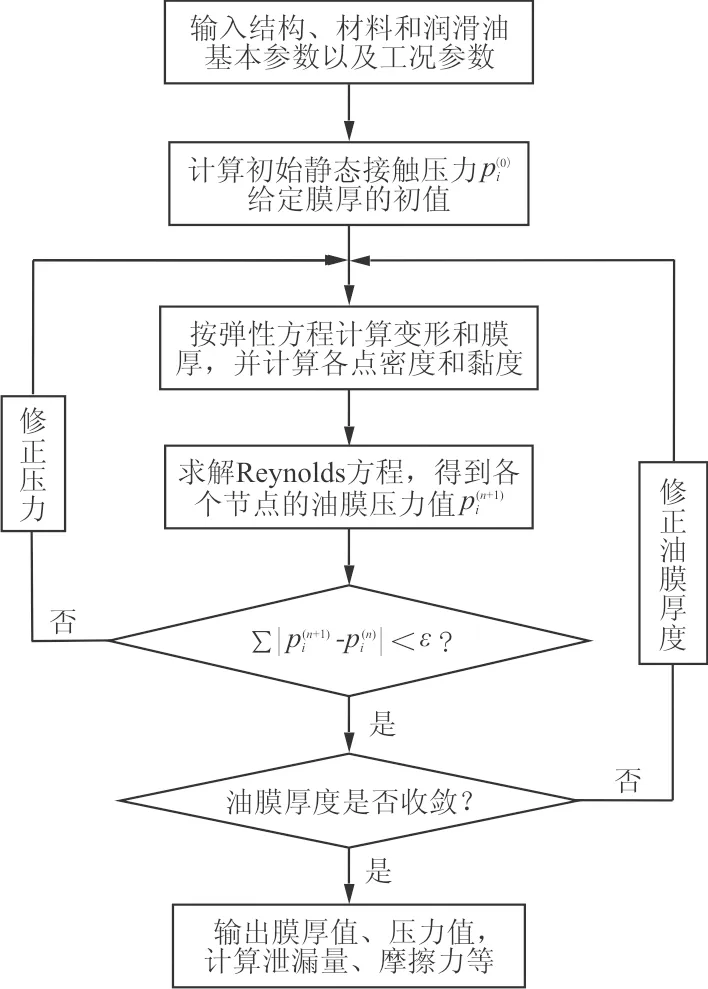
圖1 數值迭代求解流程圖

3 計算結果及影響分析

以Greene Tweed公司的ACGT型密封圈為例進行計算。ACGT型密封圈由4部分組成，左、右兩側為擋圈結構，截面呈T型結構的部分由橡膠材料制成，起減摩和密封作用的滑環由改性PTFE材料制成。該型密封圈的優點是呈T型截面的彈性體能夠很好地避免往復運動中的扭轉，滑環做的很薄能夠及時對磨損進行補償，徑向尺寸小、密封性能好，在航空液壓作動器上得到了廣泛的應用。密封圈安裝后的有限元網格模型如圖2所示，該密封圈內徑為46.83 mm。由于結構和所受工況的對稱性，對ACGT型密封結構進行有限元分析時，將其簡化成二維軸對稱模型，其中y軸為對稱軸。

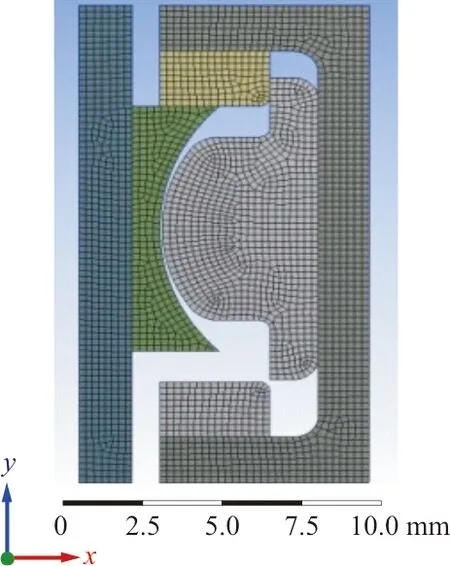
圖2 ACGT型密封圈的有限元網格模型

密封壓力為28 MPa，安裝后由有限元軟件求解得到的ACGT型密封圈的T型橡膠密封圈和滑環的應力分布云圖為圖3所示，可以看出：在油壓作用下密封圈所受的最大接觸壓力靠近出口側。

(a) T型密封圈 (b) 滑環

在得到密封圈的接觸壓應力后，將其作為初始值開展雙向流固耦合數值分析，用以得到密封區域的油膜厚度和油膜壓力分布，并可在此基礎上預測泄漏量和摩擦力。

3.1 正弦粗糙表面波長和幅值對油膜厚度和壓力的影響

在算例中，共同的輸入參數包括：軸的彈性模量E=210 GPa，泊松比ν=0.3，密封壓力pseal=28 MPa，出口壓力pout=0.1 MPa，液壓油的環境密度ρ0=800 kg/m3。

活塞桿運動速度v=0.1 m/s，潤滑油動力黏度η0=0.01 Pa·s，正弦粗糙幅值Ra=0.1 μm，正弦粗糙表面的波長ω分別取為10、40、160、320、640 μm時，對應的密封區域油膜壓力分布和油膜厚度分布及壓力和膜厚的局部放大圖如圖4所示。

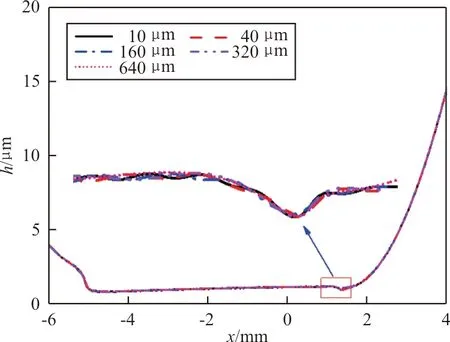
(a) 膜厚分布

從圖4(a)可以看出：雖然油膜分布適應表面形貌發生變化，但是在此工況下，正弦粗糙表面的波長變化對密封區域油膜厚度的影響很小。從圖4(b)可以看出：隨著正弦波長增大，壓力的波動減弱，這是與表面形貌變化相一致的；但是正弦波長增大引起油膜壓力幅值增大，且波長越大對應的油膜壓力的幅值越大。

活塞運動速度v=0.1 m/s，潤滑油動力黏度η0=0.01 Pa·s，正弦粗糙表面的波長ω分別為10、40、160、320、640 μm，正弦粗糙幅值增大為Ra=0.6 μm時，對應的密封區域油膜壓力分布和油膜厚度分布及局部放大圖如圖5所示。

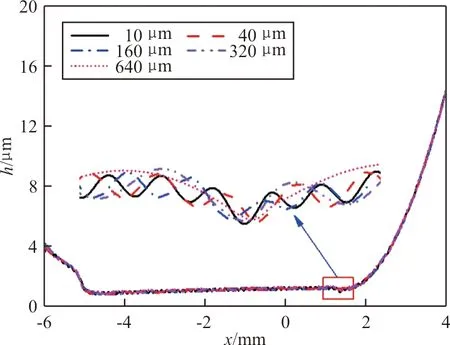
(a) 膜厚分布

從圖4～圖5可以看出：正弦粗糙表面的幅值增大，導致油膜厚度和油膜壓力的波動幅值增大。從圖5(a)可以看出：存在顯著的油膜波動，油膜波動與正弦表面的波形是適應的，波長越小波動越劇烈。從圖5(b)可以看出：即使沒有局部放大圖，也可以觀察到明顯的由于表面粗糙形貌引起的壓力波動，且比圖4(b)中Ra=0.1 μm時的壓力波動要顯著的多。因此得出：正弦幅值和波長越大，油膜壓力波動的幅值越大。

3.2 正弦粗糙表面波長對密封區域最小油膜厚度的影響

三個不同運動速度v分別取0.04、0.1、0.2 m/s，以及三個不同正弦粗糙表面幅值(Ra分別為0.1、0.3、0.6 μm)對應的最小油膜厚度如圖6所示，可以看出：總體來說，密封間隙最小膜厚隨正弦粗糙表面波長變化而幅度變化較小，最小膜厚沒有隨著正弦粗糙表面波長變化呈現單調變化或者出現顯著的趨勢性變化。這說明正弦粗糙表面波長ωx對密封間隙最小膜厚的影響作用較弱。

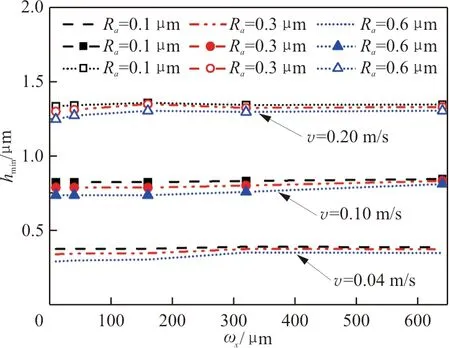
圖6 正弦波長變化對最小膜厚的影響

正弦粗糙表面波長變化對摩擦系數的影響如圖7所示，可以看出：隨著正弦粗糙表面波長的增大，摩擦系數呈現單調減小的趨勢，且正弦粗糙表面幅值大(如Ra=0.8 μm)時對應的摩擦系數受波長變化的影響要更大一些；活塞運動速度增大時，波長對摩擦系數的影響作用減弱。

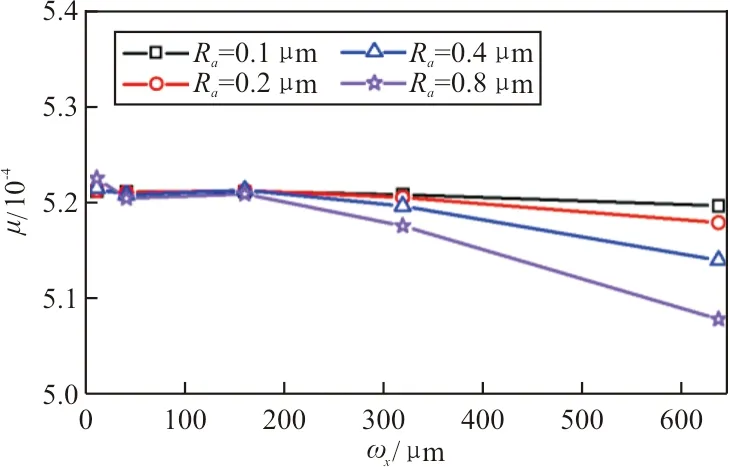
(a) 速度v=0.04 m/s

不同正弦粗糙表面波長下，摩擦系數隨粗糙表面幅值的變化如圖8所示，可以看出：正弦粗糙表面幅值增大有利于摩擦系數的減小；波長增大有利于減小摩擦系數，且速度增大時正弦粗糙表面幅值變化對摩擦系數的影響作用減弱。

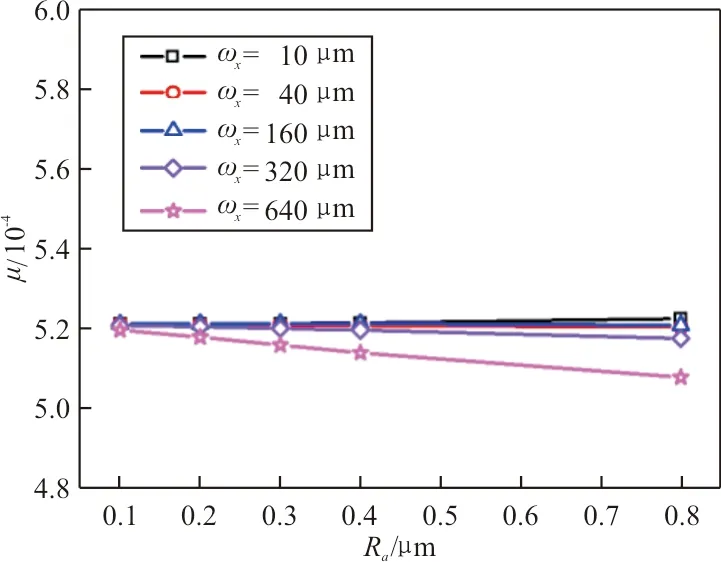
(a) 速度v=0.04 m/s

3.3 活塞運動速度和液壓油黏度變化對密封間隙最小油膜厚度、摩擦系數和泄漏量的影響

在分析運動速度的影響時，取三個不同的液壓油黏度進行計算。

正弦粗糙幅值Ra=0.2 μm，波長ωx=160 μm時，三個不同液壓油黏度η0下，活塞運動速度v對密封間隙最小膜厚hmin、泄漏量Q和摩擦系數μ的影響如圖9所示，可以看出：密封間隙最小膜厚hmin、泄漏量Q均隨著活塞運動速度v增大而單調增大，這是由于活塞運動速度v增大，增強了對油液的卷吸效應，有利于油膜厚度的增大；全膜潤滑的摩擦系數也相應增大，摩擦系數隨著運動速度v增大的原因主要是剪切效應增大導致的。

(a) 最小膜厚hmin

正弦粗糙幅值Ra=0.2 μm，波長ωx=160 μm時，三個不同活塞運動速度v下，液壓油黏度η0對密封間隙最小膜厚hmin、摩擦系數μ和泄漏量Q的影響如圖10所示，可以看出：液壓油黏度η0對密封間隙最小膜厚hmin、摩擦系數μ和泄漏量Q的影響作用與運動速度v的影響作用類似，液壓油黏度η0增大引起最小膜厚hmin、摩擦系數μ和泄漏量Q的單調增大。

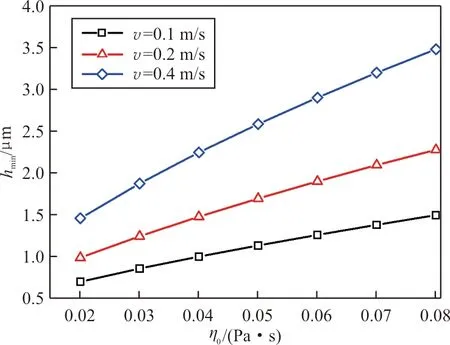
(a) 最小膜厚hmin

對于表面不可避免地存在粗糙度的密封圈來說，增大液壓油的黏度或活塞桿的運動速度，有利于增大密封間隙油膜厚度，對密封圈的潤滑是有利的；但同時會導致泄漏量和流體潤滑摩擦系數的增大。液壓油黏度的主要影響因素是油液本身的品質和環境溫度，對于特定的航空潤滑油來說，想要達到低泄漏率和長壽命，采用的措施是控制作動器的運行溫度在合理范圍內。

4 結 論

(1) 正弦粗糙表面的幅值和波長增大，引起油膜厚度和油膜壓力的波動幅值增大，但摩擦系數減小。

(2) 正弦粗糙表面的幅值增大，引起密封間隙最小膜厚的減小，而波長對最小膜厚的影響作用不大。

(3) 隨著速度增大，正弦粗糙表面的幅值和波長變化對摩擦系數的影響作用減弱。

(4) 液壓油黏度和活塞桿運動速度的增大有利于密封圈的潤滑，但同時會導致泄漏量和流體潤滑摩擦系數的增大，在實際使用時需要綜合考慮二者對密封性能和長期使用壽命的影響。