基于MATLAB 的6R 焊接機器人運動學的仿真研究

熊思淇，陳緒兵，張 聰，戴耀南

武漢工程大學機電工程學院，武漢 430205

自焊接機器人問世以來，在制造業的多個領域當中應用越來越廣泛，包括汽車工業、航天航空以及船舶等行業。經過50 多年的發展，焊接機器人的焊接質量越來越穩定，對于改善勞動條件和提高生產效率起到了重要的作用，尤其是在焊接領域，已經逐漸取代了原始的人工焊接，從提高和優化焊接質量和效率的角度出發，提出多機器人協調焊接的方法［1-2］。在研究多機器人的協調焊接之前，首先需要對單個焊接機器人進行運動學問題研究。其中，機器人的運動學建模是通過機器人的正向運動學分析來理解角度參數轉換成坐標的具體過程；通過機器人的逆向運動學來理解位置坐標是如何轉化成角度參數的，同時在這個過程中還需要對奇異解進行分析判斷，選擇正確合理的解；按照作業要求明確機器人的軌跡規劃，掌握其末端運動狀態（末端點運動軌跡）。大部分專家學者在進行機器人運動仿真研究的時候都選擇應用MATLAB 環境中的Robotics Toolbox［3-4］并借助于仿真參數進行機器人研究，包括其正、逆運動學和軌跡規劃等內容。譬如，左富勇等［5］對四自由度的SCARA 機器人進行了運動學仿真，得到了該機器人平滑的運動軌跡，但是對六自由度的機器人適用性不足；王智興［6］、干敏耀［7］分別對Standford和Puma 機器人進行仿真研究，但都只是針對特定型號的機器人進行研究；陸家皓等［8］在研究當中，以6R 關節型ER3A-C60 機器人為對象，對其相關參數的合理性進行了仿真研究和驗證，不足之處在于沒有進行正、逆運動學仿真驗證，導致無法獲得完整的仿真結果；李瑾等［9］直接調用工具箱中的逆解函數來對Puma250 機器人求逆解，由于逆解函數是運用迭代法來求解逆運動，存在著局限性，導致出現了漏解的情況，因此不能對逆運動學進行逆解驗證。針對上述問題，本研究以應用較為廣泛的ABBIRB1600 型號機器人為研究對象，針對其正逆運動學進行了研究和分析，借助于標準Denavit-Hartenberg（D-H）建模法，構建機器人模型以及正逆運動學方程，并通過調用工具箱正逆解函數的方式對正逆運動學結果進行求解，然后分別比對計算值和實際實驗值，對本研究構建的運動學模型和正逆運算結果的正確性進行科學的驗證，為今后研究焊接機器人軌跡提供了必不可少的理論基礎和運動學模型。

1 機器人運動學分析

機器人運動學指的是，對機器人的每個關節點和大地坐標系之間的相對位姿進行全面的分析，最終獲取其末端執行器與大地坐標系相對應的位姿、速度和加速度情況。其整體分析過程可以分成兩個不同的類型，分別是正、逆運動學，具體分析過程如圖1 所示。

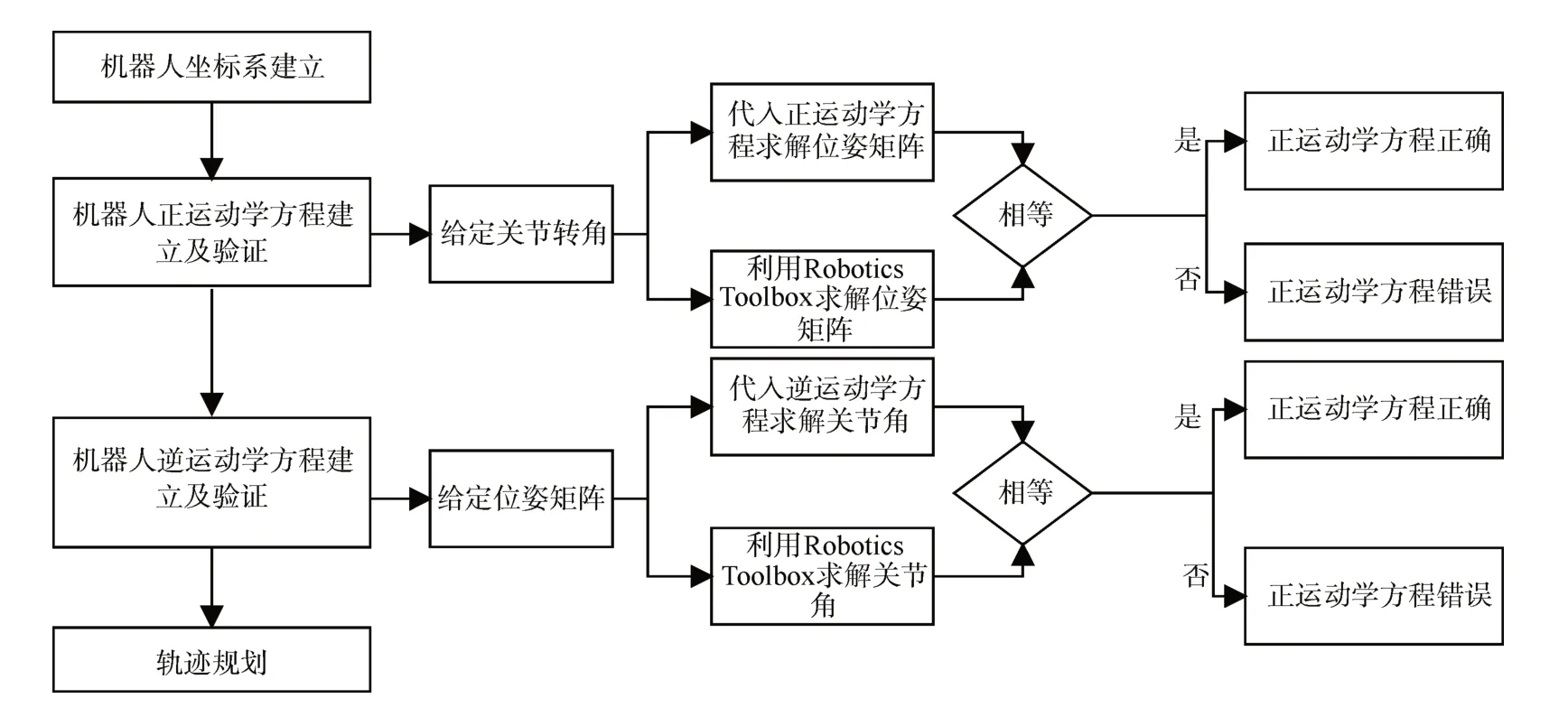
圖1 運動學分析流程圖Fig.1 Flowchart of kinematics analysis

1.1 機器人基本結構

ABBIRB1600 型工業機器人是一款6R 關節串聯機器人，其仿真模型如圖2 所示，它的主體組成包括基座、腰部、大小臂以及手腕等部分，各相鄰關節之間都是通過轉動關節來聯接，在焊接、碼垛等領域均有廣泛的應用。

根據圖3 中機器人的結構構型以及相關尺寸參數，通過標準D-H 參數建模方法，建立機器人坐標系，其建模步驟如下：

1）繞zi-1軸旋轉θi，使得xi-1與xi互相平行，記為旋轉矩陣R；

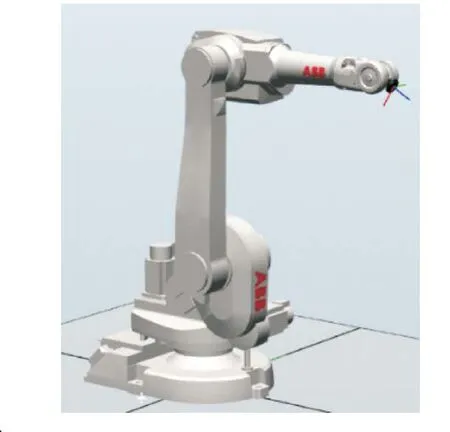
圖2 Robotstudio 中ABBIRB1600 仿真模型圖Fig.2 Diagram of ABBIRB1600 simulation model in Robotstudio

圖3 ABBIRB1600 結構構型和尺寸參數（單位：mm）Fig.3 Structural configuration and dimension parameters of ABBIRB1600（Unit：mm）

2）沿zi-1軸 平移di距離，使得xi-1與xi共線；

3）沿xi軸平移ai距離，使得xi-1與xi的原點重合，記為平移矩陣T；

4）將zi-1軸繞xi軸旋轉αi，使得zi-1軸與zi對準。

構建的機器人坐標系如圖4 所示，獲得的連桿參數以及關節變量如表1 所示，其中ai和di分別表示相鄰關節間的連桿長度和連桿偏移量，αi代表相連坐標系間的扭轉角度，θi代表關節旋轉角度制。在各參數之中，只有θi為可變參數，其余參數均為定值。

圖4 ABBIRB1600 機器人坐標系Fig.4 ABBIRB1600 robot coordinate system

表1 ABBIRB1600-10/1.45 機器人D-H 參數Tab.1 ABBIRB1600-10/1.45 Robot D-H parameter

1.2 機器人正運動學

已知機械臂每個關節的角度參數之后，可以根據關節和末端執行器間的坐標變化關系，對末端執行器的位置以及姿態進行正確的求解。相鄰坐標系與能夠通過齊次變換矩陣進行表述［10］：

對應于機器人連桿坐標系的描述，可以得到機器人相鄰兩個關節之間的齊次變換矩陣分別為［11-13］：

ABBIRB1600 機器人末端坐標系{ }6 與基坐標系{ }0 之間的變換矩陣為且有：

將機器人的每個坐標轉換矩陣帶入式（2），即可得到機器人正向運動學方程：

為 簡 化 公 式，使 用si代 表 sinθi，ci代 表cosθi，s23代表代表故式（3）化簡得到：

1.3 機器人逆運動學

機器人逆運動學，就是通過機器人末端笛卡爾空間來求解機器人關節空間，即在知道末端位置和姿態的情況下，求出各個關節的旋轉角度。求逆解具有多種不同的方法，然而在實際應用當中，一般使用兩種封閉解法來獲取有效封閉解：一是代數解法，另一種是幾何解法。幾何解法需要將D-H 參數表的空間幾何參數轉換到平面幾何參數上去，并求解；代數解法是運用變換矩陣就得到求解的三角函數方程式。相比于幾何解法，雖然代數解法過程復雜，但能夠得到全部的解，且所求角度均處在適當的象限里，故使用代數解法。在機器人運動方程（3）的兩端分別乘上對應的逆矩陣，分離變量，并根據各個關節變量的值來求解矩陣的相等元素［14］。

1）計算θ1

令式（4）兩端（3，3）和（3，4）相等，得：

由于機械臂的旋轉對應的不同的姿態，則θ1會有兩組解：

2）計算θ3

令式（4）兩端（2，3）和（2，4）相等，得：

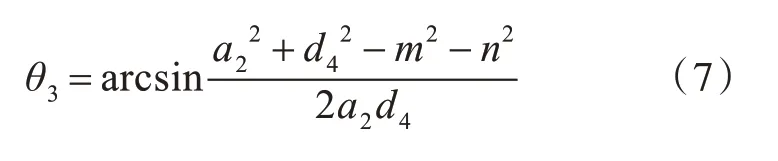
其中，

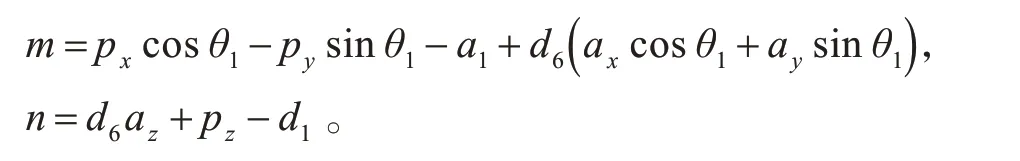
由于m中含有關于θ1的三角函數，因此θ3的大小與θ1的取值有關，并且θ3也會因為機械臂的旋轉對應著不同的姿態，所以θ3存在著兩組解。

3）計算θ2

根據步驟2 可推出θ23，其中θ2的值與θ1、θ3的取值相關，θ1的值會產生兩個θ3的值，每一組θ1和θ3對應產生一個θ2的值，所以可以通過式（9）得到四組θ2的解：

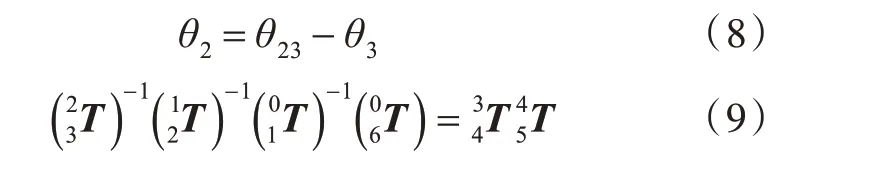
4）計算θ5

令式（9）兩端（3，3）相等，得：5）計算θ4

令式（9）兩端（1，3）和（2，3）相等，得：

6）計算θ6

令式（9）兩端（3，1）和（3，2）相等，得：

至此，關節角θ1～θ6已經通過計算全部求出，完成了ABBIRB1600 焊接機器人的逆解求取過程。

通過圖5 逆運動學求解過程可以看出θ1、θ2、θ3存在著多組逆解，并且相互組合可以產生八組逆解。多個逆解的存在讓機器人的末端位姿可以有多種姿態選擇，但在實際運動過程中，需要考慮整個運動過程以及機械參數的約束，因此部分逆解可能處于機械臂不可達空間內，或者某些位姿不符合具體的任務要求，所以對得到的逆解必須進行驗證。

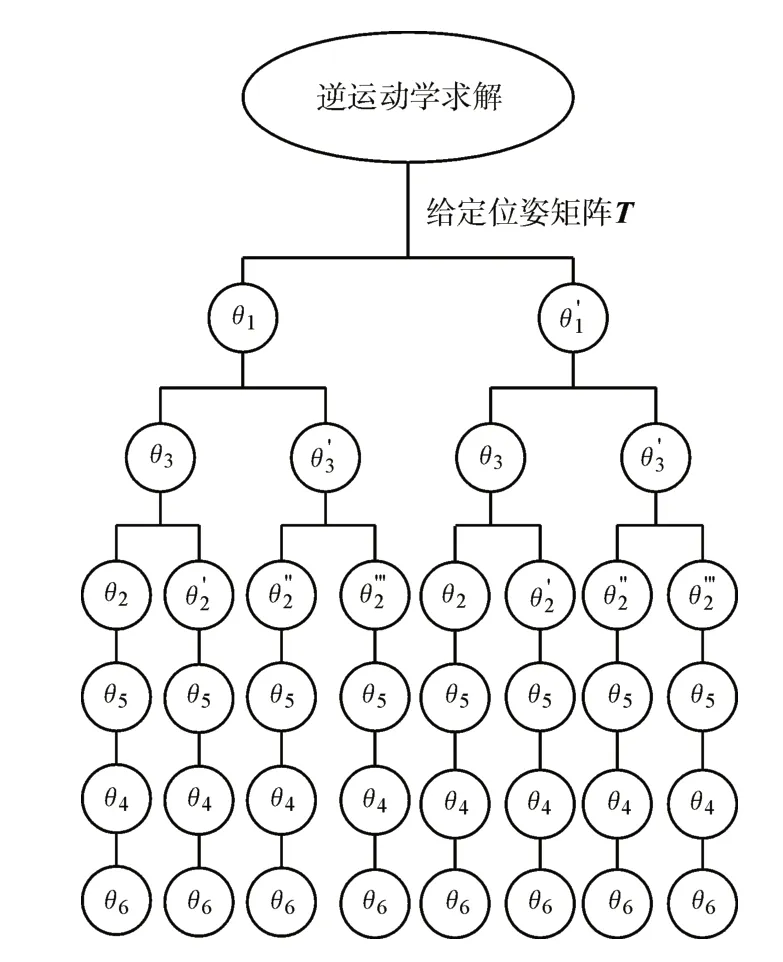
圖5 逆運動學求解過程Fig.5 Inverse kinematics solution

2 機器人運動學模型仿真

2.1 建立運動學模型

在MATLAB 軟件當中，有專門服務于工業機器人的工具箱Robotics Toolbox，它能夠提供多種機器人所需的運動學函數。可以依據表2 的數據，利用Robotics Toolbox 工具箱完成機器人建模［15-16］，獲取到的初始位姿如圖6 所示。

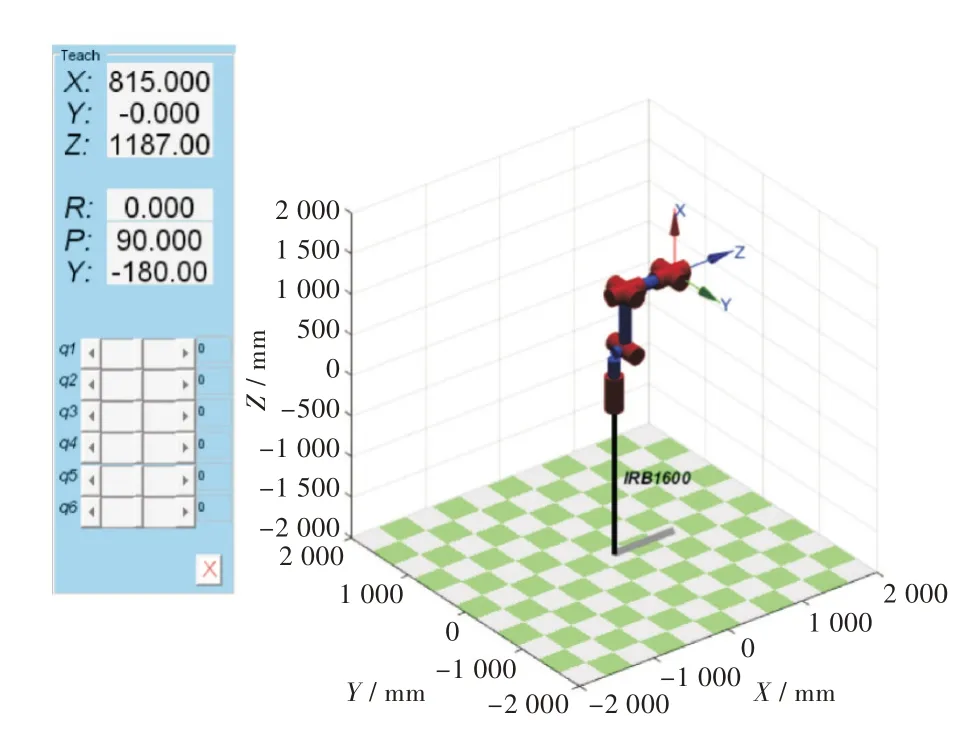
圖6 MATLAB 中ABBIRB1600 的初始位姿Fig.6 Initial pose of ABBIRB1600 in MATLAB

2.2 正運動學驗證

按照隨機的方式挑選一組關節變量，將其應用于正運動學方程求解正確性的驗證；使用公式（3）所示的正運動學方程當作計算值，選擇末端執行器位姿當作真值。 隨機選取關節變量q1=[0 0 0 0 0 0]，將計算值與真值進行數據對比。

通過1.2 節機器人正運動學方程，帶入q1的值，求得末端位姿矩陣T1：

使用Robotics Toolbox 求解正運動學，可以獲取末端位姿矩陣G：

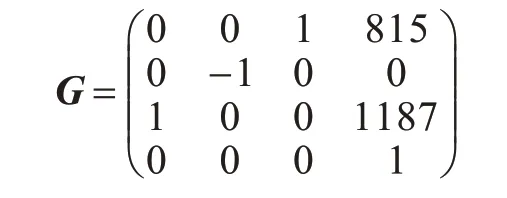
對比計算值T1與真值G，驗證了機器人正運動學方程與運動學模型的正確性。

2.3 逆運動學驗證

根據Robotics Toolbox 工具箱可以對關節變量為q2=[45 30 60 90 15 22.5]的機器人進行求解，可得其末端位姿矩陣T2：

將求解得到的T2代入（1.3）節中的逆運動學公式可以計算出機器人多組運動學逆解Q2=[θ1θ2θ3θ4θ5θ6]。通 過MATLAB 編 寫 計 算 程序對逆解進行計算，如表2 所示。

根據表2 可知，每個位姿都能夠得到八組解，然而在實際的應用中，在機械機構約束和不同桿件運動干涉的影響下，機器人能夠真正到達的關節角度只有其中的一部分。將數據進行比對之后發現，表2 當中第4 組的取值等同于q2，由此可以對逆運動學的正確性進行有效的驗證。

2.4 軌跡規劃與仿真

軌跡規劃方法是對機器人在運動狀態下的位移、角速度及角加速度進行規劃，得到其運動曲線，并觀察機器人具體的運動狀態［17-18］。本文選擇的是關節空間軌跡規劃法，在空間中選擇任意兩點，調用工具箱在關節空間內對機器人進行軌跡規劃。設關節空間中初始點對應的關節轉角為末端點對應的關節轉角為得到的運動軌跡如圖7所示。

本研究需要同時針對6 個關節進行研究，分別針對其角位移、角速度和角加速度進行規劃。為了對所有關節的運動曲線進行清晰準確的觀察，本文使用MATLAB 繪制了所有關節的仿真曲線，如圖8 所示。

表2 位姿T 的運動學逆解Tab.2 Inverse kinematics of pose T （°）

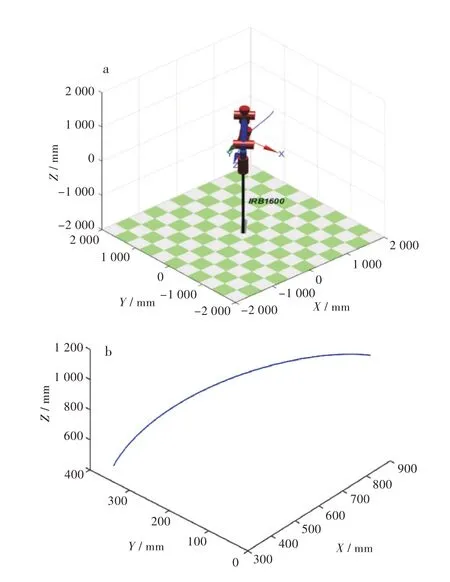
圖7 ABBIRB1600 初始點到末端點的運動過程：（a）運動軌跡，（b）末端三維軌跡Fig.7 Motion process of ABBIRB1600 from initial point to end point：（a）motion trajectory，（b）three-dimensional trajectory map of end

通過觀察圖8 可以得知，機器人在整體運動過程中，6 個關節都能夠保持平穩的運動狀態進行正常工作。所有關節的角位移曲線都呈現為光滑無突變，由此可知，每個桿件間都沒有出現錯位沖突；角速度和加速度的曲線都呈現為連續的狀態，且變化緩和，由此可知，機械臂在工作中能夠保持平穩運行，產生的振動幅度較小，對運動學模型連桿參數設計的合理性以及運動學方程的正確性進行了有效的驗證，也說明了機器人能夠順利到達預設位置。

圖8 ABBIRB1600 各關節仿真曲線：（a）角位移，（b）角速度，（c）角加速度Fig.8 Simulation curves of each joint of ABBIRB1600：（a）angular displacement，（b）angular velocity，（c）angular acceleration

3 結 論

在本文的研究中，以ABBIRB1600 型號機器人作為研究對象，從運動學的角度分析了6R 焊接機器人，并對其進行了軌跡規劃的仿真，根據仿真結果得出結論如下：

1）基于標準D-H 法，建立了ABBIRB1600 機器人的D-H 坐標系，在此基礎上分別求出相鄰連桿間的位姿變換矩陣以及機器人的正逆運動學方程。借助于運動學方程的求解過程，分別從正、逆運動學方面對機器人進行了科學的分析，然后在MATLAB 環境當中完成程序編寫，并從理論的層面得出了8 組位姿逆解。將計算值和實際實驗值進行了比對，完成了正逆運動學方程正確性的驗證工作。

2）借助MATLAB 中的Robotics Toolbox 工具箱完成相關程序的編寫，然后在關節空間內，進行了機器人運動軌跡的仿真，分別獲取每個關節的角位移、角速度以及角加速度和時間變化之間產生的平滑運動曲線，驗證了機器人參數的合理性。