以形助數 以數解形
?董苗紅

《數學課程標準》中明確指出:“通過義務教育階段的數學學習,學生能夠獲得適應未來社會生活和進一步發展所必需的重要數學知識以及基本的數學思想方法和必要的應用技能。”數學思想有許多,數形結合思想就是其中一種重要的思想。數形結合就是通過數與形的相互轉化、相輔相成來解決數學問題的一種思想方法。它既是一個重要的數學思想,又是一種常用的數學方法。在教學中滲透數形結合的思想,可把抽象的數學概念直觀化,幫助學生形成概念;可使計算中的算式形象化,幫助學生在理解算理的基礎上掌握算法;可將復雜問題簡單化,在解決問題的過程中,提高學生的思維能力和數學素養。
我國著名數學家華羅庚曾說過:“數形結合百般好,隔裂分家萬事非。”“數”與“形”反映了事物兩個方面的屬性。數形結合,主要指的是數與形之間的一一對應關系。數形結合就是把抽象的數學語言、數量關系與直觀的幾何圖形、位置關系結合起來,通過“以形助數”或“以數解形”即通過抽象思維與形象思維的結合,可以使復雜問題簡單化,抽象問題具體化。本人談談在教學中的點滴體會:
一、概念教學中的數形結合
建構主義認為學生學習活動的本質是:學習并非對于教師所授予的知識的被動接受,而是學習者以自身已有的知識和經驗為基礎的主動建構過程。數學意義所指的“意義”是人們一致公認的事物的性質、規律以及事物之間的內在聯系,是比較抽象的概念。而“數形結合”能使比較抽象的概念轉化為清晰、具體的事物,學生容易掌握和理解。
例如:二年級上冊《乘法的初步認識》中通過游樂場主題圖來引入乘法,為了讓學生理解乘法的意義,教材提供了大量同數連加的現實情境,如坐小飛機、小火車和過山車的同學,每束個數相同的氣球,每串數量相同的鑰匙以及每份數量相同的胡蘿卜、香蕉等等,為學生提供豐富而生動的直觀圖像,然后讓學生對照圖形寫同數連加算式,再引導學生用 “幾個幾”的方式來表達同數連加的具體情境,最后將同數連加的算式改寫成乘法算式。通過具體情境的圖形與乘法算式的結合,使學生不僅理解了乘法的意義,而且懂得了乘法是同數相加的簡便運算。
從學生的思維活動過程來看:在這個學習過程中,學生經歷了由具體到抽象的思維過程,也就是由直觀的同數連加的具體情境圖,抽象成連加算式,再抽象成乘法算式,經歷了由一般到特殊的思維過程。
二、計算教學中的數形結合
小學數學內容中,有相當部分的內容是計算問題,計算教學要引導學生理解算理。算理就是計算方法的道理,學生不明白道理又怎么能更好的掌握計算方法?在教學時,教師應以清晰的理論指導學生理解算理,在理解算理的基礎上掌握計算方法,正所謂“知其然,知其所以然。數形結合,是幫助學生正確理解算理的一種很好的方式。如,在教學“分數乘分數”時,出示例題:李伯伯家有一塊 公頃的地。種土豆的面積占這塊地的 ,種土豆的面積是多少公頃?要理解分數乘分數的算理,其根本在于對分數意義的理解。讓學生先明確 公頃就是1公頃的 ,求種土豆的面積就是求 公頃的 ,是以 公頃為單位“1”,把它平均分成5份,取其中的1份。可以讓學生畫畫圖,用圖示幫助理解算理。
把算式形象化,學生看到算式就聯想到圖形,看到圖形能聯想到算式,更加有效地理解了分數乘分數的算理。
以上的例子就是將抽象數學語言與直觀圖形結合起來,使抽象思維與形象思維結合起來,通過“數”與“形”之間的對應和轉換來理解算式的意義。
三、解決問題教學中的數形結合
小學生在學數學的過程中,往往會單維度地思考問題,這其實就是受他們空間想象能力制約的影響。兒童在觀察的過程中,只觀察到事物的表面現象,卻不能透過現象,找出事物的本質。教師應指導他們逐漸懂得看問題應該從什么角度看,找出問題內在的規律,逐步形成由淺入深,利用數形結合的思想,將復雜問題簡單化。
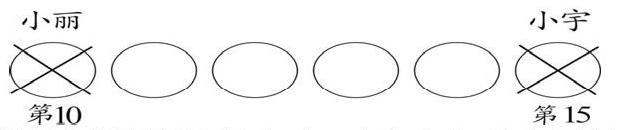
有些數學問題對于學生而言比較復雜的原因并非解答過程比較繁瑣,而是沒有方法。因此,把復雜的問題轉化為簡單的問題,要尋求一些技巧和捷徑,運用幾何直觀也不失為一種上策。如:人教版一上P79例題6,小麗排第10,小宇排第15,小麗和小宇之間有幾人?對于一年級的孩子,他們還沒有什么解題經驗,他們容易憑直覺直接運用這兩數計算:15-10=5(人),個別學生扳起手指逐一數出之間應有4人。這時教師可引導學生畫一畫,如圖所示,
更加直觀的把題目呈現出來,同時也看出了結果。啟迪孩子的思維,讓孩子直觀感受人數與間隔數的關系,讓孩子明白有些題目通過畫圖可以畫出答案,畫圖能幫助解決問題。在以上的解決問題的過程中,滲透了數形結合的思想。
四、運算定律的教學中的數形結合
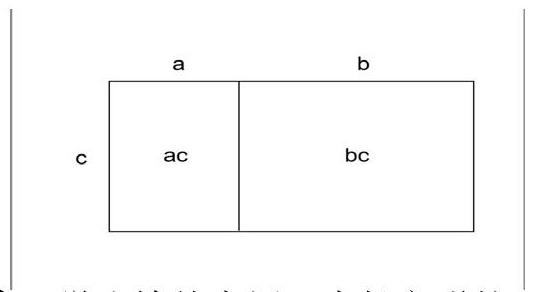
兒童的認識規律,一般來說是從直接感知到表象,再到形成科學概念的過程。表象介于感知和形成科學概念之間,抓住這中間環節,發展學生的空間觀念,培養初步的邏輯思維能力,具有十分重要意義。例如在學生學習了乘法分配律后,教師可以引導學生用圖形的面積計算來解釋乘法分配律:(a+b)×c=ac+bc。
數形一結合,學生恍然大悟:大長方形的面積是長(a+b)乘寬(c),即(a+b)×c;大長方形的面積也可以看作兩個小長方形的面積之和,即ac+bc。由此可以得出:(a+b)×c=ac+bc。
從這里不難看出:“數”、“形”互譯的過程,也是學生的形象思維與抽象思維協同運用、互相促進、共同發展的過程。由于抽象思維有形象思維作支持,從而使運算定律變得形象生動。
綜上所述,在小學數學教學中,學生懂得“數形結合”的數學思想方法后,對于小學數學知識的理解性記憶是非常有益的。在數學教學活動中,通過數與形的結合,能夠有的放矢地幫助學生多角度、多層次地思考問題,可以養成多向性思維的好習慣。因此,教學中要對學生加強滲透“數形結合”思想,培養學生運用“數形結合”的意識。

